下载文档原格式
什么是经济订货批量模型?经济订货批量模型公式什么是经济订货批量模型?经济订货批量模型公式经济订货批量模型(Economic Order Quantity, EOQ)：又称整批间隔进货模型EOQ模型，是目前大多数企业最常采用的货物定购方式.该模型适用于整批间隔进货、不允许缺货的存储问题，即某种物资单位时间的需求量为常D，存储量以单位时间消耗数量D的速度逐渐下降，经过时间T后，存储量下降到零，此时开始定货并随即到货，库存量由零上升为最高库存量Q，然后开始下—个存储周期，形成多周期存储模型。
经济订货批量模型最早由于1915年提出的,该模型有如下假设:(1)需求率已知,为常量.年需求量以D表示,单位时间需求率以d表示.(2)一次订货量无最大最小限制.(3)采购,运输均无价格折扣.(4)订货提前期已知,为常量.(5)订货费与订货批量无关.(6)维持库存费是库存量的线性函数.(7)补充率为无限大,全部订货一次交付.(8)不允许缺货.(9)采用固定量系统.EOQ 经济订货批量EOQ的概念，公式，案例分析，公式推导证明，适用情况,缺陷1.经济订货批量EOQ 的概念经济订货批量是固定订货批量模型的一种，可以用来确定企业一次订货的数量。
当企业按照经济订货批量来订货时，可实现订货成本和储存成本之和最小化。
2.公式为Q* = SQRT(2*DS/C)Q*-- 经济订货批量D -- 商品年需求量S -- 每次订货成本C --单位商品年保管费用3.案例分析仓储的管理很类似于生活中自来水水塔现象：水塔是个蓄水池，不停的漏水，快漏完的时候，就要迅速加水至满，保持平衡。
对于某医药配送企业仓库管理，可以看作它是集中大量采购，然后慢慢销售；快完的时候，在集中大量采购，如此循环；为了便于建模，我们把上面问题看的再理想化些：水塔的水是均匀漏的，加水时是瞬间加满的；该医药配送企业的某种药品的销售也是均匀的已一个固定的速度出库，采购的动作也是瞬间完成的；要解决的问题描述(水塔现象的对照)1.水塔负责的小区居民，一年有1000吨的用水量，每吨水的价格1元，每吨水的保管费用平均为一年元，每次水泵抽水至水塔需要费用2元；那么我们根据这些数据，想到的结论是什么呢？那就是这个水塔要建立多大，每隔多长时间送一次水？一年的总费用是多少？2 .该医药配送企业某种药品一年销售10000箱，每箱进价100元，每箱货的保管费用平均为一年5元，每次供应商送货的手续费170元；根据这个数据，我们想知道：每次采购多少箱？多长时间采购一次？一年的总费用是多少？年费用的计算该医药配送企业一年的总费用计算公式=商品的总进价+全年的保管费+全年订货手续费=每箱进价*销售总箱数+(每箱年保管费/2*销售总箱数)/订货次数+每次订货手续费*订货次数这里有人概念容易误解，就是全年的保管费的计算；很容易让人感觉:全年的保管费=每箱年保管费*销售总箱数;下面我举一个最简单的例子否定上面想法：比如仓库月初进了30箱货，每箱每天的保管费用为1元，那么到月底的时候保管总费用是不是(1元/箱.天)*30箱*30天=900元呢？实际上你要考虑到箱子在均匀出库。
经济订货批量扩展模型公式摘要：I.引言- 介绍经济订货批量（EOQ）模型- 指出EOQ 模型的局限性- 引入经济订货批量扩展模型（EOQX）II.EOQX 模型假设- 需求波动的泊松分布假设- 订货成本和库存成本的假设III.EOQX 模型公式- 公式推导- 公式解释IV.EOQX 模型应用- 计算经济订货批量- 考虑需求波动的影响V.结论- EOQX 模型的优点- EOQX 模型在库存管理中的应用正文：I.引言经济订货批量（EOQ）模型是库存管理的基本模型，用于计算一次订货的最佳数量。
EOQ 模型假设需求是常量，订货成本和库存成本与订货数量和库存数量成正比。
然而，在实际应用中，需求可能会有波动，因此EOQ 模型需要进一步扩展。
经济订货批量扩展模型（EOQX）是在EOQ 模型基础上，对需求波动的处理。
EOQX 模型假设需求服从泊松分布，订货成本和库存成本仍然与订货数量和库存数量成正比。
II.EOQX 模型假设在EOQX 模型中，我们假设需求波动服从泊松分布。
泊松分布是一种离散型概率分布，用于描述在固定时间内事件发生的次数。
这种分布假设事件发生的概率在任何时间段内都是恒定的，且不同时间段的概率可以相加。
此外，EOQX 模型还假设订货成本和库存成本与订货数量和库存数量成正比。
这一假设与EOQ 模型相同，简化了模型的计算过程。
III.EOQX 模型公式EOQX 模型的公式如下：Q = √(2DS/C) * √(λ/σ)其中：- Q 是经济订货批量- D 是年需求量- S 是每次订货成本- C 是单位商品年保管费用- λ是平均需求率- σ是需求波动率公式推导如下：首先，我们根据泊松分布的性质，计算出需求量λ的期望值和方差：E(λ) = λVar(λ) = λ然后，根据期望值和方差，计算需求波动率σ：σ= √Var(λ) = √λ接下来，我们根据EOQ 模型的公式，计算经济订货批量Q：Q = √(2DS/C)最后，将需求波动率σ代入公式，得到EOQX 模型的公式：Q = √(2DS/C) * √(λ/σ)IV.EOQX 模型应用利用EOQX 模型，我们可以计算出在考虑需求波动的情况下，一次订货的最佳数量。
简述经济订货批量模型的基本原理下载提示：该文档是本店铺精心编制而成的，希望大家下载后，能够帮助大家解决实际问题。
文档下载后可定制修改，请根据实际需要进行调整和使用，谢谢!本店铺为大家提供各种类型的实用资料，如教育随笔、日记赏析、句子摘抄、古诗大全、经典美文、话题作文、工作总结、词语解析、文案摘录、其他资料等等，想了解不同资料格式和写法，敬请关注!Download tips: This document is carefully compiled by this editor. I hope that after you download it, it can help you solve practical problems. The document can be customized and modified after downloading, please adjust and use it according to actual needs, thank you! In addition, this shop provides you with various types of practical materials, such as educational essays, diary appreciation, sentence excerpts, ancient poems, classic articles, topic composition, work summary, word parsing, copy excerpts, other materials and so on, want to know different data formats and writing methods, please pay attention!经济订货批量模型的基本原理引言经济订货批量模型是供应链管理中的关键概念之一，它有助于企业优化库存管理，降低成本，并确保供应链的高效运作。
用经济订单数量（EOQ）模型计算年度订单成本，就像库存管理的隐
藏藏宝图。
EOQ模型是一种很酷的工具，它帮助我们找到完美的订单数量，以尽量减少从订单到持有的所有库存成本。
每年的订单成本就像冒险预算我们所有的寻宝订单全年。
为了找到它，我们使用超级秘密公式：年度订购费用=（定单、定单数量）×每架订购费用。
有了
这个公式，我们可以破解代码，并揭示我们一年的所有订单的总成本。
这就像当我们自己库存故事的英雄，揭开订购成本和拯救一天的奥秘！
该术语（要求、命令数量）将它进一步细分，表明每年有多少订单。
我们用订单数量来划分需求，以确定订单的发布频率。
我们乘以每个
订单的订单成本得到一年的总订单成本。
通过了解这一成本，企业可以做出明智的选择，决定订购多少，订购多少，订购多少，所有成本
都尽可能降低库存成本。
值得注意的是，这种公式假设产品的需求全
年保持不变，而且产品没有时断时续或短缺。
年度订单费用是EOQ模式框架内的一个关键决定因素，有助于企业通过确定最具成本效益的订单数量和频率来优化其库存管理。
通过采用
公式年度订购费用=（要求、命令数量）× 订购费用按订单计算，企
业可以有效地计算在一年之内为库存物品定单所产生的总费用。
这种
战略需求有助于按照现行政策和准则尽量减少总的库存成本，从而促
进对库存的有效管理。
经济订货批量扩展模型公式摘要：1.经济订货批量扩展模型的背景和意义2.经济订货批量扩展模型的公式3.模型的假设条件4.模型的应用和优势5.模型的局限性和改进方向正文：一、经济订货批量扩展模型的背景和意义经济订货批量扩展模型是一种在经济订货批量模型基础上进行改进和优化的模型，旨在更准确地确定企业的订货批量，以实现库存成本的最小化和企业利润的最大化。
在现代供应链管理中，如何在保证供应稳定的同时降低库存成本，是企业面临的重要问题。
因此，研究经济订货批量扩展模型具有重要的理论和实践意义。
二、经济订货批量扩展模型的公式经济订货批量扩展模型的公式为：Q = √((2DS)/C)，其中：Q：经济订货批量D：商品年需求量S：每次订货成本C：单位商品年保管费用三、模型的假设条件经济订货批量扩展模型的假设条件包括：1.企业能及时补充存货，即需要订货时便可立即取得存货；2.所订购的存货均能够一次全额到达，不需陆续入库；3.订货提前期已知，为常量；4.订货费与订货批量无关；5.维持库存费是库存量的线性函数；6.补充率为无限大，全部订货一次交付；7.不允许缺货；8.采用固定量系统。
四、模型的应用和优势经济订货批量扩展模型在实际应用中具有以下优势：1.有助于企业更准确地确定订货批量，降低库存成本；2.考虑了多次订货和库存保管费用等因素，更符合实际情况；3.有助于提高客户满意度，降低缺货风险；4.可为企业提供参考，便于调整库存策略。
五、模型的局限性和改进方向尽管经济订货批量扩展模型在实际应用中具有一定的优势，但仍存在以下局限性：1.模型的假设条件较为理想化，与实际情况可能存在一定差距；2.模型未能充分考虑市场需求波动、价格变动等因素的影响；3.模型对于不同行业的适用性可能存在差异。
因此，企业在应用经济订货批量扩展模型时，需要结合实际情况进行调整和优化，以提高模型的准确性和实用性。
.经济订货批量(Economic Order Quantity,EOQ)又称整批间隔进货模型、EOQ模型经济订货批量概述经济订货批量(EOQ),即Economic Order Quantity是固定订货批量模型的一种，可以用来确定企业一次订货（外购或自制）的数量。
当企业按照经济订货批量来订货时，可实现订货成本和储存成本之和最小化。
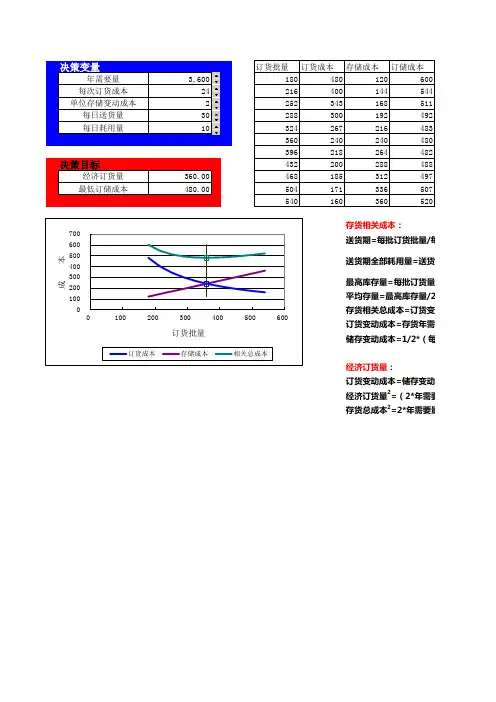
订货批量概念是根据订货成本来平衡维持存货的成本。
了解这种关系的关键是要记住，平均存货等于订货批量的一半。
因此，订货批量越大，平均存货就越大，相应地，每年的维持成本也越大。
然而，订货批量越大，每一计划期需要的订货次数就越少，相应地，订货总成本也就越低。
把订货批量公式化可以确定精确的数量，据此，对于给定的销售量，订货和维持存货的年度联合总成本是最低的。
使订货成本和维持成本总计最低的点代表了总成本。
上述讨论介绍了基本的批量概念，并确定了最基本的目标。
简单地说，这些目标是要识别能够使存货维持和订货的总成本降低到最低限度的订货批量或订货时间。
购进库存商品的经济订货批量,是指能够使一定时期购、存库存商品的相关总成本最低的每批订货数量.企业购、存库存商品的相关总成本包括购买成本、相关订货费用和相关储存成本之和。
经济订货批量模型是目前大多数企业最常采用的货物定购方式.该模型适用于整批间隔进货、不允许缺货的存储问题，即某种物资单位时间的需求量为常D，存储量以单位时间消耗数量D的速度逐渐下降，经过时间T后，存储量下降到零，此时开始定货并随即到货，库存量由零上升为最高库存量Q，然后开始下—个存储周期，形成多周期存储模型.经济订货批量基本公式...其中，Q*为经济订货批量；C为单次订货成本；R为年总需求量；H为单位产品的库存成本.订货费用研究下因订货而支付的费用。
一个规模很小的公司，订购货物的工作只不过由某个人兼任，或者就由公司的老板兼任这项工作。
这就很难把这位兼职的人在其领取的薪金中划出一部分纳入订货的费用之内。
经济订货量模型在库存管理中的应用在当今竞争激烈的商业环境中，有效的库存管理对于企业的生存和发展至关重要。
库存过多会占用大量资金，增加存储成本和风险；库存过少则可能导致缺货，影响销售和客户满意度。
经济订货量模型作为一种重要的库存管理工具，可以帮助企业在满足需求的前提下，优化订货数量，降低成本，提高效益。
一、经济订货量模型的基本原理经济订货量（Economic Order Quantity，EOQ）模型是基于一系列假设条件建立的。
它假设需求是稳定且已知的，每次订货的成本固定，单位存储成本固定，并且货物瞬时补充。
在这些假设下，通过数学计算可以得出使总库存成本最小化的订货量。
总库存成本包括订货成本和存储成本。
订货成本是每次订货时发生的固定费用，如采购人员的工资、运输费用等。
存储成本则是与库存数量相关的费用，如仓库租金、保险费、利息等。
EOQ 模型的计算公式为：EOQ ＝√2×D×S ／ H其中，D 表示年需求量，S 表示每次订货成本，H 表示单位年存储成本。
通过这个公式，我们可以找到一个平衡点，使得订货成本和存储成本之和最小。
二、经济订货量模型的应用步骤1、确定相关参数年需求量：需要对过去的销售数据进行分析和预测，以准确估计未来一年的产品需求。
每次订货成本：包括采购人员的差旅费、通信费、订单处理费等。
单位年存储成本：考虑仓库租金、保险费、损耗、资金占用成本等。
2、计算经济订货量将确定好的参数代入 EOQ 公式，计算出经济订货量。
3、考虑实际情况进行调整EOQ 模型是基于理想假设得出的结果，在实际应用中，可能需要根据企业的具体情况进行调整。
例如，供应商可能有最小订货量的限制，或者企业为了应对不确定性而希望保持一定的安全库存。
4、监控和评估实施经济订货量策略后，要定期监控库存水平、缺货情况和成本变化，评估该策略的效果，并根据实际情况进行必要的调整和优化。
三、经济订货量模型的优势1、降低成本通过优化订货量，减少了订货成本和存储成本，从而降低了总库存成本。
