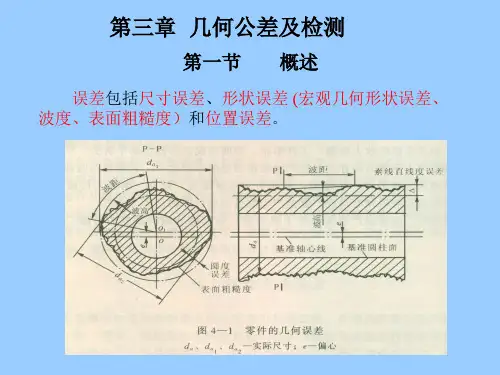
复合位置度

复合坐标的计算公式复合坐标是在数学和物理学中经常遇到的概念，它表示了一个点在不同坐标系下的位置。

在实际应用中，我们经常需要将一个点的位置从一个坐标系转换到另一个坐标系，这就需要用到复合坐标的计算公式。

本文将介绍复合坐标的概念和计算公式，并举例说明其在实际问题中的应用。

首先，我们来看一下复合坐标的概念。

在二维空间中，一个点的位置可以用直角坐标系或极坐标系来表示。

直角坐标系中，一个点的位置由其横坐标和纵坐标确定，而极坐标系中，一个点的位置由其极径和极角确定。

当我们需要将一个点的位置从一个坐标系转换到另一个坐标系时，就需要用到复合坐标的计算公式。

在直角坐标系中，一个点的位置可以表示为(x, y)，而在极坐标系中，一个点的位置可以表示为(r, θ)。

要将一个点的位置从直角坐标系转换到极坐标系，可以使用以下公式：r = √(x^2 + y^2)。

θ = arctan(y/x)。

其中，r表示极径，θ表示极角，arctan表示反正切函数。

这两个公式可以将一个点的位置从直角坐标系转换到极坐标系。

同样地，要将一个点的位置从极坐标系转换到直角坐标系，可以使用以下公式：x = r cos(θ)。

y = r sin(θ)。

其中，cos表示余弦函数，sin表示正弦函数。

这两个公式可以将一个点的位置从极坐标系转换到直角坐标系。

除了在二维空间中的坐标系转换外，复合坐标的概念也可以推广到三维空间中。

在三维空间中，一个点的位置可以用直角坐标系或球坐标系来表示。

直角坐标系中，一个点的位置由其x、y、z坐标确定，而球坐标系中，一个点的位置由其球半径r、极角θ和方位角φ确定。

要将一个点的位置从直角坐标系转换到球坐标系，可以使用以下公式：r = √(x^2 + y^2 + z^2)。

θ = arccos(z/r)。

φ = arctan(y/x)。

同样地，要将一个点的位置从球坐标系转换到直角坐标系，可以使用以下公式：x = r sin(θ) cos(φ)。

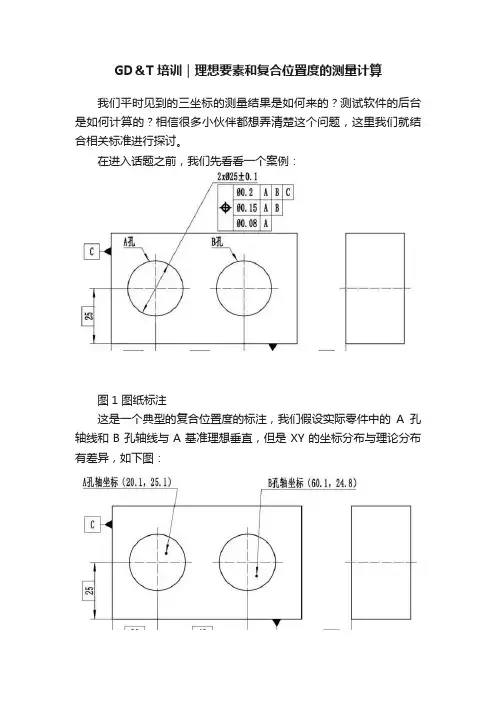
GD＆T培训｜理想要素和复合位置度的测量计算我们平时见到的三坐标的测量结果是如何来的？测试软件的后台是如何计算的？相信很多小伙伴都想弄清楚这个问题，这里我们就结合相关标准进行探讨。

在进入话题之前，我们先看看一个案例：图1 图纸标注这是一个典型的复合位置度的标注，我们假设实际零件中的A孔轴线和B孔轴线与A基准理想垂直，但是XY的坐标分布与理论分布有差异，如下图：图2 实际零件我们的问题是，对于图2所示的实际零件，根据图1的标注，复合位置度的实际测量值应该是多少呢？各位小伙伴在继续往下看之前，可以尝试做去做一做。

再用PCDMIS验证一下是否正确。

我们会在最后公布本题的计算方法和答案，在弄清楚之前，我们先弄清楚理想要素。

1. 理想要素所谓测量的过程就是理想要素和实际被测要素的提取要素的比对过程。

实际被测要素的提取要素很容易理解，就是测试设备在实际零件的被测特征上采的点。

那什么是理想要素呢？它其实就是一个理想的特征，一个理想的点（组），线或轴线（组），面（组），或曲面（组）。

它是怎么来的呢？它可能是拟合出来的，通过切比雪夫法（最大值最小法）自由拟合或者在一定的约束的前提下拟合出来，如形状公差和方向公差的理想要素，可能是人为定义的，如位置度的理想要素，当输入理论值或者坐标值时，理想要素就确定了，也有可能是输入的数模，如评价轮廓度是的3D数据。

不管理想要素是如何来的，但是它和图纸上对应的几何公差的公差带有很多相似的特点。

如在几何公差中，基准能约束公差带的几个自由度，那么理想要素的几个自由度也就被约束了，对于基准不能约束的自由度，则是在保准基准约束优先的前提下由实际被测要素约束（通过最大值最小法拟合）。

相信到这里，会让很多小伙伴一头雾水。

多说无益，我们还是来看看几个案例吧.I. 最小区域法中的理想要素图3 形状公差的理想要素如图3所示的直线度要求，直线度没有基准，所以直线度公差带（相距为0.1的两平行线之间的区域）的自由度没有被约束。

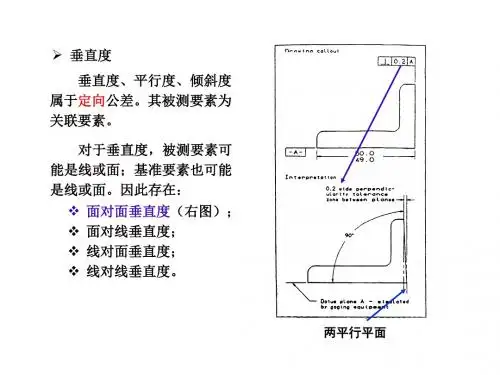
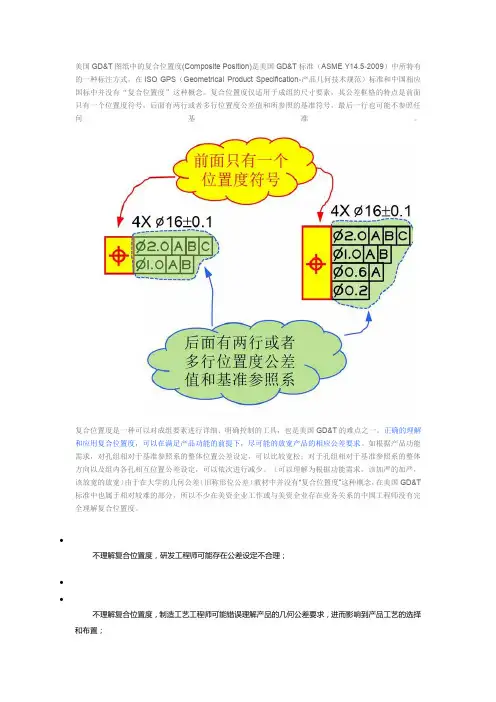
美国GD&T图纸中的复合位置度(Composite Position)是美国GD&T标准（ASME Y14.5-2009）中所特有的一种标注方式，在ISO GPS（Geometrical Product Specification-产品几何技术规范）标准和中国相应国标中并没有“复合位置度”这种概念。

复合位置度仅适用于成组的尺寸要素，其公差框格的特点是前面只有一个位置度符号，后面有两行或者多行位置度公差值和所参照的基准符号，最后一行也可能不参照任何基准。

复合位置度是一种可以对成组要素进行详细、明确控制的工具，也是美国GD&T的难点之一。

正确的理解和应用复合位置度，可以在满足产品功能的前提下，尽可能的放宽产品的相应公差要求。

如根据产品功能需求，对孔组相对于基准参照系的整体位置公差设定，可以比较宽松；对于孔组相对于基准参照系的整体方向以及组内各孔相互位置公差设定，可以依次进行减少。

（可以理解为根据功能需求，该加严的加严，该放宽的放宽）由于在大学的几何公差（旧称形位公差）教材中并没有“复合位置度”这种概念，在美国GD&T 标准中也属于相对较难的部分，所以不少在美资企业工作或与美资企业存在业务关系的中国工程师没有完全理解复合位置度。

•不理解复合位置度，研发工程师可能存在公差设定不合理；••不理解复合位置度，制造工艺工程师可能错误理解产品的几何公差要求，进而影响到产品工艺的选择和布置；••不理解复合位置度，测量工程师可能错误的择测量评价了方法，最终增加了漏判或误判的可能性；••不理解复合位置度，国内供应商在技术评审和报价过程中可能出现“低级”的失误。

•这一切都最终影响到产品质量、时间、成本！理解复合位置度的关键是理解“基准”和“公差带”之间的关系。

对于复合位置度的第一行，按照传统的位置度理解即可：基准既约束公差带的方向（旋转自由度），也约束公差带的位置（平移自由度）。

对于复合位置度公差框格，除了第一行之外的下面几行，基准仅约束公差带的方向（旋转自由度）；基准对于公差带的位置（平移自由度）没有任何限制。

M310-12-1C9.1位置度位置度公差描述的是被测要素实际位置对理想位置允许的变动区域，因此位置度有点的位置度、线的位置度、面的位置度。

而用的最多的是孔组的位置度。

1、公差带的概念：公差带—实际被测要素允许变动的区域。

它体现了对被测要素的设计要求，也是加工和检验的根据当实际被测要素的误差在公差带内合格，超出则不合格。

四个要素公差带的形状(9种形式，t, Φt, sΦt )公差带的大小(宽度，半径差，直径）公差带的方向公差带的位置位置度的评价都是需要基准的，一般箱体类零件的评价都是在三基面体系下进行的。

三基面体系Datum Reference Frame —三个相互垂直的理想(基准)平面构成的空间直角坐标系。

见下图M310-12-1C2、位置度评价方式：下图显示了位置度菜单的各个子菜单群的细节，将逐一介绍各个子菜单群的含义。

在GD&T对话框，可以创建特征控制框（FCF）尺寸信息并将其插入到零件程序中。

当没有选择使用传统尺寸菜单项目时，只要在插入——尺寸子菜单选择一个支持特征控制框的尺寸信息，就弹出GD&T对话框。

对话框包含两个页面，特征控制框和高级，每一个页面包含很多控制项，可以构造特征控制框和相关联的尺寸信息。

PC-DMIS Manual Version 4.3·CAD++ - CMM 1M310-12-1C9.1.1特征控制框页面特征控制框页面可以构造一个特征控制框。

此工具可以帮助定义基准特征，选择用于特征控制框尺寸的特征，并且可以提供一个编辑器来定义在特征控制框用到的特定符号、公差和基准，还可以预览建立的特征控制框的当前状态。

如下列表为此页面不同项目的信息：标识——此功能框显示特征控制框的名称，可以在此进行相应的修改。

特征——此列表显示特定特征控制框类型可用的特征。

一些特征在零件程序中存在，但可能不适用于特定的特征控制框。

例如，在评价圆度时，面特征就不可用。

选择第一个特征后，PC-DMIS会对列表进行相应更新。

面轮廓度的复合位置度
面轮廓度的复合位置度是指在机械加工中，对零件的面轮廓度误差进行综合评估的一种方法。

它的公差带是包络一系列直径为公差值的球的两包络面之间的区域，诸球的球心应位于具有理论正确几何形状的曲面上。

在国家标准GB/T1958-2004中，利用三坐标测量装置测量面轮廓度的方法为：将被测零件放置在仪器工作台上，并进行正确定位。

测出若干个点的坐标值，并将测得的坐标值与理论轮廓的坐标值进行比较，取其中差值最大的绝对值的2倍作为该零件的面轮廓度误差。

复合位置度的测量需要综合考虑零件的理论轮廓和实际轮廓，通过比较两者之间的差异来确定零件的加工误差。

这种测量方法可以有效地提高零件的加工精度和质量，并保证零件的使用性能。

三坐标三坐标--关于复合位置度的测量关于复合位置度的测量邓小锋 郭帅帅( 西安爱德华测量设备股份有限公司 )摘要：本文详细说明了复合位置度的具体意义，GB 中的标示以及在AC-DMIS 中复合位置度检测的原理和方法。

关键词：复合位置度 三坐标 PLTZF FRTZF 阵列位置公差 形体相关公差 孔系一、引言随着制造业的全球化，我们越来越多的会接触到国外的图纸,国外的标注方式.复合位置度就是我们经常碰到的一种美式标注方式。

要了解复合位置度，我们先回顾一下位置度，位置度是指被测要素所在的实际位置对其理想位置的允许变动范围。

位置度公差有点的位置度、线的位置度和面的位置度。

而在实际加工中，孔系阵列的位置度（即复合位置度）则较为常见。

复合位置度公差（如图一） 不仅给出了孔系相对于基准的定位公差，而且给出了各个孔系之间的相互位置公差，与传统的只给出孔系相对于基准的定位公差相比，有较好的经济性，因此得到了广泛的应用。

图一二、复合位置度复合位置度是ASME Y14.5 M 即美国机械工程师学会制定的“尺寸和公差标准”的一种标法，主要应用于阵列形体，即一组具有相同尺寸大小和形状并按一定规律排列的形体。

阵列形体通常需要用上下框格的位置度控制：上框格描述的是阵列形体作为一个整体的位置度公差，称为 阵列位置公差阵列位置公差阵列位置公差 Pattern-Locating Tolerance Zone Framework（PLTZF）下框格描述的是阵列中各个形体相互之间的位置和方向公差，称为 形体相关公差形体相关公差Feature-Relating Tolerance Zone Framework（FRTZF）从英文描述可以看出，上下框的公差都不是针对每一个具体的孔，而是一个几何图框（Framework），上框用于定位（Locating）它是由基准A、B、C 及距离基准的理论尺寸所确定，所确定的几何图框是唯一确定的。

下框是各个孔间的联系（Relating）它由孔间距的理论尺寸所确定，所确定的几何图框不含基准，仅仅是各孔之间的联系。

在实际加工中，孔系阵列的位置度（即复合位置度）则较为常见。

复合位置度公差（如图一）不仅给出了孔系相对于基准的定位公差，而且给出了各个孔系之间的相互位置公差，与传统的只给出孔系相对于基准的定位公差相比，有较好的经济性，因此得到了广泛的应用。

图一二、复合位置度复合位置度是ASME Y14.5 M即美国机械工程师学会制定的“尺寸和公差标准”的一种标法，主要应用于阵列形体，即一组具有相同尺寸大小和形状并按一定规律排列的形体。

阵列形体通常需要用上下框格的位置度控制：上框格描述的是阵列形体作为一个整体的位置度公差，称为阵列位置公差 Pattern-Locating Tolerance Zone Framework（PLTZF）下框格描述的是阵列中各个形体相互之间的位置和方向公差，称为形体相关公差Feature-Relating Tolerance Zone Framework （FRTZF）从英文描述可以看出，上下框的公差都不是针对每一个具体的孔，而是一个几何图框（Framework），上框用于定位（Locating）它是由基准A、B、C及距离基准的理论尺寸所确定，所确定的几何图框是唯一确定的。

下框是各个孔间的联系（Relating）它由孔间距的理论尺寸所确定，所确定的几何图框不含基准，仅仅是各孔之间的联系。

上框的基准用于几何图框的定位，下框的基准用来控制几何图框移动的方向。

下框（FRTZF）内如规定了基准，实际上就是控制了FRTZF相对于PLTZF移动的方向。

如图一中的FRTZF，实际就是表示每个孔相对与基准A的垂直度，不可以相对于A倾斜，但可以在PLTZF中所确定的直径0.8的圆内移动或者旋转。

若FRTZF含有两个基准A和B，那就代表直径为0.25的圆柱体只可以沿C基准方向移动。

最终的目的是通过FRTZF不断的移动使每个孔的轴线处在PLTZF和FRTZF的公差重合区内。

注意，PLTZF是固定不动的。

复合位置度在GB中的标注，如图二，图二 GB中关于孔系的标注在GB中位置度公差针对的仍然是一个几何图框，它由理论正确尺寸按确定的几何关系联系在一起作为一个整体。