机器人学齐次变换矩阵练习题
- 格式:doc
- 大小:31.50 KB
- 文档页数:2


78分1.空间中点的齐次坐标是采用个元素的列阵来描述的(6.0分)A.2B.3C.4D.5我的答案:C√答对2.采用齐次法描述空间中任意矢量的方向,其最后一个元素为(6.0分)A.0B.1C.2D.3我的答案:A√答对3.当机器人关节为移动关节,其关节变量为(6.0分)A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案:B√答对4.机器人运动学正问题是(6.0分)A.已知关节变量求取末端位姿B.已知末端位姿求取关节变量C.已知关节力求取末端位姿D.已知末端位姿求取关节力我的答案:A√答对5.当机器人关节为转动关节,其关节变量为(6.0分)A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案:D×答错1.机器人运动学逆问题可用以(8.0分))A.求取机器人末端位姿B.求取机器人关节变量C.求取机器人工作空间D.用以实现机器人控制我的答案:BD√答对2.齐次矩阵可用以描述(8.0分))A.一个坐标系相对于另一个坐标系的位姿B.刚体在空间中的位姿C.刚体的一系列运动D.关节与末端位姿的变换关系我的答案:ABD×答错3.机器人关节变量一般为(8.0分))A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案:BC√答对4.机器人连杆参数包括(8.0分))A.连杆长度B.连杆距离C.连杆转角D.连杆扭角我的答案:ABCD√答对5.机器人运动学正问题可用以(8.0分))A.求取机器人末端位姿B.求取机器人关节变量C.求取机器人工作空间D.用以实现机器人控制我的答案:AD×答错1.连杆坐标系是建立在连杆上,与连杆固定连接的坐标系(6.0分)我的答案:正确√答对2.机器人运动学用以建立末端位姿与关节变量之间的关系(6.0分)我的答案:正确√答对3.描述刚体位姿的齐次矩阵是一4*4的矩阵(6.0分)我的答案:正确√答对4.在齐次变换中,如果相对于固定坐标系运动,需右乘变换算子(6.0分)我的答案:错误√答对5.运动学正问题是已知机器人末端位姿求各关节运动变量(6.0分)我的答案:错误√答对。

一、选择题(4选1,多于4个的为多选题;共20分,每小题2分)1.机器人的定义中,突出强调的是1).具有人的形象2).模仿人的功能3).像人一样思维4).感知能力很强2.一个刚体在空间运动具有几个自由度?1).3个2).4个3).5个4).6个3.运动逆问题是实现如下变换:1).从关节空间到操作空间的变换2).从操作空间到迪卡尔空间的变换3).从迪卡尔空间到关节空间的变换4).从操作空间到任务空间的变换4.对于有规律的轨迹,仅示教几个特征点,计算机就能利用________获得中间点的坐标。
1).优化算法2).平滑算法3).预测算法4).插补算法5.完整的传感器应包括下面哪三部分?1).敏感元件2).计算机芯片3).转换元件4).模数转换电路5).基本转换电路6).微波通信电路6.压电式传感器,即应用半导体压电效应可以测量1).电压2).亮度3).力和力矩4).距离7.用于检测物体接触面之间相对运动大小和方向的传感器是:1).接近觉传感器2).接触觉传感器3).滑动觉传感器4).压觉传感器8.机器视觉系统主要由三部分组成:1).图像的获取2).图像恢复3).图像增强4).图像的处理和分析5).输出或显示6).图形绘制9.示教—再现控制为一种在线编程方式,它的最大问题是:1).操作人员劳动强度大2).占用生产时间3).操作人员安全问题4).容易产生废品10.集控式足球机器人的智能主要表现在哪两个子系统?1).机器人小车子系统2).机器人通信子系统3).机器人视觉子系统4).机器人决策子系统5).机器人总控子系统二、判断题(回答Y/N;共30分,每题2分)1.工业机器人亦称之为操作机。
2.机器人的自由度数目就是机器人所具有独立坐标轴运动的数目.3.高维向量是由高维空间扩展而成的。
4.如果是相对于手坐标系H的运动,其相应的齐次变换矩阵左乘原齐次变换矩阵。
5.机构关节数的计算是将全部主动关节和被动关节数求和。


![第2章 机器人运动学—数学基础[可打印版,含习题]](https://uimg.taocdn.com/c5aed3c4a1c7aa00b52acbd8.webp)

第三章作业题1.试判断下列矩阵是否是正交矩阵?1) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-100001010 2) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-010100001 3) ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡110001100 解:将矩阵乘其转置矩阵,乘积为单位矩阵,故为正交矩阵;如果不是单位阵,则不是正交矩阵。
计算结果:1)、2)、为正交矩阵,3)不是。
2.齐次矩阵表示为⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--100?201?100?010?,利用齐次矩阵的性质求出矩阵中“?”符号的元素。
3. 已知R 为旋转矩阵,b 为平移向量,试写出相应的齐次矩阵。
⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=010100001R ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=523b解:齐次矩阵为4.当动坐标先绕基坐标Z 轴转动90度,再绕基坐标X 轴转动-90度,再在基坐标上移动(3,7,9)。
试用齐次坐标法描述当前动坐标的位姿。
解:由于 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000010000010010)90,( z Rot ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=-10000100100001)90,( x Rot ,⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000910070103001)973(Trans ,则表示动坐标位姿的齐次矩阵 )90,()90,()973(︒*︒-*=z Rot x Rot Trans A ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-*⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=1000900171003010100001000001001010009010710030011000010000010010*100000100100000110009100701030015.手坐标上的向量a=[0 2 0]T ,先沿基坐标Y B 轴移动10为b ,再分别绕基坐标X B 轴和手坐标X H 轴转-90︒分别为c 和d ,试通过齐次变换矩阵,计算该向量变换后的基座标值。

成绩:《工业机器人》大作业学期:2014~2015学年第一学期指导教师:李敏姓名:学号:年级、专业:2011级机制班西南交通大学峨眉校区机械工程系2.6 已知齐次变换矩阵H=0100001010000001⎡⎤⎢⎥-⎢⎥⎢⎥-⎢⎥⎣⎦要求ot(,)R θƒ=H 。
确定ƒ和θ的值解:0100001010000001H ⎡⎤⎢⎥-⎢⎥=⎢⎥-⎢⎥⎣⎦,∴由式(2.46)得001x y z n n n =⎧⎪=⎨⎪=-⎩;100x y z o o o =⎧⎪=⎨⎪=⎩;010x y z a a a =⎧⎪=-⎨⎪=⎩; 由式(2.48)得:111cos (1)(0001)222x y z n o a θ=++-=++-=- 又:把旋转规定为绕矢量ƒ的正向旋转,使得0≤θ≤180 ,故120θ= 。
由式(2.52)得:2sin 3z y x o a θ-ƒ===2sin x z y a n θ-ƒ===;2sin 3y x z n o θ-ƒ===-综上,=⎡⎤⎢⎥⎢⎥⎢⎥ƒ⎢⎥⎢⎢⎢⎢⎥⎣⎦,120θ=。
2.10 {A}和{B}两坐标系仅仅方向不同。
坐标系{B}是这样得到的:首先与坐标系{A}重合,然后绕单位矢量ƒ旋转θ弧度,即()AA B B R R θ=ƒ,求证A B R e θƒ= ,式中 000z y zx y x⎡⎤-ƒƒ⎢⎥ƒ=ƒ-ƒ⎢⎥⎢⎥-ƒƒ⎣⎦ 证明:cos sin f e f θθθ=+ 且000zy zx y xf f f f f f f ⎡⎤-⎢⎥=-⎢⎥⎢⎥-⎣⎦0sin sin cos sin 0sin sin sin 0z y f z x y x f f e f f f f θθθθθθθθ⎡⎤-⎢⎥∴=+-⎢⎥⎢⎥-⎣⎦···········(a )根据式(2.45)和式(2.47),令=ot()R R θƒ, 即0000000101xx x x x y x z z x y y y y x yz y y z y x z z z x z y y z x z z n o a f f vers c f f vers f s f f vers f s n o a f f vers f s f f vers c f f vers f s n o a f f vers f s f f vers f s f f vers c θθθθθθθθθθθθθθθθθθ+-+⎡⎤⎡⎤⎢⎥⎢⎥++-⎢⎥⎢⎥=⎢⎥⎢⎥-++⎢⎥⎢⎥⎣⎦⎣⎦··(b ) 由已知:()A A B B R R θ=ƒ,,将此式作式(b )变换,可得=0x y f f vers θ,即cos =0θ1-,则=90θ 。

1.1 点矢量v 为]00.3000.2000.10[T ,相对参考系作如下齐次坐标变换:A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0 写出变换后点矢量v 的表达式,并说明是什么性质的变换,写出旋转算子Rot 及平移算子Trans 。
解:v ,=Av=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100.3000.2000.10=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡13932.1966.9 属于复合变换:旋转算子Rot (Z ,30̊)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000010000866.05.0005.0866.0 平移算子Trans (11.0,-3.0,9.0)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000.91000.30100.110011.2 有一旋转变换,先绕固定坐标系Z 0 轴转45̊,再绕其X 0轴转30̊,最后绕其Y 0轴转60̊,试求该齐次坐标变换矩阵。
解:齐次坐标变换矩阵R=Rot(Y ,60̊)Rot (X ,30̊)Rot(Z ,45̊)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000010000707.0707.000707.0707.010000866.05.0005.0866.000001100005.00866.000100866.005.0=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----10000433.0436.0436.005.0612.0612.00750.0047.0660.0 1.3 坐标系{B}起初与固定坐标系{O}相重合,现坐标系{B}绕Z B 旋转30̊,然后绕旋转后的动坐标系的X B 轴旋转45̊,试写出该坐标系{B}的起始矩阵表达式和最后矩阵表达式。
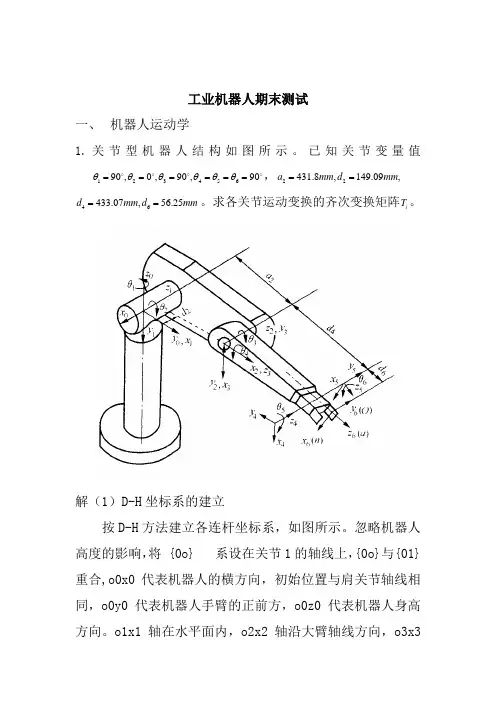
工业机器人期末测试一、 机器人运动学1. 关节型机器人结构如图所示。
已知关节变量值12345690,0,90,90θθθθθθ====== ,22431.8,149.09,a mm d mm ==46433.07,56.25d mm d mm ==。
求各关节运动变换的齐次变换矩阵i T 。
解(1)D-H 坐标系的建立按D-H 方法建立各连杆坐标系,如图所示。
忽略机器人高度的影响,将 {0o} 系设在关节1的轴线上,{0o}与{01}重合,o0x0代表机器人的横方向,初始位置与肩关节轴线相同,o0y0 代表机器人手臂的正前方,o0z0 代表机器人身高方向。
o1x1 轴在水平面内,o2x2 轴沿大臂轴线方向,o3x3轴与小臂轴线垂直,o4x4∥o5x5∥o6x6。
坐标原点o2、o3与o4、o5重合。
o6x6y6z6为终端坐标系,该坐标系考虑了工具长度d6。
(2)确定各连杆的D-H参数(3)求两杆之间的位姿矩阵Ti11010 1010 0-100 0001 c ss cT-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2222220222020010001c s a cs c a sTd-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦33030 3030 0100 0001 c ss cT⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦44404040400-100001c ss cTd-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦55050505000100001c ss cT⎡⎤⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦66660066000010001c ss cTd-⎡⎤⎢⎥⎢⎥=⎢⎥⎢⎥⎣⎦2.如图二自由度平面机械手,已知手部中心坐标值为(),x y。
求11该机械手运动方程的逆解θ及1d。
1二、机器人动力学1.如图二自由度平面机械手,已知杆长120.5l l m==,相关参数如下表所示。
求表中两种情况下的关节瞬时速度1θ∙和2θ∙。
2. 已知二自由度平面机械手的雅可比矩阵为112222112222sin sin sin cos cos cos l l l J l l l θθθθθθ---⎡⎤=⎢⎥+⎣⎦。

一、简答题
1.什么是机器人的内部传感器和外部传感器?举例说明之。
2. 按机器人的开发内容与应用进行分类,机器人应分为那几类?分别举例说明之。
3.齐次向量是怎样定义的?试举例说明之。
二、计算题
1.一个两关节机器人,关节1、2的齐次变换矩阵分别为A1和A2,试求该机器人的坐标变换矩阵。
2.已知R 为旋转矩阵,b 为平移向量,试写出相应的齐次矩阵。
三. 设计题:
1、MSO —CP -020型垂直六关节机器人的坐标结构简图如图1所示,其各连杆的D -H 参数和关节变量列于表1,(1)写出连杆D-H 参数及关节变量;(2)求出各连杆坐标系间变换矩阵A i ;(3)并写出机器人运动学方程。
111
11c 0s 0s 0c 001000
00
1θθθθ-⎡⎤⎢⎥⎢⎥=⎢⎥-⎢⎥⎣⎦A 2
2
222
2c 0s 0s 0c 00100
00
1d θθθθ⎡⎤
⎢⎥-⎢⎥=⎢⎥⎢⎥⎣⎦
A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=010100001R ⎥⎥
⎥⎦⎤
⎢⎢⎢⎣⎡--=523b
图1:垂直六关节机器人的坐标结构简图表1:连杆D-H参数及关节变量。
举例说明运用齐次变换矩阵求解机器人正运动学的方法齐次变换矩阵用于描述刚体在空间中的位姿(位置和方向)。
在机器人正运动学问题中,运用齐次变换矩阵可以求解机器人末端执行器的位姿。
我们以一个简单的2R(两个旋转关节)机械臂为例进行说明。
假设2R机械臂有两个关节q1和q2,臂长分别为L1和L2。
我们的目标是求解两个关节角度q1和q2下,末端执行器的位置坐标(x, y)和方向theta。
首先,我们需确定两个坐标系。
通常将基坐标系(frame0)放在第一个关节处,frame1放在第二个关节处,frame2放在末端执行器处。
然后,我们需要分别计算从frame0到frame1的齐次变换矩阵T01和从frame1到frame2的齐次变换矩阵T12。
T01表示frame1相对于frame0的位姿,其旋转角度为q1,平移距离为L1。
矩阵形式如下:```T01 = | cos(q1) -sin(q1) 0 L1*cos(q1) || sin(q1) cos(q1) 0 L1*sin(q1) || 0 0 1 0 || 0 0 0 1 |```同理,T12表示frame2相对于frame1的位姿,其旋转角度为q2,平移距离为L2。
矩阵形式如下:```T12 = | cos(q2) -sin(q2) 0 L2*cos(q2) || sin(q2) cos(q2) 0 L2*sin(q2) || 0 0 1 0 || 0 0 0 1 |```接下来,我们需要计算从frame0到frame2的齐次变换矩阵T02。
通过矩阵乘法,我们可以得到:```T02 = T01 * T12```最后,我们从T02矩阵中提取机器人末端执行器的位置和方向。
位置坐标(x, y)就是T02矩阵中的平移部分,即:```x = T02[0][3]y = T02[1][3]```方向theta可以通过以下公式计算:```theta = atan2(T02[1][0], T02[0][0])```所以,通过齐次变换矩阵,我们可以求解出机器人末端执行器的位置和方向,从而解决2R机械臂的正运动学问题。
3-1.点矢量v 为]00.3000.2000.10[T,相对参考系作如下齐次坐标变换:A=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0 写出变换后点矢量v 的表达式,并说明是什么性质的变换,写出其经平移坐标变换和旋转变换后的其次坐标变换矩阵(即写出旋转算子Rot 及平移算子Trans )。
解:v ,=Av=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--10000.9000.1000.0000.00.3000.0866.0500.00.11000.0500.0866.0⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡100.3000.2000.10=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡13932.1966.9 属于复合变换:旋转算子Rot (Z , )=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-1000010000866.05.0005.0866.0 平移算子Trans (11.0,-3.0,9.0)=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-10000.91000.30100.110013-2 . 有一旋转变换,先绕固定坐标系Z 0 轴转 ,再绕其X 0轴转 ,最后绕其Y 0轴转 ,试求该齐次坐标变换矩阵。
解:齐次坐标变换矩阵R=Rot(Y , )Rot (X , )Rot(Z , ) =⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-100010000707.0707.000707.0707.010000866.05.0005.0866.000001100005.00866.000100866.005.0=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----10000433.0436.0436.005.0612.0612.00750.0047.0660.0 3-3. 坐标系{B}起初与固定坐标系{O}相重合,现坐标系{B}绕Z B 旋转 ,然后绕旋转后的动坐标系的X B 轴旋转 ,试写出该坐标系{B}的起始矩阵表达式和最后矩阵表达式。
一、解:⒈坐标系{j}与{i}沿矢量 平移的齐次 变换矩阵:⒉坐标系{j}与{i}绕x 轴旋转 的齐次变换矩阵:⒊坐标系{j}与{i}绕z 轴旋转 的齐次变换矩阵:⒋坐标系{j}与{i}先沿矢量 平移,再绕x 轴旋转 的齐次变换矩阵:二、已知坐标系{j}是由坐标系经过以下变换得到的:{i}坐标系先绕z 轴旋转 ,然后绕x 轴旋转 ,最后沿坐标系的y 轴平移2个单位。
要求: 1、确定坐标系{i}到坐标系{j}的齐次变换矩阵;2、若已知P 点在坐标系{i}中的位置矢量为 ,则在坐标系{j}中P 点的位置矢量的 各坐标分量分别为多少?解:1、确定坐标系{i}到坐标系{j}的齐次变换矩阵:⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000610018010120011M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=100002123002321000011000060cos 60sin 0060sin 60cos 000013M k j i p i 61812-+=60⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=10000100002321002123100001000030cos 30sin 0030sin 30cos 3 M ⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=1000122321082123060011000030cos 30sin 0030sin 30cos 00001100012000800060014M 30k j i p i 1286+-= 30T i p )1,10,3(=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡-=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡-=100001002010000110000010010000011000090cos 90sin 0090sin 90cos 000011000010000010010100001000090cos 90sin 0090sin 90cos 321M M M1、确定坐标系{i}到坐标系{j}的齐次变换矩阵:2、两坐标系关系为:三、已知三自由度机器人如图所示。
A3-1.写出齐次变换矩阵 T,它表示相对固定坐标系{A}作以下变换。
B1) 绕Z 퐴轴旋转 90°; 2) 再绕X 퐴轴转-90°;푇3) 最后做移动【3 7 9 】;A3-2.写出齐次变换矩阵 T,它表示相对坐标系{B}做以下变换。
B 푇1) 移动【3 7 9 】;2) 绕X 퐵轴旋转-90°; 3) 绕Z 퐵轴转 90°。
3-3.求下面齐次变换的逆变换푇−1 0 1 0 −10 0 −1 2 −1 0 0 0 T = []13-4.已知 0.25 0.43 0.86 5.0A B T 0.87 −0.50 0 −4.0= [ ] 0.43 0.75 −0.50 3.0 0 0 0 1A求 T的第(2,4)元素.B3-5 已知矩阵? 0 −1 0 ? 0 0 1 ? −10 2 ?1] [代表齐次坐标变换,求其中的未知元素值(第一列元素)。
푈3-6 设工件相对于参考系{U}的描述为T,机器人基座相对于参考系푃푈的描述为T,已知B010−1100100−12−1000푈=[푇푃0105푈]푃=[]퐵001900010001要求机器人手爪坐标系{H}与工件坐标系{P}重合,试求变换퐻퐵푇3-7. 已知坐标变换矩阵푈퐴푇,퐵퐴푇,푈퐶푇.0.866−0.50001110000.5000.8660−100.866−0.50010푈=[]퐵퐴푇=[푇] 퐴001800.5000.866−200001000 10.866−0.5000−30.4330.750−0.5−3퐶=[푇]푈0.2500.4330.86630001画出空间尺寸链图,并求퐵퐶푇.3-8.如图3-17 所示的多面体顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4,5).3-9. 如图3-18 所示的多面体各顶点坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3,4).3-10. 如图3-19 所正方体的顶点和中心坐标系,试求4x4 的齐次变换矩阵푖−1푖푇和0푖푇(i=1,2,3)。