当前位置：文档之家 › 第三章 位姿描述和齐次变换.

第三章 位姿描述和齐次变换.

  • 格式：ppt
  • 大小：3.10 MB
  • 文档页数：46

下载文档原格式

  / 46

合集下载

机器人学技术基础课程-位姿描述和齐次变换

机器人学技术基础课程-位姿描述和齐次变换
2、齐次变换在研究空间机构动力学、机器人控制算法、计算 机视觉等方面也得到广泛应用。
位姿描述与齐次变换
1 刚体位姿的描述 2 坐标变换 3 齐次坐标系和齐次变换 4 齐次变换矩阵的运算 5 变换方程
2.1 刚体位姿的描述
为了完全描述一个刚体在空间的位姿，通常将刚体与某 一坐标系固连，坐标系的原点一般选在刚体的特征点上，如 质心、对称中心等。
YˆB ZˆA
ZˆB Xˆ A ZˆB YˆA

ZˆB ZˆA

XB n
2.1.4 旋转矩阵的意义
若坐标系B可由坐标系A,通过绕A的某一坐标轴获得,则绕 x,y,z三轴的旋转矩阵分别为：
1 0 0
c 0 s
c s 0
R(x, ) 0
Ay
y
所以： A Axaˆx Ayaˆy Azaˆz
2.1.2 方位的描述
矢量： A Axaˆx Ayaˆy Azaˆz
模的计算： | A | Ax2 Ay2 Az2
z
Az
A

方向角与方向余弦：, ,
o

Ay
Ax

y
x
cos Ax = A aˆx , cos Ay = A aˆy , cos Az A aˆz
两矢量的叉积又可表示为：
aˆx aˆy aˆz A B Ax Ay Az
Bx By Bz
2.1.2 方位的描述
空间物体B的方位(Orientation)可由某个固接于此物体的坐标系{B}的三 个单位主矢量[xB,yB,zB]相对于参考坐标系A的方向余弦组成的3x3矩阵描述.
BAR n o a a

工业机器人运动学

工业机器人运动学

注意：对于旋转关节，绕z 轴的旋转角 （ θ角）是关节变量。对于滑动关节， 沿 z轴的连杆长度d 是关节变量；
3.8 机器人正运动学方程的D-H参数表示法
一.连杆坐标系的建立
本地参考坐标系步骤：
（1）通常关节不一定平行或相交。因此 ，通常z轴是斜线，但总有一条距离最短的 公垂线，它正交于任意两条斜线。通常在 公垂线方向上定义本地参考坐标系的x轴。 所以如果an表示 zn-1与zn之间的公垂线， 则xn的方向将沿an 。同样，在 zn与 zn+1之 间的公垂线为，xn+1的方向将沿an +1。
3T6


S4C5C6

C4 S6

S5C6 0
S4C5S6 C4C6 S5S6 0
S4S5 C5 0
0
0 1
C1 0 S1 0
A1


S1 0
0 1
C1 0
0 0

0
0
0
1
3.8 机器人正运动学方程的D-H参数表示法
nx = C1 [ C2 ( C4C5C6 - S4S6 ) - S2S5C6 ] - S1( S4C5S6 + C4S6 ) ny = S1 [ C2 ( C4C5C6 - S4S6 ) - S2S5C6 ] + C1( S4C5S6+C4S6 ) nz = -S2 ( C4C5C6 - S4S6 ) - C2S5C6 ox = C1 [ -C2 ( C4C5S6 + S4C6 ) + S2S5C6 ] - S1( -S4C5S6 + C4S6 ) oy = S1 [ -C2 ( C4C5C6 + S4C6 ) + S2S5S6 ] + C1( -S4C5S6 + C4S6 ) oz = S2 ( C4C5C6 + S4C6 ) + C2S5S6 ax = C1 ( C2C4S5 + S2C5 ) – S1S4C5 ay = S1 ( C2C4S5 + S2C5 ) + C1S4S5 az = –S2C4S5 + C2C5 px = C1S2d3 – S1d2 py = S1S2d3 + C1d2 pz = C2d3

机器人运动学坐标变换

机器人运动学坐标变换

xi cos x j sin y j 0 z j yi sin x j cos y j 0 z j zi 0 x j 0 y j 1 z j
2017年2月19日星期日
工 业 机 器 人
第3章
3.2.1 直角坐标变换
工 业 机 器 人
第3章
3.1.1 机器人位姿的表示
姿态可h ｏ ｐ(ｘ,ｙ,ｚ) h
ｏ ｙh ｙ
3.1 机器人的位姿描述
ｚ
余弦值组成3×3的姿态
矩阵来描述。
cos(x , x h ) cos(x , yh ) cos(x , z h ) R cos(y , x h ) cos(y , yh ) cos(y , z h ) cos(z , x h ) cos(z , yh ) cos(z , z h )
2017年2月19日星期日
工 业 机 器 人
R
x , ij
第3章
3.2.1 直角坐标变换
2、旋转变换
②绕x轴旋转α角的 旋转变换矩阵为：
机器人运动学
ｚi
3.2 齐次变换及运算
ｚj
α
0 0 1 0 cos sin 0 sin cos
ｘj
ｙj ｏi ｏj
xi x j cos y j sin yi x j sin y j cos zi z j
ｘi
ｙi
ｘj
2017年2月19日星期日
工 业 机 器 人
第3章
3.2.1 直角坐标变换
2、旋转变换
机器人运动学
3.2 齐次变换及运算
① 绕z轴旋转θ角 若补齐所缺的有些项，再作适当变形，则有：

第三章 数学基础—齐次坐标和齐次变换New2

第三章 数学基础—齐次坐标和齐次变换New2

解1：用画图的简单方法
解2：用分步计算的方法 ① Rot（x, 90°）
1 0 P' 0 0 0 0 0 -1 1 0 0 0 0 1 1 2 3 0 0 3 2 1 1 1
（3-1）
o
i
n
a
运动学正逆求解问题
Where is my hand?
运动学正问题
Direct Kinematics HERE!
How do I put my hand here?
运动学逆问题
Inverse Kinematics: Choose these angles!
3.2 位置和姿态的描述
一、位置描述 对于直角坐标系 {A} ，空间内任一点 P 的位置可有 3×1 的列 A 向量rP （或位置向量）
中各轴的投影分量，很容易得到在重合时，有：
1 0 0 R 0 1 0 0 0 1
由图2-5可知， jv 在y轴上的投影为
k z cos
j y cos
， jv 在z轴上的投影
为 k z sin , kw 在y轴上的投影为 j y sin ， kw 在z轴上的投影为 ，所以有：
② Rot（z, 90°）
0 - 1 1 0 P '' 0 0 0 0
0 0 P ''' - 1 0 0 1 0 0
0 0 1 0
1 0 0 0
0 1 3 3 1 0 0 2 2 1 1 1
A B
T
A
B rP A T rP B
A B
T
理解： 1 ）是 {A} 和 {B} 两个坐标系下点或方位齐次坐标的线性映 射，一旦这两个坐标系之间的位姿关系确定，它也就确定 了。 2）是{B}坐标系相对{A}坐标系的位姿矩阵。

[课件](工业机器人)位姿描述与齐次变换PPT

[课件](工业机器人)位姿描述与齐次变换PPT
六、齐次表达
根据几何学知识，上面第四小节中给定点的绝对位置为：
Ap b a b a b a c s cs b a
写成三维形式，有：
a a a c s 0a Apbbbs c 0b
3. 试按照运动顺序计算相关基本变换矩阵相乘结果
c s 0 a
Tra(An a,A sb,A0)Ro(zA t,)s0
c
0
0 b 1 0
0
1
4. 计算结果比较
两种方法结果相同！但后一种方法简单！
问题：是否仅仅按照运动变换顺序将相关的基本变 换矩阵相乘，即可以得到齐次变换阵？
0 0 0 0 0 10
O B 在A中位置，记作 A pOB
B在
A 中姿态，记作
A B
R
。
分成两块，不便于记忆！
齐次变换矩阵
若写成如下齐次形式，有：
c s 0 aa
A 1ps0 0
c
0 0
0 1 0
A 中的位置，然后与
b
A坐标原点值相加即可
得到该点绝对位置。
OA
由几何法，得：
aacbs 写成矩阵形式
b as bc

Y A
YB
b
b
XB a

OB
a
X A
a
XA
相
a c sa 对
bs cb
坐 标 值
b 1 0b 1 0B A 0R
Ap 1OBB 1pA BTB 1p
七、齐次变换矩阵
1. 构成：分为4块。左上角是姿态矩阵，为一单位正交 矩阵；右上角为对象坐标系原点位置值；左下角为 三个0 0 0，简记为0；右下角为1。

第3章 机器人位姿的数学描述与坐标变换

第3章 机器人位姿的数学描述与坐标变换

x=a(1-cos) , y=a(1-sinθ)
第3章 机器人位姿的数学描述与坐标变换
3.1 机器人位姿的数学描述
#假设机器人的连杆和关节都是刚体 （1）首先，建立一个参考坐标系； （2）然后，在刚体上任意建立一个刚体坐标系。
Z Z'
O' Y'
O
X'
X Y
第3章 机器人位姿的数学描述与坐标变换
刚体位置：
,
)
=
？
j i
R(,q
,
)
=
R(Z
,
)
R(Y
,q
)R(Z
,
)
绕动坐标轴依次转动时，每 个旋转矩阵要从左往右乘。
Z2
Zj
Zi (Z1)
q
q
Yj
（Y2 )
q Y1
Yi
Xi
X1 X2 X j
第3章 机器人位姿的数学描述与坐标变换
cos − sin 0 cosq 0 sinq cos − sin 0
R(Z
i
,q
)
=
s
inq
cosq
0
0
0 1
Zi Zj
q Xi
Xj
Yj q
Yi
第3章 机器人位姿的数学描述与坐标变换
1 0
0
j i
R(
X
i
,q
)
=
0
cosq
−
s in q
0 sinq cosq
cosq 0 sinq
j i
R(Yi
,q
)
=
0
1
0
− sinq 0 cosq

3机器人的位姿描述与坐标变换

3机器人的位姿描述与坐标变换
利用旋转矩阵的正交性质:
假设：
整理得：
旋转变换通式
讨论：
（1）
（2）
（3）
例：坐标系B原来与A重合，将坐标系B绕过原点O的轴线
转动
，求旋转矩阵
解答：
1）
2）
3）带入旋转通式得：
2、等效转轴与等效转角
转轴和转角
旋转矩阵
1
2？
1）将方程两边矩阵的主对角线元素分别相加，则
2）将方程两边矩阵的非对角线元素成对相减得：
►绕多个坐标轴旋转的转动矩阵
1）、绕固定坐标系旋转
2）、绕运动坐标系旋转
ZYZ欧拉角
注意：多个旋转矩阵连乘时，次序不同则含义不同。1）绕新的动坐标轴依次转动时，每个旋转矩阵要从左往右乘，即旋转矩阵的相乘顺序与转动次序相同；2）绕旧的固定坐标轴依次转动时，每个旋转矩阵要从右往左乘，即旋转矩阵的相乘顺序与转动次序相反。
解：
1）
2）
Z
i
X
i
Y
i
P
坐标系j由坐标系i旋转而成
求点P在i坐标系的坐标：
已知点P在j坐标系的坐标：
P
☺
►姿态矢量矩阵
坐标系j相对于i的方位
旋转矩阵的性质：
旋转矩阵
►绕一个坐标轴旋转的转动矩阵
1）RX
2）RY
3）RZ
转动矩阵的特点：(1) 主对角线上有一个元素为1，其余均为转角的余弦/正弦；(2) 绕轴转动的次序与元素1所在的行、列号对应；(3) 元素1所在的行、列，其它元素均为0；(4) 从元素1所在行起，自上而下，先出现的正弦为负，后出现的为正，反之依然。
2、变换矩阵T的相乘 ★矩阵相乘的顺序一般不可换，特殊可换的情况为变换都是同参考系下的平移或绕同一坐标轴的旋转。

机器人运动学

机器人运动学


R3
Z
三个平移自由度 T1, T2, T3
三个旋转自由度 R1, R2, R3
T3
T1
T2
Y R2
X
2019/3/31
R1
2.2 刚体位姿描述
方位描述
第三章
机器人运动学
利用固定于物体的坐标系描述方位 (orientation)。方位又称为姿 态 (pose)。
在刚体 B上设置直角坐标系 {B} ，利用与 {B} 的坐标轴平行 的三个单位矢量表示B的姿态。
A
p R ( x , ) p
B
zB
zA

Bp
P
yB

{A}
1 0 R ( x , ) 0 c 0 s
c R ( y , ) 0 s 0 s 1 0 , 0 c
0 s c
s c 0 0 0 1
2019/3/31
i A iB A jB r11 r12
第三章
机器人运动学
2.2 刚体位姿描述
位置与姿态的表示 相对于参考坐标系{A}，坐标系{B}的原点位置和坐标轴的 方位可以由位置矢量和旋转矩阵描述。刚体B在参考坐标 系{A}中的位姿利用坐标系{B}描述。
{ B}
当表示位置时 当表示方位时
zA
iB
jB
A
kA 坐标系{B}的三个单位主矢量在坐标系{A}中的描述：
pBo
kB
yA
{ A iB , A jB , A k B }
坐标系{B}相对于坐标系{A}的姿态描述：
A B
O
R { iB , jB , k B }
A A A

位姿描述和齐次变换

位姿描述和齐次变换
1. 方向角与方向余弦 OA a OB b =AOB(0)为 向量
a
， b
的夹角，记作
(a , b )
O
A B
=
方向角的余弦称为其方向余弦.
x cos r
x x2 y2 z 2
z
o
r


r r r
u
i x i 定义 旋转矩阵为：R j y i k i z
i x jv j y jv k z jv
数学基础
机械手作为执行机构是用来保证复杂空间运动的综合刚体，而 且它自身也往往需要在机械加工或装配等过程中作为统一体进行 运动。因此，我们需要一种用以描述单一刚体位移、速度和加速 度以及动力学问题的有效而又方便的数学方法---矩阵法 数学描述是以四阶方阵变换三维空间点的齐次坐标为基础的， 能够将运动、变换和映射与矩阵运算联系起来
Y(orientation
)
x(normal)
z(approach)
A B
a o R n
(2.9)
手抓坐标系
Y(orientation ) x(normal) z(approach)
A B
a o R n
平移坐标变换
前面讨论的是在一个坐标系中位姿的描述，在大量的机器人问题中，涉及到 用不同的坐标系来描述同一个刚体的位置及姿态问题，这就涉及到从一个坐 标系的描述到另一个坐标系的描述之间的变换关系，这种变换关系包括：平 移变换和旋转变换
一旦建立了一个坐标系，我们就能够用某个3×1位置矢量来确定该空 间内任一点的位置。对于直角坐标系{A}，空间任一点p的位置可用3×1的 列矢量AP表示。其中，px、py、pz入是点p在坐标系{A}中的三个坐标分量。 Ap的上标A代表参考坐标系{A}。我们称Ap为位置矢量，见图2．1。

3位置描述和齐次变换

3位置描述和齐次变换

3.3齐次变换矩阵的运算和给定的坐标系{A},{B}和{C},已知{B}相对{A}的 描述为 ,{C}相对{B}的描述为 ,则


从而定义复合变换
变换矩阵相乘不满足“交换律”

绝对变换:当坐标系C前乘(左乘)变换T时,TC得到的
是C始终相对于同一参考系的变换,变换的动作顺序
由T的最后(最右)因子开始,以最前(最左)的因子结 束其变换.

相对变换:当坐标系C后乘(右乘)变换T时,CT得到的 是C相对于不同当前坐标系的变换,变换的动作顺序
由T的最前(最左)因子开始,以最前(最右)的因子结
束其变换.
举例


3.3.2齐次变换矩阵求逆
如果知道坐标系｛B｝相对｛A｝的描述 ，希望 得到｛ A｝相对（B｝的描述 ，这是个齐次变换 求逆问题.
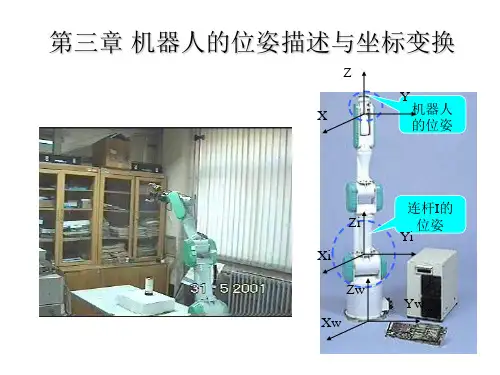
3.位姿描述和齐次变换


3.1刚体位姿描述和坐标变换
3.1.1位置的描述和坐标平移 1).位置的描述(位置矢量) 2).坐标平移
3.1.2姿态的描述和坐标旋转
1).姿态的描述(旋转矩阵) Pxyz=R· UVW P
由矢量分量的定义有

如果OUvw坐标系绕Ox轴转动α角,变换矩阵 Rx,α称为绕Ox轴旋转α角的旋转矩阵，即：
例:

并说明它所表示的运动(均指相对固定坐标 系而言)
3.3.3变换方程


{B}代表机座坐标系 （机座框）， {W}代表腕框, {T}代表工具框, {S}代表工作站框, {G}代表目标框. 对物体进行操作时,工具框 {T}相对目标框{G}的位姿 直接影响操作效果

与其他变换(位姿)之 间的关系类似于空间尺 寸链, 则是封闭环 。

《机器人技术基础》Chpt3

《机器人技术基础》Chpt3

12
机电工程学院
第三章 位姿和运动的描述

刚体运动与坐标变换: 旋转例子
Rac R(YA ,90) R( X B ,90) 0 1 0 0 0 1 1 0 0
RAC R( X A ,90) R(YB ,90) 0 0 1 1 0 0 0 1 0
物体坐标系映射到参考坐标系
I 33 pa 1 013
7
p ab p b
pb T 1 1 1
I T Trans( p ab ) 33 013
p ab
1
机电工程学院
第三章 位姿和运动的描述
位姿的描述需要3个参数，故 平面上的物体有三个自由度
4
机电工程学院
第三章 位姿和运动的描述

刚体的位形: 位姿的描述
空间 (三维) 情况 位置 (矢量表示) 姿态 (矩阵表示)
r11 r12 r13 i i ' i j ' i k ' j i ' j j ' j k ' 33 R [ri ' rj ' rk ' ] r r r 21 22 23 r31 r32 r33 k i ' k j ' k k '
虽九个元素，但有六个约束，故只有三个独立变量 (对应于三个角度)，因 此，姿态的描述需要三个参数。 p31 R 44 位姿的描述需要6个参数， g ( R, p) T 33 013 1 故空间中的物体有六个自由度
5
机电工程学院
第三章 位姿和运动的描述

机器人技术 数学基础-位姿描述与齐次变换

机器人技术 数学基础-位姿描述与齐次变换

nx ox ax Px
Fobject

ny

nz 0
oy oz 0
ay az 0
Py

Pz 1

二、刚体位姿的数学描述
2. 约束变量
由刚体（坐标系）在参考坐标系的齐次矩阵表达可知， 该矩阵有12个变量，但描述刚体位姿只需要6个变量（自由 度）就足够了，因此，齐次矩阵中12个变量之间并不是相互 独立的，而是有约束的，约束条件为：
(O')
y
Pxyz Px ix Py jy Pz kz Puvw Pxyz u
x
三、刚体位姿的坐标变换
② 当动坐标系ΣO´uvw绕O点回转时，求P点在固定坐标系Σoxyz 中的位置
Puvw Pu iu Pv jv Pw kw
已知：
z w
P点在ΣO´uvw中是不变的仍然成
a= x , b= y , c= z ，w为比例系数 w ww
显然，齐次坐标表达并不是唯一的，随
x
V

y z

x
y
z
w值的不同而不同。在计算机图学中，w
wT 作为通用比例因子，它可取任意正值，但
w
在机器人的运动分析中，总是取w=1 。
一、点、向量和坐标系的齐次表示
因此，习惯上用W＝1表示向量的长度，用W＝0表示向量的 方向，而且方向向量一般表示成单位向量的形式。形式如下：
机器人位姿描述基本术语
4) 手腕(Wrist)：位于执行器与手臂之间，具 有支撑和调整末端执行器姿态功能的机构。 操作臂的组成部分之一。
手Z 腕
X
5)手臂(Arm)：位于基座和手腕之间，由操作

第三章机器人的运动学

第三章机器人的运动学

B R 表示坐标系{B}相对于{A}的方位， R 描述坐标系{A}相对于{B}的方 A B A 1 A T A B 位，且 B R 和 A R 都是正交矩阵，两者互逆。即 A R B R B R
例3.1 若从基坐标系
矩阵为
({B})到手爪坐标系
({E})的旋转变换
。（1）画出两坐标系的相互方位关系（不考虑{E}的
分别代表了ox，oy和oz轴的无穷远
点，用它们分别表示这三个坐标轴的方向。另外，
坐标原点， 没有意义。
代表
注意：位置矢量 究竟是3×1的直角坐标还是4×1的齐次坐标，应 根据上下文而定。
二、齐次变换
齐次变换矩阵是4×4的矩阵，它的完整形式可以看成是由 四个子矩阵组成：
R33 P31 旋转变换 位置矢量 T f13 11 透视变换 比例变换
pBO 1

综合地表示了平移和旋转变换。 对平移变换
A B
A
R I 33 (3阶单位矩阵)

对旋转变换
pBO ＝0 3（3行1列零向量） 1

一、齐次坐标
一般来说，以N+1维矢量表达N维位置矢量的方法称为齐次 坐标表示法。 在三维直角坐标系中，一个点可以表示 为 次坐标就是 ，它的齐
p p
A B
A p B R p A pBO —坐标旋转和坐标平移的复合变换 可规定一个过渡坐标系{C},{C}的坐标原点与{B}的方位重合，而{C} 的方位与{A}的相同，则
C A B B
C A p BR p BR p C A A B B
原点位置）；（2）如果给出OE({E}系的原点）在{B}中的位置矢

位姿描述和齐次变换

位姿描述和齐次变换
zA
过渡矩阵—公式3-13
C
p
C B
R
B
p
A B
R
B
p
A
oA
再由3-11得到复合变换 xA
A p C p A pC0 BAR B p A pB0
zBp A Bo o
yA xB
3.1 一般变换实例
｛A，B｝初始位姿重合， ｛B｝相对于｛A｝的zA轴 转 30度，再沿xA轴移动10个单位、沿yA轴移动5个单 位，求位置矢量和旋转矩阵
这种方法用强氧化剂将L-山梨糖在4位的仲醇基氧化生成维C的重要前 体——2-酮基-L古龙酸（2-Keto-L-gulonic acid，简称2-KGA）。为了保护 山梨糖C6位伯醇基不被氧化，就须在酸性条件下先用丙酮处理L-山梨糖， 形成双丙酮衍生物后再进行氧化；氧化后还必须水解生成2-酮基-L-古龙酸 （不稳定，难分离出），再经转化而得维C。
莱氏法维生素C生产工艺过程
1．D-山梨醇的制备 山梨醇是葡萄糖在氢作还原剂，镍作催化剂的条件
下，将葡萄糖醛基还原成醇羟基而制得的。
工艺过程 将水加热至70~75℃，在不断搅拌下逐渐加 入葡萄糖至全溶，制成50%葡萄糖水溶液，再加入活性炭 于75℃，搅拌10min，滤去炭渣，然后用石灰乳液调节滤 液pH8.4，备用。当氢化釜内氢气纯度≥99.3%，压强 >0.04Mpa时可加入葡萄糖滤液，同时在触媒槽中添加活性 镍，利用糖液冲入釜内，以碱液调节pH为8.2~8.4，然后 通蒸汽并搅拌。当温度达到120~135℃时关蒸汽，并控制 釜温在150~155℃，压强在3.8~4.0MPa。取样化验合格后， 在0.2~0.3MPa压强下压料至沉淀缸静置沉淀，过滤除去催 化剂，滤液经离子交换树脂交换，活性炭处理，即得D-山 梨醇。

第3章 位姿描述和齐次变换

第3章 位姿描述和齐次变换
ZB ZA YB

P
AP
XB
OA
YA
A
参考坐标系{A}
机器人研究所
4
第1节 位置和姿态的表示
位置描述（Description of Position）
px A p p y pz
Ap
zA
{A}
p
A
p
：p点在坐标系{A}中的表示，
xA
oA
yA
也称作位置矢量。
图1 位置表示
齐次的，将其等价为齐次变换形式：
A A p B R | A pBo B p 0 0 0 | 1 1 1
A A B p B R p A pBo A
直角坐标
齐次坐标
等价于
p A BT
B
p
11
齐次变换
机器人研究所
22
第3节 齐次坐标变换
机器人研究所14坐标变换复合变换compositetransform机器人研究所15例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所16例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所17例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所18例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述3030086605303030050866坐标变换机器人研究所19例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述坐标变换机器人研究所20例21已知坐标系b的初始位姿与a重合首先b相对于坐标系a的zb0和旋转矩阵求它在坐标系a中的描述0866051211098050866坐标变换第第33节节齐次坐标变换齐次坐标变换旋转变换通式第三章位姿描述和齐次变换机器人研究所22齐次坐标变换齐次坐标和齐次变换坐标变换式中对于点是非齐次的将其等价为齐次变换形式

第三讲 位姿描述与齐次变换

第三讲 位姿描述与齐次变换

x
图2.4 旋转变换
(2.13)
注意：θ角旋转的正方向遵 循右手螺旋法则（如图2.4 所示）
Rot ( z, θ) =
(2.14)
三、齐次坐标变换
例3 ：U=7i+3j+2k,绕Z轴转90度后，再绕Y轴转90度。
0 − 1 1 0 R( z ,90) = 0 0 0 0 0 0 7 − 3 0 0 3 7 . ＝ 1 0 2 2 0 1 1 1
A
P= x
A
A A B
[
A
y
A
z 1 ， P= x
B
A BR A BT = 0 A
]
T B
[
B
y
z 1
]
T
而齐次变换公式和变换矩阵变为: 齐次变换公式和变换矩阵变为: 变为
P = T P,
B
PB 0 1
三、齐次坐标变换
2.平移齐次坐标变换 2.平移齐次坐标变换
{A}分别沿{B}的X、Y、Z坐标轴平移a、b、c距 {A} 离的平移齐次变换矩阵写为：
1 0 Trans ( a , b , c ) = 0 0 0 1 0 0 0 0 1 0 a b c 1
用非零常数乘以变换矩阵的每个元素，不改变特性。
三、齐次坐标变换
• 例2：求矢量2i+3j+2k被矢量4i-3j+7k平移得到的 新矢量。
1 0 0 0 0 1 0 0 0 0 1 0 − 3 7 1 4 2 3 2 1 6 0 9 1
＝
0
y
起始点u和终点v如图2.5所示。如将v点再绕y轴 旋转90°得到w。用式（2.13）变换得到 0 0 -1 0 0 1 0 0 1 0 0 0 0 0 0 1 -3 7 2 1

第三章齐次变换

第三章齐次变换

0
0
0 1
解 F n eT ： w( r d x ,d a y ,d z ) n F os lT d ( r 9 ,0 ,5 a ) F o n ld s
第17页，共52页。
2.5齐次变换矩阵－绕轴纯旋转的变换
为了简化绕轴旋转的推导，首先假设该坐标系位于参考坐标系的原点。然后推广 到其他的旋转以及旋转的组合。
系x轴旋转90°。求旋转后该点相对于参考坐标系的坐标。
第22页，共52页。
2.5齐次变换矩阵－复合变换
例1：在动坐标中有一固定点 P'uovw 1231 ，T相对固定参考
坐标系 Ox做yz如下运动：① R（x, 90°）；② R(z, 90°)；③
R(y,90°)。求点
在固定P参o'u考vw坐标系
0 1 0 dyny oy ay Pyny oy ay Pydy
0 0
0 0
1 0
d1z
n 0z
oz 0
az 0
P 1z
n 0z
oz 0
az 0
Pz 1dz
第15页，共52页。
2.5齐次变换矩阵－纯平移变换
1 0 0 dx nx ox ax P x nx ox ax P xdx
F ne w0 0 0
x
o
y
第19页，共52页。
2.5齐次变换矩阵－绕轴纯旋转的变换
Px 1 0
0 Pn
Py0 cos sinPo
Pz 0 sin cos Pa
Pxy z Ro (x,t)Pnoa
1 0 0
则Ro(tx,)0 cos sin 0 sin cos
第20页，共52页。
2.5齐次变换矩阵－绕轴纯旋转的变换

3位姿变换Trans-Matrix

3位姿变换Trans-Matrix

4、绕二个坐标轴旋转的变换矩阵
相对动坐标系的变换顺序： (1)i 系先绕自身的 z 轴转 角，得 m 系。 (2)再绕新m系的x轴转角，得变 换后的j系。 zj α zi yj ym α θ
yi
θ 总变换矩阵：R R( z, ) R( x, )
xi
xm ,xj
相对动坐标系的变换
zi zn zj θ α yj θ α yn yi
c s 0 s c 0 0 cb 0 0 1 sb 0 sb 1 0 0 cg 1 0 0 cb 0 sg 0 sg cg
c cb s cb sb
csb sg s cg ssb sg c cg cb sg
联立两式得
csb sg s cg ssb sg c cg cb sg
csb cg s sg ssb cg c sg cb cg
2 2 cos b r11 21
于是得
b A tan 2(r , r 2 r 2 ) 31 11 21 A tan 2(r21, r11) g A tan 2(r , r ) 32 33
p xb w
u
yb
ob
v
点p在基坐标系和刚体坐 标系的位置矢量分别为
x x y z u xb v w
x0 o x y xb
坐标变换
x与xb之间的变换关系为
x x0 un vo wa
从坐标xb到基坐标x的一般变换关系式
x x y 齐次坐标： x y x z z 1
u xb v w
u v 齐次坐标： xb w 1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

zB zA yB OB OA xA 30ox
B
zA zB OA yA OB 30o
30o
yB
yA
(10,5,0)
xA 30o xB
所以有：
cos300 A 0 0 R R ( z , 30 ) sin 30 B 0
A
sin 300 cos300 0
0 0.866 0.5 0 0 0.5 0.866 0 1 0 1 0
6.矩阵的运算 （1）矩阵的加法：两同型矩阵的对应元素相加。
（2）矩阵与数相乘：该数与矩阵各元素相乘。
（3）矩阵与矩阵相乘：
（4） 矩阵的转置：把矩阵的行换成同序数的列，记为
7. 矩阵的逆（逆矩阵）
8. 分块矩阵：分块后的矩阵与普通矩阵的运算相同。
9. 正交矩阵：如果 如果
，则A为正交矩阵。它满足： 是正交矩阵，则
四、矢量的叉积（矢量积或叉乘积）
其中矢量c的模为:
叉乘积
其中θ是a和b间小于等于1800的夹角，若将a按右手法则绕c 转θ角至b，右手拇指指向为c的正方向（如上图所示），c与a、b 两者垂直。 若a和b用分量的形式表示为: 则
a和b的点乘为：
将点乘和叉乘应用于右手笛卡尔坐标系的单位矢量i，j，k，有：
和
都是正交矩阵，因此满足
由
与
互逆，可得
若把
写成行向量的形式
，则其中 满足六个约束条件
每一个元素都是一个列向量。容易得出 （称正交条件）：
旋转矩阵的几何意义：旋转矩阵在几何上表示了发生相互旋 转的两坐标系各主轴之间的相互方位关系。
因此写出三个基本的旋转矩阵，即分别绕x、y和z轴转θ角的旋转 矩阵：
原点位置）；（2）如果给出OE({E}系的原点）在{B}中的位置矢
量为（1，2，2），画出两坐标系的相对位姿关系；（3）求a，
b，c的值。 解：
xB xE yE zE
zB zE xE yB xB yE
zB
(1,2,2)
zE xE yB
(1)
yB
zB
(2)
xB yE
(3) a=0，b=1，c=0
三、一般变换
A B PBO P 1 1
A
A B A P B R P PBO
11
简写成 综合地表示了平移和旋转变换。
3.3.1 齐次坐标
一般来说，以N+1维矢量表达N维位置矢量的方法称为齐次 坐标表示法。
在三维直角坐标系中，一个点可以表示 为
次坐标就是
，它的齐
PBO
10 5 0
A B A 最后得： P B R P PBO
A
9.098 12 . 562 0
3.3 齐次坐标与齐次变换
复合变换式 可以表示成等价的齐次变换式。
A A P B R 1 0
第三章 位姿描述和齐次变换
3.1 相关知识回顾
一、行列式和矩阵 1. 行列式按照行（或列）展开法则：行列式等于它的任意一行 （或列）各元素与其对应的代数余子式乘积之和。
2.行矩阵
3.列矩阵
4.矩阵相等：两同型矩阵（行数和列数都相等）对应元素相等。
5.单位矩阵：主对角线元素为1，其它所 有的元素都为0的方阵。
3.2 位姿描述与坐标变换
3.2.1 刚体位置姿态（位姿）描述
a) 位置的描述
采用直角坐标描述点的位置，因此，刚体F的位置描述，即 OB点在{A}中描述可用一个3×1的列矢量 （位置矢量）表示，即
其中Px、Py和Pz是点OB在{A}系中的三个坐标分量。
b) 姿态（方位）的描述 采用旋转矩阵来表示刚体姿态（方位） ，即由{B}系的三个 单位主矢量相对于坐标系{A}的方向余弦组成： xB yB zB
，即满足Px=ωPx/ω，Py=ωPy/ω，
行列式和矩阵的区别：矩阵是按一定方式排成的数表；行列式是
一个数。
二、直角坐标系
若基矢量相互正交，即它们在原点o处两 两相交成直角，则它们构成直角坐标系或笛卡 儿坐标系。 若按右手法则绕oz轴转900可以使ox轴转向 oy轴，则称为右手坐标系；按左手法则形成的 坐标系称左手坐标系。
斜角坐标系
（a）右手坐标系
本课程使用右手坐标系。
（b）左手坐标系
三、矢量的点积（内乘积或标量积）
其中θ是a和b两矢量间的夹角，如图所示。
令b=i （i为b方向上的单位矢量），则
标量积
换句话说：一个矢量在另一个矢量上的投影等于该矢量与另一矢 量方向上单位矢量的点积。 再令a=j （j 为a方向上的单位矢量），则
即两矢量方向上单位矢量的点乘等于两矢量夹角的余弦。
一般的情况：坐标系{B}的原点既不与{A}重合，方位也不相同。
{C}系与｛Ｂ｝系原点重合， 但方位不同，所以得
{C}系与｛A｝系原点不重合， 但方位相同，所以得 和
A
A PCO PBO
进而有
例3.2 已知坐标系{B}初始位姿与{A}重合，首先{B}相对{A}的zA轴 转30°，再沿{A}的xA轴移动10个单位，并沿{A}的yA轴移动5个单 位。求位置矢量 解： 和旋转矩阵 。若 ,求 。
xA yA zA
其中：cos cos(xB , x A ) 既表示了刚体F在{A}系中的方位，也描述了{B}系在{A}系中
的姿态。
3.2.2 坐标变换
一、坐标平移
如图所示，坐标系{B}与 {A}方向相同，但原点不重合。
坐标平移
此式称为平移方程。其中
是B系中的原点在A系中的表示。
二、坐标旋转
z' θ z y' θ y
x θ x’
x’ x y z y’ z’ x y x’ y’ z’ x y z
z' θ z
z z'
y' y
x θ x’
x’ y’
y' θ y标系
矩阵为
({B})到手爪坐标系
({E})的旋转变换
。（1）画出两坐标系的相互方位关系（不考虑{E}的
坐标旋转
如图所示，{B}与{A}有共同的坐标原点，但方位不同。令
和
分别是{A}和{B}中的单位主矢量，点P 在两
坐标系中各坐标轴上的坐标分量分别为：
和
所以有 利用点乘的性质和上式共同求解得
将
代入上面三式中并写成矩阵形式得
上式简写为：
此式称为坐标旋转方程。其中旋转矩阵 表示了坐标系{B}相
对于{A}的方位，正好与刚体姿态的描述相同。同理也可得