机器人学_第二讲 齐次变换矩阵

相机坐标系到机械臂末端坐标系的齐次变换矩阵是机器视觉和工业机器人领域中一个非常重要的概念。

对于工业领域的自动化生产，机械臂和相机之间的精确配准是至关重要的，而齐次变换矩阵正是用来描述相机坐标系到机械臂末端坐标系之间的关系的。

本篇文章将深入探讨相机坐标系到机械臂末端坐标系的齐次变换矩阵的计算方法，并且将详细介绍该计算方法的原理和实际应用。

一、齐次变换矩阵的概念和基本原理齐次变换矩阵是一种用来描述坐标系之间关系的数学工具，它可以将一个坐标系中的点映射到另一个坐标系中去。

在工业机器人和机器视觉系统中，我们常常需要将相机坐标系中的点映射到机械臂末端坐标系中，这就需要使用到齐次变换矩阵。

齐次变换矩阵的基本形式如下所示：\[ T = \begin{bmatrix} R & t \\ 0 & 1 \end{bmatrix} \]其中，\[R\]为旋转矩阵，\[t\]为平移向量。

齐次变换矩阵可以将一个点的坐标\[P\]从相机坐标系变换到机械臂末端坐标系：\[ P' = T \times P \]二、计算相机坐标系到机械臂末端坐标系的齐次变换矩阵计算相机坐标系到机械臂末端坐标系的齐次变换矩阵需要以下步骤：1. 确定相机坐标系和机械臂末端坐标系的原点需要确定相机坐标系和机械臂末端坐标系的原点位置。

这两个坐标系的原点通常是相机的光学中心和机械臂末端执行器的中心点。

确定了原点位置之后，我们可以将相机坐标系和机械臂末端坐标系的坐标系原点重合。

2. 计算旋转矩阵接下来，需要计算相机坐标系到机械臂末端坐标系的旋转矩阵。

旋转矩阵描述了两个坐标系之间的旋转关系。

在实际应用中，可以通过标定相机和机械臂的姿态来获取旋转矩阵。

3. 计算平移向量除了旋转矩阵之外，还需要计算相机坐标系到机械臂末端坐标系的平移向量。

平移向量描述了两个坐标系之间的平移关系。

平移向量可以通过相机和机械臂的空间位置信息来计算得到。

4. 组合旋转矩阵和平移向量将计算得到的旋转矩阵和平移向量组合在一起，就得到了相机坐标系到机械臂末端坐标系的齐次变换矩阵。

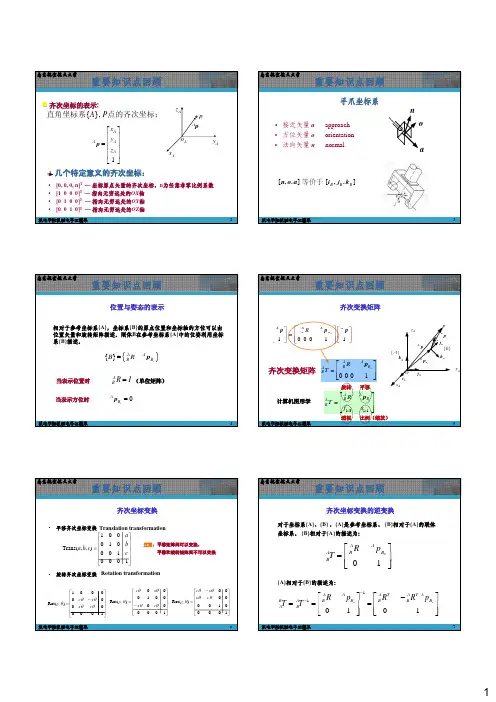
举例说明运用齐次变换矩阵求解机器人正运动学的方法齐次变换矩阵用于描述刚体在空间中的位姿（位置和方向）。

在机器人正运动学问题中，运用齐次变换矩阵可以求解机器人末端执行器的位姿。

我们以一个简单的2R（两个旋转关节）机械臂为例进行说明。

假设2R机械臂有两个关节q1和q2，臂长分别为L1和L2。

我们的目标是求解两个关节角度q1和q2下，末端执行器的位置坐标(x, y)和方向theta。

首先，我们需确定两个坐标系。

通常将基坐标系（frame0）放在第一个关节处，frame1放在第二个关节处，frame2放在末端执行器处。

然后，我们需要分别计算从frame0到frame1的齐次变换矩阵T01和从frame1到frame2的齐次变换矩阵T12。

T01表示frame1相对于frame0的位姿，其旋转角度为q1，平移距离为L1。

矩阵形式如下：```T01 = | cos(q1) -sin(q1) 0 L1*cos(q1) || sin(q1) cos(q1) 0 L1*sin(q1) || 0 0 1 0 || 0 0 0 1 |```同理，T12表示frame2相对于frame1的位姿，其旋转角度为q2，平移距离为L2。

矩阵形式如下：```T12 = | cos(q2) -sin(q2) 0 L2*cos(q2) || sin(q2) cos(q2) 0 L2*sin(q2) || 0 0 1 0 || 0 0 0 1 |```接下来，我们需要计算从frame0到frame2的齐次变换矩阵T02。

通过矩阵乘法，我们可以得到：```T02 = T01 * T12```最后，我们从T02矩阵中提取机器人末端执行器的位置和方向。

位置坐标(x, y)就是T02矩阵中的平移部分，即：```x = T02[0][3]y = T02[1][3]```方向theta可以通过以下公式计算：```theta = atan2(T02[1][0], T02[0][0])```所以，通过齐次变换矩阵，我们可以求解出机器人末端执行器的位置和方向，从而解决2R机械臂的正运动学问题。

举例说明运用齐次变换矩阵求解机器人正运动学的方法运用齐次变换矩阵求解机器人正运动学是机器人学中重要的一个应用。

在机器人学中，正运动学问题是指根据机器人各关节的运动参数，求解机器人末端执行器的位置和姿态。

齐次变换矩阵是一种用来描述从一个坐标系到另一个坐标系的变换关系的方法，它可以将平移和旋转变换统一起来，因此非常适用于机器人的运动学描述。

下面我们以一个简单的二自由度机械臂为例，详细说明如何运用齐次变换矩阵求解机器人正运动学。

1.机器人几何参数的定义我们首先需要定义机器人的几何参数，包括各关节的长度、原点位置和旋转轴方向等。

假设我们的机器人臂长分别为L1和L2，关节1的旋转轴在z轴上，关节2相对于关节1的旋转轴在y轴上。

2.齐次变换矩阵的构建根据机器人的几何参数，我们可以构建各关节相对于前一关节的齐次变换矩阵。

对于本例中的二自由度机械臂，我们需要构建两个齐次变换矩阵，分别表示关节1和关节2相对于机器人基座的变换关系。

假设关节1的变换矩阵为T1，关节2的变换矩阵为T2，机器人基座的变换矩阵为Tbase。

根据机器人几何参数的定义，我们可以得到如下变换矩阵的表达式：T1 = [cos(θ1) -sin(θ1) 0 L1*cos(θ1)sin(θ1) cos(θ1) 0 L1*sin(θ1)00100001]T2 = [cos(θ2) 0 sin(θ2) L2*cos(θ2)0100-sin(θ2) 0 cos(θ2) L2*sin(θ2)0001]Tbase = [1 0 0 001000 0 1 d_base0001]其中θ1和θ2分别表示关节1和关节2的旋转角度，d_base表示机器人基座的高度。

3.机器人末端执行器的正运动学求解对于机器人末端执行器的正运动学问题，我们需要根据机器人各关节的运动参数，如各关节的旋转角度，通过乘法计算得到末端执行器的位置和姿态。

具体过程如下：a)首先，将各关节的变换矩阵相乘，得到机器人末端执行器相对于基座的变换矩阵。

举例说明运用齐次变换矩阵求解机器人正运动学的方法机器人正运动学是指根据机器人关节角度，求出机器人末端执行器的位置和姿态。

运用齐次变换矩阵的方法可以方便地求解机器人正运动学。

齐次变换矩阵是一种描述机器人移动和旋转的数学工具，它能够将机器人的位置和姿态用一个矩阵表示出来。

在机器人正运动学中，我们需要根据机器人各个关节的角度来求出机器人的位置和姿态。

假设机器人有n个关节，每个关节的旋转角度分别为θ1,θ2,...,θn。

我们可以用齐次变换矩阵来表示机器人每个关节的旋转和移动。

假设第i个关节的齐次变换矩阵为Ti，则Ti = [cosθi -sinθi 0 ai;sinθi cosθi 0 bi;0 0 1 ci;0 0 0 1];其中ai, bi, ci分别表示第i个关节的位置坐标，θi表示第i个关节的旋转角度。

机器人的末端执行器的位置和姿态可以通过将所有关节的齐次变换矩阵相乘得到。

即T0n = T1 * T2 * ... * Tn;其中T0n表示机器人的末端执行器的齐次变换矩阵。

通过分析T0n的各个元素，我们可以得到机器人末端执行器的位置和姿态信息。

举例说明，假设有一个二自由度机器人，其第一个关节的旋转角度为θ1，第二个关节的旋转角度为θ2。

假设机器人的关节长度均为1，且第二个关节相对于第一个关节的位置偏移为1。

则第一个关节的齐次变换矩阵为T1 = [cosθ1 -sinθ1 0 0;sinθ1 cosθ1 0 0;0 0 1 0;0 0 0 1];第二个关节相对于第一个关节的位置偏移为1，因此第二个关节的位置坐标为(1,0,0)。

其齐次变换矩阵为T2 = [cosθ2 -sinθ2 0 1;sinθ2 cosθ2 0 0;0 0 1 0;0 0 0 1];将两个齐次变换矩阵相乘得到机器人的末端执行器的齐次变换矩阵为T0n = T1 * T2= [cosθ1cosθ2-sinθ1sinθ2 -cosθ1sinθ2-sinθ1cosθ2 0 cosθ1;sinθ1cosθ2+cosθ1sinθ2 -sinθ1sinθ2+cosθ1cosθ2 0 sinθ1;0 0 1 0;0 0 01];通过分析T0n的各个元素，我们可以得到机器人末端执行器的位置和姿态信息。