一、最大值和最小值定理
- 格式:pdf
- 大小:224.42 KB
- 文档页数:2

最大最小值定理最大最小值定理又称最小-最大定理,是指在约束条件下,某一约束优化问题的最优解是所有解的最大值或最小值。
其主要分为三种情况:1. 最小值原理:某一约束条件下的最优解是目标函数的最小值;2. 最大值原理:某一约束条件下的最优解是目标函数的最大值;3. 最小化最大值原理:存在某一约束条件下的最优解,它是满足某一约束条件下剩余约束函数的最大值最小化。
最大最小值定理是非常常用的一种优化算法,用于优化问题的最优解。
它包括构造约束条件、确定目标函数,以及实施算法求解等步骤,可以帮助我们快速求解给定优化问题的最优解。
有时候,由于约束条件的存在,我们无法直接求解优化问题的最优解。
此时,可以通过最大最小值定理来求解,即在约束条件下求解最优解,那么最优解就可以由于最大最小值定理而得出。
同时也可以将最大最小值定理和其他优化算法结合起来使用,从而加快求解速度,提高求解精度。
此外,最大最小值定理还可用于多维优化问题的求解。
因此,最大最小值定理是解决优化问题的重要方法,为优化问题的求解提供了有效的理论支持。
使用最大最小值定理来求解优化问题时,在确定约束条件、目标函数等步骤完成后,需要考虑算法复杂度、收敛速率等问题,以便选择合适的方法。
例如,可以考虑使用梯度下降法、遗传算法、变分法等方法来求解最优解。
此外,还可以对最大最小值定理的约束条件和目标函数进行有效的优化,以便提高求解精度。
为此,可以利用不同的方法,如凸优化技术、多约束技术、约束优化技术等,来优化约束条件和目标函数。
总之,最大最小值定理是一个非常有用的解决优化问题的算法,它能够帮助我们快速求解复杂优化问题,可以有效提高求解精度。

基本不等式最大值最小值公式不等式是数学中的一种基本概念。
在实际生活和工作中,我们会遇到各种各样的不等式问题。
投资的收益率大于某个固定值,或者某个物品的价格必须低于定价等等。
为了解决这些问题,我们需要用到不等式的理论和技巧。
不等式的最大值和最小值是非常重要的概念。
其指的是在给定条件下,不等式所能达到的最大和最小的值。
基本不等式就是一种常见的最大最小值公式。
基本不等式是指对于任意的正实数 a_1, a_2, ..., a_n,有如下的不等式关系:\frac{a_1+a_2+...+a_n}{n}\geq \sqrt[n]{a_1a_2\cdot\cdot\cdot a_n}\geq\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdot\cdot\cdot+\frac{1}{a_n}}左边的式子称为算术平均数和几何平均数不等式,右边的式子称为调和平均数不等式。
这两个不等式可以统称为基本不等式。
基本不等式的原理是利用平均值不等式和相应的积分不等式证明的。
平均值不等式指的是对于一组数,算术平均数大于等于几何平均数,大于等于调和平均数。
即:\frac{a_1+a_2+\cdot\cdot\cdot+a_n}{n}\geq\sqrt[n]{a_1a_2\cdot\cdot\cdota_n}\geq\frac{n}{\frac{1}{a_1}+\frac{1}{a_2}+\cdot\cdot\cdot+\frac{1}{a_n}}这是数学中的一个基本定理,其应用范围非常广泛。
而基本不等式是平均值不等式的一种特例,其应用范围也同样广泛。
下面我们来看一下基本不等式的具体应用。
基本不等式广泛应用于数学竞赛等数学问题的解决中。
在一些竞赛题目中,基本不等式常常被用来证明一些不等式关系,或者推导最大最小值等问题。
基本不等式还可以应用于物理、化学等领域的一些问题。
在物理和化学中,我们也经常会遇到一些关于最大最小值的问题。

最值定理及应用举最值定理是高等数学中的重要概念,它有两种形式:最大最小值存在定理和最值原理。
最值定理是研究函数在闭区间上的最值性质的定理,对于函数的最大值和最小值的存在性具有重要的指导作用。
在实际问题中,我们经常需要确定函数在一定范围内的最大值和最小值,最值定理能够帮助我们简化问题的求解过程。
首先,我们来介绍最大最小值存在定理。
对于一个定义在闭区间[a, b]上的连续函数f(x),最值存在定理告诉我们,f(x)在[a, b]上必定有最大值和最小值,并且这两个最值必定是在[a, b]的端点处或者在[a, b]的内部点处取到的。
证明最大最小值存在定理的方法通常使用反证法。
假设在[a, b]上不存在最大值,即对于任意的x∈[a, b],都有f(x)<M,其中M是一个实数。
由于f(x)是连续函数,根据介值定理,我们可以得到存在一个点x0∈[a, b],使得f(x0)=M,这与假设矛盾。
所以假设不成立,即[a, b]上必定存在最大值。
同理,可证明最小值也存在。
接下来,我们来介绍最值原理。
对于一个定义在开区间(a, b)上的函数f(x),如果f(x)在(a, b)上取得了最大值或者最小值,那么这个最值只能是在(a, b)的端点处取到的。
最值原理的证明同样可以使用反证法。
假设f(x)在(a, b)的内部点处取得最大值或者最小值,即存在c∈(a, b),使得f(c)是f(x)在(a, b)上的最大值或最小值。
由于f(x)在(a, b)上连续,根据介值定理,我们可以找到一个(a, b)内的点d,使得f(d)在f(c)的右侧或左侧,与f(c)是最大值或最小值的假设矛盾。
因此,我们可以得出结论,最值只能出现在(a, b)的端点处。
最值定理在实际问题中有着广泛的应用。
一个常见的应用是在优化问题中,我们需要找到一个函数在一定范围内的最大值或最小值。
最值定理告诉我们,只需要在闭区间的端点和内部点处计算函数值,然后从这些值中找出最大值或最小值即可。

函数极限连续重要概念公式定理函数的极限、连续是微积分中非常重要的概念。
它们是帮助我们研究函数性质、计算导数和积分的基础。
下面我们将详细介绍函数极限和连续的概念、常用公式和定理。
一、函数极限函数的极限是指当自变量趋向一些特定值时,函数的取值是否趋于确定的结果。
极限表示函数在其中一点的趋势和变化情况。
函数极限的概念可以分为以下几个层次:1.无穷极限当自变量趋向无穷大或无穷小时,函数的极限称为无穷极限。
常见的无穷极限有以下几种形式:- 当$x\rightarrow+\infty$时,$\lim_{x\rightarrow+\infty}f(x)=L$,表示当$x$趋向正无穷时,函数$f(x)$的极限为$L$。
- 当$x\rightarrow-\infty$时,$\lim_{x\rightarrow-\infty}f(x)=L$,表示当$x$趋向负无穷时,函数$f(x)$的极限为$L$。
- 当$x\rightarrow+\infty$时,$\lim_{x\rightarrow+\infty}f(x)=+\infty$,表示当$x$趋向正无穷时,函数$f(x)$的极限为正无穷。
- 当$x\rightarrow-\infty$时,$\lim_{x\rightarrow-\infty}f(x)=-\infty$,表示当$x$趋向负无穷时,函数$f(x)$的极限为负无穷。
2.有限极限当自变量趋向一些有限值时,函数的极限称为有限极限。
常见的有限极限有以下形式:- 当$x\rightarrow a$时,$\lim_{x\rightarrow a}f(x)=L$,表示当$x$趋向$a$时,函数$f(x)$的极限为$L$。
3.间断点函数在一些点上不具有有限的极限时,称该点为函数的间断点。
常见的间断点有以下几种类型:- 第一类间断点:当$x\rightarrow a$时,函数极限不存在且左右极限存在,即$\lim_{x\rightarrow a^-}f(x)$和$\lim_{x\rightarrowa^+}f(x)$存在,但不相等。


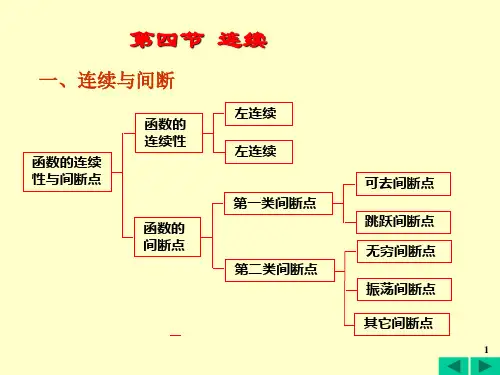


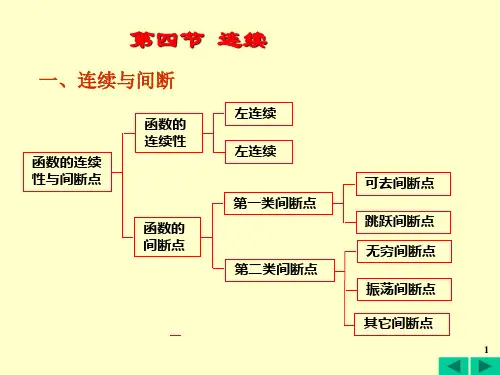

《微积分》复习大纲第二章、极限与连续第一节、数列的极限教学目的和要求:1、通过割圆术和截杖问题的计算实例引入数列极限的概念,从中领会极限的基本思想。
2、使学生了解的极限定义和性质,并通过例题学会如何处理和解决相应的数学问题。
重点:数列极限的概念教学过程:一、问题的提出1、刘徽的割圆术2、截杖问题二、数列极限的定义注:1、数列是否有极限,与其前面的有限项无关•而与从某项以后的变化情况有关,因此改变一个数列的有限项的值或去掉或添加有限项,均不改变{ X n} 的收敛与发散性;2、在证明数列有极限时,不一定要找到最小的正整数N,只要证明其存在即可.显然,如果证明了存在符合要求的正整数N,那么这种就有无穷多个.3、数列极限的定义未给出求极限的方法.第二节、函数的极限教学目的和要求:1、理解函数极限的概念,了解;-X ,;定义。
2、使学生了解的函数极限性质重点:函数极限的概念教学过程:一、函数极限的定义1、自变量趋于无穷大时函数的极限注:讨论当自变量X的绝对值|X无限增大(X r ,X r 一,X))时,函数f (X)无限趋近于一个常数A的情形.2、自变量趋于有限值时函数的极限注:研究自变量x无限趋近于一个常数x o,(x— x0,x_. x0,x_. \7),函数f (x) 无限趋近于一个常数A的情形.三、例题分析例1证明lim叱=0.x注:1本题考察用定义验证函数极限的一般过程2、若|im f x =c,则直线y = c是函数y= f x的图形的水平渐近线。
例2:证明lim c =c ( c为常数).X—注:常数在任一点的极限是常数。
例3:证明lim x = x0.X—sxo例4:证明lim匸1 =2.一x—1注:函数在某一点是否有极限,与该点是否有定义无关。
\+1, x c0例5:设f (x)=彳0, x =0证验当X T0时,f (x )的极限不存在.x2 -1, x 0注:函数f X当x > X。
最大值原理和极值原理
最大值原理和极值原理是数学分析中的基本概念,它们描述了函数在一定条件下取得最大值或极值的规律。
最大值原理指出:如果函数在某个区间内连续且有定义,那么它在该区间内一定存在最大值和最小值。
也就是说,如果用y=f(x)来
表示该函数,那么必定存在一些x值,使得f(x)的值最大或最小。
这些值称为该函数的最大值和最小值。
极值原理则是最大值原理的特例,它指出:如果函数在某个区间内连续且有定义,并且在该区间内有一个点x0,使得f(x0)的值是该区间内的最大值或最小值,那么x0就是该函数的极值点。
极值点分
为两种,一种是极大值点,即当x在x0的左侧取值时,f(x)的值比
f(x0)小;另一种是极小值点,即当x在x0的左侧取值时,f(x)的值比f(x0)大。
最大值原理和极值原理是数学中的基础定理,它们在各种应用中都有广泛的应用,例如在优化问题、微积分中,都需要用到这两个原理。
掌握这两个原理对于学习数学和物理等相关学科都具有重要意义。
- 1 -。
海莱第一定理海莱第一定理是数学中的一个重要定理,它是数学分析中的基本定理之一。
该定理在数学分析中具有重要的应用价值,对于理解和应用数学分析的知识具有重要意义。
海莱第一定理是关于连续函数的定理,它表明一个连续函数在闭区间上达到最大值和最小值。
具体而言,如果一个函数在闭区间上连续,那么它一定在该闭区间上取得最大值和最小值。
这个定理的证明过程较为复杂,这里不做详细阐述。
但是,我们可以通过一个例子来理解这个定理的应用。
假设我们有一个连续函数f(x),它在闭区间[0, 1]上连续。
我们想要求出该函数在该闭区间上的最大值和最小值。
根据海莱第一定理,我们知道f(x)在闭区间[0, 1]上一定存在最大值和最小值。
为了找到这些值,我们可以使用一种方法,即通过计算函数在闭区间的边界点和极值点处的函数值,找出最大值和最小值。
我们计算f(x)在闭区间的边界点处的函数值。
在这个例子中,边界点为0和1。
我们计算f(0)和f(1)的值,然后比较它们的大小。
假设f(0) < f(1),那么f(x)在闭区间[0, 1]上的最大值就是f(1),最小值就是f(0)。
我们计算f(x)在闭区间的极值点处的函数值。
这些极值点可以通过求解f'(x)=0得到。
我们求解f'(x)=0的解,得到极值点x0。
然后计算f(x0)的值,与之前求得的最大值和最小值进行比较。
通过上述方法,我们可以找到f(x)在闭区间[0, 1]上的最大值和最小值。
这个例子说明了海莱第一定理在实际问题中的应用。
除了上述例子外,海莱第一定理还可以应用于其他数学问题中。
例如,在优化问题中,我们可以利用该定理来求解最优解。
在微积分中,该定理也有着重要的应用,可以帮助我们求解函数的极值点。
总结来说,海莱第一定理是数学分析中一个重要的定理,它表明一个连续函数在闭区间上一定存在最大值和最小值。
这个定理在实际问题中有着广泛的应用,可以帮助我们解决各种数学问题。
通过理解和应用海莱第一定理,我们可以更好地掌握数学分析的知识,提高数学问题的解决能力。