等量关系式定义

等量关系式定义:等量关系式就是表达数量间得相等关系得式子,如果要求用方程解答时,就需找出题中得等量关系,从而列出等量关系式。

常见关系式:减法等量关系式:被减数=减数+差差=被减数-减数减数=被减数-差加法等量关系式:加数=与-另一个加数与=加数+加数乘法等量关系式:积=因数×因数因数=积÷另一个因数除法等量关系式:被除数=除数×商商=被除数÷除数除数=被除数倍数等量关系式:每份数×份数=总数总数÷每份数=份数总数÷份数=每份数一、译式法将题目中得关键性语句翻译成等量关系。

(一)从关键语句中寻找等量关系。

1、关键句就是“求与”句型得、例:先锋水果店运来苹果与梨共720千克,其中苹果就是270。

运来得梨有多少千克?2、关键句就是“相差关系”句型。

关键词:比一个数多几,比一个数少几,例:小张买苹果用去7、4元,比买橘子多用0、6元,每千克橘子多少元?3、关键句就是“倍数关系”句型。

饲养场共养2400只母鸡,母鸡只数就是公鸡只数得2倍,公鸡养了多少只?4、有两个关键句,既有“倍数”关系,又有“求与”或者“相差”关系。

(必考考点) 一般把“与差”关系作为全题得等量关系式,倍数关系作为两个未知量之间得关系,用来设未知量。

(1倍数设为x ,几倍数设为几x 。

)如果只有与差关系得话,一般把求与关系作为全题得等量关系式,相差关系作为两个未知量之间得关系。

(把较小数设为x ,则较大数为x +a 。

)例:果园里共种240棵果树,其中桃树就是梨树得2倍,这两种树各有多少棵?例:河里有鹅鸭若干只,其中鸭得只数就是鹅得只数得4倍。

又知鸭比鹅多27只,鹅与鸭各多少只?例:后街粮店共运来大米986包,上午比下午多运14包,上午与下午各运多少包?二)没有关键句,找关键字上,寻找等量关系式。

“一共”、“还剩”例:网球场一共有1428个网球,每筒装5个,还剩3个。

这题怎么写,用方程解答列出等量关系式,正确采纳.本文讲述了如何用方程解答列出等量关系式，给出了一些有关求解等量关系式的实例，以便读者有所启发，学会使用方程解答列出等量关系式。

方程解答是一种用来查找并列出等量关系式的简单方法。

它可以帮助人们求解简单和复杂的数学问题。

在方程解答中，等量关系式指的是两个定义的方程的解之间的等量关系。

这通常用于科学计算和数学问题中，可以大大简化解决问题的方式。

方程解答的步骤包括：（一）定义问题：先找出问题的主要元素，确定相应的变量。

（二）解答问题：利用等量关系式，并将变量用简单因式表达；了解变量间联系，并将它们纳入解答步骤。

（三）求解问题：计算变量之间的等量关系。

这一步通常使用代数或数学方法，例如因式分解、组合等来计算变量之间的等量关系。

（四）校验答案：为了确认所得解决方式是否正确，通常需要使用比较法校验答案的准确性。

下面举个例子，说明方程解答列出等量关系式的解决方法。

例如，求解一个数学问题，要求x和y之间的等量关系式，即定义x + y = z。

我们可以一步步来解决问题。

（一）定义问题：我们需要考虑x和y两个变量，以及它们之间的等量关系式，即x + y = z。

（二）解答问题：我们可以将等量关系式表示为：z = x + y。

（三）求解问题：接着我们可以使用因式分解法，将等量关系式分解为：x = z - y 且 y = z - x。

因此，我们可以得到x和y的等量关系式：x = z - y 且 y = z - x。

（四）校验答案：我们可以将这些等量关系式放入等量关系式：z = x + y，用实际数字测试一下，看看结果是否正确。

从上面的例子中可以看出，方程解答是一种有效的查找和列出等量关系式的解决方法。

它可以帮助我们解决复杂的问题，避免使用大量的数学计算量。

如何找等量关系式、列方程什么是等量关系式：数量之间的相等的关系式叫做等量关系式。

找等量关系式的原则：一般来说，等量关系式能列成加法的，就不列成减法的；能列成乘法的就不列成除法的。

列方程：对应着等量关系式，把数量一个一个代进去列出方程，把未知数用“X”替代（一般情况可将问题设为未知数）。

一、根据常用的数量关系确定等量关系。

单价×数量＝总价速度×时间＝路程单价= 速度=数量= 时间=工作效率×工作时间=工作总量单产量×数量＝总产量工作效率= 单产量=工作时间= 数量=1、某款式的服装，零售价为36元1套，现有216元，问一共可以买多少套衣服？等量关系式：方程：2、养鸡场每天出产鲜蛋400千克，7天一共出产鲜蛋多少千克？等量关系式：变形：方程：二、根据公式确定等量关系。

长×宽＝长方形面积（长+宽）×2＝长方形的周长边长×4＝正方形的周长1、一个长方形的面积是20平方米，它的宽是4米，那么长是多少米？等量关系式：方程：2、一个长方形的周长为78.6厘米，长是27厘米 ,宽是多少厘米？等量关系式：方程：3、一个正方形的周长为27.8米，那么边长是多少米？等量关系式：方程：三、根据题目中关键句确定等量关系。

1、找出题目中的键句如：“比……多”、“比……少”、“是……的几倍”、“是……的几倍多几”、“是……的几倍少几”、“一共有”2、按照关键句中，文字表述的顺序列出等量关系式。

（1）“比……多”，这里的“多”就是“加”。

（注意：要用”比“后面的数量来加）例：男生人数比女生人数多6人等量关系式：女生人数+6人=男生人数（2）“比……少”，这里的“少”就是“减”。

（注意：要用”比“后面的数量来减）例：苹果比梨少12个等量关系式：梨的个数-12个=苹果个数（3）“是……的几倍”，要用“乘法”。

（注意：谁的几倍就谁乘倍数）例：长是宽的3倍等量关系式：宽X3=长（4）“是……的几倍多几”，“几倍多”是“先乘后加”。

数量关系和等量关系的区别
一、指代不同
1、等量关系：特指数量间的相等关系，是数量关系中的一种。

2、数量关系：是公务员考试中行测的一类题型。

主要考查考生快速理解和解决算数问题的能力。

二、特点不同
1、等量关系：数学题目中常含有多种等量关系，如果要求用方程解答时，就需找出题中的对等关系。

2、数量关系：数量关系的理解与计算能力的考查是通过数量关系这一题型来实现，对数量关系的理解和基本的数学运算能力，是人类智力的重要组成部分。

三、考察能力不同
1、等量关系：被减数=减数+差，差=被减数-减数，减数=被减数-差，加法等量关系式，加数=和-另一个加数，和=加数+加数。

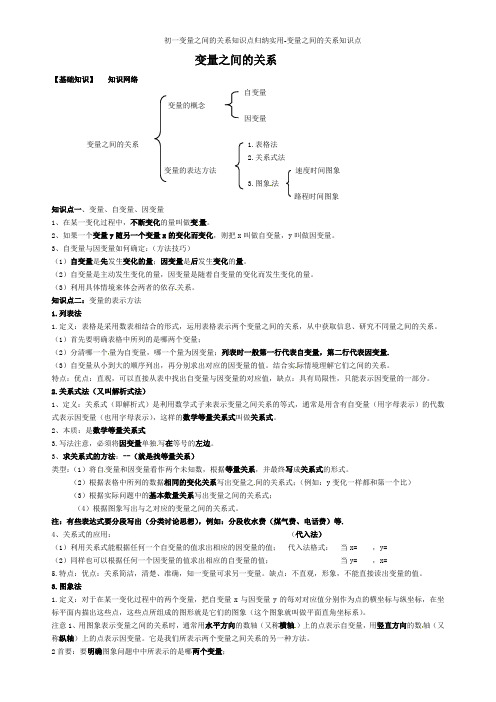
变量之间的关系【基础知识】知识网络自变量变量的概念因变量变量之间的关系 1.表格法2.关系式法变量的表达方法速度时间图象3.图象法路程时间图象知识点一、变量、自变量、因变量1、在某一变化过程中，不断变化的量叫做变量。

2、如果一个变量y随另一个变量x的变化而变化，则把x叫做自变量，y叫做因变量。

3、自变量与因变量如何确定：（方法技巧）（1）自变量是先发生变化的量；因变量是后发生变化的量。

（2）自变量是主动发生变化的量，因变量是随着自变量的变化而发生变化的量。

（3）利用具体情境来体会两者的依存关系。

知识点二：变量的表示方法1.列表法1.定义：表格是采用数表相结合的形式，运用表格表示两个变量之间的关系，从中获取信息、研究不同量之间的关系。

（1）首先要明确表格中所列的是哪两个变量；（2）分清哪一个量为自变量，哪一个量为因变量；列表时一般第一行代表自变量，第二行代表因变量.（3）自变量从小到大的顺序列出，再分别求出对应的因变量的值。

结合实际情境理解它们之间的关系。

特点：优点：直观，可以直接从表中找出自变量与因变量的对应值，缺点：具有局限性，只能表示因变量的一部分。

2.关系式法（又叫解析式法）1、定义：关系式（即解析式）是利用数学式子来表示变量之间关系的等式，通常是用含有自变量（用字母表示）的代数式表示因变量（也用字母表示），这样的数学等量关系式叫做关系式。

2、本质：是数学等量关系式3.写法注意，必须将因变量单独写在等号的左边。

3、求关系式的方法：--（就是找等量关系）类型：（1）将自变量和因变量看作两个未知数，根据等量关系，并最终写成关系式的形式。

（2）根据表格中所列的数据相同的变化关系写出变量之间的关系式；（例如：y变化一样都和第一个比）（3）根据实际问题中的基本数量关系写出变量之间的关系式；（4）根据图象写出与之对应的变量之间的关系式。

注：有些表达式要分段写出（分类讨论思想），例如：分段收水费（煤气费、电话费）等.4、关系式的应用：（代入法）（1）利用关系式能根据任何一个自变量的值求出相应的因变量的值；代入法格式：当x= ，y=（2）同样也可以根据任何一个因变量的值求出相应的自变量的值；当y= ，x=5.特点：优点：关系简洁，清楚、准确，知一变量可求另一变量。

这题怎么写,用方程解答列出等量关系式,正确采纳.方程是描述数学问题的一种工具，可以帮助我们用等量关系式解出问题的答案。

本文将为你展示如何用方程解答列出等量关系式，让你更顺利地解决类似的问题。

等量关系式等量关系式是一种表达等价关系的方法。

在数学上，等量关系式是指是两个量之间的等价关系，当两个量的值乘以一定的乘数后，它们的值仍为原值，也就是说，它们的值之比不变。

换句话说，两个量的值乘以一定的乘数后，结果与它们的原值是等价的。

通常，等量关系式会用数学方程的形式表达，这样就更容易理解和可操作。

等量关系式的特点1. 两个量的比值相等：等量关系式是指两个量之间的比值保持不变。

人们通常依据实际情况确定等量关系式，它们具有某种对称性、对应性或线性关系等特征，两个量之间的比值可以通过特定的一比较除以另一比较来表达。

2. 分号分隔：由于这种式子是用来表示两个量的相等性，所以它们的右边和左边之间要用分号“；”分隔开。

3. 通用性：等量关系式可以用来描述几乎任何可以变量赋值的量之间的关系。

例如，等量关系式可以用来表达时间、距离、体积、价格和其他量之间的变化关系。

用方程解答列出等量关系式这里有几种方式可以用方程解答列出等量关系式，具体如下：1. 基本形式：x=ax上式中，x和a是实数，有时也称为系数，表示它们之间比值的改变，||即|x/a|=a。

通常来说，当|x/a|保持不变（即a不变）时，x也不变，也就是说，两个量之间有等量关系。

2. 积形式：xy=axy该公式表达的是x和y之间的等量关系，xxx和yyy之间经常需要乘以一些系数（即a）才能得到它们之间的等量关系，当a不变时，x乘以y等于a乘以x乘以y，也就是说，它们之间有等量关系。

3. 分数形式：当两个量之间存在分数形式的等量关系时，可以用下式表示：a/b=c/d上面的式子中，a和b都是实数，也可以称为系数，它们表示另外两个实数c和d之间的比值变化，即a/b=c/d，而当这个关系中的系数a和b 不变时，c乘以d等于a乘以b，也就是说，其中也有等量关系。

等量关系式定义：等量关系式是表达数量间的相等关系的式子，如果要求用方程解答时，就需找出题中的等量关系，从而列出等量关系式。

常见关系式:减法等量关系式:被减数=减数+差差=被减数-减数减数=被减数-差加法等量关系式:加数=和-另一个加数和=加数+加数乘法等量关系式:积=因数×因数因数=积÷另一个因数除法等量关系式：被除数=除数×商商=被除数÷除数除数=被除数倍数等量关系式：每份数×份数=总数总数÷每份数=份数总数÷份数=每份数一、译式法将题目中的关键性语句翻译成等量关系。

(一)从关键语句中寻找等量关系。

1、关键句是“求和”句型的 .例:先锋水果店运来苹果和梨共720千克,其中苹果是270。

运来的梨有多少千克?2、关键句是“相差关系”句型。

关键词:比一个数多几,比一个数少几,例:小张买苹果用去7. 4元,比买橘子多用0. 6元,每千克橘子多少元?3、关键句是“倍数关系”句型。

饲养场共养2400只母鸡,母鸡只数是公鸡只数的2倍,公鸡养了多少只?4、有两个关键句,既有“倍数”关系,又有“求和”或者“相差”关系。

(必考考点) 一般把“和差”关系作为全题的等量关系式,倍数关系作为两个未知量之间的关系,用来设未知量。

(1倍数设为x ,几倍数设为几x 。

)如果只有和差关系的话,一般把求和关系作为全题的等量关系式,相差关系作为两个未知量之间的关系。

(把较小数设为x ,则较大数为x +a 。

)例:果园里共种240棵果树,其中桃树是梨树的2倍,这两种树各有多少棵?例:河里有鹅鸭若干只,其中鸭的只数是鹅的只数的4倍。

又知鸭比鹅多27只,鹅和鸭各多少只?例:后街粮店共运来大米986包,上午比下午多运14包,上午和下午各运多少包?二)没有关键句,找关键字上,寻找等量关系式。

“一共”、“还剩”例:网球场一共有1428个网球,每筒装5个,还剩3个。

装了多少筒? 例:一辆公共汽车上有乘客38人,在火车站有12人下车,又上来一些人,这时车上有乘客54人。

如何理解数学中的等量关系全文共四篇示例，供读者参考第一篇示例：数学中的等量关系是数学中非常重要的一个概念，它涉及到数学运算中的基本概念和规律。

理解数学中的等量关系不仅可以帮助我们更好地理解数学知识，还可以提高我们解题的能力和思维逻辑。

在数学学习中，掌握等量关系是非常重要的一环。

今天，我们就来详细了解一下数学中的等量关系。

什么是数学中的等量关系呢？等量关系指的是两个数或者两个式子的值相等的关系。

在数学中，我们会经常遇到这样的问题：给定两个式子或者表达式，我们需要通过运算来判断它们是不是等量关系。

对于简单的加法和减法运算，我们可以通过计算来确定它们的值是否相等。

在理解等量关系时，我们要注意以下几点：1. 等式的性质：在数学中，等式有自己的性质。

对于一个等式，我们可以在两边同时进行相同的操作，保持等式成立。

如果一个等式两边同时加上或者减去同一个数，等式仍然成立。

这是因为两边的值是相等的，所以它们经过相同的操作之后，仍然是相等的。

2. 等式的变形：在解题过程中，我们常常需要对等式进行变形。

变形是指通过一系列的等式变换，将原来的等式转化成另一个等式。

在变形的过程中，我们要注意保持等式的性质，确保等式的成立性不会受到改变。

3. 等式的解题方法：在解题时，我们可以通过代入法、等式变形法等方法来判断等式的成立性。

对于复杂的等式，我们需要通过逐步推导的方法来求解。

通过这些解题方法，我们可以更加直观地理解等量关系。

第二篇示例：在数学中，等量关系是指一个方程式表明两边的量是相等的关系。

在学习和理解数学中的等量关系时，我们需要重点关注方程中的变量和系数，以及如何通过代数运算来求解和验证等量关系。

本文将简要介绍如何理解数学中的等量关系，帮助读者更好地掌握这一概念。

一、理解等量关系的基本概念在数学中，等量关系通常以方程的形式呈现，例如：2x + 3 = 7。

这个方程表示左边的表达式2x + 3与右边的数7是相等的关系。

解这个方程，就是要找到使得等式成立的变量x的取值。

四年级等量关系公式(一)四年级等量关系公式一、等式的基本概念•等式的定义：等式是指相等关系成立的数学式，左右两边的值相等。

•等式的性质：等式具有传递性、对称性和可逆性。

二、等量关系的常见公式1.两数之和等于某数：a + b = c例如：3 + 4 = 7，表示3和4的和等于7。

2.两数之差等于某数：a - b = c例如：8 - 5 = 3，表示8减去5的差等于3。

3.两数之积等于某数：a * b = c例如：2 * 6 = 12，表示2和6的积等于12。

4.两数之商等于某数：a / b = c例如：10 / 2 = 5，表示10除以2的商等于5。

三、等量关系公式的应用举例1.填空题：根据已知的等量关系，填写缺失的数字。

示例题目：__ + 7 = 15，求出空缺的数字。

解答思路：根据等式的性质，可以通过反运算找出缺失的数字。

15减去7等于8，因此空缺的数字是8。

2.推理题：根据已知的等量关系，推导出其他可能的等式。

示例题目：如果a - b = 9，那么b - a = ?解答思路：根据等式的性质，两边同时改变符号不改变等式的成立。

因此，b - a的结果也应该是9。

3.实际问题：将实际问题转化为等量关系公式，以求解未知数。

示例问题：小明有一些饼干，他将其中的一半分给了小红，现在还剩下6块饼干。

求小明原先有多少块饼干。

解答思路：假设小明原先有x块饼干，根据问题的描述，可以列出等式：x / 2 = 6。

通过解方程可以求得x的值为12。

因此，小明原先有12块饼干。

以上就是四年级等量关系公式的相关内容，通过掌握这些公式和解题思路，可以帮助孩子更好地理解和应用等量关系。

等量关系式定义：等量关系式是表达数量间的相等关系的式子，如果要求用方程解答时，就需找出题中的等量关系，从而列出等量关系式。

常见关系式：减法等量关系式：被减数=减数+差差=被减数-减数减数二被减数-差加法等量关系式：加数二和-另一个加数和二加数+加数乘法等量关系式：积=因数/数因数=积吻一个因数除法等量关系式：被除数二除数^商商=被除数瑚数除数=被除数倍数等量关系式：每份数X份数=总数总数嗨份数=份数总数4份数= 每份数一、译式法将题目中的关键性语句翻译成等量关系。

（一）从关键语句中寻找等量关系。

1、关键句是求和”句型的.例:先锋水果店运来苹果和梨共720千克，其中苹果是270。

运来的梨有多少千克？2、关键句是相差关系”句型。

关键词:比一个数多几，比一个数少几，例:小张买苹果用去7. 4元,比买橘子多用0. 6元，每千克橘子多少元？3、关键句是倍数关系”句型。

饲养场共养2400只母鸡，母鸡只数是公鸡只数的2倍,公鸡养了多少只？4、有两个关键句，既有倍数”关系,又有求和”或者相差”关系。

（必考考点）一般把和差”关系作为全题的等量关系式，倍数关系作为两个未知量之间的关系，用来设未知量。

（1倍数设为x ,几倍数设为几x。

）如果只有和差关系的话，一般把求和关系作为全题的等量关系式，相差关系作为两个未知量之间的关系。

（把较小数设为x ,则较大数为x +a。

）例:果园里共种240棵果树,其中桃树是梨树的2倍,这两种树各有多少棵？例:河里有鹅鸭若干只，其中鸭的只数是鹅的只数的4倍。

又知鸭比鹅多27只,鹅和鸭各多少只？例:后街粮店共运来大米986包，上午比下午多运14包，上午和下午各运多少包？二）没有关键句，找关键字上，寻找等量关系式。

一共”还剩”例:网球场一共有1428个网球，每筒装5个,还剩3个。

装了多少筒？例:一辆公共汽车上有乘客38人，在火车站有12人下车，又上来一些人，这时车上有乘客54人。

在火车站上车的有多少人？（三）从常见的数量关系中找等量关系。

等量关系公式大全1.速度公式速度（v）=距离（s）/时间（t）速度（v）=v₀+a·t其中，v₀是初始速度，a是加速度，t是时间。

2.加速度公式加速度（a）=(v-v₀)/t其中，v是最终速度，v₀是初始速度，t是时间。

3.位移公式位移（s）=v₀·t+1/2·a·t²其中，s是位移，v₀是初始速度，a是加速度，t是时间。

4.力公式力（F）=质量（m）·加速度（a）力（F）=m·g其中，m是物体的质量，g是重力加速度。

5.动能公式动能（E）=1/2·m·v²其中，E是动能，m是物体的质量，v是物体的速度。

6.功公式功（W）= 力（F）·位移（s）·cos(θ)其中，W是功，F是施加的力，s是位移，θ是力和位移的夹角。

7.万有引力公式万有引力（F）=G·(m₁·m₂)/r²其中，F是万有引力，G是万有引力常数，m₁和m₂是两个物体的质量，r是两个物体之间的距离。

8.阻力公式阻力（Fₖ）=μ·N其中，Fₖ是阻力，μ是运动摩擦系数，N是物体所受的法向力。

9.法向加速度公式法向加速度（aₖ）=v²/R其中，aₖ是法向加速度，v是物体的速度，R是曲线的曲率半径。

10.电流公式电流（I）=电荷（Q）/时间（t）其中，I是电流，Q是电荷，t是时间。

11.电阻公式电阻（R）=电压（V）/电流（I）电阻（R）=ρ·(L/A)其中，R是电阻，V是电压，I是电流，ρ是电阻率，L是电阻器的长度，A是电阻器的横截面积。

12.串联电阻公式总电阻（Rₖ）=R₁+R₂+R₃+...其中，Rₖ是总电阻，R₁、R₂、R₃等是每个电阻的电阻值。

以上是一些常见的等量关系公式，通过这些公式可以描述和计算物质世界中的各种现象和问题。

不同学科和领域中还有更多的等量关系公式，需要根据具体情况进行学习和使用。

汇报人：文小库2023-11-29•方程等量关系的定义•方程等量关系的分类与识别•方程等量关系的建立与求解•方程等量关系的应用实例•方程等量关系的局限性及发展前景•总结与展望方程等量关系的定义01定义及公式方程等量关系是指两个或多个等式之间的一种关系，这种关系在等式的两边同时进行等量变换。

公式Ax+By=C方程等量关系具有双向性，即等式的两边同时进行等量变换。

双向性方程等量关系的等价性是指，在等式的两边进行等量变换后，等式仍然成立。

等价性方程等量关系的特点方程等量关系是解决各种实际问题的基本工具之一，例如在数学、物理、经济等领域中都有广泛的应用。

通过学习方程等量关系，可以培养人们的逻辑思维能力，提高对问题的分析和解决能力。

方程等量关系是数学学科中的基础概念之一，对于后续学习代数、几何等学科都有重要的意义。

解决问题培养逻辑思维能力基础学科方程等量关系的重要性方程等量关系的分类与识别02线性方程等量关系是指具有线性关系的两个或多个方程之间的等量关系。

一元一次方程、二元一次方程、多元一次方程等。

关注方程中的变量、系数和常数，判断是否符合线性关系的特点。

定义常见形式识别方法线性方程等量关系非线性方程等量关系是指不具有线性关系的两个或多个方程之间的等量关系。

一元二次方程、二元二次方程、高阶多项式方程等。

关注方程中的变量、系数和指数，判断是否符合非线性关系的特点。

定义常见形式识别方法非线性方程等量关系高阶方程等量关系是指含有高阶导数或高阶项的方程之间的等量关系。

定义高阶导数方程、高阶微分方程等。

常见形式关注方程中的高阶导数或高阶项，判断是否符合高阶方程的特点。

识别方法高阶方程等量关系微分方程等量关系是指含有导数或微分项的方程之间的等量关系。

定义常见形式识别方法常微分方程、偏微分方程等。

关注方程中的导数或微分项，判断是否符合微分方程的特点。

030201微分方程等量关系方程等量关系的建立与求解03建立等量关系根据题目描述，找出各个量之间的关系，建立等量关系。

等量关系式和方程式有什么区别
等量关系式是数学中的一种用语，与方程都表示相同意义。

它们不仅具有形式上的某些共性特征（如两个变量间可以建立起函数关系），而且二者之间还存在着许多内在联系：
方程在数学里指含有未知数；解方程时所得结果为已知数和待定系数的乘积或商的代数式叫做原方程或标准方程.只含有一个未知数
并且未知数的次数也是1的方程称为一元方程;对于2个及其以上未
知数的复合方程来说应当写成分别含有这几个未知数的方程的形式.。

- 1 -。

第五单元方程1.等量关系：等量关系是指数量之间具有的相等关系。

寻找等量关系的方法有很多，画图是最有效、最直观的方法。

2.方程的含义:含有未知数的等式叫方程。

方程可以表示等量关系。

3.方程与等式的联系区别:方程是等式，但等式却不都是方程。

4.解方程和方程的解：使方程左右两边相等的未知数的值叫作方程的解。

求方程的解的过程叫作解方程。

5.等式性质一:等式两边都加上（或减去）同一个数，等式仍然成立。

6.等式性质二:等式两边都乘一个数（或除以一个不为0的数），等式仍然成立。

7.解方程的书写格式:解方程前要先写一个“解”字和冒号;一步一脱式，每算一步，等号都要上、下对齐﹔表示未知数的字母一般都要放在等号的左侧。

8.看图列方程：关键是看懂图意，从中找出等量关系，然后再根据等量关系列出方程。

在列方程时，把未知数尽量放在等式左边。

9.用方程解决实际问题（解应用题）：首先要用字母表示未知数，然后根据题目中数量之间的相等关系，列出一个含有未知数的等式（也就是方程）再解出来，最后检验，写出答语。

从关键语句中寻找等量系1.关键句是“求和关系”句型。

例:先锋水果店运来苹果和梨共720千克，其中苹果是270千克。

运来的梨有多少千克?理解:720千克由两部分组成:一部分是苹果，一部分是梨子。

苹果 + 梨 =720 ⟹270 + x =720用等式表示出下面的数量关系:1.学校共购进单人书桌和双人书桌120套，其中单人书桌59套，那么购进双人书桌多少套？2.在某一次捐款活动中，四年级一班共捐款740元，其中男生捐款360元，女生捐款多少元？2.关键句是“相差关系”句型。

关键词:比一个数多几，比一个数少几。

例:小张买苹果用去7.4元，比买2千克橘子多用0，6元，每千克橘子多少元?理解:苹果与橘子相比较，多用了0.6元。

(推荐)直译法列式:从“比”字后面开始列橘子+0.6=苹果⟹ 2x + 0.6 =7.4比较法列式:较大数一较小数=相差数苹果一橘子=0.6元⟹ 7.4 -2x =0.6用等式表示出下面的数量关系:1.农场有37头水牛，黄牛比水牛多18头，黄牛有多少头？2.学校买了56张白纸，买的红纸比白纸多18张.红纸买了多少张?3.停车场上的小轿车比面包车多15辆，面包车有12辆，小轿车有多少辆？4.(1)学校有40个足球，篮球比足球多7个，篮球有多少个?（2）学校有40个足球，33个篮球，足球比篮球多多少个?5.(1)孙桥小学去年买桌椅50套，今年又买了58套，今年比去年多买了多少套?（2）孙桥小学去年买桌椅50套，今年比去年多买了8套，今年买了多少套?6.同学们去登山，男同学去了28人，女同学去了23人，女同学比男同学少去多少人?一共去了多少人？7.二一班参加书法组的有19人，参加文艺组的比书法组的少4人，参加文艺组的有多少人?8.水果商店运来两种水果，其中苹果有56筐，比运来的桃子筐数多13筐，水果店一共运来水果多少筐?3.关键句是“倍数关系”句型。

====Word行业资料分享--可编辑版本--双击可删====应用题常用等量关系式一、行程问题：速度×时间=路程（一）相遇问题：1、同时出发（两段）：甲的路程+乙的路程=总路程2、不同时出发（三段）：先走的路程+甲的路程+乙的路程=总路程（二）追及问题：（快者的速度－慢者的速度）×追及所用的时间=两者相距的路程1、不同地点出发：慢者行驶的路程+两者相距的路程=快者行驶的路程2、同地不同时出发：慢着先走的路程+慢者后走的路程=快者走的路程（三）飞行、航行的速度问题：顺水速度=静水速度+水流速度逆水速度=静水速度－水流速度二、利润、利率问题：（一）利润问题：售价=标价×打折数利润=售价－进价利润率=（利润÷进价）×100℅=（售价－进价）÷进价×100﹪进价=利润÷利润率利润=进价×利润率售价－进价=进价×利润率=利润销售额=售价×销售量（二）利率问题：利息=本金×利率×存期（年数、月数）本息和=本金+利息=本金+本金×利率×存期三、工程问题（一般把工作总量设为单位1）工作总量=工作效率×工作时间各工作量之和=总工作量各队合作工作效率=各队工作效率之和四、等积、等长问题长方形的周长=（长+宽）×2 长方形面积=长×宽正方形的周长=边长×4 正方形的面积=边长×边长圆的周长=πd=2πr 圆的面积=π r²长方体体积=长×宽×高圆柱体体积=底面积×高五、分段计费问题：应交缴费用=标准内费用+超标部分费用源-于-网-络-收-集。