下载文档原格式
7.1第7讲 一致收敛的概念与判别法所谓函数项级数是指级数的每项均为某一变量或多个变量的函数的级数，也就是说是无穷多个函数求和的问题，研究函数项级数主要回答下列几个问题：1. 收敛区域，即对于函数项级数：()1n n a x ∞=∑，x 在什么范围内级数是收敛的？这一问题是平凡的，因为对于给定x ，由数项级数之收敛性即可判别级数的收敛性，从而确定x 之收敛域。
2. 设()()1n n S x a x ∞==∑是收敛的，若()n a x 均为连续函数，问()S x 是否连续？回答是不一定。
例如：当1x <时，()1n n a x x −=，则有()11S x x=−，()n a x 在1x =处左连续，但()S x 在1x =处不是左连续的。
问题还可以提为：什么时候()S x 连续？ 3. 可导性能否保持？即：若()n a x 均为可导函数，问()S x 是否可导？同样有问题：什么时候可导性可以保持？特别地，如果均可导，()S x 的导数与()n a x 的导数有何关系？4. 可积性问题。
即：若()n a x 均为可积函数，问()S x 是否可积？何时可积？它们的积分有何关系？ 为了研究上述几个问题，我们需要引进“一致收敛”的概念。
7.2§1 一致收敛的概念讨论级数的收敛性实质上是其部分和函数()n S x 的性质，因此我们先考虑极限过程()()lim n n S x S x →∞=的性质。
上面所说的关于和函数的连续性，可导性、可积性有一个共同的特点，就是某一点x 处的连续性与可导性均与函数在该点邻域的性质有关，而不仅仅只与该点函数值相关，而可积性则更是函数在某一区间内的性质了。
另一方面，函数序列()n f x 在0x x =处是否收敛实际上只是数列()0n f x 的性质，与0x 点邻域内的性质是不相干的，因此从这一角度看，我们知道收敛性是无法用来描述其极限函数之性质的，因而有必要引入新的概念来区分不同的收敛性，以刻画函数序列的极限函数的性质。
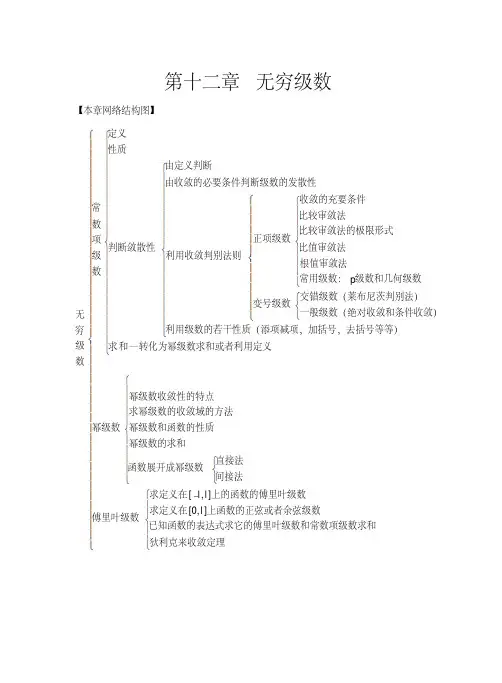
第十二章 无穷级数一、基本要求及重点、难点1．基本要求(1)理解无穷级数收敛、发散以及和的概念，了解无穷级数的基本性质及收敛的必要条件。
(2)了解正项级数的比较审敛法以及几何级数与P —级数的收敛性，掌握正项级数的比值审敛法。
(3)了解交错级数的莱布尼茨定理，会估计交错级数的截断误差。
了解绝对收敛与条件收敛的概念及二者的关系。
(4)了解函数项级数的收敛域与和函数的概念，掌握简单幂级数收敛区间的求法（区间端点的收敛性不作要求）。
了解幂级数在其收敛区间内的一些基本性质（对幂级数的和函数只要求作简单训练）。
(5)会利用)1ln(,cos ,sin ,x x x e x+与α)1(x +的马克劳林（Maclaurin ）展开式将一些简单的函数展开成幂级数。
(6)了解利用将函数展开为幂级数进行近似计算的思想。
(7)了解用三角函数逼近周期函数的思想，了解函数展开成傅立叶（Fourier ）级数的狄利克雷（Dirichlet ）条件，会将定义在),(ππ-和),(l l -上的函数展开成傅立叶级数，会将定义在),0(l 上的函数展开为傅立叶正弦级数或余弦级数。
2．重点及难点（1） 重点：掌握正项级数的审敛法，能对幂级数审敛及会把某些函数展开成幂级数。
（2） 难点：一般项级数的审敛法，求幂级数的和函数，将函数展开成幂级数。
二、内容概述1．常数项级数（1）一般概念定义 给定一个数列{}n u ，对它的各项依次用“+”号连接起来的表达式++++n u u u 21，称为级数，记为∑∞=1n n u ，其中第n 项n u 叫做级数的一般项；级数的前n 项和∑==+++=nk kn n uu u u s 121 称为级数的第n 个部分和，简称部分和。
定义 如果级数∑∞=1n nu的部分和数列{}n s 有极限s ，即若s s n n =∞→lim ，则称无穷级数∑∞=1n nu收敛，这时极限s 叫做该级数的和，并写成 =s ∑∞=1n nu; 如果{}n s 没有极限，则称级数∑∞=1n nu发散。
