当前位置：文档之家 › §4用向量讨论垂直与平行

§4用向量讨论垂直与平行

  • 格式：ppt
  • 大小：499.50 KB
  • 文档页数：58

下载文档原格式

  / 58

合集下载

§4 用向量讨论垂直与平行

§4 用向量讨论垂直与平行

nav则,,
v b
与
平面α共面,一条直线l的
l
// 或l在内
存在两个实数x,
y, 使n
xa
yb
3.面面平行
两个不共线的向量
a,
v b 与平面α共面,则
// 或与重合 a//
且b//
mn
av v b
nv
l
av
v b
例3.（面面平行判定定理）若一个平面内有两条相交直线都平
行于另一个平面, 则这两个平面平行.
a // , b //
nv2
av
//
,
v b
//
nv2
nv2
av,
nv2
v b
aI b P
nnvv12
nv1 // nv2 //
练习3.如图所示,
已知斜三棱柱ABC-A1B1C1,
设
uuuv AB
av,
uuuv AC
v b,
uAuAuuuAuMuv1uvcvk, 在uAuCu面uv1,对uBu角Nuv线 AkCuBu1Cu上v(0和棱kBC1上). 分别取点AM1 、N, 使
D1B1的中点.求证EF⊥平面B1AC.
z
证法2: 如图建立空间直角坐标系D-xyz,
D1
F
C1
u设uBuv正1(2方,2体,2)的, E棱(2长,u2u,为u1v),2F，则(1,A1(,22),0 ,u0u)uv, C(0,2,0）A1
B1
EF (1, 1,1), AC (2, 2, 0), AB1 (0, 2, 2)
B
EF // B1D1
在正方体ABCD-A1B1C1D1中，
AC EF

4.用向量讨论垂直和平行问题

4.用向量讨论垂直和平行问题

练习：如果一个平面经过另一个平面的一条垂线， 那么这两个平面互相垂直.
（一）用向量处理平行问题
例1: 如图已知四边形ABCD、 ABEF为两个正方形, MN 分别在其对角线BF 上,
F M E
B
C
N 且FM AN .求证：MN // 平面EBC A 证明 : 在正方形ABCD与ABEF中, D BE AB, FM AN , , FB AC 存在实数, 使FM FB, AN AC. MN MF FA AN BF EB AC ( BE BA AB AD) EB ( BE AD) EB ( BE BC ) BE ( 1) BE BC.
作业：1. 如图, 直三棱柱ABC A1 B1C1中, ACB 90 ,
0
AC 1, CB 2, 侧棱AA1 1, 侧面AA1B1B的 两条对角线交点为D, B1C1的中点为M . 求证CD 平面BDM
A Z
A1
D
B X
A1B, DM 为平面BDM内的两条相交直线, CD 平面BDM .
两条对角线交点为D, B1C1的中点为M . 求证CD 平面BDM
A
A1
解:
如图,以C为原点建立空间直角坐标系. B( 2 ,0,0), B1 ( 2,1,0), A1 (0,1,1),
D
C
C1
M Y
B1
2 1 1 2 B D( , , ), M ( ,1,0), 2 2 2 2 X 2 1 1 1 1 CD ( , , ), A1 B ( 2, 1, 1)， (0, , ), DM 2 2 2 2 2

用向量讨论垂直于平行

用向量讨论垂直于平行

用向量讨论垂直于平行部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑设计人：雷义平教师寄语：不要等待机会，而要创造机会。

时间---------------- 班级---------- 学生姓名-------- -----------§2-4《用向量讨论平行与垂直》问题导读---评价单学习目标：1．理解用向量方法解决立体几何问题的思想。

2．掌握用向量方法证明立体几何中的线、面的垂直与平行问题。

学习重难点：1、空间直角坐标系的正确建立，空间向量的运算及其坐标表示2、用向量语言证明立体几何中有关垂直、平行关系的问题.学习过程：一、阅读文本，解决以下问题。

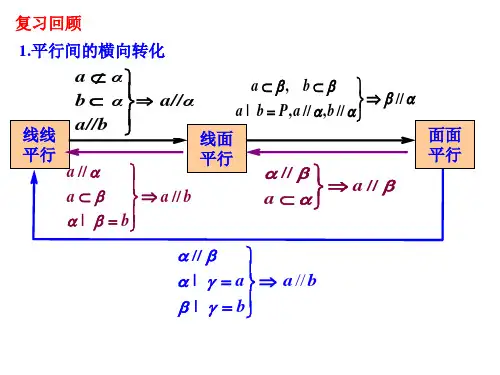
1.怎样确定直线的方向向量？2.怎样确定平面的法向量？3.如何利用向量知识判断直线与平面间的平行或垂直问题？4.用向量语言表述线与面之间的平行与垂直关系. 设空间直线、的方向向量分别为、，平面的法向量分别为、，则：b5E2RGbCAP①线线平行：或与重合即：两直线平行或重合两直线的方向向量共线。

②线线垂直：即：两直线垂直两直线的方向向量垂直。

③线面平行：且在平面外即：直线与平面平行直线的方向向量与该平面的法向量垂直且直线在平面外。

④面面平行：或与重合即：两平面平行或重合两平面的法向量共线。

⑤线面垂直：即：直线与平面垂直直线的方向向量与平面的法向量共线直线的方向向量与平面内两条不共线直线的方向向量都垂直。

⑥面面垂直： 5. 求平面法向量的方法步骤：p1EanqFDPw6. 三垂线定理：二．我的疑惑：问题解决---评价单1、平面α的一个法向量为(1,2,0>，平面β的一个法向量为(2，－1,0>，则平面α与平面β的关系是( >DXDiTa9E3dA．平行 B．相交但不垂直C．相交且垂直 D．无法判定2、在空间四边形ABCD中，E，F分别是AB，BC的中点，则AC与平面DEF的位置关系是( >A．平行 B．相交C．在平面内 D．不能确定3、已知一平面的法向量为(1,2，－1>，则与此平面垂直的向量可以是( >A．(2,4，－2> B．(1，－1，－1>C．(0,1,2> D．(1,0，－1>4、在正方体AC1中，O1为B1D1的中点，求证：BO1∥平面ACD1.问题拓展---评价单1 如下图所示，在平行六面体ABCD－A1B1C1D1中，E，F，G分别是A1D1，D1D，D1C1的中点．求证：平面EFG∥平面AB1C.RTCrpUDGiT2 ABC－A1B1C1是各条棱长均为a的正三棱柱，D 是侧棱CC1的中点．求证：平面AB1D⊥平面ABB1A1.申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

《用向量讨论垂直与平行》第一课时参考教案

《用向量讨论垂直与平行》第一课时参考教案

2.4 用向量讨论垂直与平行 第一课时教案一、教学目标：1．理解直线的方向向量和平面的法向量； 2．会用待定系数法求平面的法向量。

二、教学重点：直线的方向向量和平面的法向量；教学难点：求平面的法向量 三、教学方法：探究归纳，讲练结合 四、教学过程 （一）、创设情景1、平面坐标系中直线的倾斜角及斜率，直线的方向向量，直线平行与垂直的判定；2、如何用向量描述空间的两条直线、直线和平面、平面和平面的位置关系？ （二）、探析新课 1、直线的方向向量我们把直线l 上的向量e 以及与e 共线的向量叫做直线l 的方向向量 2、平面的法向量如果表示向量n 的有向线段所在直线垂直于平面α，则称这个向量垂直于平面α，记作α⊥，如果α⊥，那么向量叫做平面α的法向量。

（三）、知识运用1、例1 在正方体1111D C B A ABCD -中，求证：1DB 是平面1ACD 的法向量证：设正方体棱长为1，以1,,DD 为单位正交基底， 建立如图所示空间坐标系xyz D -)1,1,1(1=DB ，)0,1,1(-=AC ，)1,0,1(1-=AD 01=⋅DB ，所以DB ⊥1同理11AD DB ⊥ 所以⊥1DB 平面ACD从而1DB 是平面1ACD 的法向量。

2、 例2 在空间直角坐标系内，设平面α经过点),,(000z y x P ，平面α的法向量为),,(C B A =，),,(z y x M 为平面α内任意一点，求z y x ,,满足的关系式。

解：由题意可得),,(000z z y y x x PM ---= 0=⋅即0),,(),,(000=---⋅z z y y x x C B A 化简得0)()()(000=-+-+-z z C y y B x x A 3、课堂练习已知点P 是平行四边形ABCD 所在平面外一点，如果(2,1,4)AB =-，(4,2,0)AD =，(1,2,1)AP =--（1）求证：AP 是平面ABCD 的法向量； （2）求平行四边形ABCD 的面积．（1）证明：∵(1,2,1)(2,1,4)0AP AB ⋅=--⋅--=，(1,2,1)(4,2,0)0AP AD ⋅=--⋅=，∴AP AB ⊥，AP AD ⊥，又AB AD A =，AP ⊥平面ABCD ，∴AP 是平面ABCD 的法向量．（2）||(2)AB ==2||4AD ==， ∴(2,1,4)(4,2,0)6AB AD ⋅=--⋅=，∴cos(,)105AB AD ==，∴sin BAD ∠==∴||||sin ABCDSAB AD BAD =⋅∠=（四）、回顾总结：1、直线得方向向量与平面法向量得概念；2、求平面法向量的方法。

2-3-4用向量讨论垂直与平行课件(北师大版选修2-1)

2-3-4用向量讨论垂直与平行课件(北师大版选修2-1)

课前探究学习
课堂讲练互动
活页限时训练
→ n· ＝0， （x，y，z）· DM （0，2，1）＝0， 则 即 → （1，2，0）＝0， n· ＝0， （x，y，z）· DN 令 y＝1 得 x＝－2，z＝－2，∴n＝(－2，1，2)， → → ∴A1P＝n，∴A1P∥n， ∴A1P⊥平面 DMN.
的棱 CC1、BC、CD 的中点，求证：A1P⊥平面 DMN.
课前探究学习
课堂讲练互动
活页限时训练
证明
法一 如图，建立空间直角坐标系，设正方体棱长为 2，
则有 D(0，0，0)，A1(2，0，2)，P(0，1，0)，M(0，2，1)，N(1， 2，0)． → → → ∴A1P＝(－2，1，－2)，DM＝(0，2，1)，DN＝(1，2，0)， → → → → ∴A1P·DM＝0，A1P·DN＝0. ∴A1P⊥DM，A1P⊥DN， 又 DM∩DN＝D， ∴A1P⊥平面 DMN.
课堂讲练互动
活页限时训练
1 1 → n· ＝0， －2x0－2y0－z0＝0， OD 则 得 n·→ ＝0， －1x ＋1y ＝0. OC1 2 0 2 0 令 x0＝1，得 y0＝1，z0＝－1，∴n＝(1，1，－1)． → 又B1C·n＝－1×1＋0×1＋(－1)×(－1)＝0， → ∴B1C⊥n，∴B1C∥平面 ODC1.
课前探究学习
课堂讲练互动
活页限时训练
本题将证明线线平行问题转化为空间向量共线问 题，尤其是引进空间坐标系后使得解题思路更加清晰明了．
课前探究学习
课堂讲练互动
活页限时训练
【训练 2】 在正方体 ABCD- 1B1C1D1 中，O 是 B1D1 的中点， A 求证：B1C∥平面 ODC1. 证明 → → 法一 ∵B1C＝A1D，B1∉A1D，∴B1C∥A1D，

用向量方法解决平行与垂直问题 课件

用向量方法解决平行与垂直问题 课件

，B
0，a，0 2
，
C 23a，0，0 ，D 0，a2，a2 ，E 23a，0，a ， 2分
∴A→D＝0，a，a2，A→C＝ 23a，a2，0， A→E＝ 23a，a2，a. 设面 ADE 的一个法向量为 n1＝(x，y，z)，
由 nn··AA→→DE＝＝00
ay＋a2z＝0，
⇔
23ax＋a2y＋az＝0.
● (1)线线垂直：①可以证明两直线的方向向量的数量积为0.
● ②可以证明两直线所成角为直角．
● (2)线面垂直：①根据判定定理转化为线线垂直．
● ②证明直线的方向向量与平面的法向量平行．
● (3)面面垂直：①根据判定定理证明线面垂直．
● ②证明两个平面的法向量垂直．
判定或证明垂直关系的方法主要是用判定定理或直线的方向向量、平面的法向量间的关系进行的．
求空间平面的法向量
●
正方体ABCD－A1B1C1D1的棱长为2，E，F分别为棱
A1D1，A1B1的中点，求平面EFBD的一个法向量．
思路点拨： 建立空间直角坐标系 → 相关点坐标 →
→→ DB，DE坐标
→
设法向量n＝x，y，z，由nn··DD→→BE＝＝00
用向量方法解决平行与垂直问题
直线的方向向量与平面的法向量
● 1．直线的方向向量的定义
● 直线的方向向量是指和这条直线____共__线__或__平__行的向量．
● 2．平面的法向量的定义
● 直线l⊥α，取直线l的_____方__向__向__量_，a 则a叫做平面α的法向量．
对直线的方向向量和平面的法向量的几点认识 (1)空间中任意一条直线 l 的位置可以由 l 上一个定点 A 以及一个方向确定．在直线 l 上取A→B＝a，a 可以作为 l 的方 向向量，借助点 A 和 a 即可确定直线 l 的位置，并能具体表 示出直线 l 上的任意一点．

高中数学-4-用向量讨论垂直与平行

高中数学-4-用向量讨论垂直与平行

(1)证明：设 E(0，a，z)， 则A→1E＝(－a，a，z－a)，B→D＝(－a，－a,0)， ∴A→1E·B→D＝a2－a2＋(z－a)×0＝0，
∴A→1E⊥B→D，即 A1E⊥BD．
(2)E 为 CC1 的中点．证明如下： 由 E 为 CC1 的中点得 E(0，a，a2)， 设 BD 的中点为 O，则 O(a2，a2，0)， O→E＝(－a2，a2，a2)，O→A1＝(a2，－a2，a)， B→D＝(－a，－a,0)，则O→E·B→D＝0，O→A1·B→D＝0.∴O→E⊥B→D，O→A1⊥B→D， ∴∠A1OE 为二面角 A1－BD－E 的平面角， 由O→A1·O→E＝0，则∠A1OE＝90°，∴平面 A1BD⊥平面 EBD．
＝(-a,a,-a)，∴n2＝1aB→1D＝(-1,1,-1)为面 A1BC1
的一个法向量．
(2)M 为 CD 中点，求面 AMD1 的一个法向量． 解：设 n＝(x0，y0，z0)为面 AMD1 的法向量， ∵A→M＝(a2，a,0)，A→D1＝(0，a，a)， ∴n·A→M＝x0，y0，z0·a2，a，0＝a2x0＋ay0＝0，
n·A→D1＝x0，y0，z0·0，a，a＝ay0＋az0＝0. 令 x0＝2，则 y0＝－1，z0＝1， ∴n＝(2，－1,1)为面 AMD1 的一个法向量．
求一个平面的法向量，主要有以下两种方法： 1．找该平面的垂线，以该垂线的方向向量为该平面的法向量． 2．对于一般位置状态的平面，采用以下步骤求法向量．
图 2－4－2 【思路探究】 要证明两个平面垂直，由两个平面垂直 的条件，可证明这两个平面的法向量垂直，转化为求两个平 面的法向量 n1，n2，证明 n1·n2＝0.
【自主解答】由题意得 AB,BC,B1B 两两垂直, AB＝BC＝2，BB1＝1， E 为 BB1 的中点．以 B 为原点，BA，BC，BB1 分别为 x，y，z 轴，

§4用向量讨论垂直与平行 (1)

§4用向量讨论垂直与平行 (1)
7
用空间向量证明立体几何中的垂直
1.证明线面垂直：
（1）求出这条直线 的方向向量和平面 的法向量，证明这 两个向量平行（2） 在平面内任找两个 不共线的向量与这 条直线的方向向量 垂直。
2.证明面面垂直：
（1）分别求出这两 个平面的法向量， 证明这两个向量垂 直； （2）先用向量证明 线面垂直，再证明 面面垂直。
8
作业
1.学案1、2、3、4、5； 2、用向量语言表述平行 与垂直的八个定理。
9
（1）线面垂直判定定理 （2）面面平行判定定理 （3）三垂线定理
4
三、拓展运用
Z
E
F X
Y
5
四、学习总结6源自 用空间向量证明立体几何中的平行1.证明线面平行： 求出这条直线的 方向向量和平面 的法向量，证明 这两个向量垂直。 2.证明面面平行： （1）分别求出这两 个平面的法向量 ，证明这两个向 量平行； （2）先用向量证明 线面平行，再证 明面面平行。
学习目标
1.能用向量语言表述线线、线面、面面的垂直 、平行关系。 2.能用向量方法证明有关线、面位置关系的一 些定理。 3.体会学习的快乐。
2.4用向量讨论垂直与平行
雪枫中学 李静
一、温故探新
1.什么是直线的方向向量？
2什么是平面的法向量？ 回顾向量知识，完成学案
3
二、合作学习
用空间向量证明

§4用向量计议垂直于平行

§4用向量计议垂直于平行

l2 的位置关系（ ）
A 平行 B 相交 C 垂直 D 不能确定

2、若两平面1 、2 的法向量分别为 n1 1, 0, 2、 n2 1, 0, 2，则两条直线 l1 、
1
对全部高中资料试卷电气设备，在安装过程中以及安装结束后进行高中资料试卷调整试验；通电检查所有设备高中资料电试力卷保相护互装作置用调与试相技互术关，通系电1，力过根保管据护线生高0不产中仅工资2艺料22高试2可中卷以资配解料置决试技吊卷术顶要是层求指配，机置对组不电在规气进范设行高备继中进电资行保料空护试载高卷与中问带资题负料2荷试2，下卷而高总且中体可资配保料置障试时2卷，32调需3各控要类试在管验最路；大习对限题设度到备内位进来。行确在调保管整机路使组敷其高设在中过正资程常料1工试中况卷，下安要与全加过，强度并看工且25作尽52下可22都能护可地1关以缩于正小管常故路工障高作高中；中资对资料于料试继试卷电卷连保破接护坏管进范口行围处整，理核或高对者中定对资值某料，些试审异卷核常弯与高扁校中度对资固图料定纸试盒，卷位编工置写况.复进保杂行护设自层备动防与处腐装理跨置，接高尤地中其线资要弯料避曲试免半卷错径调误标试高方中等案资，，料要编试求5写、卷技重电保术要气护交设设装底备备置。4高调、动管中试电作线资高气，敷料中课并设3试资件且、技卷料中拒管术试试调绝路中验卷试动敷包方技作设含案术，技线以来术槽及避、系免管统不架启必等动要多方高项案中方；资式对料，整试为套卷解启突决动然高过停中程机语中。文高因电中此气资，课料电件试力中卷高管电中壁气资薄设料、备试接进卷口行保不调护严试装等工置问作调题并试，且技合进术理行，利过要用关求管运电线行力敷高保设中护技资装术料置。试做线卷到缆技准敷术确设指灵原导活则。。：对对在于于分调差线试动盒过保处程护，中装当高置不中高同资中电料资压试料回卷试路技卷交术调叉问试时题技，，术应作是采为指用调发金试电属人机隔员一板，变进需压行要器隔在组开事在处前发理掌生；握内同图部一纸故线资障槽料时内、，设需强备要电制进回造行路厂外须家部同出电时具源切高高断中中习资资题料料电试试源卷卷，试切线验除缆报从敷告而设与采完相用毕关高，技中要术资进资料行料试检，卷查并主和且要检了保测解护处现装理场置。设。备高中资料试卷布置情况与有关高中资料试卷电气系统接线等情况，然后根据规范与规程规定，制定设备调试高中资料试卷方案。

用向量讨论垂直和平行(课堂PPT)

用向量讨论垂直和平行(课堂PPT)

与平行获得处理这类问题的方法。
3 认识事物之间的规律性，进一步体会向量方法 在立体几何中的具体作用。
5
导学案反馈
闪光点：1、按时交导学案； 2、对课本认真解读了，对知识达到了一定的理
解； 态度方面：个别卷面不整洁； 知识理解方面：
1、求点的轨迹是要注意建系设点（合作探究2） 2、当不确定椭圆的焦点在哪个坐标轴上时，要注 意讨论。（合作探究3）
另一个平面，则这两个平面平行。
14
例 2.在 正 方 形 A B C D-A 1B 1C 1D 1 中 ,
求 证 :平 面 A 1B D//平 面 C B 1D 1
证明:如图分别以D1A1、D1C1、D1D
三边所在的直线为x,y,z轴建立空间 A
直角坐标系.设正方体的棱长为1,
Z
D
C
B
则A1(1,0,0),B1(1,1,0),
求证CD 平面BDM
A
A1
解 :
D
如 图 ,以 C为 原 点 建 立 空 间 直 角 坐 标 系 .
B( 2,0,0),B1( 2,1,0),A1(0,1,1),
C
C1
MY
B1
D( 2,1,1),M( 2,1,0),
B
2 22 2
X
uuur CD(
2, 2
1, 2
12),uAu1uBr (
uuuur 2,1,1)，DM(0,
C'
A'
底面是正三角形，AA' 底面ABC，
A'C AB',求证：BC' AB'
证明：设底面边长 1, 为
设a AA',b AB,c AC C

空间向量与立体几何 第四节 用向量讨论垂直与平行(精讲精练)

空间向量与立体几何 第四节 用向量讨论垂直与平行(精讲精练)

z
O1 A1 B1 C1
O A
C E B F
y
x
即
2 y 2z 0 2 例 1. 证：如图，建立空间直角坐标系 A－xyz，设 AB＝2a，BC＝2b，PA＝2c，则：A(0, 0, 0)，B(2a, 0, 0)，C(2a, 2b, 0)，D(0, 2b, 0)，P(0, 0, 2c) ∵ E 为 AB 的中点，F 为 PC 的中点∴ E (a, 0, 0)， 2 x 2 y 2z 0 → → → →1 →→ → → F (a, b, c)(1)∵ EF ＝(0, b, c)， AP ＝(0, 0, 2c)， AD ＝(0, 2b, 0)∴ EF ＝ ( AP ＋ AD ) ∴ EF 与 AP 、 2 2 2
10. 如图，在四棱锥 O
ABCD中ቤተ መጻሕፍቲ ባይዱ底面 O
ABC
ABCD 四边长
为 1 的 菱 形 ，

4
,
M
（A） 5
（B）
5 3 （C）
10
（D）
10 3
OA 底面ABCD , OA 2 , M
OA 的中点， N
为 BC 的中点 ；
为
A B N C
D
2．已知 a、b、c 是空间三非零向量，若︱a－b－c︱＝︱a ︱＋︱b︱＋︱c︱,则在下列各结论中，正确的结论为（ （A）a、b、c 同向 （B）a 与 b 同向 （D）a 与－(b+c)反向 ）
5 设 M、 N 是直角梯形 ABCD 两腰的中点， DE⊥AB 于 E(如图)． 现 将△ADE 沿 DE 折起，使二面角 A－ DE－B 为 45° ， 此时点 A 在平面 BCDE 内的射影恰为点 B，则 M、N 的连线与

用向量讨论垂直与平行

用向量讨论垂直与平行

第四节 用向量讨论垂直与平行一、教学目标1、知识与技能：掌握用向量方法证明立体几何中的线、面的垂直与平行问题。

2、过程与方法：通过对定理的证明，认识到向量是解决立体几何问题的基本方法。

3、情感、态度与价值观：用向量的方法证明立体几何中的定理，培养学生从多角度研究立体几何问题的能力。

二、教材分析本节所涉及到的定理，学生都已经学习过，这里主要是要让学生体会用向量方法解决几何问题的过程。

本节没有给出必修中线面关系的所有定理，只选取部分，目的是留给学生自学的机会。

例1（线面平行判定定理）使学生认识到直线的方向向量决定直线的方向，并为建立空间直角坐标系打下基础。

例2（面面平行判定定理）使学生认识到平面法向量决定平面位置的确定。

虽然平面的法向量有无数个，但是他们都是共线的。

三、重点和难点重点：用向量的方法证明立体几何的垂直与平行问题； 难点：用向量语言证明立体几何中的垂直与平行问题。

四、教具准备：直尺、粉笔、黑板 五、课时安排：1课时 六、教学过程《一》直接引入向量是研究立体几何的基本工具，从本节开始，我们将用向量研究立体几何的一些问题。

《二》推进新课例1、证明线面垂直判定定理（转化为证明直线的方向向量垂直） 已知：如图，c b ,是平面π内的两条相交直线，直线a 满足b a ⊥，c a ⊥ 求证：π⊥a证明：设直线p 是平面π设直线a,b,c,p 的方向向量分别是p c b a,,,只需证p a⊥c a b a c a b a ⊥⊥∴⊥⊥,, 0,0=∙=∙∴c a b a直线b ，c 相交 ∴b 与c不共线又 因为直线b ，c ，p 在同一平面π内∴存在实数μλ,，使得： c b pμλ+=∴ 0=∙p a ，即p a ⊥∴直线a 垂直于平面π)()(c a b a p a ∙+∙=∙∴μλ例2已知：如图，a 与b 是平面1π内两条相交直线 平面2π满足2||πa ，2||πb 求证：21||ππ证明：设直线a ，b 的方向向量分别为b a,平面21,ππ的法向量分别为21,n n ，只要证21||n n22||,||ππb a 22||,||ππb a∴ b n a n ⊥⊥∴22,又 a 与b 是平面1π内的相交直线 ∴2n也是1π的方向量 ∴21||n n∴21||ππ《三》思考交流 求证：（面面垂直判定定理）若一个平面经过另一个平面的垂线，则这两个平面垂直。

4[1].用向量讨论垂直和平行

4[1].用向量讨论垂直和平行

B
小结
三、小结
利用向量解决平行与垂直问题 向量法：利用向量的概念技巧运算解决问 题。 坐标法：利用数及其运算解决问题。 两种方法经常结合起来使用。
作业：课本p.41第1,2,3题。
Bye－bye!
复习回顾
1.线面垂直的判定定理： 若一条直线垂直于一个平面内的两条相交 直线，则该直线与该平面垂直。
2.面面垂直的判定定理： 如果一个平面经过另外一个平面的一条垂线， 则这两个平面垂直。
3.线面平行的判定定理： 如果平面外一条直线平行于平面内的 一条直线，则这条直线平行于这个平面。
4.面面平行判定定理： 若一个平面内有两条相交直线都平行于 另一个平面，则这两个平面平行。
AB' AB BB' b a BC' BA AC CC ' c a b
向量法
2.练习： 在三棱柱ABC A ' B ' C '中，
C' A'
B'
底面是正三角形，AA ' 底面ABC， A ' C AB ', 求证：BC ' AB ' 0 A ' C AB ' (c a ) (b a ) C 2 cb ca a b a A 2 1 a c b 2 BC' AB' (c a b ) ( b a ) (c a 2a b) (b a) (2a b) (b a) 2 2 2 2 2a a b b 2a b 1 1 0
用向量讨论平行与垂直

用向量研究平行关系与垂直关系课件

用向量研究平行关系与垂直关系课件
用向量研究
平行关系与垂直关系
2021.3.15
用向量研究
平行关系与垂直关系
立体几何 演绎体系
用向量刻画两个基本图形及其基本位置关系（平行与垂直）
1. 如何用向量刻画空间中的一条直线？ 2. 如何用向量刻画空间中的一个平面？
用向量研究平行关系与垂直关系
（1）用向量刻画直线动态图 转白板
（2）用向量刻画平面动态图 （其一）
谢谢大家
用向量研究平行关系与垂直关系
现实中的几何模型问题
现
欧氏几何中定理的证明
实
生
活
中
的
物
理
问
题
课后作业 给出几何语言：
（1）两点确定一条直线. （2）不共线三点确定一个平面. （3）过一点有且仅有一个平面和已知直线垂直.
请大家思考如何用量法的特点？
用向量研究平行关系与垂直关系
用向量研究平行关系与垂直关系
向量运用——欧氏几何中定理的证明 问题1：证明“线面垂直判定定理”
一条直线与一个平面内两条相交直线都垂直，则该直线与这个平面垂直. l
AB
用向量研究平行关系与垂直关系
向量运用——欧氏几何中定理的证明 问题1：证明“线面垂直判定定理”
一条直线与一个平面内两条相交直线都垂直，则该直线与这个平面垂直.
（3）用向量刻画平面动态图 （其二）
（4）用向量刻画平面动态图 （其一/借助长方体）
用向量刻画两个基本图形及其基本位置关系（平行与垂直）
两条直线平行的充要条件是它们的方向向量互相平行. 两条直线垂直的充要条件是它们的方向向量互相垂直. 一条直线与一个平面平行或一条直线在一个平面内的充要条件是这条直线的方向向量和 这个平面的法向量互相垂直. 一条直线与一个平面垂直的充要条件是这条直线的方向向量和这个平面的法向量互相平行. 两个平面平行的充要条件是它们的法向量互相平行. 两个平面互相垂直的充要条件是这两个平面的法向量互相垂直.

4 用向量讨论垂直与平行 课件

4 用向量讨论垂直与平行 课件
u // v u v 点击
（2）垂直关系

设直线l，m的方向向量分别为a ，b ，
平面 ，
线线垂直 线面垂直 面面垂直
的法向量分 别为 u，v
l m a b a b 0点击
l


au// uvau
u 点击
v 0
点击
例1（线面垂直判定定理）若一条直线垂直于一个平面内的 两条相交直线，则该直线与此平面垂直.
证明：如图，b, c是平面内的两条相交直线， 直线a满足a b,a c,设p是平面内的任意 一条直线，则只需证a p. 设a,b,c, p的方向向量分别是a,b,c, p,只需证a p.
B'
C'
底面是正三角形，AA' 底面ABC，
A'
A'C AB ',求证：BC ' AB '
设底面边长为2,高为h, 坐标法
如图建立空间直角坐标系.
C
B
A
A( 3,0,0), B(0,1,0),C(0,1,0).
A'( 3,0, h), B'(0,1, h),C'(0,1, h).
AB ' ( 3,1, h), A'C ( 3, 1, h), BC ' (0, 2, h)
例1: 如图已知四边形ABCD、
E
ABEF为两个正方形,
MN分别在其对角线BF上,
FM
B
C
且FM AN.求证：MN // 平面EBC
N
A
D
例2.在正方形ABCD - A1B1C1D1中, 求证 : 平面A1BD // 平面CB1D1
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
E Z
F X
Y
12
练习： 在三棱柱ABC A ' B ' C '中， A ' C AB ', 求证：BC ' AB '
C' A'
B'
底面是正三角形，AA ' 底面ABC，
证明：设底面边长为1, 设a AA', b AB, c AC a b 0, a c 0, b c 1 / 2. A' C A' A AC c a
9
Y
（二）用向量处理垂直问题 例3 : 在正方体ABCD A ' B ' C ' D '中. E,F分别是CC ', BD的中点. 求证：A ' F 平面BDE.
证明:如图 取 DA, DC , DD '分别为x轴,y轴,z轴 X 建立空间直角坐标系, 设正方体的棱长为2.
7
例2.在正方形ABCD - A B1C1 D1中, 1 求证 : 平面A BD // 平面CB1 D1 1
三边所在的直线为x, y, z轴建立空间 A 直角坐标系.设正方体的棱长为1,
则A1 (1, 0, 0), B1 (1,1, 0),
X Z
D
证明 : 如图分别以D1 A1、D1C1、D1 D
Z
E
F
Y
A(2,0,0),B(2,2,0),A '(2,0,2),E(0,2,1),F(1,1,0) 10
例3 : 在正方体ABCD A ' B ' C' D' 中. E,F分别是CC ', BD的中点.
Z
求证：A ' F 平面BDE. A ' F ( 1,1, 2), F Y DB (2,2,0), DE (0,2,1) A ' F DB ( 1,1, (2,2,0) 0, X 2) A ' F DE ( 1,1, (0,2,1) 0 2) A ' F DB, A' F DE, 又DB DE D A F 平面BDE . '

20
l
a
l
b
l m a b a b 0
a
u
m
l a // u a u

u
v
u v u v 0
21

利用向量解决平行与垂直问题
1
一、复习
1、用空间向量解决立体几何问题的“三步曲”
（1）建立立体图形与空间向量的联系，用空间向量表示问题 中涉及的点、直线、平面，把立体几何问题转化为向量问题； （化为 向量问题） （2）通过向量运算，研究点、直线、平面之间的位置关系以及 它们之间距离和夹角等问题； （进行向量运算） （回到图形 （3）把向量的运算结果“翻译”成相应的几何意义。 问题）
2
2、平行与垂直关系的向量表示
设直线l，m的方向向量分别为 a b ， ， 平面 ， 的法向量分别为 u ， v
线线平行 l // m a // b a b 线面平行 l // a u a u 0 面面平行 // u // v u v
14
练习： 在三棱柱ABC A ' B ' C '中， 底面是正三角形，AA ' 底面ABC， A ' C AB ', 求证：BC ' AB '
设底面边长为2, 高为h, 如图建立空间直角坐标系. A( 3 ,0,0), B(0,1,0), C (0,1,0).
坐标法
C
C' A'
B'
B A
A' ( 3 ,0, h), B' (0,1, h), C ' (0,1, h). AB ' ( 3,1, h), A ' C ( 3, 1, h), BC ' (0, 2, h) 0 AB ' A ' C 3 1 h 2 , h 2 2. 2 AB ' BC ' 0 2 h 0. BC ' AB '
C
B
D1
C1
B1
C (0, 0,1), D (0, 0,1) 则A1 D ( 1, 0,1), B1C ( 1, 0,1) A1 D // B1C.即直线A1 D // B1C，
A1
Y
则A1 D // 平面CB1 D1.同理右证：A1 B // 平面CB1 D1.
B1
17
作业： 如图, 直三棱柱ABC A1 B1C1中, ACB 90 ,
0
AC 1, CB 2, 侧棱AA1 1, 侧面AA1 B1 B的 两条对角线交点为D, B1C1的中点为M . 求证CD 平面BDM
A
A1
D
则CD A1 B 0, CD DM 0. CD A1 B, CD DM . CD 平面BDM .
C
B A
向量法
AB' AB BB ' b a BC ' BA AC CC ' c a b
13
练习： 在三棱柱ABC A ' B ' C '中，
C' A'
B'
底面是正三角形，AA ' 底面ABC， A ' C AB ', 求证：BC ' AB ' 0 A ' C AB ' (c a) (b a) 2 c b c a a b a 2 1 a c b 2
4
（2）垂直关系
二、新课
（一）用向量处理平行问题
（二）用向量处理垂直问题
5
（一）用向量处理平行问题
例1: 如图已知四边形ABCD、 ABEF 为两个正方形, MN 分别在其对角线BF 上,
F M E
B
C
N 且FM AN .求证：MN // 平面EBC A 证明 : 在正方形ABCD与ABEF中, D BE AB, FM AN , , FB AC 存在实数 , 使FM FB, AN AC. MN MF FA AN BF EB AC ( BE BA AB AD) EB ( BE AD) EB ( BE BC ) BE ( 1) BE BC.
6
例1: 如图已知四边形ABCD、 ABEF 为两个正方形, MN 分别在其对角线BF 上,
F M
E
B
N
C
且FM AN .求证：MN // 平面EBC MN、 、 共面. BE BC
A
D
M 平面EBC , MN // 平面EBC
评注： 向量p与两个不共线的向量a、b共面的充要条件是 存在实数对x,y使p=xa+yb. 利用共面向量定理可以证明线面平行问题。 本题用的就是向量法。
C
B A
BC ' AB' (c a b) (b a) (c a 2a b) (b a) (2a b) (b a) 2 2 2 2 2 a a b b 2a b 1 1 0
A
A1
解: 如图,以C为原点建立空间直角坐标系. B( 2 ,0,0), B1 ( 2,1,0), A1 (0,1,1),
C
D
C1
M
B 2 1 1 2 D( , , ), M ( ,1,0), 2 2 2 2 2 1 1 1 1 CD ( , , ), A1B ( 2, 1, 1)， (0, , ), DM 2 2 2 2 2
15
三、小结
利用向量解决平行与垂直问题 向量法：利用向量的概念技巧运算解决问 题。 坐标法：利用数及其运算解决问题。 两种方法经常结合起来使用。
16
四 、 作 业
作业： 如图, 直三棱柱ABC A1 B1C1中, ACB 90 ,
0
AC 1, CB 2, 侧棱AA1 1, 侧面AA1 B1 B的 两条对角线交点为D, B1C1的中点为M . 求证CD 平面BDM
8
平面A1 BD // 平面CB1 D1.
例2.在正方形ABCD - A B1C1 D1中, 1 求证 : 平面A BD // 平面CB1 D1 1
D A B Z
C
C1
D1ห้องสมุดไป่ตู้
评注： A1 B1 X 由于三种平行关系可以相互转化， 所以本题可用逻辑推理来证明。 用向量法将逻辑论证转化为问题的算法化， 在应用向量法时需要合理建立空间直角坐标系， 方能减少运算量。本题选用了坐标法。
3
（1）平行关系
设直线l，m的方向向量分别为 a b ， ， 平面 ， 的法向量分别为 u ， v
线线垂直 l m a b a b 0 线面垂直 l a // u a u 面面垂直 u v u v 0
B
C
C1
M
A1 B, DM 为平面BDM内的两条相交直线,
18
B1
教后反思