全等三角形分级练习 第2级 条件转化

二次全等过程训练（一）1.已知：如图，∠A=∠D=90°，AE=DE．求证：△ABC≌△DCB．2.已知：如图，AD=BC，AC=BD．求证：△AOD≌△BOC．3. 3.已知:如图，AB=EF，BC=FG，AC=EG，D为BC中点，H为FG中点．求证：AD=EH．4.已知：如图，四边形ABCD的对角线AC，BD相交于点O，∠1=∠2，∠3=∠4．求证：△ABO≌△ADO．5.已知：如图，AB=AC，DB=DC，F是AD延长线上的一点．求证：△ABF≌△ACF．6.已知：如图，∠E=∠D，AM=CN，ME=ND．求证：△ABE≌△CBD．二次全等过程训练（二）一、单选题1.已知：如图，AD∥BC，AB，CD相交于点O，AO=BO，过点O作EF交AD于点E，交CB 于点F．求证：△EOD≌△FOC．2.已知：如图，AD平分∠BAC，DE⊥AB于E，DF⊥AC于F，且BD=CD．求证：Rt△DEB≌Rt△DFC．3.已知：如图，在四边形ABCD中，AB=CD，AB∥CD，E，F分别是DA，BC延长线上的点，且AE=CF，连接EF交BD于点O．求证：△EOD≌△FOB．4.已知：如图，点C，D在线段BE上，且BD=EC，CA⊥AB于A，DF⊥EF于F，且AB=EF．求证：△ABD≌△FEC．5.如图，在Rt△AEB和Rt△AFC中，∠E=∠F=90°，AB=AC．BE与AC相交于点M，与CF相交于点D，AB与CF相交于点N，∠EAC=∠FAB．求证：△EAM≌△FAN．二次全等过程训练（三）1.已知：如图，在△ABC中，AD平分∠BAC，点D是BC的中点，DF⊥AB于F，DE⊥AC于E．求证：△BDF≌△CDE．2.已知：如图，点A，E，F，C在同一直线上，AE=CF，过点E，F分别作DE⊥AC，BF⊥AC，连接AB，CD，BD，BD交AC于点G，AB=CD．求证：△DEG≌△BFG．3.已知：如图，在Rt△ACD中，∠ADC=90°，BE⊥AC于E，交CD于点F，AE=AD．求证：△CEF≌△BDF．4.已知：如图，在四边形ABCD中，AB=BC=CD=AD，BD平分∠ABC，E为BD上任意一点，连接AE，CE．求证：△ADE≌△CDE．55..已知：如图，在△ABC中，∠ACB=∠ABC=60°，∠EDF=60°，BD=CD，∠DBC=∠DCB=30°，∠BDC=120°，延长AC到点G，使CG=BE．求证：△EFD≌△GFD．二次全等过程训练（四）1.已知：如图，点A，C在直线EF上，BC=AD，AB=CD，AE=CF．求证：∠E=∠F．2.已知，如图，AE=BF，AD=BC，CE=DF．求证：AO=BO．已知：如图，∠D=∠E，AM=ME=CN=DN．试猜想AB和BC的数量关系，并证明你的猜想．4.已知：如图，在△ABC中，点D是BC的中点，DF⊥AB于F，DE⊥AC于E，DF=DE．求证：AB=AC．5.如图，在正方形ABCD中，∠ABC=∠BCD=90°，AB=BC=CD=AD．E为BC边上一点，且AE=DE，AE与对角线BD交于点F，∠ABF=∠CBF，连接CF交DE于点G．求证：DE⊥CF．。

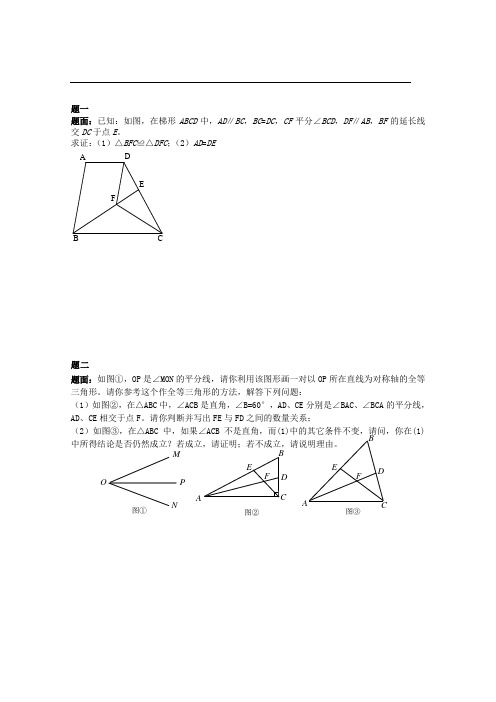
题一题面：已知：如图，在梯形ABCD 中，AD ∥BC ，BC =DC ，CF 平分∠BCD ，DF ∥AB ，BF 的延长线交DC 于点E 。

求证：（1）△BFC ≌△DFC ；（2）AD =DE题二题面：如图①，OP 是∠MON 的平分线，请你利用该图形画一对以OP 所在直线为对称轴的全等三角形。

请你参考这个作全等三角形的方法，解答下列问题：（1）如图②，在△ABC 中，∠ACB 是直角，∠B=60°，AD 、CE 分别是∠BAC 、∠BCA 的平分线，AD 、CE 相交于点F 。

请你判断并写出FE 与FD 之间的数量关系；（2）如图③，在△ABC 中，如果∠ACB 不是直角，而(1)中的其它条件不变，请问，你在(1)中所得结论是否仍然成立？若成立，请证明；若不成立，请说明理由。

O P AM N E B C DF A E F BD图① 图② 图③题三题面：我们知道，两边及其中一边的对角分别对应相等的两个三角形不一定全等。

那么在什么情况下，它们会全等?(1)阅读与证明：对于这两个三角形均为直角三角形，显然它们全等．对于这两个三角形均为钝角三角形，可证它们全等(证明略)．对于这两个三角形均为锐角三角形，它们也全等，可证明如下：已知：△ABC、△A1B1C1均为锐角三角形，AB=A1B1，BC=B1C l，∠C=∠C l。

求证：△ABC≌△A1B1C1。

(请你将下列证明过程补充完整。

)证明：分别过点B，B1作BD⊥CA于D，B1 D1⊥C1 A1于D1.则∠BDC=∠B1D1C1=90°，∵BC=B1C1，∠C=∠C1，∴△BCD≌△B1C1D1，∴BD=B1D1．(2)归纳与叙述：由(1)可得到一个正确结论，请你写出这个结论。

题四题面：下列4个判断：（1）有两边及其中一边上的高对应相等的两个三角形全等；（2）有两边及第三边上的高对应相等的两个三角形全等；（3）三角形6个边、角元素中，有5个元素分别相等的两个三角形全等；（4）一边及其他两边上的高对应相等的两个三角形全等。

1.3探索三角形全等的条件（一~三）【推本溯源】1.由上一节课我们已经知道了全等三角形的性质，它们的对应边相等、对应角相等；那当两个三角形的角和边具备什么样的条件时，两个三角形就相等呢？想一想：（1）当两个三角形的1对边或角相等时，它们全等吗？（2）当两个三角形的2对边或角分别相等时，它们全等吗？（3）当两个三角形的3对边或角分别相等时，它们全等吗？动手做一做：按下列作法，用直尺和圆规作△ABC ，使∠A ＝∠α，AB ＝a ，AC＝b ．作法：1．作∠MAN ＝∠α．2．在射线AM 、AN 上分别作线段AB ＝a ，AC ＝b ．3．连接BC ，△ABC 就是所求作的三角形．通过自己实践后发现：两边及其夹角分别相等的两个三角形全等（简写成“边角边”或“SAS ”）几何语言：∵在△ABC 和△DEF 中，AB＝DE，∠B＝∠E，BC＝EF，∴△ABC ≌△DEF（SAS）．2.用纸板挡住了三角形的一部分，小明根据所学知识很快就画出了一个与原来完全一样的三角形，他的原理是什么？ba D E FC B A动手做一做：按下列作法，用圆规和直尺作△ABC ，使AB ＝a ，∠A ＝∠α，∠B ＝∠β．（1）作AB ＝a ．（2）在AB 的同一侧分别作∠MAB ＝∠α，∠NBA ＝∠β，AM 、BN 相交于点C ．△ABC 就是所求作的三角形．通过自己实践后发现：两角及其夹边分别相等的两个三角形全等（简写成“角边角”或“ASA ”）几何语言：∵在△ABC 和△DEF 中，∠A＝∠D，AB＝DE，∠B＝∠E，∴△ABC ≌△DEF（ASA）．【解惑】例1：如图，为测量池塘两侧A ，B 两点间距离，在地面上找一点C ，连接AC ，BC ，使90ACB ∠=︒，然后在AC 的延长线上确定点D ，使CD AC =，得到ABC DBC ≌△△，通过测量BD 的长，就能得出AB 的长．那么ABC DBC ≌△△的理由是（）D E FC B AA ．SASB ．ASAC ．AASD ．SSS【答案】A 【分析】根据已知条件可找到两边对应相等且夹角相等，利用SAS 即可证明ABC DBC ≌△△，由此即可解决问题．【详解】解：∵90ACB ∠=︒，∴90DCB ACB ∠=∠=︒，则在ABC 和DBC △中90DC AC DCB ACB BC BC =⎧⎪∠=∠=︒⎨⎪=⎩∴()SAS ABC DBC ≌ ．故选：A ．【点睛】本题考查全等三角形的应用，解题的关键是熟练掌握全等三角形的判定方法，属于中考常考题型．例2：如图，C ，A ，D 三点在同一直线上，AB CE ∥，AB CD =，AC CE =．求证：ABC ≌CDE ．【答案】见解析【分析】由平行线的性质得到BAC DCE ∠=∠，由SAS 即可证明ABC ≌()SAS CDE ．【详解】解：AB CE ∥ ，BAC DCE ∴∠=∠，在ABC 和CDE 中，AB CD BAC DCE AC CE =⎧⎪∠=∠⎨⎪=⎩，ABC ∴ ≌()SAS CDE ．【点睛】本题考查全等三角形的判定，关键是掌握全等三角形的判定方法．例3：如图，要测量河两岸相对的两点A 、B 的距离，先在AB 的垂线BF 上取两点C 、D ，使CD BC =，再定出BF 的垂线DE ，可以证明EDC ABC ≌，得ED AB =，因此，测得ED 的长就是AB 的长．判定EDC ABC ≌的理由是（）A ．SSSB ．ASAC ．AASD ．SAS【答案】B 【分析】由已知可以得到ABC BDE ∠=∠，又CD BC =，ACB DCE ∠=∠，由此根据角边角即可判定EDC ABC ≌．【详解】解：BF AB ⊥ ，DE BD ⊥,ABC BDE ∴∠=∠,又CD BC = ，ACB DCE ∠=∠,EDC ABC ∴ ≌（ASA ）故选：B ．【点睛】本题主要考查了三角形全等的判定定理，熟练掌握三角形全等的判定定理是解题的关键．例4：如图，C E ∠=∠，点D 在BC 边上，BC DE =，12∠=∠，AC 和DE 相交于点O ．求证：ABC ADE △≌△．【答案】见解析【分析】先利用三角形外角性质证明ADE B ∠=∠，然后根据“ASA ”判断ABC ADE △≌△．【详解】证明：1ADC B ∠=∠+∠ ，即21ADE B ∠+∠=∠+∠，而12∠=∠，ADE B ∴∠=∠，在ABC 和ADE V 中，C E BC DE B ADE ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)ABC ADE ∴ ≌．【点睛】本题考查了全等三角形的判定：熟练掌握全等三角形的5种判定方法．选用哪一种方法，取决于题目中的已知条件，若已知两边对应相等，则找它们的夹角或第三边；若已知两角对应相等，则必须再找一组对边对应相等，且要是两角的夹边，若已知一边一角，则找另一组角，或找这个角的另一组对应邻边．例5：在ABC 中，AC BC =，90ACB ∠=︒，D 是射线BA 上一动点，连接CD ，以CD 为边作45DCE ∠=︒，CE 在CD 右侧，CE 与过点A 且垂直于AB 的直线交于点E ，连接DE ．(1)当CD CE ，都在AC 的左侧时，如图①，线段BD AE DE ，，之间的数量关系是_________；(2)当CD CE ，在AC 的两侧时，如图②，线段BD AE DE ，，之间有怎样的数量关系？写出你的猜想，并给予证明；(3)当CD CE ，都在AC 的右侧时，如图③，线段BD AE DE ，，之间有怎样的数量关系？直接写出你的猜想，不必证明．【答案】(1)BD AE DE+=(2)BD AE DE -=，详见解析(3)BD AE DE-=【分析】（1）过点C 作CF CE ⊥，交AB 延长线于点F ，如图，先证明CBF CAE ≌，得到BF AE =，CF CE =，然后证明DCE DCF ≌解题即可；（2）过点C 作CF CE ⊥，交AB 于点F ，如图，先证明CBF CAE ≌，得到BF AE =，CF CE =，然后证明DCE DCF ≌解题即可；（3）过点C 作CF CE ⊥，交AB 于点F ，如图，先证明CBF CAE ≌，得到BF AE =，CF CE =，然后证明DCE DCF ≌解题即可；【详解】（1）过点C 作CF CE ⊥，交AB 延长线于点F ，如图．∴90ECF ACB ∠=∠=︒．∴FCB ECA ∠=∠．∵AE AB ⊥，∴90EAB ∠=︒．∵45CBA CAB ∠=∠=︒，∴135CBF CAE ∠=∠=︒．∵BC AC =，∴(ASA)CBF CAE ≌．∴BF AE =，CF CE =．∵45DCE ∠=︒，90ECF ∠=︒，∴45DCE DCF ∠=∠=︒．∵CD CD =，∴()SAS DCE DCF ≌．∴DE DF =．∵BD BF DF +=，∴BD AE DE +=．故答案为：BD AE DE +=．（2）图②的猜想：BD AE DE -=．证明：过点C 作CF CE ⊥，交AB 于点F ，如图②．∴90ECF ACB ∠=∠=︒．∴CBF CAE ∠=∠．∵AE AB ⊥，∴90EAB ∠=︒．∵45CBA CAB ∠=∠=︒，∴45CBF CAE ∠=∠=︒．∵BC AC =，∴(ASA)CBF CAE ≌．∴BF AE =，CF CE =．∵45DCE ∠=︒，90ECF ∠=︒，∴45DCE DCF ∠=∠=︒．∵CD CD =，∴()SAS DCE DCF ≌．∴DE DF =．∵BD BF DF -=，∴BD AE DE -=．（3）过点C 作CF CE ⊥，交AB 于点F ，如图∴90ECF ACB ∠=∠=︒．∴FCB ECA ∠=∠．∵AE AB ⊥，∴90EAB ∠=︒．∵45CBA CAB ∠=∠=︒，∴45CBF CAE ∠=∠=︒．∵BC AC =，∴(ASA)CBF CAE ≌．∴BF AE =，CF CE =．∵45DCE ∠=︒，90ECF ∠=︒，∴45DCE DCF ∠=∠=︒．∵CD CD =，∴()SAS DCE DCF ≌．∴DE DF =．∵BD BF DF -=，∴BD AE DE -=．故答案为：BD AE DE -=．【点睛】本题考查全等三角形的判定和性质，掌握全等三角形的判定和性质是解题的关键．【摩拳擦掌】1．（2023春·上海徐汇·七年级上海市第二初级中学校考阶段练习）如图，已知12∠=∠，AC AB =，则ABD ACD △≌△的依据是（）A ．ASAB ．AASC ．SSSD ．SAS【答案】D 【分析】根据全等三角形的判定定理可进行求解．【详解】解：在ABD △和ACD 中，12AC AB AD AD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABD ACD ≌△△；故选D ．【点睛】本题主要考查全等三角形的判定，熟练掌握全等三角形的判定是解题的关键．2．（2023·四川成都·统考二模）如图，AB 与CD 相交于点O ，且O 是AB CD ，的中点，则AOC 与BOD 全等的理由是（）A ．SASB ．ASAC ．SSSD ．HL【答案】A 【分析】根据全等三角形的判定定理求解即可．【详解】解：∵O 是AB CD ，的中点，∴,,OA OB OC OD ==在AOC 和DOB 中，OA OB AOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩∴()SAS AOC DOB ≅ ，故选：A ．【点睛】此题考查了全等三角形的判定，熟记全等三角形的判定定理是解题的关键．3．（2022秋·七年级单元测试）如图，为了测量B 点到河对面的目标A 之间的距离，在B 点同侧选择一点C ，测得75ABC ∠=︒，35ACB ∠=︒，然后在M 处立了标杆，使75MBC ∠=︒，35MCB ∠=︒，得到MBC ABC ≌△△，测得MB 的长就是A ，B 两点间的距离，这里判定MBC ABC ≌△△的理由是（）A ．SSSB ．SASC ．ASAD ．AAA【答案】C 【分析】利用全等三角形的判定方法进行分析即可．【详解】解：在MBC 和ABC 中，MBC ABC BC BC MCB ACB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA MBC ABC ≌，∴判定MBC ABC ≌△△的理由是ASA ，故选：C ．【点睛】本题考查全等三角形判定的实际应用，是重要考点，掌握相关知识是解题关键．4．（2022秋·云南楚雄·八年级校考阶段练习）如图，小亮书上的三角形被墨迹污染了一部分，很快他就根据所学知识画出一个与书上完全一样的三角形，那么这两个三角形完全一样的依据是（）A ．SSSB ．SASC ．AASD ．ASA【答案】D 【分析】观察图形可知，有两角以及两角的夹边是已知，由此即可得到答案．【详解】解：由题意得，有两角以及两角的夹边是已知，因此可以利用ASA 画出一个全等的三角形，故答案为：ASA故选D【点睛】本题主要考查了全等三角形的判定，熟知全等三角形的判定条件是解题的关键．5．（2023春·广东惠州·八年级校考阶段练习）如图，ABC 中，AB AC =，AD 平分BAC ∠，则_____≌_____．【答案】BAD CAD【分析】直接利用全等三角形的判定方法()SAS ，进而得出答案．【详解】解：∵AD 平分BAC ∠，∴BAD CAD ∠=∠，在BAD 和CAD 中,AB AC BAD CAD AD AD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BAD CAD ≌．故答案为：BAD ，CAD ．【点睛】此题主要考查了全等三角形的判定，熟练掌握全等三角形的判定方法是解题关键．6.（2023秋·吉林长春·八年级统考期末）如图，把两根钢条的中点连在一起，可以做成一个测量工件内槽的工具（卡钳）．在图中，若测量得20cm A B ''=，则工件内槽宽AB =_________cm ．【答案】20【分析】根据三角形全等的判定可知()SAS ≌AOB A OB ''△△，从而得到20cm AB A B ''==．【详解】解：由题意可知，()SAS ≌AOB A OB ''△△，∴20cm AB A B ''==，故答案为：20．【点睛】本题考查全等三角形的应用，熟记全等三角形的判定与性质是解决问题的关键．7．（2023春·陕西咸阳·七年级咸阳市实验中学校考阶段练习）如图，在ABC 中，AD 是BC 上的中线，点F 、E 分別在AD 和AD 的延长线上，且DE DF =，连接BE 、CF ．试说明：BE CF ∥．【答案】见解析【分析】证明BDE CDF ≌得到EBD FCD Ð=Ð得证BE CF ∥．【详解】解：∵AD 是BC 上的中线，∴BD DC =，∵在BDE 和CDF 中DE DF BDE CDF BD CD =⎧⎪∠=∠⎨⎪=⎩，∴()SAS BDE CDF △≌△，∴EBD FCD Ð=Ð，∴BE CF ∥．【点睛】本题考查了三角形全等的判定和性质，平行线的判定定理，熟练掌握全等的判定，8．（2023·广东广州·统考二模）为了制作燕子风筝，燕子风筝的骨架图如图所示，AB AE =，AC AD =，BAD EAC ∠=∠，证明：A ABC ED ≌△△．【答案】见解析【分析】根据SAS 证明A ABC ED ≌△△即可．【详解】证明：∵BAD EAC ∠=∠，∴BAD CAD EAC CAD ∠+∠=∠+∠，∴BAC EAD ∠=∠，∴在ABC 和AED △中，AB AE BAC EAD AC AD =⎧⎪∠=∠⎨⎪=⎩∴()SAS ABC AED ≌【点睛】此题考查了三角形全等的判定方法，解题的关键是熟练掌握三角形全等的判定方法．9．（2023春·陕西西安·七年级西安市远东第二中学校考阶段练习）如图，小刚站在河边的A 点处，在河对岸的B 处有一电线塔（小刚的正北方向），他想知道电线塔离他有多远，于是他向正西方向走了20步到达一棵树C 处，接着再向前走了20步到达D 处，然后再左转90︒直行，当小刚看到电线塔B 、树C 与自己现处的位置E 在一条直线时，他共走了120步.(1)根据题意，画出示意图；(2)若小刚一步约0.5米，请求出A 、B 两点间的距离（写出推理过程）.【答案】(1)见解析(2)40米，见解析【分析】（1）根据上北下南，左西右东，直角的意义，共线的条件画图即可．（2）根据三角形全等，得到120202080AB DE ==--=步，结合一步约0.5米，代入计算即可．【详解】（1）根据上北下南，左西右东，直角的意义，共线的条件画图如下：则画图即为所求．（2）∵ACB DCE AC CD BAC EDC ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA ACB DCE ≌，∴120202080AB DE ==--=步，∵一步约0.5米，∴800.540AB =⨯=（米），答：A 、B 两点间的距离约为40米．【点睛】本题考查了三角形全等的判定和性质，熟练掌握三角形全等的判定的应用是解题的关键．10．（2023·云南楚雄·统考三模）如图，AE 和BD 相交于点C ，AB DE ∥，AB ED =．求证：AC EC =．【答案】见解析【分析】由平行线的性质可得B D ∠=∠，A E ∠=∠．根据ASA 证明ABC EDC △△≌，即可推出AC EC =．【详解】证明：∵AB DE ∥，∴B D ∠=∠，A E ∠=∠．在ABC 和EDC △中，B D AB ED A E ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ASA ABC EDC ≌△△．∴AC EC =．【点睛】本题考查全等三角形的判定与性质，解题的关键是熟练掌握全等三角形的判定方法．【知不足】1．（2023春·全国·七年级专题练习）如图，12m AB =，CA AB ⊥于点A ，DB AB ⊥于点B ，且4m AC =，点P 从B 向A 运动．每分钟走1m ，点Q 从B 向D 运动，每分钟走2m ，P 、Q 两点同时出发，运动（）分钟后，CAP 与PQB △全等．A ．2或4B ．3C ．4D ．4或6【答案】C 【分析】设运动x 分钟后CAP 与PQB △全等，则m BP x =，2m BQ x =，(12)m AP x =-，分两种情况：①若BP AC =，则4x =，此时AP BQ =，CAP PBQ ≌△△；②若BP AP =，则12x x -=，得出6x =，12BQ AC =≠，此情况舍去，则得出结果．【详解】解：∵CA AB ⊥于A ，DB AB ⊥于B ，∴90A B ∠=∠=︒．设运动x 分钟后CAP 与PQB △全等，则m BP x =，2m BQ x =，(12)m AP x =-，分类讨论：①若BP AC =，则4x =，∴12488AP BQ AP BQ =-===，，，∴(SAS)CAP PBQ ≌；②若BP AP =，则12x x -=，解得：6x =，∴12BQ AC =≠，此时CAP 与PQB △不全等；综上所述：运动4分钟后CAP 与PQB △全等；故选C ．【点睛】本题考查三角形全等的判定方法、解方程等知识；本题难度适中，利用分类讨论的思想是解题关键．2．（2023秋·八年级单元测试）如图，一块三角形的玻璃破成三片，一位同学很快拿着其中一片玻璃说：根据所学知识就能配出一个与原三角形完全一样的图形．他这样做的依据是（）A ．SSSB ．SASC ．AASD ．ASA【答案】D 【分析】结合三角形全等的判定条件，依次对三片玻璃进行分析即可．【详解】解：第一片玻璃只有一个角与原三角形相等，无法判断与原三角形全等；第二片玻璃既没有边与原三角形相等，也有没有角与原三角形相等，无法判断与原三角形全等；第三片玻璃有两角及其夹边与原三角形相等，可以通过ASA 判定新三角形与原三角形全等；故选：D ．【点睛】本题考查三角形全等的判定条件，解题的关键是熟练掌握三角形全等的相关知识．3．（2023春·全国·七年级专题练习）小刚把一块三角形玻璃打碎成了如图所示的三块，现要到玻璃店取配一块完全一样的玻璃，那么最省事的办法是（）A ．带①去B ．带②去C ．带③去D ．带①和②去【答案】C 【分析】根据三角形全等的条件进行判断即可．【详解】解：第一块和第二块只保留了原三角形的一个角和部分边，根据这两块中的任一块均不能配一块与原来完全一样的；第三块不仅保留了原来三角形的两个角还保留了一边，则可以根据ASA 来配一块一样的玻璃，应带③去．故选：C ．【点睛】本题主要考查全等三角形的应用，熟练掌握全等三角形的判定定理是解题的关键．4．（2023春·全国·七年级专题练习）ABC 中，8AC =，BC 边上的中线6AD =，则边AB 的取值范围是__．【答案】420AB <<【分析】延长AD 至E 使DE AD =，连接CE ，然后证明ADB EDC ≅ ，接着利用三角形的三边关系即可得到AB 的取值范围．【详解】延长AD 至E 使DE AD =，连接CE在ADB 和EDC 中，AD ED ADB CDE BD CD =⎧⎪∠=∠⎨⎪=⎩ADB EDC∴≅ AB CE∴=8AC = ，212AE AD ==420AE AC CE AC AE ∴-=<<+=420AB ∴<<．故答案为：420AB <<．【点睛】本题考查了全等三角形的判定与性质以及三角形的三边关系，正确的作出辅助线是解题的关键．5．（2021春·广东河源·七年级统考期末）如图，在ABC 和DEF 中，AB DE ∥，AB DE =，点A ，F ，C ，D 在同一条直线上且AF DC =．请说明ABC DEF ≌△△．【答案】见解析【分析】由平行线的性质可得A D ∠=∠，由AF DC =，可得AC DF =，进而根据SAS 即可证明ABC DEF ≌△△．【详解】证明： AB DE ∥，∴A D ∠=∠，AF DC =，∴AFFC DC FC +=+，即AC DF =，在ABC 和DEF 中，AC DF A D AB DE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABC DEF △△≌．【点睛】本题考查全等三角形的判定、平行线的性质，解题的关键是熟练掌握全等三角形的判定方法．6．（2023·云南昆明·统考一模）如图，点A 、B 、C 、D 在同一直线上，AF DE =，A D ∠=∠，AC DB =．求证：ABF DCE △△≌．【答案】见解析【分析】利用线段的加减证得AB DC =，即可用“SAS ”证明三角形全等．【详解】证明：∵AC DB =，∴AC BC DB BC -=-，即AB DC =，在ABF △和DCE △中，∵AF DE A D AB DC =⎧⎪∠=∠⎨⎪=⎩，∴(SAS)ABF DCE ≌△△．【点睛】本题考查的是三角形全等的判定，掌握三角形的各个判定定理是关键．7．（2023·云南昭通·统考二模）如图，点A ，F ，C ，D 在同一直线上，BC EF ∥，AF DC =，BC EF =．求证：ABC DEF ≌△△．【答案】见解析【分析】根据平行线的性质可得ACB DFE ∠=∠，再由AF CD =，可得AC DF =，再根据全等三角形的判定即可得出结论．【详解】证明：BC EF ∥，ACB DFE ∴∠=∠，AF CD = ，AC DF =∴，在ABC 和DEF 中，AC DF ACB DFE BC EF =⎧⎪∠=∠⎨⎪=⎩(SAS)ABC DEF ∴△≌△．【点睛】本题考查平行线的性质和全等三角形的判定，熟练掌握全等三角形的判定是解题的关键．8．（2023·云南昆明·统考二模）“倍长中线法”是解决几何问题的重要方法．所谓倍长中线法，就是将三角形的中线延长一倍，以便构造出全等三角形，具体做法是：如图，AD 是ABC的中线，延长AD 到E ，使DE AD =，连接BE ，构造出BED 和CAD ．求证：BED CAD △≌△．【答案】见解析【分析】由AD 是ABC 的中线，可得DE AD =，再由EDB ADC ∠=∠，DB DC =，即可证明BED CAD △≌△．【详解】证明：如图所示：，AD 是ABC 的中线，DB DC ∴=，在BED 和CAD 中，ED ADEDB ADC DB DC =⎧⎪∠=∠⎨⎪=⎩，(SAS)BED CAD ∴ ≌．【点睛】本题主要考查了三角形全等的判定，倍长中线，熟练掌握三角形全等的判定，添加适当的辅助线是解题的关键．【一览众山小】1．（2023秋·吉林长春·八年级统考期末）如图，在用尺规作图得到DBC ABC ≌过程中，运用的三角形全等的判定方法是（）A ．SASB ．ASAC ．AASD ．SSS【答案】B 【分析】根据作法可得,ABC DBC ACB DCB ∠=∠∠=∠，可利用ASA 证明DBC ABC ≌，即可求解．【详解】解：根据作法得：,ABC DBC ACB DCB ∠=∠∠=∠，∵BC BC =，∴()ASA DBC ABC ≌．故选：B【点睛】本题主要考查了尺规作图——作一个角等于已知角，全等三角形的判定，熟练掌握作一个角等于已知角的作法，全等三角形的判定定理是解题的关键．2．（2023·山东菏泽·统考一模）如图，18m AB =，CA AB ⊥于A ，DB AB ⊥于B ，且6m AC =，点P 从B 向A 运动，每秒钟走1m ，Q 点从B 向D 运动，每秒钟走2m ，点P ，Q 同时出发，运动______秒后，CAP 与PQB △全等．【答案】6【分析】设运动x 秒钟后CAP 与PQB △全等；则m 2m BP x BQ x ＝，＝，则()18m AP x =-，分两种情况：①若BP AC =，则6x =，此时AP BQ =，()SAS CAP PBQ ≌；②若BP AP =，则18x x -=，得出9x =，218BQ x AC ==≠，即可得出结果．【详解】解：∵CA AB ⊥于A ，DB AB ⊥于B ，∴90A B ∠=∠=︒，设运动x 分钟后CAP 与PQB △全等；则m 2m BP x BQ x ＝，＝，则()18m AP x =-，分两种情况：①若BP AC =，则6x =，∴18612AP =-=，12BQ =，AP BQ =，∴()SAS CAP PBQ ≌；②若BP AP =，则18x x -=，解得：9x =，218BQ x AC ==≠，此时CAP 与PQB △不全等；综上所述：运动6秒钟后CAP 与PQB △全等；故答案为：6．【点睛】本题考查了三角形全等的判定方法、解方程等知识；本题难度适中，需要进行分类讨论．3．（2022秋·湖北恩施·八年级校考阶段练习）如图，要测量池塘两端A ，B 的距离，可先在平地上取一个可以直接到达A ，B 两点的点C ，连接AC 并延长AC 到点D ，使CD CA =，连接BC 并延长BC 到点E ，使CE CB =，连接DE ，那么量出DE 的长就等于AB 的长，这是因为ABC DEC ≅ ，而这个判定全等的依据是______（填字母）．【答案】SAS【分析】先根据对顶角相等可得ACB DCE ∠=∠，再根据三角形全等的判定即可得．【详解】解：由对顶角相等得：ACB DCE ∠=∠，在ABC 和DEC 中，CA CD ACB DCE CB CE =⎧⎪∠=∠⎨⎪=⎩，()SAS ABC DEC ∴≅ ，故答案为：SAS ．【点睛】本题考查了三角形全等的判定，熟练掌握三角形全等的判定是解题关键．4．（2023·云南昆明·昆明八中校考三模）如图，点B ，C ，E ，F 在同一条直线上，AB DE =，A D ∠=∠，AC DF =．求证：BF CE =．【答案】见解析【分析】先证明()SAS ABC DEF ≌△△，可得BC EF =，根据BC CF EF FC -=-即可证明．【详解】证明：在ABC 和DEF 中，∵AB DE A D AC DF =⎧⎪∠=∠⎨⎪=⎩，∴()SAS ABC DEF ≌△△，∴BC EF =，∵BC CF EF FC -=-，∴BF CE =．【点睛】本题考查了几何证明，涉及到全等三角形的判定与性质，找出BC CF EF FC -=-是关键．5．（2023秋·八年级课时练习）如图，在ABC 中，点D 是AC 上一点，AD AB =，过点D 作DE AB ∥，且DE AC =，连接AE ，CE ．(1)求证：ABC DAE △≌△；(2)若D 是AC 的中点，ABC 的面积是20，求AEC △的面积．【答案】(1)见解析(2)40【分析】（1）根据两直线平行，内错角相等可得BAC ADE ∠=∠，再利用“边角边”证明即可；（2）根据全等三角形面积相等，即三角形中线的性质即可求解．【详解】（1）证明：DE AB ∥，BAC ADE ∴∠=∠，在ABC 和DAE 中，AB DA BAC ADE AC DE =⎧⎪∠=∠⎨⎪=⎩，()SAS ABC DAE ∴△≌△；（2）解：ABC DAE ≌，20ABC DAE S S ∴==△△．D 是AC 的中点，222040AEC DAE S S ∴==⨯=△△．【点睛】本题主要考查了全等三角形的判定与性质，平行线的性质，三角形的中线将三角形面积平分为两等份，熟记三角形全等的判定方法是解题的关键．6．（2023·浙江·模拟预测）如图，在ABC 中，AC AB >，射线AD 平分BAC ∠，交BC 于点E ，点F 在边AB 的延长线上，AF AC =，连接EF ．(1)求证：AEC AEF ≌．(2)若50AEB ∠=︒，求BEF ∠的度数．【答案】(1)证明见解析(2)80︒【分析】（1）由射线AD 平分BAC ∠，可得CAE FAE ∠=∠，进而可证()SAS AEC AEF ≌；（2）由()SAS AEC AEF ≌，可得C F ∠=∠，由三角形外角的性质可得50AEB CAE C ∠=∠+∠=︒，则50FAE F ∠+∠=︒，根据180FAE F AEB BEF ∠+∠+∠+∠=︒，计算求解即可．【详解】（1）证明：射线AD 平分BAC ∠，∴CAE FAE ∠=∠，在AEC △和AEF △中，∵AC AF CAE FAE AE AE =⎧⎪∠=∠⎨⎪=⎩，∴()SAS AEC AEF ≌；（2）解：∵()SAS AEC AEF ≌，∴C F ∠=∠，∵50AEB CAE C ∠=∠+∠=︒，∴50FAE F ∠+∠=︒，∵180FAE F AEB BEF ∠+∠+∠+∠=︒，∴80BEF ∠=︒，∴BEF ∠为80︒．【点睛】本题考查了角平分线，全等三角形的判定与性质，三角形外角的性质，三角形内角和定理．解题的关键在于对知识的熟练掌握与灵活运用．7．（2022秋·福建泉州·八年级校考阶段练习）如图，在43⨯的正方形网格中，ABC 的顶点都在正方形网格的格点上请你在图①和图②中分别画出一个三角形，同时满足以下两个条件：(1)以点A 为一个顶点，另外两个顶点也在正方形网格点上；(2)与ABC 全等，且不与ABC 重合．【答案】(1)见解析(2)见解析【分析】（1）直接利用网格结合全等三角形的判定方法分析得出答案；（2）直接利用网格结合全等三角形的判定方法分析得出答案．【详解】（1）如图所示：ABD △即为所求；在ABC 和ABD △中453AB AB ABC ABD BC BD =⎧⎪∠=∠=︒⎨⎪==⎩∴()SAS ABC ABD ≌．（2）如图所示：BAE 即为所求．∵AE BC ∥，∴ABC BAE ∠=∠．在ABC 和BAE 中3AB BA ABC BAE BC AE =⎧⎪∠=∠⎨⎪==⎩∴()SAS ABC BAE ≌．【点睛】此题主要考查了应用设计与作图，熟练掌握全等三角形的判定方法是解题关键．8．（2023·云南昆明·校考三模）如图，在ABC 和ADE V 中，C E ∠=∠，AC AE =，CAD EAB ∠=∠．求证：ABC ADE △≌△．【答案】证明见解析；【分析】根据角的和差得到DAE CAB ∠=∠，再根据全等三角形的判定即可解答．【详解】解：∵CAD EAB ∠=∠，∴CAD BAD EAB BAD ∠+∠=∠+∠，∴DAE CAB ∠=∠，∴在ABC 和ADE 中，C E AC AE CAB DAE ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴()ABC ADE ASA ≌；【点睛】本题考查了角的和差关系，全等三角形的判定，掌握全等三角形的判定是解题的关键．9．（2022春·七年级单元测试）如图，A ∠＝B ∠，AE ＝BE ，点D 在AC 边上，1∠＝2∠，AE 和BD 相交于点O ．求证：AEC BED ≌△△．【答案】见解析【分析】利用三角形内角和得到2BEO ∠=∠，结合12∠=∠推出AEC BED ∠=∠，再利用ASA 证明AEC BED △△≌即可．【详解】解：证明：AE 和BD 相交于点O ，AOD BOE ∴∠=∠．在AOD △和BOE △中，A B ∠=∠，2BEO ∴∠=∠．又12∠=∠ ，1BEO ∴∠=∠，AEC BED ∴∠=∠．在AEC △和BED 中，A B AE BE AEC BED ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)AEC BED ∴△≌△．【点睛】本题考查全等三角形的判定，解题的关键是熟练运用全等三角形的性质与判定．10．（2022秋·七年级单元测试）如图，在ABC 中，AB AC =，AD BC ⊥于点D ，CE AB ⊥于点E ，AE CE =，AD 与CE 相交于点F ．求证：AEF CEB ≌．【答案】见解析【分析】由ASA 证明AEF CEB ≌即可．【详解】证明：AD BC ⊥ ，90B BAD ∴∠+∠=︒，CE AB ⊥ ，90B BCE ∴∠+∠=︒，EAF ECB ∴∠=∠，在AEF △和CEB 中，AEF BEC AE CE EAF BCE ∠=∠⎧⎪=⎨⎪∠=∠⎩，(ASA)AEF CEB ∴ ≌．【点睛】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识；熟练掌握等腰三角形的性质，证明三角形全等是解题的关键．11．（2023·辽宁鞍山·统考一模）如图，在ABC 中，AB AC =，CD AB ∥，连接AD ，E 为AC 边上一点，ABE CAD ∠=∠，求证：ABE CAD ≌．【答案】证明见解析【分析】根据CD AB ∥，得到BAE ACD ∠=∠，利用ASA 即可得证．【详解】证朋：CD AB ∥，BAE ACD ∴∠=∠，AB AC = ，ABE CAD ∠=∠，()ASA ABE CAD ∴ ≌．【点睛】本题考查全等三角形的判定．熟练掌握全等三角形的判定方法，是解题的关键．12．（2023秋·湖南常德·八年级统考期末）如图，在ABC 中，90ACB ∠=︒，AC BC =，AE 是BC 边上的中线，过点C 作CF AE ⊥于点F ，过点B 作BD BC ⊥交CF 的延长线于点D ，连接DE ．(1)求证：DBC ECA △≌△；(2)若6AC =，求CDE 的面积．【答案】(1)见解析中，（2）如图2，在ABC∠=∠在线段AD上，12【答案】（1）见解析；【分析】（1）由1∠又由AB AC =即可得到（2）ABC 的面积为的面积＝CAF V 的面积，则可得到结论．【详解】（1）证明：BAC BAE ∠=∠+∴ABE CAF ∠=∠在ABE 和CAF V ABE CAF AB AC BAE ACF ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴ABE CAF ≌△△（2）解：∵ABC ∴ACD 的面积是：由（2）可得ABE △即ABE 的面积＝∴ABE 与CDF 【点睛】此题主要考查了全等三角形的判定和性质，键．求证：ABE CAF V V ≌；若ABC 的面积为18，BD BC 【答案】(1)证明见解析．(2)12．【分析】（1）利用ASA 证明三角形全等即可；判定方法，证明三角形全等是解题的关键．。

2024-2025学年度八年级数学上册探索三角形全等的条件（HL ）专项练习一、单选题（本大题共10小题，每小题3分，共30分）1．（八年级下·山西晋中·期中）如图，已知，，若用“”判定和AB AC ⊥CD AC ⊥HL Rt ABC △全等，则需要添加的条件是（ ）Rt CDA △A ．B ．C ．D ．B D ∠=∠ACB CAD ∠=∠AB CD =AD CB=2．（八年级上·湖北随州·期末）如图，于P ，，添加下列一个条件，能利用“”AC BD ⊥AP CP =HL 判定的条件是（ ）ABP CDP △≌△A ．B ．与互余C ．D ．AB CD B ∠C ∠BP DP =AB CD =3．（八年级上·河南南阳·阶段练习）如图，在和中，，，ABC CDE 90ACB CED ∠=∠=︒AB CD =，则下列结论不一定成立的是（）BC DE =A ．B ．C ．D ．ABC CDE △△≌CE BE =AB CD ⊥CAB ECD=∠∠4．（八年级上·江西抚州·期中）如图，有两个长度相同的滑梯靠在一面墙上．已知，AC DF AB DE ==，则这两个滑梯与地面夹角与的度数和是（ ）ABC ∠DFE ∠A ．B ．C ．D ．60︒90︒120︒150︒5．（八年级上·湖北十堰·阶段练习）如图，有两个长度相同的滑梯，左边滑梯的高度与右边滑梯水AC 平方向的长度相等，若，则（ ）DF 32CBA ∠=︒EFD ∠=A ．B ．C ．D ．42︒58︒52︒48︒6．（20-21八年级上·天津红桥·期中）如图，△ABC 中，点D 是BC 边上一点，DE ⊥AB 于点E ，DF ⊥BC ，且BD =FC ，BE =DC ，∠AFD =155°，则∠EDF 的度数是（ ）A ．50°B ．55°C ．60°D ．65°7．（八年级上·江苏南京·期末）如图，，垂足为，是上一点，且，EC BD ⊥C A EC AC CD =．若，，则的长为（ ）AB DE = 3.5AC =9BD =AEA ．2B ．2.5C ．3D ．5.58．（八年级上·河北张家口·期中）如图，，，，，则CD AD ⊥CB AB ⊥CD CB =100BCD ∠=︒（ ）BAC ∠=A ．30°B ．40°C ．50°D ．60°9．（14-15八年级上·江苏盐城·课后作业）如图，在△ABC 中，∠C =90°，点D 在AB 上，BC =BD ，DE ⊥AB 交AC 于点E ，△ABC 的周长为12，△ADE 的周长为6，则BC 的长为（ ）A ．3B ．4C ．5D ．610．（八年级下·河南平顶山·期中）如图，的高与相交于点，，的延长线ABC BD CE O OD OE =AO 交于点，则图中共有全等的直角三角形（ ）BC MA ．3对B ．4对C ．5对D ．6对二、填空题（本大题共8小题，每小题4分，共32分）11．（八年级上·甘肃平凉·期末）如图，在中，分别是边上的高，已知ABC AD BE 、BC AC 、；若，则的度数为 ．AE BD =60CAB ∠=︒CBE ∠12．（八年级上·河南南阳·期中）如图，在中，，点在上，，ABC 90C ∠=︒D AB BC BD =交于点，的周长为，的周长为，则边的长为 ．DE AB ⊥AC E ABC 12cm ADE 6cm BC cm13．（八年级上·河北保定·阶段练习）如图，有两个长度相同的滑梯，左边滑梯的高度与右边滑梯AC水平方向的长度相等，两个滑梯的倾斜角和的数量关系是 ．DF ABC ∠DFE ∠14．（八年级上·新疆伊犁·期中）如图，于E ，于F ，若，，则下DE AB ⊥DF AC ⊥BD CD =BE CF =列结论：①；②平分；③；④，中正确的是 ．DE DF =AD BAC ∠AE AD =2AC AB BE -=15．（八年级上·江苏南通·阶段练习）如图，E 是的中点，平分，90B C ∠=∠=︒BC DE ADC ∠，则 ．35CED ∠=︒EAB ∠=16．（八年级上·重庆渝中·阶段练习）如图，在四边形中，、为对角线，且，ABCD AC BD AC AB =，于点．若，，则的长度为 ．ACD ABD ∠=∠AE BD ⊥E 3BD =2CD =DE17．（18-19七年级下·黑龙江·期末）如图，为的中线，点在的延长线上，连接，CD ABC E DC BE 且，过点作于点，连接，若，，则的长为 ．BE AC =B BH CD ⊥H AH CE BH =18ABH S = DH18．（七年级下·山西临汾·期末）如图，在中，，垂足为D ，E 为外一点，连接ABC BD AC ⊥ABC ，且，．若，则的长为 ．BE CE ，AB BE =180BAD BEC ∠+∠=︒4,3CD CE ==AC三、解答题（本大题共6小题，共58分）19．（8分）（八年级上·浙江温州·期中）已知，如图，在中，是的中点，于点，ABC D BC DE AB ⊥E 于点，且．求证：．完成下面的证明过程．DF AC ⊥F BE CF =B C ∠=∠证明：，，DE AB ∵∵DF AC ⊥__________．BED ∴∠=90=︒是的中点，D BC __________，BD ∴=又，BE CF = __________．Rt RtBDE CDF ∴△≌△．B C ∴∠=∠20．（8分）（八年级上·内蒙古巴彦淖尔·阶段练习）如图，相交于点O ，，AD BC ，AD BC =．90C D ∠=∠=︒（1）求证：；ACB BDA △≌△（2）若，求的度数．28ABC ∠=︒CAO ∠21．（10分）（八年级下·陕西咸阳·阶段练习）如图，已知，，点在边的延长ABC 108ACB ∠=︒D BC 线上，连接，的平分线交于点，过点作，垂足为，且．AD ABC ∠AD E E EH BD ⊥H 54CEH ∠=︒（1）求的度数；ACE ∠（2）请判断是否平分，并说明理由．AE CAF ∠22．（10分）（八年级上·河北邢台·阶段练习）如图，在中，，在的上方作ABC 90CAB ∠=︒BC ，使，且，与交于点，连接．BDC BD CD ==90BDC ∠︒AC BD E AD （1）若平分，求证：．CA BCD ∠2CE AB =（2）求的度数．DAC ∠23．（10分）（21-22八年级上·山东聊城·期末）如图，在△ABC 中∠ABC =45°，AD ⊥BC 于点D ，点E 为AD 上的一点，且BE =AC ，延长BE 交AC 于点F ，连接FD ．（1）求证：△BED ≌△ACD ；（2）若FC =c ，FB =b ，求的值．(用含a ，b 的式子表示)FCDFBD S S ∆∆24．（12分）（20-21七年级下·辽宁朝阳·期末）已知：两个等腰直角三角板△ACB 和△DCE （AC ＝BC ，DC ＝CE ，∠ACB ＝∠DCE ＝90°）如图所示摆放，连接AE 、BD 交于点O ．AE 与DC 交于点M ，BD 与AC 交于点N ．（1）如图1（两个等腰直角三角板大小不等），试判断AE 与BD 有何关系并说明理由；（2）如图2（两个等腰直角三角板大小相等，即AC ＝DC ），在不添加任何辅助线的情况，请直接写出图2中四对全等的直角三角形．参考答案：1．D【分析】本题考查了直角三角形全等的判定定理的应用，根据垂直定义得出，根据90BAC DCA ∠=∠=︒图形可知是公共直角边，根据直角三角形全等的判定得出需要添加的条件是斜边相等，能熟记全AC HL 等三角形的判定定理是解题的关键．【详解】解：∵，，AB AC ⊥CD AC ⊥∴，90BAC DCA ∠=∠=︒在和中，Rt ABC △Rt CDA △，AC CA AD CB =⎧⎨=⎩∴，()Rt Rt HL ABC CDA ≌故选：．D 2．D【分析】本题考查了全等三角形的判定与性质，熟练掌握“”是解答本题的关键．根据“”所需HL HL 的条件分析即可．【详解】解：∵，AC BD ⊥∴，90APB CPD ∠=∠=︒∵，AP CP =∴要利用“”判定的条件是．HL ABP CDP △≌△AB CD =故选D ．3．B【分析】本题考查全等三角形的判定和性质、解题的关键是熟练掌握全等三角形的判定和性质，属于基础题．首先证明，推出，，由，推出ABC CDE △△≌,CE AC D B =∠=∠CAB ECD =∠∠90D DCE ∠+∠=︒，推出，即可一一判断．B ∠+90DCE ∠=︒CD AB ⊥【详解】解：在和中，Rt ABC Rt CDE AB CD BC DE=⎧⎨=⎩,ABC CDE ∴ ≌，,,CE AC D B ∴=∠=∠CAB ECD =∠∠90,D DCE ∠+∠=︒ 90,B DCE ∴∠+∠=︒,CD AB ∴⊥故A 、C 、D 正确，故选：B ．4．B【分析】本题主要考查了全等三角形的性质与判定，三角形内角和定理，利用证明HL 得到，由可得．Rt Rt ABC ADEF △≌△2314∠=∠∠=∠，3490∠+∠=°90∠+∠=︒ABC DFE 【详解】解：由题意得，，90BAC EDF ∠=∠=︒∵，BC EF AC DF ==，∴，()Rt Rt HL ABC ADEF △≌△∴，2314∠=∠∠=∠，∵，3490∠+∠=°∴，即．2490∠+∠=︒90∠+∠=︒ABC DFE 故选：B．5．B【分析】先根据证明，再根据全等三角形的性质得出，最HL Rt Rt ABC DEF △≌△32CBA DEF ∠=∠=︒后根据直角三角形两锐角互余即可求解．【详解】解：在和中，Rt ABC △Rt DEF △，BC EF AC DF =⎧⎨=⎩∴，()Rt Rt HL ABC DEF ≌△△∴，32CBA DEF ∠=∠=︒∴，9058EFD DEF ∠=︒-∠=︒故选：B ．【点拨】本题主要考查了用证明三角形全等，解题的关键掌握有一条直角和斜边相等的两个直角三角HL 形全等．6．D【分析】证明Rt △FDC ≌Rt △DEB （HL ），由全等三角形的性质得出∠DFC ＝∠EDB ＝25°，即可得出答案．【详解】解：∵∠AFD ＝155°，∴∠DFC ＝25°，∵DF ⊥BC ，DE ⊥AB ，∴∠FDC ＝∠DEB ＝90°，在Rt △FDC 和Rt △DEB 中，，CF BD CD BE =⎧⎨=⎩∴Rt △FDC ≌Rt △DEB （HL ），∴∠DFC ＝∠EDB ＝25°，∴∠EDF ＝180°−∠BDE −∠FDC ＝180°−25°−90°＝65°．故选：D ．【点拨】本题考查了全等三角形的判定与性质，熟练掌握全等三角形的判定定理和性质定理是解题的关键．7．A【分析】本题考查全等三角形的判定与性质，根据题意，利用直角三角形全等的判定定理得到，求出相关线段长度，由图中线段关系表示出，代值求()Rt Rt HL EDC BAC ≌EA EC AC BC AC =-=-解即可得到答案，熟练掌握两个三角形全等的判定与性质是解决问题的关键．【详解】解：，3.5AC = ，∴ 3.5CD AC ==，EC BD ⊥，ECD BCA ∴∠=∠在和中，Rt EDC Rt BAC AC CD AB ED=⎧⎨=⎩，∴()Rt Rt HL EDC BAC ≌，EC BC ∴=，9 3.5 5.5BC BD CD BD AC =-=-=-= ，5.5 3.52EA EC AC BC AC ∴=-=-=-=故选：A ．8．B【分析】本题主要考查全等三角形的判定与性质，直角三角形中两个锐角互余，根据条件证明出两个直角三角形全等是解题的关键．【详解】解：，，CD AD ⊥ CB AB ⊥，90ADC ABC ∴∠=∠=︒在和中，Rt ADC Rt ABC ，CD CB AC AC =⎧⎨=⎩，()Rt ADC Rt ABC HL ∴ ≌，ACD ACB ∴∠=∠，100BCD ∠=︒ ，111005022ACB BCD ∴∠=∠=⨯︒=︒．90905040BAC ACB ∴∠=︒-∠=︒-︒=︒故选：B ．9．A【分析】先根据角平分线的性质得到ED ＝EC ，再证明Rt △BED ≌Rt △BEC 得到DE ＝CE ，接着利用三角形周长和等线段代换得到AD ＋AC ＋2BC ＝12和AD ＋AC ＝6，所以6＋2BC ＝12，从而得到BC 的长．【详解】解：连接BE，∵DE ⊥AB∴∠BDE =90°，在Rt △BED 和Rt △BEC 中，，BE BE BD BC =⎧⎨=⎩∴Rt △BED ≌Rt △BEC （HL ），∴DE ＝CE ，∵△ABC 的周长为12，∴AB ＋AC ＋BC ＝12，即AD ＋AC ＋2BC ＝12，∵△ADE 的周长为6，∴AD ＋DE ＋AE ＝6，即AD ＋EC ＋AE ＝6，∴AD ＋AC ＝6，∴6＋2BC ＝12，∴BC ＝3．故选：A ．【点拨】本题考查了全等三角形的判定和性质，掌握HL 证明全等是解答此题的关键．10．D【分析】本题主要考查了直角三角形全等的判定方法，判定两个直角三角形全等的一般方法有：．熟练掌握运用全等三角形的判定方法是解题关键．SSS SAS ASA AAS HL 、、、、，，利用全等ADO AEO ≌,,,,DOC EOB COM BOM ACM ABM ADB AEC BCE CBD ≌≌≌≌≌三角形的判定可证明，做题时，要结合已知条件与三角形全等的判定方法逐个验证．【详解】解：，ADO AEO ≌．理由如下：,,,,DOC EOB COM BOM ACM ABM ADB AEC BCE CBD ≌≌≌≌≌在与中，，ADO AEO 90ADO AEO ∠∠==︒，OA OA OD OE =⎧⎨=⎩∴，()ADO AEO HL ≌∴，,DAO EAO AD AE ∠∠==在与中，DOC EOB90ODC OEB OD OE DOC EOB ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴，()DOC EOB ASA ≌∴，,DC EB OC OB ==∴，即，DC AD EB AE +=+AC AB =∵，DAO EAO ∠∠=∴．AM BC CM BM ⊥=，在与中，，COM BOM 90OMC OMB ∠∠==︒，OC OB OM OM =⎧⎨=⎩∴．()COM BOM HL ≌在与中，，ACM ABM 90AMC AMB ∠∠==︒，AC AB AM AM =⎧⎨=⎩∴．()ACM ABM HL ≌在与中，ADB AEC ，AD AE DAB EACAB AC =⎧⎪∠=∠⎨⎪=⎩∴．()ADB AEC SAS ≌在与中，，BCE CBD 90BEC CDB ∠∠==︒BC CB BE CD=⎧⎨=⎩∴．()BCE CBD HL ≌故选：D11．/度30︒30【分析】本题考查了全等三角形的判定与性质，证即可求解．AEB BDA ≌△△【详解】解：∵分别是边上的高，AD BE 、BC AC 、∴90AEB BDA ∠=∠=︒∵，60CAB ∠=︒∴30EBA ∠=︒∵，AE BD =AB BA=∴()Rt AEB Rt BDA HL ≌∴，60DBA EAB ∠=∠=︒∴30CBE DBA EBA ∠=∠-∠=︒故答案为：30︒12．3【分析】本题主要考查了全等三角形的性质与判定，如图所示，连接，利用证明BE HL 得到，根据三角形周长公式推出，再由Rt Rt EBC EBD △≌△CE DE =6cm AD AC +=，可得．12cm BC BD AD AC +++=3cm BC =【详解】解：如图所示，连接，BE ∵，，DE AB ⊥90C ∠=︒∴，90C BDE ∠=∠=︒在和中，Rt EBC Rt EBD △，BC BD BE BE =⎧⎨=⎩∴，()Rt Rt HL EBC EBD △≌△∴，CE DE =∵的周长为，的周长为，ABC 12cm ADE 6cm ∴，12cm 6cm AB AC BC AD DE AE ++=++=，∴，即，6cm AD AE CE ++=6cm AD AC +=∵，12cm BC BD AD AC +++=∴，26cm 12cm BC +=∴，3cm BC =故答案为：3．13．90∠+∠=︒ABC DFE 【分析】由条件信息可得，与均是直角三角形，由已知可根据判定两三角形全等，再根ABC DEF HL 据全等三角形的对应角相等，不难求解．【详解】解：，证明如下：90∠+∠=︒ABC DFE 由题意可得：与均是直角三角形，且．ABC DEF BC EF AC DF ==，在和中，Rt ABC △Rt DEF △ ，BC EF AC DF =⎧⎨=⎩∴，()Rt Rt HL ABC DEF ≌ ∴，ABC DEF ∠=∠∵，90DEF DFE ∠+∠=︒∴．90∠+∠=︒ABC DFE 故答案为：90∠+∠=︒ABC DFE 【点拨】此题考查了全等三角形的应用．做题时要注意找已知条件，根据已知选择方法得出全等三角形是解题关键．14．①②④【分析】本题考查了全等三角形的判定与性质．利用证明全等，根据全等三角形HL Rt Rt BED CFD △≌△对应边相等可得，再证明，判断出平分，可得，DE DF =()Rt Rt HL AED AFD ≌△△AD BAC ∠AE AF =再根据图形即可得到．2AC AB BE -=【详解】解：∵，DE AB ⊥DF AC⊥∴，90E DFC ∠=∠=︒又∵，，BD CD =BE CF =∴，()Rt Rt HL BED CFD ≌∴，①正确，符合题意；DE DF =又∵，，90E DFC ∠=∠=︒AD AD =∴，()Rt Rt HL AED AFD ≌△△∴，，即平分，②正确，符合题意；AE AF =∠∠E A D FA D =AD BAC ∠∴，④正确，符合题意；2AC AB BE CF BE -=+=在中，，∴，③错误，不符合题意；Rt ADE △90E ∠=︒AD AE >综上所述，正确的是①②④．故答案为：①②④．15．35︒【分析】过点E 作，垂足为F ．由三角形的内角和定理求得，由角平分线的定义可EF AD ⊥55CDE ∠=︒知，由平行线的判定定理可知，由平行线的性质可求得，由角平分线110CDA ∠=︒AB CD ∥70DAB ∠=︒的性质可知，则，根据可证明，从而得到EF EC =EF BE =HL Rt Rt AEF AEB ≌ ．1352EAB DAB ∠=∠=︒【详解】解：过点E 作，垂足为F ．EF AD ⊥∵，9035C CED ∠=︒∠=︒，∴．55CDE ∠=︒∵平分，DE ADC ∠∴．55EDF ∠=︒∴．110CDA ∠=︒∵，90B C ∠=∠=︒∴．AB CD ∥∴．180CDA DAB ∠+∠=︒∴．70DAB ∠=︒∵平分，，DE CDA ∠EF AD EC DC ⊥⊥，∴．EF EC =∵E 是的中点，BC∴．EF BE =在和中，Rt AEF Rt AEB ，EF BE AE AE =⎧⎨=⎩∴．Rt Rt AEF AEB ≌ ∴．EAF EAB ∠=∠∴．11703522EAB DAB ∠=∠=⨯︒=︒故选答案为．35︒【点拨】本题主要考查的是角平分线的性质、全等三角形的性质和判定、平行线的性质和判定、三角形的内角和定理等知识点，由角平分线的性质证得是解题的关键．EF EC =16．12【分析】过点A 作交的延长线于点F ，根据证明，得到，AF CD ⊥CD AAS AFC AEB ≌△△AF AE =，再根据证明，得到，最后根据线段的和差即可求解．CF BE =HL Rt Rt AFD AED ≌ DF DE =【详解】解：过点A 作交的延长线于点F ，AF CD ⊥CD，90AFC ∴∠=︒，AE BD ⊥ ，90AFC AED AEB ∴∠=∠=∠=︒在和中，AFC △AEB ∵，90AFC AEB ABE ACDAC AB ∠=∠=︒⎧⎪∠=∠⎨⎪=⎩，()AAS AFC AEB ∴≌ ∴，，AF AE =CF BE =在和中，Rt AFD △Rt AED △，AF AE AD AD =⎧⎨=⎩，()Rt Rt HL AFD AED ∴≌ ，DF DE ∴=，，，CF CD DF =+ BE BD DE =-CF BE =，CD DF BD DE ∴+=-，2DE BD CD ∴=-，，3BD = 2CD =，21DE ∴=，12DE ∴=故答案为：．12【点拨】此题主要考查了全等三角形的判定与性质，正确作出辅助线构造全等三角形是解答此题的关键．17．3【分析】过点作于点，证明，，得出，A AF EF ⊥F ()AAS ADF BDH ≌Rt Rt (HL)CAF EBH ≌2BH HD DF DH =+=再由为的中线及，根据的面积列出关于的方程，求解即可．CD ABC BH CD ⊥BHD S HD 【详解】解：如图，过点作于点A AFEF ⊥F为的中线，CD ABC BH CD⊥，AD BD ∴=90AFD BHD ∠=∠=︒又ADF BDH∠=∠()AAS ADF BDH ∴ ≌，AF BH ∴=FD HD=在和中Rt CAF △Rt EBH △AF BH AC BE=⎧⎨=⎩Rt Rt (HL)CAF EBH ∴ ≌EH CF∴=，即EH CH CF CH ∴-=-EC HF=，，BH EC = EC HF HD DF ==+HD DF=2BH HD DF DH∴=+=为的中线，CD ABC BH CD ⊥1118922BHD ABH S S ∴==⨯= 又11222BHD S HD HB HD HD ==⨯ ∴1292HD HD ⨯=解得：3HD =故答案为：3．【点拨】本题考查了全等三角形的判定与性质、等底同高三角形的面积关系及直角三角形的面积公式，属于中档题．18．5【分析】如图，过作的延长线于，证明，则，，证B BF CE ⊥F ()AAS ABD EBF ≌AD EF =BD BF =明，则，，，根据，计算求()Rt Rt HL BCD BCF ≌4CF CD ==1EF CF CE =-=1AD =AC AD CD =+解即可．【详解】解：如图，过作的延长线于，B BF CE ⊥F∵，，180BAD BEC ∠+∠=︒180BEF BEC ∠+∠=︒∴，BAD BEF ∠=∠∵，，，BAD BEF ∠=∠90ADB EFB ∠=∠=︒AB BE =∴，()AAS ABD EBF ≌∴，，AD EF =BD BF =∵，，BD BF =BC BC =∴，()Rt Rt HL BCD BCF ≌∴，4CF CD ==∴，，1EF CF CE =-=1AD =∴，5AC AD CD =+=故答案为：5．【点拨】本题考查了全等三角形的判定与性质．解题的关键在于明确线段之间的数量关系．19．，，CFD ∠CD ()HL 【分析】本题考查了全等三角形的判定与性质知识；证明，得出即()Rt Rt HL BDE CDF △≌△B C ∠=∠可．证明三角形全等是解题的关键．【详解】解：，，DE AB ∵∵DF AC ⊥90BED CFD ∴∠=∠=︒是的中点，D BC BD CD∴=又，BE CF = ()Rt Rt HL BDE CDF ∴ ≌．B C ∴∠=∠20．(1)见详解(2)34CAO ∠=︒【分析】（1）由“”可证；HL Rt ACB Rt BDA ≌（2）由全等三角形的性质可得，即可求解．BAD ABC ∠=∠=28︒【详解】（1）证明：∵，90C D ∠=∠=︒∴和都是直角三角形，ACB △BDA △在和中，Rt ACB Rt BDA ，,AD BC AB BA ==AD BC AB BA=⎧⎨=⎩∴；()Rt ACB Rt BDA HL ≌（2）在中，Rt ACB ∵，28ABC ∠=︒902862,CAB ∴∠=︒-︒=︒由（1）可知，ACB BDA △≌△28,BAD ABC ∴∠=∠=︒622834.CAO CAB BAD ∴∠=∠-∠=︒-︒=︒【点拨】本题考查了全等三角形的判定和性质，证明是本题的关键．ACB BDA △≌△21．(1)36ACE ∠=︒(2)平分，理由见解析AE CAF ∠【分析】（1）由平角的定义可求解的度数，再利用三角形的内角和定理可求解，进ACD ∠36ECH ∠=︒而可求解；（2）过点分别作于点，于点，根据角平分线的性质可证得E EM BF ⊥M EN AC ⊥N ，进而可证明结论．EM EN =【详解】（1），108ACB ∠=︒ ．18010872ACD ∴∠=︒-︒=︒，EH BD ⊥ ．90CHE ∴∠=︒，54CEH ∠=︒，905436ECH ∴∠=︒-︒=︒；723636ACE ∴∠=︒-︒=︒（2）平分AE CAF∠理由：如图，过点分别作于点，于点E EM BF ⊥M EN AC ⊥N平分BE ABC∠FBE DBE∴∠=∠,,EM BF EH BD EN AC⊥⊥⊥ 90CHE ENA EMB ∴∠=∠=∠=︒在和中EMB EHB 90CHE EMB BE EBFBE DBE ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩（AAS ）EMB EHB ∴ ≌EM EH∴=36ACE ECH ∠=∠=︒同理可得：∴EN EH=EM EN∴=在和中，NAE MAE 90EM EN EMA ENA AE EA =⎧⎪∠=∠=︒⎨⎪=⎩（HL ）NAE MAE ∴ ≌AEN AEM∴∠=∠平分．AE ∴CAF∠【点拨】本题主要考查角平分线的判定与性质，三角形的内角和定理，掌握角平分线的判定与性质是解题的关键．22．(1)见解析(2)45︒【分析】本题主要考查全等三角形的判定和性质即角平分线性质，（1）延长，交于点，由题意得，有，由垂直得，证得BA CD F CAB CAF ≌AB AF =DBF DCE ∠=∠，有即可证明结论；BDF CDE ≌BF CE =（2）过点分别作于点，于点，有，得到，可得D DN BF ⊥N DM AC ⊥M DBNDCM △≌△DN DM =，即可求得角度．≌D A N D A M 【详解】（1）证明：延长，交于点，如图，BA CD F，，，BCA FCA ∠=∠ CA CA =90CAB CAF ∠=∠=︒，()ASA CAB CAF ∴ ≌，AB AF ∴=．2BF AB ∴=，，90DBF F ∠+∠=︒ 90DCE F ∠+∠=︒．DBF DCE ∴∠=∠，，90BDF CDE ∠=∠=︒ BD CD =，()ASA BDF CDE ∴ ≌，BF CE ∴=．2CE AB ∴=（2）解：过点分别作于点，于点，如图，D DN BF ⊥N DM AC ⊥M．90DNB DMC ∴∠=∠=︒，，DBN DCM ∠=∠ BD CD =，()AAS DBN DCM ∴ ≌，DN DM ∴=∵，DA DA =∴，()HL DAN DAM ≌．1452DAC DAF FAC ∴∠=∠=∠=︒23．(1)见解析(2)FCD FBD S c S b∆∆=【分析】（1）利用得，又BE =AC ，，因此可以通过HL45BAD ABC ==︒∠∠BD AD =90ADB ADC ∠=∠=︒定理证明；Rt Rt BED ACD ∆≅∆（2）作于点，作于点，由可得，利用DG BE ⊥G DH AC ⊥H BED ACD S S ∆∆=DG DH =即可求解．1212FCDFBD FC DH S S FB DG ∆∆⋅=⋅【详解】（1）证明：在△ABC 中∠ABC =45°，AD ⊥BC ，，，90ADB ADC ∴∠=∠=︒45BAD ABC ==︒∠∠，BD AD ∴=在和中，Rt BED ∆Rt ACD ∆，BD AD BE AC =⎧⎨=⎩，Rt ΔRt Δ()BED ACD HL ∴≅即．BED ACD ∆≅∆（2）解：如图所示，作DG ⊥BE 于点G ，作DH ⊥AC 于点H，由（1）知BED ACD∆≅∆，BED ACD S S ∆∆∴=，1122BE DG AC DH ∴⋅=⋅，BE AC = ，DG DH ∴=．1212FCDFBD FC DH S FC c S FB b FB DG ∆∆⋅∴===⋅【点拨】本题考查全等三角形的判定和性质，以及三角形的面积公式，解题的关键是正确作出辅助线，由可得．BED ACD S S ∆∆=DG DH =24．（1）AE ＝BD 且AE ⊥BD ．理由见解析；（2）△ACB ≌△DCE ，△EMC ≌△BCN ，△AON ≌△DOM ，△AOB ≌△DOE【分析】（1）证明△ACE ≌△BCD ，可得AE ＝BD ，∠CEA ＝∠BDC ，由∠CME ＝∠DMO ，根据三角形内角和定理即可得∠DOM ＝∠ECM ＝90°，进而可证AE ⊥BD ．（2）根据三角形全等的判定找出相等边和角，进而找出全等三角形．【详解】解：（1）结论；AE ＝BD 且AE ⊥BD ．理由如下：∵∠ACB ＝∠DCE ，∴∠ACB +∠DCA ＝∠DCE +∠DCA ，即∠DCB ＝∠ACE ，∵AC ＝BC ，CD ＝CE ，在△ACE 与△BCD 中，，AC BC ACE DCBCD CE =⎧⎪∠=∠⎨⎪=⎩∴△ACE ≌△BCD （SAS ），∴AE ＝BD ，∠CEA ＝∠BDC ，∵∠CME ＝∠DMO ，，∴180()180()CEA CME DMO BDC ︒-∠+∠=︒-∠+∠即∠DOM ＝∠ECM ＝90°，∴AE ⊥BD ，∴AE ＝BD 且AE ⊥BD ；（2）∵AC ＝DC ，∴AC ＝CD ＝EC ＝CB ，在△ACB 与△DCE 中，，AC DC ACB DCECB CE =⎧⎪∠=∠⎨⎪=⎩∴△ACB ≌△DCE （SAS ）；由（1）可知：∠AEC ＝∠BDC ，∠EAC ＝∠DBC ，∴∠DOM ＝90°，∵∠AEC ＝∠CAE ＝∠CBD ，∴△EMC ≌△BCN （ASA ），∴CM ＝CN ，∴DM ＝AN ，∴△AON ≌△DOM （AAS ），∵DE ＝AB ，AO ＝DO ，∴△AOB ≌△DOE （HL ）．【点拨】本题考查了三角形全等的性质与判定，掌握三角形全等的性质与判定是解题的关键．。

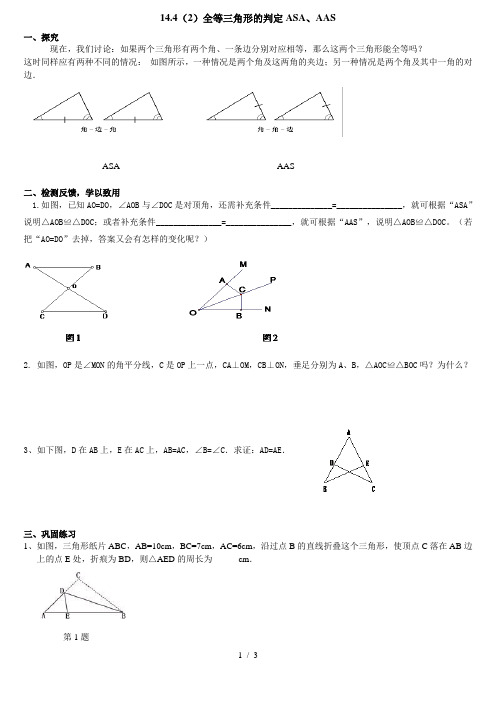
14.4（2）全等三角形的判定ASA、AAS一、探究现在，我们讨论：如果两个三角形有两个角、一条边分别对应相等，那么这两个三角形能全等吗？这时同样应有两种不同的情况：如图所示，一种情况是两个角及这两角的夹边；另一种情况是两个角及其中一角的对边．ASA AAS二、检测反馈，学以致用1.如图，已知AO=DO，∠AOB与∠DOC是对顶角，还需补充条件______________=_______________，就可根据“ASA”说明△AOB≌△DOC；或者补充条件_______________=_______________，就可根据“AAS”，说明△AOB≌△DOC。

（若把“AO=DO”去掉，答案又会有怎样的变化呢？）2. 如图，OP是∠MON的角平分线，C是OP上一点，CA⊥OM，CB⊥ON，垂足分别为A、B，△AOC≌△BOC吗？为什么？3、如下图，D在AB上，E在AC上，AB=AC，∠B=∠C．求证：AD=AE．三、巩固练习1、如图，三角形纸片ABC，AB=10cm，BC=7cm，AC=6cm，沿过点B的直线折叠这个三角形，使顶点C落在AB边上的点E处，折痕为BD，则△AED的周长为______cm．第1题2、已知：如图 , ∠1=∠2 , ∠3=∠4求证：AC=AB．3．如图，AB⊥BC，AD⊥DC，∠BAC=∠CAD.试说明：AB=AD .4、已知：如图 , FB=CE , AB∥ED , AC∥FD.F、C在直线 BE上．求证：AB=DE , AC=DF．5、如图，在△ABC中，∠C=2∠B,AD是△ABC的角平分线，∠1=∠B,试说明：AB=AC+AD6、已知：如图，AB=DC，∠A=∠D．试说明：∠1=∠2．7.如图，ΔABC中，D是AC上一点，BE∥AC，BE=AD，AE分别交BD、BC于点F、G．⑴图中有全等三角形吗？请找出来，并证明你的结论．⑵若连结DE，则DE与AB有什么关系？并说明理由．。

2022-2023学年八年级数学上册章节同步实验班培优题型变式训练（人教版）12.2 三角形全等的判定【题型1】SSS 证明三角形全等1．（2022·山西·运城市盐湖区教育科技局教学研究室七年级期末）小华在复习用尺规作一个角等于已知角的过程中，回顾了作图的过程，他发现OCD V 与'''O C D V 全等，请你说明小华得到全等的依据是（ ）A ．SSSB ．SASC ．ASAD ．AAS【答案】A 【分析】利用全等三角形的判定定理即可求解．【详解】解：在OCD D 和O C D ¢¢¢D 中，OD O D OC O C DC D C ¢¢¢¢¢=ì¢ï=íï=î，()OCD O C D SSS ¢¢¢\D @D ．故选：A ．【点睛】本题主要考查全等三角形的判定，掌握全等三角形的判定定理是解题的关键．【变式1-1】2．（2021·重庆·华东师范大学附属中旭科创学校八年级期中）已知，如图，AD=AC ，BD=BC ，O 为AB 上一点，那么图中共有___对全等三角形．【答案】3【分析】由已知条件，结合图形可得△ADB ≌△ACB ，△ACO ≌△ADO ，△CBO ≌△DBO 共3对．找寻时要由易到难，逐个验证．【详解】解：∵AD=AC ，BD=BC ，AB=AB，∴△ADB ≌△ACB ；∴∠CAO=∠DAO ，∠CBO=∠DBO ，∵AD=AC ，BD=BC ，OA=OA ，OB=OB∴△ACO ≌△ADO ，△CBO ≌△DBO ．∴图中共有3对全等三角形．故答案为3．【题型2】SAS 证明三角形全等1．（2022·全国·八年级专题练习）如图，已知∠1＝∠2，∠3＝∠4，要证BC ＝CD ，证明中判定两个三角形全等的依据是（ ）A ．角角角B ．角边角C ．边角边D ．角角边【答案】B 【分析】根据已知条件，直接利用ASA 进行证明即可求解．【详解】解：在△ABC 与△ADC 中，1234AC AC Ð=Ðìï=íïÐ=Ðî，则△ABC ≌△ADC （ASA ）．∴BC ＝CD ．故选：B ．【点睛】本题考查了全等三角形的判定，掌握全等三角形的判定方法是解题的关键．【变式2-1】2．（2022·全国·八年级课时练习）如图，BE BA =，//AB DE ，BC DE =，若40BAC Ð=°，25E Ð=°，则BDE Ð=___．【答案】115°【分析】根据//AB DE ，推出Ð=ÐABC BED ，联合题目的条件可证明(SAS)BED ABC ≌△△，进而可求得结论．【详解】解：∵//AB DE ，∴Ð=ÐABC BED ，在BED V 与ABC V 中BE AB BED ABC DE CB =ìïÐ=Ðíï=î，∴(SAS)BED ABC ≌△△，∴40EBD BAC Ð=Ð=°，而180BDE EBD E Ð=°-Ð-Ð，且25E Ð=°，∴1804025115BDE Ð=°-°-°=°，故答案为：115°．【点睛】本题考查利用SAS 判定三角形全等，三角形内角和定理，利用平行推出角等，进而推出三角形全等是解题关键．【题型3】ASA 或AAS 证明三角形全等1．（2022·河北·平乡县第二中学八年级阶段练习）已知如图，要测量水池的宽AB ，可过点A 作直线AC ⊥AB ，再由点C 观测，在BA 延长线上找一点B ¢，使ACB ACB ¢ÐÐ＝，这时只要出AB ¢的长，就知道AB 的长，那么判定ABC D ≌AB C D ¢的理由是（ ）A ．ASAB ．AASC ．SASD ．HL【答案】A 【分析】直接利用全等三角形的判定方法得出答案．【详解】解：∵AC ⊥AB ，∴90CAB CAB Ð=Т=°，在ABC D 和AB C D ¢中，ACB ACB AC ACCAB CAB Ð=Ðìï=íïТ=Ðî¢，∴ABC D ≌()ASA AB C D ¢，∴AB AB ¢=．故选A ．【点睛】本题考查了全等三角形的应用，解题的关键是能够利用ASA 判定两个三角形全等．【变式3-1】2．（2021·江苏南京·八年级阶段练习）如图，AB 、CD 相交于点E ，且AE ＝BE ，AC BD ∥．求证：△AEC ≌△BED ．【答案】见解析【分析】采用“ASA ”的全等三角形的判定方法即可求证．【详解】∵AC BD∥∴∠A ＝∠B ，在△AEC 和△BED 中，A B AE BEAEC BED Ð=Ðìï=íïÐ=Ðî，∴△AEC ≌△BED （ASA ），【点睛】本题考查了全等三角形的判定以及平行线的性质的知识，掌握全等三角形的判定方法是解答本题的关键．【题型4】HL 证明三角形全等1．（2022·全国·八年级专题练习）如图，已知AD BD ^，BC AC ^，AC BD =．则CAB DBA △△≌的理由是（ ）A ．HLB ．SASC ．AASD ．ASA 【答案】A 【分析】利用直角三角形全等的判定方法进行判断．【详解】证明：∵AD ⊥BD ，BC ⊥AC ，∴∠C ＝∠D ＝90°，在Rt △CAB 和Rt △DBA 中，AB BA AC BD =ìí=î，∴Rt △CAB ≌Rt △DBA （HL ）．故选：A ．【点睛】本题考查了全等三角形的判定，熟练掌握直角三角形全等的判定是解决问题的关键．【变式4-1】2．（2022·湖南·新化县东方文武学校八年级期中）如图，AB =AD ，CB ⊥AB 于点B ，CD ⊥AD 于点D ，求证△ABC ≌△ADC ．【答案】见解析【分析】求出∠B =∠D =90°，根据全等三角形的判定定理得出Rt △ABC ≌Rt △ADC ．【详解】解：∵CB ⊥AB ，CD ⊥AD∴∠B =∠D =90°又∵AB =AD ，AC =AC∴Rt △ABC ≌Rt △ADC （HL ）【点睛】本题考查了全等三角形的判定定理和性质定理，能灵活运用定理进行推理是解此题的关键．【题型5】全等三角形判定的灵活应用1．（2021·甘肃·庄浪县阳川中学八年级期中）下列各组条件中，可以判定△ABC ≌△DEF 的条件是（ ）A ．AB =DE 、AC =DF 、BC =EFB ．∠A =∠D 、∠B =∠E 、∠C =∠F C ．AB =DE 、AC =DF 、∠C =∠FD ．BC =EF 、∠A =∠D 【答案】A 【分析】全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，直角三角形全等还有HL ，根据以上定理判断即可【详解】解： A 、符合全等三角形的判定定理SSS ，即能推出△ABC ≌△DEF ，故本选项符合题意；B 、只有角相等，不能判定△ABC ≌△DFE ，故本选项不合题意；C 、只满足SSA ，不符合全等三角形的判定定理，即不能推出△ABC ≌△DEF ，故本选项不合题意；D 、只有一角一边两个条件，不符合全等三角形的判定定理，即不能推出△ABC ≌△DEF ，故本选项不合题意； 故选A ．【点睛】本题考查了全等三角形的判定定理的应用，能熟记全等三角形的判定定理是解此题的关键，注意：全等三角形的判定定理有SAS ，ASA ，AAS ，SSS ，直角三角形全等还有HL ．【变式5-1】2．（2022·浙江·舟山市普陀第二中学八年级期末）如图，在ABC V 中，AD 是BC 边上的高，BE 是AC 边上的高，且AD ，BE 交于点F ，若BF AC =，BD =8，3CD =，则线段AF 的长度为______．【答案】5【分析】首先证明△BDF ≌△ADC ，再根据全等三角形的性质可得FD =CD ，AD =BD ，根据AD =8，DF =3，即可算出AF 的长．【详解】解：∵AD 是BC 边上的高，BE 是AC 边上的高，∴∠ADC =∠FDB =90°，∠AEB =90°，∴∠1+∠C =90°，∠1+∠2=90°，∴∠2=∠C ，∵∠2=∠3，∴∠3=∠C ，在△ADC 和△BDF 中，3C FDB CDA BF AC Ð=ÐìïÐ=Ðíï=î，∴△BDF ≌△ADC （AAS ），∴FD =CD ，AD =BD ，∵CD =3，BD =8，∴AD =8，DF =3，∴AF =8-3=5，故答案为：5．【点睛】本题考查的是全等三角形的判定及性质，熟练掌握性质定理是解题的关键．一．选择题1．（2022·福建·福州十八中八年级期末）如图，已知AC BD ^，垂足为O ，AO CO =，AB CD =，则可得到AOB COD D @D ，理由是( )A ．HLB ．SASC ．ASAD ．AAS【答案】A 【分析】根据全等三角形的判定定理分析即可．【详解】解:∵AC BD^∴∠AOB=∠COD=90°在Rt △AOB 和Rt △COD 中AO CO AB CD=ìí=î∴AOB COD D @D （HL ）故选A ．【点睛】此题考查的是全等三角形的判定定理，掌握用HL 判定两个三角形全等是解决此题的关键．2．（2022·全国·七年级期末）如图，为测量桃李湖两端AB 的距离，南开中学某地理课外实践小组在桃李湖旁的开阔地上选了一点C ，测得∠ACB 的度数，在AC 的另一侧测得∠ACD =∠ACB ，CD =CB ，再测得AD 的长，就是AB 的长．那么判定△ABC ≌△ADC 的理由是（ ）A ．SASB ．SSSC ．ASAD ．AAS【答案】A【分析】已知条件是∠ACD =∠ACB ，CD =CB ，AC =AC ，据此作出选择．【详解】解：在△ADC 与△ABC 中，CD CB ACD ACB AC AC =ìïÐ=Ðíï=î．∴△ADC ≌△ABC （SAS ）．故选：A ．【点睛】此题考查了全等三角形的应用，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS ，做题时注意选择．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．3．（2021·全国·七年级课时练习）如图，△ABC 和△EDF 中，∠B ＝∠D ＝90°，∠A ＝∠E ，点B ，F ，C ，D 在同一条直线上，再增加一个条件，不能判定△ABC ≌△EDF 的是( )A ．AB ＝EDB ．AC ＝EF C ．AC ∥EFD ．BF ＝DC 【答案】C【分析】根据全等三角形的判定方法即可判断.【详解】A. AB ＝ED ，可用ASA 判定△ABC ≌△EDF ；B. AC ＝EF ，可用AAS 判定△ABC ≌△EDF ；C. AC ∥EF ，不能用AAA 判定△ABC ≌△EDF ，故错误；D. BF ＝DC ，可用AAS 判定△ABC ≌△EDF ；故选C.【点睛】此题主要考查全等三角形的判定，解题的关键是熟知全等三角形的判定方法.4．（2022·全国·八年级课时练习）如图，在ABC V 中，D ，E 是BC 边上的两点，,,12110,60AD AE BE CD BAE ==Ð=ÐÐ=°=°，则BAC Ð的度数为（ ）A ．90°B ．80°C ．70°D ．60°【答案】B 【分析】先证明BD =CE ，然后证明△ADB ≌△AEC ，∠ADE =∠AED =70°，得到∠BAD =∠CAE ，根据三角形内角和定理求出∠DAE =40°，从而求出∠BAD 的度数即可得到答案．【详解】解：∵BE =CD ，∴BE -DE =CD -DE ，即BD =CE ，∵∠1=∠2=110°，AD =AE ，∴△ADB ≌△AEC （SAS ），∠ADE =∠AED =70°，∴∠BAD =∠CAE ，∠DAE =180°-∠ADE -∠AED =40°，∵∠BAE =60°，∴∠BAD =∠CAE =20°，∴∠BAC =80°，故选B ．【点睛】本题主要考查了全等三角形的性质与判定，邻补角互补，三角形内角和定理，熟知全等三角形的性质与判定条件是解题的关键．5．（2022·全国·八年级专题练习）如图，点B ，C ，E 在同一直线上，且AC CE =，90B D Ð=Ð=°，AC CD ^，下列结论不一定成立的是（ ）A ．2A Ð=ÐB ．90A E Ð+Ð=°C ．BC DE =D ．BCD ACEÐ=Ð【答案】D 【分析】根据直角三角形的性质得出∠A =∠2，∠1=∠E ，根据全等三角形的判定定理推出△ABC ≌△CDE ，再逐个判断即可．【详解】解：∵AC ⊥CD ，∴∠ACD =90°，∵∠B =90°，∴∠1+∠A =90°，∠1+∠2=90°，∴∠A =∠2，同理∠1=∠E ，∵∠D =90°，∴∠E+∠2=∠A+∠E=90°，在△ABC 和△CDE 中，2A B D AC CE Ð=ÐìïÐ=Ðíï=î，∴△ABC ≌△CDE （AAS ），∴BC DE =，∴选项A 、选项B ，选项C 都正确；根据已知条件推出∠A =∠2，∠E =∠1，但是∠1=∠2不能推出，而∠BCD =90°+∠1，∠ACE =90°+∠2，所以BCD ACE Ð=Ð不一定成立故选项D 错误；故选：D ．【点睛】本题考查了全等三角形的判定定理和直角三角形的性质，能灵活运用知识点进行推理是解此题的关键，注意：全等三角形的判定定理有：ASA ，SAS ，AAS ，SSS ，两直角三角形全等，还有HL ．6．（2022·江苏·八年级专题练习）如图，C 为线段AE 上一动点（不与点A ，E 重合），在AE 同侧分别作等边三角形ABC 和等边三角形CDE ，AD 与BE 交于点O ，AD 与BC 交于点P ，BE 与CD 交于点Q ，连结PQ ．以下结论错误的是（ ）A ．∠AOB =60°B ．AP =BQC ．PQ ∥AED ．DE =DP 【答案】D【分析】利用等边三角形的性质，BC ∥DE ，再根据平行线的性质得到∠CBE =∠DEO ，于是∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，得出A 正确；根据△CQB ≌△CPA （ASA ），得出B 正确；由△ACD ≌△BCE 得∠CBE =∠DAC ，加之∠ACB =∠DCE =60°，AC =BC ，得到△CQB ≌△CPA （ASA ），再根据∠PCQ =60°推出△PCQ 为等边三角形，又由∠PQC =∠DCE ，根据内错角相等，两直线平行，得出C 正确；根据∠CDE =60°，∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，可知∠DQE ≠∠CDE ，得出D 错误．【详解】解：∵等边△ABC 和等边△CDE ，∴AC =BC ，CD =CE ，∠ACB =∠DCE =60°，∴∠ACB +∠BCD =∠DCE +∠BCD ，即∠ACD =∠BCE ，在△ACD 与△BCE 中，AC BC ACD BCE CD CE =ìïÐ=Ðíï=î，∴△ACD ≌△BCE （SAS ），∴∠CBE =∠DAC ，又∵∠ACB =∠DCE =60°，∴∠BCD =60°，即∠ACP =∠BCQ ，又∵AC =BC ，在△CQB 与△CPA 中，ACP BCQ AC BCPAC CBQ Ð=Ðìï=íïÐ=Ðî，∴△CQB ≌△CPA （ASA ），∴CP =CQ ，又∵∠PCQ =60°可知△PCQ 为等边三角形，∴∠PQC =∠DCE =60°，∴PQ ∥AE ，故C 正确，∵△CQB ≌△CPA ，∴AP =BQ ，故B 正确，∵AD =BE ，AP =BQ ，∴AD -AP =BE -BQ ，即DP =QE ，∵∠DQE =∠ECQ +∠CEQ =60°+∠CEQ ，∠CDE =60°，∴∠DQE ≠∠CDE ，故D 错误；∵∠ACB =∠DCE =60°，∴∠BCD =60°，∵等边△DCE ，∠EDC =60°=∠BCD ，∴BC ∥DE ，∴∠CBE =∠DEO ，∴∠AOB =∠DAC +∠BEC =∠BEC +∠DEO =∠DEC =60°，故A 正确．故选：D ．【点睛】本题考查了等边三角形的性质、全等三角形的判定与性质，利用旋转不变性，解题的关键是找到不变量．二、填空题7．（2022·全国·八年级课时练习）如图，90B D Ð=Ð=°，AB AD =，130BAD Ð=°，则DCA Ð=______°．8．（2020·北京·中考真题）在V ABC 中，AB=AC ，点D 在BC 上（不与点B ，C 重合）．只需添加一个条件即可证明V ABD ≌V ACD ，这个条件可以是________（写出一个即可）【答案】∠BAD=∠CAD （或BD=CD ）【分析】证明V ABD ≌V ACD ，已经具备,,AB AC AD AD == 根据选择的判定三角形全等的判定方法可得答案．【详解】解：,,AB AC AD AD ==Q\ 要使,ABD ACD V V ≌则可以添加：∠BAD=∠CAD ，此时利用边角边判定：,ABD ACD V V ≌或可以添加：,BD CD =此时利用边边边判定：,ABD ACD V V ≌故答案为：∠BAD=∠CAD 或（.BD CD =）【点睛】本题考查的是三角形全等的判定，属开放性题，掌握三角形全等的判定是解题的关键．9．（2022·全国·八年级课时练习）如图，点D 、A 、E 在直线m 上，AB =AC ，BD ⊥m 于点D ，CE ⊥m 于点E ，且BD =AE ．若BD =3，CE =5，则DE =____________【答案】8【分析】根据BD ⊥m ，CE ⊥m ，得∠BDA =∠CEA =90°，再结合已知AB =AC ，BD =AE 可推出Rt △ADB ≌Rt △CEA ，最后由全等三角形的性质，即可计算出结果．【详解】解：∵BD ⊥m ，CE ⊥m ，∴∠BDA =∠CEA =90°，在Rt △ADB 和Rt △CEA 中，∵AB =AC ，BD =AE ，∴Rt △ADB ≌Rt △CEA （HL ），∵BD =3，CE =5，∴AE =BD =3，AD =CE =5，∴DE = AD + AE =8．故答案为：8．【点睛】本题考查了全等三角形的判定与性质，掌握利用HL 判定直角三角形的全等是解题的关键．10．（2022·全国·八年级专题练习）如图，在△ABC 中，∠ABC ＝90°，AB ＝CB ，F 为AB 延长线上一点，点E 在BC 上，且AE ＝CF ，若∠CAE ＝29°，则∠ACF 的度数为________°．【答案】61【分析】由“HL”可证Rt△ABE≌Rt△CBF，可得∠BAE＝∠BCF＝16°，即可求解．【详解】解：∵在△ABC中，∠ABC＝90°，AB＝CB，∴∠BAC＝∠BCA＝45°，∵∠CAE＝29°，∴∠BAE＝16°，在Rt△ABE和Rt△CBF中，AB BC AE CF=ìí=î，∴Rt△ABE≌Rt△CBF（HL），∴∠BAE＝∠BCF＝16°，∴∠ACF＝∠BCA＋∠BCF＝61°，故答案为：61．【点睛】本题考查了全等三角形的判定和性质，证明Rt△ABE≌Rt△CBF是本题的关键．11．（2021·广东·深圳市龙岗区木棉湾实验学校八年级阶段练习）如图，△ABC的面积为25cm2，BP平分∠ABC，过点A作AP⊥BP于点P，则△PBC的面积为________；∵BP 平分ABC Ð，∴ABP EBP Ð=Ð．∵AP BP ^，12．（2022·全国·八年级专题练习）如图，BD 是△ABC 的中线，E 为A B 边上一点，且:2:1AE EB =，连接CE 交BD 于F ，连接AF 并延长交BC 于点G ，则:BGF ADF S S =△△______．【答案】1:3【分析】作//DK EC ，交AB 于K ，作//DH BC ，交AG 于H ．通过平行线的性质证明AH GH =，GF FH =，3AH HF =，即可求出:1:3BGF ADF S S D D =．【详解】解：作//DK EC ，交AB 于K ，作//DH BC ，交AG 于H ，BD Q 是ABC D 的中线，AD CD \=，AK EK \=，AH GH =，:2:1AE EB =Q ，EB EK AK \==，//EF DK Q ，BF DF \=，//DH BC Q ，GBF HDF \Ð=Ð，在GBF D 和HDF D 中，GBF HDF BF DF BFG DFH Ð=Ðìï=íïÐ=Ðî，()GBF HDF ASA \D @D ，GF HF \=，BGF DHF S S D D =，AH GH =Q ，3AH HF \=，33ADF DHF BGF S S S D D D \==，:1:3BGF ADF S S D D \=，故答案为：1:3．【点睛】本题考查三角形的面积，三角形全等，平行线的性质，等高模型等知识，解题的关键是学会添加常用辅助线，构造平行线解决问题，属于中考常考题型．三、解答题13．（2022·江苏·八年级专题练习）如图，D 是AB 边上一点，DF 交AC 于点E ，DE ＝FE ，AE ＝CE ．求证：FC //AB ．【答案】见解析【分析】由DE =FE ，AE =CE ，易证得△ADE ≌△CFE ，即可得∠A =∠ECF ，则可证得FC ∥AB ．【详解】证明：在△ADE 和△CFE 中，DE FE AED CEF AE CE =ìïÐ=Ðíï=î，∴△ADE ≌△CFE （SAS ），∴∠A =∠ECF ，∴FC //AB ．【点睛】此题考查了全等三角形的判定与性质以及平行线的判定．此题难度不大，注意掌握数形结合思想的应用．14．（2022·江苏·八年级课时练习）已知：如图AD 为△ABC 的高，E 为AC 上一点BE 交AD 于F 且有BF ＝AC ，FD ＝CD ．求证：Rt △BFD ≌Rt △ACD ．【答案】证明见解析【分析】由题意可知BFD △和ACD △都为直角三角形，即可直接利用“HL ”证明BFD ACD @△△．【详解】证明：∵AD 是ABC V 的高，∴AD BC ^，即BFD △和ACD △都为直角三角形．∴在Rt BFD V 和Rt ACD △中BF AC FD CD =ìí=î，∴()BFD ACD HL @V V ．【点睛】本题考查全等三角形的判定；掌握判定三角形全等的方法是解答本题的关键．15．（2022·陕西·中考真题）如图，在△ABC 中，点D 在边BC 上，CD =AB ，DE ∥AB ，∠DCE =∠A ．求证：DE =BC ．【答案】证明见解析【分析】利用角边角证明△CDE ≌△ABC ，即可证明DE =BC ．【详解】证明：∵DE ∥AB ，∴∠EDC =∠B ．又∵CD =AB ，∠DCE =∠A ，∴△CDE ≌△ABC (ASA)．∴DE =BC ．【点睛】本题考查了全等三角形的判定和性质，掌握全等三角形的判定是本题的关键．16．（2021·广东广州·中考真题）如图，点E 、F 在线段BC 上，//AB CD ，A D Ð=Ð，BE CF =，证明：AE DF =．【答案】见解析【分析】利用AAS 证明△ABE ≌△DCF ，即可得到结论．【详解】证明：∵//AB CD ，∴∠B =∠C ，∵A D Ð=Ð，BE CF =，∴△ABE ≌△DCF （AAS ），∴AE DF =．【点睛】此题考查全等三角形的判定及性质，熟记全等三角形的判定定理是解题的关键．17．（2021·全国·八年级专题练习）如图，已知AB ＝DC ，AC ＝DB ，BE ＝CE,求证：AE ＝DE.【答案】见解析【分析】利用SSS 证明△ABC ≌△DCB ，根据全等三角形的性质可得∠ABC=∠DCB ，再由SAS 定理证明△ABE ≌△CED ，即可证得AE=DE ．【详解】证明：在△ABC 和△DCB 中，AB DC AC DB BC CB ìïíïî＝＝＝ ，∴△ABC ≌△DCB （SSS ）．∴∠ABC=∠DCB ．在△ABE 和△DCE 中，AB DCABC DCB BE CE ＝＝＝ìïÐÐíïî，∴△ABE ≌△DCE （SAS ）．∴AE=DE ．【点睛】本题考查三角形全等的判定方法，判定两个三角形全等的一般方法有：SSS 、SAS 、ASA 、AAS 、HL ．注意：AAA 、SSA 不能判定两个三角形全等，判定两个三角形全等时，必须有边的参与，若有两边一角对应相等时，角必须是两边的夹角．18．（2022·江苏泰州·九年级专题练习）如图，V ABC 中，AC ＝BC ，∠ACB ＝90°，AD 平分∠BAC 交BC 于点D ，过点B 作BE ⊥AD ，交AD 延长线于点E ，F 为AB 的中点，连接CF ，交AD 于点G ，连接BG ．（1）线段BE 与线段AD 有何数量关系？并说明理由；（2）判断V BEG的形状，并说明理由．。

全等三角形判定一（ASA ，SAS ）（提高）【学习目标】1．理解和掌握全等三角形判定方法1——“角边角”，和判定方法2——“边角边”；2．能把证明角相等或线段相等的问题，转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定1——“角边角”全等三角形判定1——“角边角”两角和它们的夹边对应相等的两个三角形全等（可以简写成“角边角”或“ASA ”）. 要点诠释：如图，如果∠A ＝∠'A ，AB ＝''A B ，∠B ＝∠'B ，则△ABC ≌△'''A B C .要点二、全等三角形判定2——“边角边”1. 全等三角形判定2——“边角边” 两边和它们的夹角对应相等的两个三角形全等（可以简写成“边角边”或“SAS ”）.要点诠释：如图，如果AB ＝ ''A B ，∠A ＝∠'A ，AC ＝ ''A C ，则△ABC ≌△'''A B C . 注意：这里的角，指的是两组对应边的夹角.2. 有两边和其中一边的对角对应相等，两个三角形不一定全等.如图，△ABC 与△ABD 中，AB ＝AB ，AC ＝AD ，∠B ＝∠B ，但△ABC 与△ABD 不完全重合，故不全等，也就是有两边和其中一边的对角对应相等，两个三角形不一定全等.【典型例题】类型一、全等三角形的判定1——“角边角”1、如图，G 是线段AB 上一点，AC 和DG 相交于点E.请先作出∠ABC 的平分线BF ，交AC 于点F ；然后证明：当AD∥BC，AD ＝BC ，∠ABC＝2∠ADG 时，DE ＝BF.【思路点拨】通过已知条件证明∠DAC＝∠C，∠CBF＝∠ADG，则可证△DAE≌△BCF【答案与解析】证明： ∵AD∥BC，∴∠DAC＝∠C∵BF 平分∠ABC∴∠ABC＝2∠CBF∵∠ABC＝2∠ADG∴∠CBF＝∠ADG在△DAE 与△BCF 中⎪⎩⎪⎨⎧∠=∠=∠=∠C DAC BCAD CBF ADG ∴△DAE≌△BCF（ASA ）∴DE＝BF【总结升华】利用全等三角形证明线段(角)相等的一般方法和步骤如下：(1)找到以待证角(线段)为内角(边)的两个三角形；(2)证明这两个三角形全等；(3)由全等三角形的性质得出所要证的角(线段)相等．举一反三：【变式】已知：如图，在△MPN 中，H 是高MQ 和NR 的交点，且MQ ＝NQ ．求证：HN ＝PM.【答案】证明：∵MQ 和NR 是△MPN 的高，∴∠MQN ＝∠MRN ＝90°，又∵∠1＋∠3＝∠2＋∠4＝90°，∠3＝∠4∴∠1＝∠2在△MPQ 和△NHQ 中，12MQ NQ MQP NQH ∠=∠⎧⎪=⎨⎪∠=∠⎩∴△MPQ ≌△NHQ （ASA ）∴PM ＝HN类型二、全等三角形的判定2——“边角边”2、如图，AD 是△ABC 的中线，求证：AB ＋AC ＞2AD ．【思路点拨】延长AD 到点E ，使AD ＝DE ，连接CE ．通过证全等将AB 转化到△CEA 中，同时也构造出了2AD ．利用三角形两边之和大于第三边解决问题.【答案与解析】证明：如图，延长AD 到点E ，使AD ＝DE ，连接CE ．在△ABD 和△ECD 中，AD ＝DE ，∠ADB ＝∠EDC ，BD ＝CD ．∴△ABD ≌△ECD ．∴AB ＝CE ．∵AC ＋CE ＞AE ，∴AC ＋AB ＞AE ＝2AD ．即AC ＋AB ＞2AD ．【总结升华】证明边的大小关系主要有两个思路：（1）两点之间线段最短；（2）三角形的两边之和大于第三边．要证明AB ＋AC ＞2AD ，如果归到一个三角形中，边的大小关系就是显然的，因此需要转移线段，构造全等三角形是转化线段的重要手段．可利用旋转变换，把△ABD 绕点D 逆时针旋转180°得到△CED ，也就把AB 转化到△CEA 中，同时也构造出了2AD ．若题目中有中线，倍长中线，利用旋转变换构造全等三角形是一种重要方法．3、（2020•吉林）如图，△ABC 和△DAE 中，∠BAC=∠DAE ，AB=AE ，AC=AD ，连接BD ，CE ，求证：△ABD ≌△AEC ．【思路点拨】根据∠BAC=∠DAE，可得∠BAD=∠CAE，再根据全等的条件可得出结论．【答案与解析】证明：∵∠BAC=∠DAE，∴∠BAC﹣∠BAE=∠DAE﹣∠BAE，即∠BAD=∠CAE，在△ABD和△AEC中，，∴△ABD≌△AEC（SAS）．【总结升华】本题考查利用“边角边”定理来证明三角形全等，注意等角减等角，差相等. 举一反三：【变式】（2020•启东市模拟）如图，给出下列四组条件：①AB=DE，BC=EF，AC=DF；②AB=DE，∠B=∠E．BC=EF；③∠B=∠E，BC=EF，∠C=∠F；④AB=DE，AC=DF，∠B=∠E．其中，能使△ABC≌△DEF的条件共有（）A.1组B.2组C.3组D.4组【答案】C．解：第①组满足SSS，能证明△ABC≌△DEF．第②组满足SAS，能证明△ABC≌△DEF．第③组满足ASA，能证明△ABC≌△DEF．第④组只是SSA，不能证明△ABC≌△DEF．所以有3组能证明△ABC≌△DEF．故符合条件的有3组．故选：C．类型三、全等三角形判定的实际应用4、如图，公园里有一条“Z字形道路ABCD，其中AB∥CD，在AB，BC，CD三段路旁各有一个小石凳E，M，F，且BE＝CF，M在BC的中点.试判断三个石凳E，M，F是否恰好在一条直线上？为什么？【答案与解析】三个小石凳在一条直线上证明：∵AB 平行CD （已知）∴∠B ＝∠C （两直线平行，内错角相等）∵M 在BC 的中点（已知）∴BM ＝CM （中点定义）在△BME 和△CMF 中BE CF B C BM CM =⎧⎪∠=∠⎨⎪=⎩∴△BME ≌△CMF （SAS ）∴∠EMB ＝∠FMC （全等三角形的对应角相等）∴∠EMF ＝∠EMB ＋∠BMF ＝∠FMC ＋∠BMF ＝∠BMC ＝180°（等式的性质）∴E ，M ，F 在同一直线上【总结升华】对于实际应用问题，首先要能将它化成数学模型，再根据数学知识去解决. 由已知易证△BME ≌△CMF ，可得∠EMB ＝∠FMC ，再由∠EMF ＝∠EMB ＋∠BMF ＝∠FMC ＋∠BMF ＝∠BMC ＝180°得到E ，M ，F 在同一直线上.第二课时【学习目标】1. 了解因式分解的意义,以及它与整式乘法的关系；2． 能确定多项式各项的公因式，会用提公因式法将多项式分解因式.【要点梳理】要点一、因式分解把一个多项式化成几个整式积的形式，叫做把这个多项式因式分解，也叫做把这个多项式分解因式.要点诠释：（1）因式分解只针对多项式，而不是针对单项式，是对这个多项式的整体，而不是部分，因式分解的结果只能是整式的积的形式.（2）要把一个多项式分解到每一个因式不能再分解为止.（3）因式分解和整式乘法是互逆的运算，二者不能混淆.因式分解是一种恒等变形，而整式乘法是一种运算.要点二、公因式多项式的各项中都含有相同的因式，那么这个相同的因式就叫做公因式.要点诠释：（1）公因式必须是每一项中都含有的因式.（2）公因式可以是一个数，也可以是一个字母，还可以是一个多项式.（3）公因式的确定分为数字系数和字母两部分：①公因式的系数是各项系数的最大公约数.②字母是各项中相同的字母，指数取各字母指数最低的. 要点三、提公因式法 把多项式分解成两个因式的乘积的形式，其中一个因式是各项的公因式m ，另一个因式是，即，而正好是除以m 所得的商，这种因式分解的方法叫提公因式法．要点诠释：（1）提公因式法分解因式实际上是逆用乘法分配律，即 .（2）用提公因式法分解因式的关键是准确找出多项式各项的公因式.（3）当多项式第一项的系数是负数时，通常先提出“—”号，使括号内的第一项的系数变为正数，同时多项式的各项都要变号.（4）用提公因式法分解因式时，若多项式的某项与公因式相等或它们的和为零，则提取公因式后，该项变为：“＋1”或“－1”，不要把该项漏掉，或认为是0而出现错误.【典型例题】类型一、因式分解的概念1、下列由左到右的变形，哪些是因式分解？哪些不是？请说明理由．（1）()a x y ax ay +=+；（2）2221(2)(1)(1)x xy y x x y y y ++-=+++-；（3）24(2)(2)ax a a x x -=+-；（4）221122ab a b =； （5）222112a a a a ⎛⎫++=+ ⎪⎝⎭． 【思路点拨】根据因式分解的定义是将多项式形式变成几个整式的积的形式，从对象和结果两方面去判断.【答案与解析】解：因为(1)(2)的右边都不是积的形式，所以它们都不是因式分解；(4)的左边不是多项式而是一个单项式，(5)中的21a 、1a都不是整式，所以(4)(5)也不是因式分解， 只有(3)的左边是多项式，右边是整式的积的形式，所以只有(3)是因式分解．【总结升华】因式分解是将多项式变成积的形式，所以等式的左边必须是多项式，将单项式拆成几个单项式乘积的形式不能称为因式分解．等式的右边必须是整式因式积的形式． 举一反三：【变式】下列变形是因式分解的是 ( )A.243(2)(2)3a a a a a -+=-++B.2244(2)x x x ++=+C. 11(1)x x x +=+D.2(1)(1)1x x x +-=-【答案】B ；类型二、提公因式法分解因式2、下列因式分解变形中，正确的是（ ）A ．()()()()1ab a b a b a a b a b ---=--+B ．()()()()262231m n m n m n m n +-+=+++C ．()()()()232332y x x y y x y x -+-=--+D ．()()()()2232x x y x y x y x y +-+=++ 【答案】A ；【解析】解：A.()()()()1ab a b a b a a b a b ---=--+，正确；B.()()()()2622331m n m n m n m n +-+=++-，故本选项错误；C.()()()()232332y x x y y x y x -+-=---，故本选项错误；D.()()()()223331x x y x y x y x xy +-+=++-，故本选项错误． 【总结升华】解题的关键是正确找出公因式，提取公因式后注意符号的变化．找公因式的要点是：（1）公因式的系数是多项式各项系数的最大公约数；（2）字母取各项都含有的相同字母；（3）相同字母的指数取次数最低的．举一反三：【变式】（2020春•濉溪县期末）下列分解因式结果正确的是（ ）A.a 2b+7ab ﹣b=b （a 2+7a ）B.3x 2y ﹣3xy+6y=3y （x 2﹣x ﹣2）C.8xyz ﹣6x 2y 2=2xyz （4﹣3xy ）D.﹣2a 2+4ab ﹣6ac=﹣2a （a ﹣2b+3c ）【答案】D.解：A 、原式=b （a 2+7a+1），错误；B 、原式=3y （x 2﹣x+2），错误；C 、原式=2xy （4z ﹣3xy ），错误；D 、原式=﹣2a （a ﹣2b+3c ），正确．故选D ．类型三、提公因式法分解因式的应用3、若a 、b 、c 为ABC ∆的三边长，且()()()()a b b a b a a c a b a c -+-=-+-，则ABC ∆按边分类，应是什么三角形？【答案与解析】解：∵()()()()a b b a b a a c a b a c -+-=-+-∴()()()()a b b a a b a c a b c a ---=---()()()()a b b a c a a b --=--当a b =时，等式成立，当a b ≠时，原式变为a b a c -=-，得出b c =，∴a b b c ==或 ∴ABC ∆是等腰三角形.【总结升华】将原式分解因式，就可以得出三边之间的关系，从而判定三角形的类型.4、对任意自然数n （n ＞0），422n n +-是30的倍数，请你判定一下这个说法的正确性，并说说理由.【答案与解析】解：()44422222221152n n n n n n +-=⨯-=-=⨯∵n 为大于0的自然数，∴2n 为偶数，15×2n 为30的倍数，即422n n +-是30的倍数.【总结升华】判断422n n +-是否为30的倍数，只需要把422n n +-分解因式，看分解后有没有能够整除30的因式.举一反三：【变式】说明200199198343103-⨯+⨯能被7整除. 【答案】解：200199198343103-⨯+⨯()198219833431073=-⨯+=⨯ 所以200199198343103-⨯+⨯能被7整除.5、（2020春•湘潭县期末）已知xy=﹣3，满足x+y=2，求代数式x 2y+xy 2的值．【思路点拨】将原式提取公因式xy，进而将已知代入求出结果即可．【答案与解析】解：∵xy=—3，x+y=2，∴x2y+xy2=xy（x+y）=﹣3×2=﹣6．【总结升华】此题主要考查了提取公因式法分解因式，正确找出公因式是解题关键．。

第2节 三角形全等证明之二次全等在证明线段相等或者角相等时,常见的方法是通过证明线段或角所在的三角形全等来证明线段或者角相等.但有的时候,根据题目条件无法简单地通过一次全等证明来得到最终的结论,这时就需要证明两次三角形全等,即证明图中的两对三角形全等.这种方法较多见于对称型全等和旋转型全等的题目中.一、典型例题[例]图2-1是某产品商标的示意图,已知AB ＝CD,∠A ＝∠D,有人认为△ABC ≌△DCB,他的思考过程是:∵AB ＝CD,∠A ＝∠D,BC ＝CB,∴△ABC ≌△DCB.你认为这个思考过程对吗？如果正确,请指出他用的是判定三角形全等的哪个定理？如果不正确,请写出你的思考过程.解:他的思考过程不正确.在△ABE 和△DCE 中,∵{∠AEB =∠DEC∠A =∠D AB =DC∴△ABE ≌△DCE （AAS ）.∴AE ＝DE,BE ＝CE.∴AE+EC ＝DE+EB,即AC ＝BD.在△ABC 和△DCB 中,∴{AC =BDAB =DC BC =CB∴△ABC ≌△DCB （SSS ）.二、培优巩固练习篇1.如图2-2所示,点A,E,C 在一条直线上,∠1＝∠2,∠3＝∠4.求证:△ABE ≌△ADE.图2-2图2-12.如图2-3所示,点A,E,F,C 在一条直线上,AE ＝CF,分别过点E,F 作DE ⊥ AC,BF ⊥AC,连接AB,CD,且AB ∥CD,连接BD 交AC 于点C.求证:△DEG ≌△BFG.3.如图2-4所示,AB ＝AC,DB ＝DC,F 是AD 延长线上的一点.求证:BF ＝CF.4.如图2-5所示,AE 是∠BAC 的角平分线,EB ⊥AB 于点B,EC ⊥AC 于点C,点D 是AE 上一点.求证:BD ＝CD.5.如图2-6所示,DE ⊥AC,BF ⊥AC,AD ＝BC,DE ＝BF.求证:AB ∥DC.图2-3C图2-4图2-5图2-66.如图2-7所示,点E,F 在BD 上,且AB ＝CD,BF ＝DE,AE ＝CF.求证:AO ＝CO.7.如图2-8所示,AB 之间有一条河.想要测量AB 的长,但无法过河接近点A,于是在AB 外任取一点D,在AB 的延长线上任取一点E,连接ED 和BD,并延长BD 到点G,使DG ＝DB,延长ED 到点F,使DF ＝DE,连接FG,并延长FG 到点H,使点H,D,A 在一条直线上,则HG ＝AB.试说明这种测量方法的原理.8.如图2-9所示,在Rt △ABC 和Rt △ADE 中,∠ABC ＝∠ADE ＝90°,BC 与DE 相交于点F,且AB ＝AD,AC ＝AE,连接CD,EB.求证:(1)∠CAD ＝∠EAB;（2）CF ＝EFDH图2-8图2-99.如图2-10所示,在等边△ABC 内取一点D,使DA ＝DB,在△ABC 外取一点E,使∠DBE ＝∠DBC,且BE ＝BA,则∠BED ＝_______°.10.如图2-11所示,∠BAC 是钝角,AB ＝AC,点D,E 分别在AB,AC 上,且CD ＝BE.试说明:∠ADC ＝∠AEB.一个同学的解法是这样的: 在△ACD 和△ABE 中, ∵{AB =AC BE =CD ∠BAE =∠CAD ∴△ABE ≌△ACD.∴∠ADC ＝∠AEB.这种解法遭到了其他同学的质疑.理由是错在不能用“SSA ”判定三角形全等.请你给出正确的解法.图2-10CB AC B答案解析1.证明:在△DEC和△BEC中,{∠1=∠2 EC=EC ∠3=∠4∴△DEC≌△BEC（ASA）.∴DE＝BE.∵∠3＝∠4,∴∠DEA＝∠BEA.在△ABE和△ADE中,{AE=AE∠AEB=∠AEDBE=DE∴△ABE≌△ADE（SAS）.2.证明:∵DE⊥AC,BF⊥AC, ∴∠AFB＝90°＝∠CED. ∵AE＝CF,∴AE+EF＝CF+FE,即AF＝CE.∵AB∥CD,∴∠A＝∠C.在△ABF和△CDE中,{∠A=∠C AF=CE∠AFB=∠CED ∴△ABF≌△CDE（ASA）.∴DE＝BF.在△BFG和△DEG中,{∠BFG=∠DEG ∠BGF=∠DGE BF=DE∴△BFG≌△DEG（AAS）.3.证明:在△ABD和△ACD中,{AB=AC BD=CD AD=AD∴△ABD≌△ACD（SSS）.∴∠BAD＝∠CAD.在△BAF和△CAF中,{AB=AC∠BAF=∠CAF AF=AF∴△BAF≌△CAF（SAS）.∴BF＝CF.4.证明:∵AE是∠BAC的角平分线, ∴∠CAE＝∠BAE. ∵EB⊥AB,EC⊥AC, ∴∠ECA＝∠EBA＝90°.在△CAE和△BAE中,{∠CAE=∠BAE ∠ECA=∠EBA AE=AE∴△CAE≌△BAE（AAS）.∴AC＝AB.在△CAD和△BAD中,{AC=AB ∠CAD＝∠BAD AD=AD∴△CAD≌△BAD（SAS）.∴BD＝CD.5.证明:∵DE ⊥AC,BF ⊥AC, ∴∠AED ＝∠CFB ＝90°, ∠AFB ＝∠CED ＝90°, 在Rt △ADE 和Rt △CBF 中,∵{AD =CB DE =BF ∴Rt △ADE ≌Rt △CBF （HL ）.∴AE ＝CF.∴AE+EF ＝CF+FE,即AF ＝CE.在△AFB 和△CED 中,∵{AF =CE∠AFB =∠CED DE =BF∴△AFB ≌△CED （SAS ）. ∴∠BAF ＝∠DCE.∴AB ∥DC.∴AO ＝CO.6.证明:∵BF ＝DE, ∴BF-EF ＝DE-FE,即BE ＝DF. 在△ABE 和△CDF 中, {AB =CDAE =CF BE =DF∴△ABE ≌△CDF （SSS ）.∴∠B ＝∠D.在△AOB 和△COD 中,{∠AOB =∠COD∠B =∠D AB =CD∴△AOB ≌△COD （AAS ）7.解:在△BED 和△GFD 中,{DB =DG∠BDE =∠GDF DE =DF∴△BED ≌△GFD （SAS ）.∴∠EBD ＝∠FGD.∴∠ABD ＝∠HGD.在△ABD 和△HGD 中,{∠ABD =∠HGDBD =GD∠BDA =∠GDH∴△ABD ≌△HGD （ASA ）.∴HG ＝AB.8.证明:（1）在Rt △ABC 和Rt △ADE 中,{AC =AE AB =AD ∴Rt △ABC ≌Rt △ADE （HL ）.∴∠BAC ＝∠DAE.∴∠BAC-∠DAB ＝∠DAE-∠DAB,即∠CAD ＝∠EAB.（2）在△ACD 与△AEB 中, {AC =AE∠CAD =∠EAB AD =AB∴△ACD ≌△AEB （SAS ）.∴CD ＝BE,∠ACD ＝∠AEB.∵Rt △ABC ≌Rt △ADE （HL ）, ∴∠ACB ＝∠AED.∴∠ACB-∠ACD ＝∠AED-∠AEB,即∠DCF ＝∠BEF.又∵∠DFC ＝∠BFE, ∴△DFC ≌△BFE （AAS ）.∴CF ＝EF.9.解:如图2所示,连接CD.∵△ABC是等边三角形, ∴AB＝BC＝CA.∵BE＝BA,BA＝BC, ∴BE＝BC.在△BDC和△BDE中,{BD=BD∠DBE=∠DBC BE=BC∴△BDC≌△BDE（SAS）. ∴∠BED＝∠BCD.在△BCD和△ACD中,{BC=AC BD=AD CD=CD∴△BCD≌△ACD（SSS）.∴∠BCD＝∠ACD＝30°.∴∠BED＝30°.10.证明:因为∠BAC是钝角,故过点B,C分别作CA,BA的垂线,垂足分别为点F, G,如图3所示.在△ABF和△ACG中,{∠F=∠G=90°∠FAB=∠GACAC=AB∴△ABF≌△ACG（AAS）.∴BF＝CG.在Rt△BEF和Rt△CDG中,{BF=CGBE=CD∴Rt△BEF≌Rt△CDG（HL）.∴∠ADC＝∠AEBEDC BA。

三角形全等的条件练习1. 如图，ABC △中，AB AC =，EB EC =，则由“SSS ”可以判定（ ） Ａ．ABD ACD △≌△ Ｂ．ABE ACE △≌△ Ｃ．BDE CDE △≌△ Ｄ．以上答案都不对2. 如图，ABC △中，AB AC =，AE CF =，BE AF =，则E ∠=∠________，CAF ∠=∠__________．1题 2题第3题. 如图，AD BC =，DC AB =，AE CF =，找出图中的一对全等三角形，并说明你的理由．．第4题. 如图，ABC △是等边三角形，若在它边上的一点与这边所对角的顶点的连线恰好将ABC △分成两个全等三角形，则这样的点共有（ ） Ａ．1个 Ｂ．3个 Ｃ．6个 Ｄ．9个第5题. 如图，已知A D ∠=∠，AB CD =．求证：ABO DCO △≌△．第6题. 如图，点D E ，分别在AB AC ，上，且AD AE =，BDC CEB ∠=∠．求证：BD CE =．AB D CA E FC BA C F D EB AB C A D O BC ADE BC求证：（1）ADC ABE ∠=∠；（2）DC BE =．第8题. 如图，已知ABC △为等边三角形，QR AB ⊥，垂足为R ，PQ AC ⊥，垂足为Q ，RP BC ⊥，垂足为P ，且AR BP CQ ==．求证：RPQ △为等边三角形．第9题. 如图，已知点A C ，在EF 上，AD BC =，AD BC ∥，DE BF ∥．求证：DE BF =．第10题. 如图，在ABC △和DEF △中，已知AB DE =，BC EF =，根据（SAS ）判定ABC DEF △≌△，还需的条件是（ ） Ａ．A D ∠=∠ Ｂ．B E ∠=∠ Ｃ．C F ∠=∠Ｄ．以上三个均可以A BED C1 23 4ARB PC QF CD E A B A D B C E FＡ．两边一夹角 Ｂ．两角一夹边 Ｃ．三边 Ｄ．三角 第12题. 如图，已知AB BD ⊥，垂足为B ，ED BD ⊥，垂足为D ，AB CD =，BC DE =，则A C E ∠＝___________．第13题. 如图，已知AB AC =，AD AE =，BAC DAE ∠=∠．求证：BD CE =．第14题. 下列各命题中，真命题是（ ）Ａ．如果两个三角形面积不相等，那么这两个三角形不可能全等 Ｂ．如果两个三角形不全等，那么这两个三角形面积一定不相等Ｃ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP △与EFG △的面积的和等于M N P '''△与E F G '''△面积的和Ｄ．如果MNP EFG △≌△，M N P E F G ''''''△≌△，那么MNP M N P EFG E F G ''''''△+△≌△+△ 第15题. 如图，已知AF BE =，A B ∠=∠，AC BD =．求证：F E ∠=∠．第16题. 如图，点P 是AOB ∠的平分线上的一点，作PD OA ⊥，垂足为D ，PE OB ⊥垂足为E ，DE 交OC 于点F ．（1）你能找到几对全等三角形？请说明理由；（2）你能确定图中共有几个直角吗？请说明理由．AE C B D A E DB C CD A BEF O E B A CD F P的延长线于F ．求证：OE OF =．第18题. 如图，已知AB CD =，AE DF =，CE BF =．求证：AF DE =．第19题. 对于下列各组条件，不能判定ABC A B C '''△≌△的一组是（ ） Ａ．A A '∠=∠，B B '∠=∠，AB A B ''= Ｂ．A A '∠=∠，AB A B ''=，AC A C ''= Ｃ．A A '∠=∠，AB A B ''=，BC B C ''= Ｄ．AB A B ''=，AC A C ''=，BC B C ''=第21题. 如图，已知在ABC △和A B C '''△中，AM 与A M ''分别是BC B C ''，上的中线，AB A B ''=，AC A C ''=，AM A M ''=．求证：ABC A B C '''△≌△． ．第22题. 如图，已知在ABC △中，AB AC =，12∠=∠．求证：AD BC ⊥，BD DC =．A BF E C DA B M C A ' B ' M ' C ' A B C D 21 3 4B '，使OB BO '=，延长CO 到C '，使OC CO '=，得到A B C '''△，A B C '''△与ABC △是否全等？这两个三角形的对应边是否平行？为什么？第24题. 如图，在ABC △中，90C ∠=，D E ，分别为AC AB ，上的点，且AD BD =，AE BC =，DE DC =．求证：DE AB ⊥．第25题. 如图，AB AC =，要使△ABE ≌△ACD ，应添加的条件是 ，（添加一个条件即可）第26题. 如图，四边形ABCD 中，AC 垂直平分BD ，垂足为点O ． （1）图中有多少对全等三角形？请把它们都写出来；（2）任选（1）中的一对全等三角形加以证明．OABCC 'A 'B 'EADBC AD B OECA B D C O件（ ）A ．AB ED = B ．AB FD =C ．AC FD = D ．A F ∠=∠第28题. 小明用四根竹棒扎成如图所示的风筝框架，已知AB CD =，AD CB =，你认为小明的风筝两脚大小相同吗（即B ∠，D ∠相等吗）？请说明理由．第29题. 小民用五根木条钉成了如图所示的两个三角形，且AB AC =，BD CD =，若ABD △为锐角三角形，则ACD △中的最大角α的取范围是（ ）Ａ．3060<α≤ Ｂ．4560<α≤ Ｃ．4590<α≤Ｄ．6090<α≤第30题. 已知：ABC △的三边分别为a b c ，，，A B C '''△的三边分别为a b c '''，，，且有222222222a a b b c c a b b c ca ''''''+++++=++，则ABC △与A B C '''△（ ） Ａ．一定全等 Ｂ．不一定全等 Ｃ．一定不全等 Ｄ．无法确定第31题. 如图，已知12∠=∠，34∠=∠．求证：BE CD =．第32题. 你见过形如图所示的风筝吗？开始制作时，AB CD =，AC DB =，后来为了加固，又过点O 加了一根竹棒EF ，分别交AB CD ，于点E F ，，且AOE DOF ∠=∠，你认为OE OF ，相等吗？请说明理由．A B DCO AC D B AB CDA1 2 3 4 D E B CA D F E OB C．第34题. 如图，已知12∠=∠，ABC DCB ∠=∠，AC DB =．求证：ABC DCB △≌△． ．第35题. 在ABC △和A B C ''△中，①AB A B ''=；②BC B C ''=；③AC A C ''=；④A A '∠=∠；⑤B B '∠=∠则下列条件中不能保证ABC A B C '''△≌△的是（ ） Ａ．①②③ Ｂ．①②⑤ Ｃ．②④⑤ Ｄ．①③⑤第37题. 如图，AB AC BE =，与CF 交于点O ，EC FB 与相等吗？为什么？第38题. 如图，AB DC AB DC AC BD =∥，，与相交于点O ，你能找出两对全等的三角形吗？你能说明其中的道理吗？AB OCD 2 A D C B 1 ABCDO第39题. 已知：如图，D 是△ABC 的边AB 上一点，AB FC ∥，DF AC E 交于点，DE FE =．AE CE =求证:．第40题. 如图，给出五个等量关系：①AD BC =、②AC BD =、③CE DE =、④D C ∠=∠、⑤DAB CBA ∠=∠．请你以其中两个为条件，另三个中的一个为结论，推出一个正确的命题（只需写出一种情况），并加以证明． 已知：求证：证明：第41题. 如图，A B ，两点分别位于池塘两端，小明和同伴用下面的方法测量AB 间的距离：先在地上取一个可以直接到达A 点和B 点的点C ，连接AC 并延长到D ，使CD AC =，连接BC 并延长到E ，使CE BC =，连接DE ，那么量出DE 的长，就是A B ，的距离，小明和同伴的测量方法对不对？为什么？第42题. 如图，要测量河两岸相对的两点A ，B 的距离，可以在AB 的垂线BF 上取两点C D ，，使CD BC =，再定出BF 的垂线DE ，使A C E ，，在一条直线上，这时测得的DE 的长就是AB 的长，为什么？ AD B C FEA B C E DA B C E D C D F E A B第43题. 如图A B ，两个建筑分别位于河的两岸，要测得它们之间的距离，可以从B 出发沿河岸画一条射线BF ，在BF 上截取BC CD =，过D 作DE AB ∥，使E C A ，，在同一条直线上，则DE 的长就是A B ，之间的距离．请你说明道理．你还能想出其他方法吗？第44题. 如图，已知90B D ∠=∠=，AB AD =．求证：BC DC =．．第45题. 如图，已知AD AF ，分别是两个钝角ABC △和ABE △的高，如果AD AF =，AC AE =． 求证：BC BE =．第46题. 使两个直角三角形全等的条件是（ ） Ａ．一个锐角对应相等 Ｂ．两个锐角对应相等 Ｃ．一条边对应相等 Ｄ．两条直角边对应相等第47题. 如图，有一正方形窗架，盖房时为了稳定，在上面钉了两个等长的木条GF 与GE E F ，，分别是AD BC ，的中点，G 是AB 的中点吗？AB C F E D A CD B A D C BE F A B CF E D G第48题. 如图，已知A F E B ，，，四点共线，AC CE ⊥，BD DF ⊥，AE BF =，AC BD =． 求证：ACF BDE △≌△．第49题. 判定两个直角三角形全等的方法有 Ａ．两条直角边对应相等 Ｂ．斜边和一锐角对应相等 Ｃ．斜边和一条直角边对应相等 Ｃ．两个面积相等其中不正确的为（ ）第50题. 将一张矩形纸片沿对角线剪开，得到两张三角形纸片，再将这两张三角形纸片摆放成如下右图的形式，使点B ，F ，C ，D 在同一条直线上． （1）求证：AB ED ⊥；（2）若PB BC =，请找出图中与此条件有关的一对．．全等三角形，并给予证明．A F DE BC AEPM BF CDNACBD FE。

2022年人教版初中数学8年级上册【巩固练习】一、选择题1.（2020•奉贤区二模）如图，已知AD是△ABC的边BC上的高，下列能使△ABD≌△ACD的条件是（）A．∠B=45° B.∠BAC=90° C.BD=AC D．AB=AC2.如图，已知AB＝CD，AD＝BC，则下列结论中错误的是（）A.AB∥DCB.∠B＝∠DC.∠A＝∠CD.AB＝BC3.下列判断正确的是（）A.两个等边三角形全等B.三个对应角相等的两个三角形全等C.腰长对应相等的两个等腰三角形全等D.直角三角形与锐角三角形不全等4.如图，AB、CD、EF相交于O，且被O点平分，DF＝CE，BF＝AE，则图中全等三角形的对数共有（）A.1对B.2对C.3对D.4对5．如图，∠1＝∠2，∠3＝∠4，下面结论中错误的是（）A．△ADC≌△BCD B．△ABD≌△BACC．△ABO≌△CDO D．△AOD≌△BOC6.如图，已知AB⊥BD于B，ED⊥BD于D，AB＝CD，BC＝ED，以下结论不正确的是（）A.EC⊥ACB.EC＝ACC.ED＋AB＝DBD.DC＝CB二、填空题7.如图，AB＝CD，AC＝DB，∠ABD＝25°，∠AOB＝82°，则∠DCB＝_________.8.如图,已知：∠1＝∠2,∠3＝∠4,要证BD＝CD,需先证△AEB≌△AEC,根据是，再证△BDE≌△，根据是．9.（2020秋•大同期末）如下图∠1=∠2，由AAS判定△ABD≌△ACD，则需添加的条件是．10.如图，AC＝AD，CB＝DB，∠2＝30°，∠3＝26°，则∠CBE＝_______.11.如图，点D在AB上，点E在AC上，CD与BE相交于点O，且AD＝AE，AB＝AC，若∠B＝20°，则∠C＝_______．12.已知，如图，AB＝CD，AC＝BD，则△ABC≌，△ADC≌.三、解答题13.（2020•通辽）如图，四边形ABCD中，E点在AD上，其中∠BAE=∠BCE=∠ACD=90°，且BC=CE，求证：△ABC与△DEC全等．14.如图，已知D、E、B三点共线，AE=CE,AE⊥CE，∠D=∠B=90°．求证：CD+AB=DB．15.如图，已知AB＝DC，AC＝DB，BE＝CE求证：AE＝DE.【答案与解析】一.选择题1.【答案】D；【解析】解：当AB=AC时，△ABD≌△ACD，∵AD是△ABC的边BC上的高，AB=AC，∴BD=CD，∵在△ABD 和△ADC 中，∴△ABD≌△ACD（SSS）.2.【答案】D；【解析】连接AC 或BD 证全等.3.【答案】D；4.【答案】C；【解析】△DOF≌△COE，△BOF≌△AOE，△DOB≌△COA.5.【答案】A；【解析】将两根钢条'AA ，'BB 的中点O 连在一起，说明OA＝'OA ，OB＝'OB ，再由对顶角相等可证.6.【答案】D；【解析】△ABC≌△EDC，∠ECD＋∠ACB＝∠CAB＋∠ACB＝90°，所以EC⊥AC，ED ＋AB ＝BC＋CD＝DB.二.填空题7.【答案】66°；【解析】可由SSS 证明△ABC≌△DCB，∠OBC＝∠OCB＝82412︒=︒，所以∠DCB＝∠ABC＝25°＋41°＝66°.8.【答案】ASA，CDE，SAS；【解析】△AEB ≌△AEC 后可得BE＝CE.9.【答案】∠B=∠C．【解析】解：由图可知，只能是∠B=∠C，才能组成“AAS”．故填∠B=∠C．10.【答案】56°；【解析】∠CBE＝26°＋30°＝56°.11.【答案】20°；【解析】△ABE≌△ACD（SAS）.12.【答案】△DCB，△DAB；【解析】注意对应顶点写在相应的位置上.三.解答题13.【解析】解：∵∠BCE=∠ACD=90°，∴∠3+∠4=∠4+∠5，∴∠3=∠5，在△ACD 中，∠ACD=90°，∴∠2+∠D=90°，∵∠BAE=∠1+∠2=90°，∴∠1=∠D，在△ABC 和△DEC 中，，∴△ABC≌△DEC（AAS）．14.【解析】证明：∵AE⊥CE，∴∠AEB+∠CED=90°，又∵∠B=90°∴∠A+∠AEB=90°，∴∠A=∠CED，在△AEB 与△ECD 中，A CEDB DAE CE ∠=∠∠=∠=⎧⎪⎨⎪⎩∴△AEB≌△ECD（AAS）∴AB=DE ，BE=CD∵DE+BE=DB∴CD+AB=DB15.【解析】证明：在△ABC 和△DCB 中AB DC AC DB BC =CB ⎧⎪⎨⎪⎩＝＝∴△ABC≌△DCB（SSS）∴∠ABC＝∠DCB，在△ABE 和△DCE 中ABC DCB AB DC BE CE =∠=∠=⎧⎪⎨⎪⎩∴△ABE≌△DCE（SAS）∴AE＝DE.全等三角形的判定二（SSS，AAS）（基础）【学习目标】1．理解和掌握全等三角形判定方法3——“边边边”，和判定方法4——“角角边”；2．能把证明角相等或线段相等的问题，转化为证明它们所在的两个三角形全等.【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS”）.要点诠释：如图，如果''A B ＝AB，''A C ＝AC，''B C ＝BC，则△ABC≌△'''A B C .要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）要点诠释：由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等，也就是说，用角边角条件可以证明角角边条件，后者是前者的推论.2.三个角对应相等的两个三角形不一定全等.如图，在△ABC 和△ADE 中，如果DE∥BC，那么∠ADE＝∠B，∠AED＝∠C，又∠A＝∠A，但△ABC 和△ADE 不全等.这说明，三个角对应相等的两个三角形不一定全等.要点三、判定方法的选择1.选择哪种判定方法，要根据具体的已知条件而定，见下表：已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SAS SSS2.如何选择三角形证全等（1）可以从求证出发，看求证的线段或角（用等量代换后的线段、角）在哪两个可能全等的三角形中，可以证这两个三角形全等；（2）可以从已知出发，看已知条件确定证哪两个三角形全等；（3）由条件和结论一起出发，看它们一同确定哪两个三角形全等，然后证它们全等；（4）如果以上方法都行不通，就添加辅助线，构造全等三角形.【典型例题】类型一、全等三角形的判定3——“边边边”1、已知：如图，△RPQ 中，RP＝RQ，M 为PQ 的中点．求证：RM平分∠PRQ．【思路点拨】由中点的定义得PM＝QM，RM 为公共边，则可由SSS 定理证明全等.【答案与解析】证明：∵M 为PQ 的中点（已知），∴PM＝QM在△RPM 和△RQM 中，()(),,RP RQ PM QM RM RM ⎧=⎪=⎨⎪=⎩已知公共边∴△RPM≌△RQM（SSS）．∴∠PRM＝∠QRM（全等三角形对应角相等）．即RM 平分∠PRQ.【总结升华】在寻找三角形全等的条件时有的可以从图中直接找到，如：公共边、公共角、对顶角等条件隐含在题目或图形之中.把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的性质和判定.举一反三：【变式】已知：如图，AD＝BC，AC＝BD.试证明：∠CAD＝∠DBC.【答案】证明：连接DC，在△ACD 与△BDC 中()AD BC AC BD CD DC ⎧=⎪=⎨⎪=⎩公共边∴△ACD≌△BDC（SSS）∴∠CAD＝∠DBC（全等三角形对应角相等）类型二、全等三角形的判定4——“角角边”2、已知：如图，AB⊥AE，AD⊥AC，∠E＝∠B，DE＝CB．求证：AD＝AC．【思路点拨】要证AC＝AD，就是证含有这两个线段的三角形△BAC≌△EAD.【答案与解析】证明：∵AB⊥AE，AD⊥AC，∴∠CAD＝∠BAE＝90°∴∠CAD＋∠DAB＝∠BAE＋∠DAB ，即∠BAC＝∠EAD在△BAC 和△EAD 中BAC EAD B E CB=DE ∠=∠⎧⎪∠=∠⎨⎪⎩∴△BAC≌△EAD（AAS）∴AC＝AD【总结升华】我们要善于把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．举一反三：【变式】如图，AD 是△ABC 的中线，过C、B 分别作AD 及AD 的延长线的垂线CF、BE.求证：BE＝CF.【答案】证明：∵AD 为△ABC 的中线∴BD＝CD∵BE⊥AD，CF⊥AD，∴∠BED＝∠CFD＝90°，在△BED 和△CFD 中BED CFD BDE CDF BD CD ∠=∠⎧⎪∠=∠⎨⎪=⎩（对顶角相等）∴△BED≌△CFD（AAS）∴BE＝CF3、（2020春•雅安期末）如图：AB=A′B′，∠A=∠A′，若△ABC≌△A′B′C′，则还需添加的一个条件有（）种．A.1B.2C.3D.4【思路点拨】本题要证明△ABC≌△A′B′C′，已知了AB=A′B′，∠A=∠A′，可用的判别方法有ASA，AAS，及SAS，所以可添加一对角∠B=∠B′，或∠C=∠C′，或一对边AC=A′C′，分别由已知与所添的条件即可得证．【答案与解析】解：添加的条件可以为：∠B=∠B′；∠C=∠C′；AC=A′C′，共3种．若添加∠B=∠B′，证明：在△ABC 和△A′B′C′中，，∴△ABC≌△A′B′C′（ASA）；若添加∠C=∠C′，证明：在△ABC 和△A′B′C′中，，∴△ABC≌△A′B′C′（AAS）；若添加AC=A′C′，证明：在△ABC 和△A′B′C′中，，∴△ABC≌△A′B′C′（SAS）．故选C.【总结升华】此题考查了全等三角形的判定，是一道条件开放型问题，需要由因索果，逆向推理，逐步探求使结论成立的条件，解决这类问题要注意挖掘隐含的条件，如公共角、公共边、对顶角相等，这类问题的答案往往不唯一，只有合理即可．熟练掌握全等三角形的判定方法是解本题的关键．类型三、全等三角形判定的实际应用4、“三月三，放风筝”．下图是小明制作的风筝，他根据DE＝DF，EH＝FH，不用度量，就知道∠DEH＝∠DFH．请你用所学的知识证明．【答案与解析】证明：在△DEH 和△DFH 中，DE DF EH FH DH DH ⎧⎪⎨⎪=⎩＝＝∴△DEH≌△DFH(SSS)∴∠DEH＝∠DFH．【总结升华】证明△DEH≌△DFH，就可以得到∠DEH＝∠DFH，我们要善于从实际问题中抽离出来数学模型，这道题用“SSS”定理就能解决问题.举一反三：【变式】（2020秋•紫阳县期末）雨伞的中截面如图所示，伞骨AB=AC，支撑杆OE=OF，AE=AB，AF=AC，当O 沿AD 滑动时，雨伞开闭，问雨伞开闭过程中，∠BAD 与∠CAD 有何关系？说明理由．【答案】解：雨伞开闭过程中二者关系始终是：∠BAD=∠CAD，理由如下：∵AB=AC，AE=AB，AF=AC，∴AE=AF，在△AOE 与△AOF 中，，∴△AOE≌△AOF（SSS），∴∠BAD=∠CAD．【巩固练习】一、选择题1．如图，∠A＝∠D，∠B＝∠E，BF＝CE，下列结论错误的是（）A.△ABC≌△DEFB.BF＝ECC.AC∥DED.AC＝DF2．如图，AB∥EF，DE∥AC，BD＝CF，则图中不是全等三角形的是（）A.△BAC≌FEDB.△BDA≌FCEC.△DEC≌CADD.△BAC≌FCE3．如图，AB＝BD，∠1＝∠2，要用AAS判定△ABC≌△DBE，则添加的条件是（）A.AE＝ECB.∠D＝∠AC.BE＝BCD.∠DEB＝∠C4．下列判断中错误的是（）A.有两角和一边对应相等的两个三角形全等B.有两边和一角对应相等的两个三角形全等C.有两边和其中一边上的中线对应相等的两个三角形全等D.有一边对应相等的两个等边三角形全等5．（2020•滕州市校级模拟）如图，在下列条件中，不能证明△ABD≌△ACD的是（）A．BD=DC，AB=AC B．∠ADB=∠ADC，BD=DCC．∠B=∠C，∠BAD=∠CAD D．∠B=∠C，BD=DC6．如图，点A在DE上，AC＝CE，∠1＝∠2＝∠3，则DE的长等于（）A．DC B．BC C．AB D．AE＋AC二、填空题7．（2020春•鹤岗校级期末）如图：在△ABC和△FED中，AD=FC，AB=FE，当添加条件________________时，就可得到△ABC≌△FED．（只需填写一个即可）8．如图，点D在AB上，点E在AC上，且∠B＝∠C，在条件①AB＝AC，②AD＝AE，③BE＝CD，④∠AEB＝∠ADC中，不能使△ABE≌△ACD的是_______.（填序号）9．已知，如图，AB∥CD，AF∥DE，AF＝DE，且BE＝2，BC＝10，则EF＝________.10．如图，AB∥CD，AD∥BC，OE＝OF，图中全等三角形共有______对.11．如图，直线l过正方形ABCD的顶点B，点A、C到直线l的距离分别是1和2，则EF的长是___________．12．在△ABC 和△DEF 中（1）AB＝DE；（2）BC＝EF；（3）AC＝DF；（4）∠A＝∠D；（5）∠B＝∠E；（6）∠C＝∠F 从这六个条件中选取三个条件可判定△ABC 与△DEF 全等的方法共有________种.三、解答题13．（2020秋•景洪市校级期中）如图，O 为码头，A，B 两个灯塔与码头的距离相等，OA，OB 为海岸线，一轮船离开码头，计划沿∠AOB 的平分线航行，在航行途中，测得轮船与灯塔A 和灯塔B 的距离相等，试问轮船航行时是否偏离预定航线，请说明理由．14．已知：如图，ABC △中，45ABC ∠=°，CD AB ⊥于D ，BE AC ⊥于E ，BE 与CD 相交于点F ．求证：BF AC =.15．如图，DC∥AB，∠BAD 和∠ADC 的角平分线相交于E，过E 的直线分别交DC、AB 于C、B 两点.求证：AD＝AB＋DC.【答案与解析】一、选择题1．【答案】C；2．【答案】D；3．【答案】D；【解析】满足判定定理AAS的只有D选项.4．【答案】B；【解析】C选项和D选项都可以由SSS定理证全等.5．【答案】D；【解析】解：A、∵在△ABD和△ACD中，∴△ABD≌△ACD（SSS），故本选项错误；B、∵在△ABD和△ACD中，∴△ABD≌△ACD（SAS），故本选项错误；C、∵在△ABD和△ACD中，∴△ABD≌△ACD（AAS），故本选项错误；D、不符合全等三角形的判定定理，不能推出△ABD≌△ACD，故本选项正确；故选D．6．【答案】C；【解析】可证∠BAC＝∠E，∠BCA＝∠DCE，所以△ABC≌△EDC，DE＝AB.二、填空题7．【答案】BC=ED.8．【答案】④【解析】三个角对应相等不能判定三角形全等.9．【答案】6；【解析】△ABF≌△CDE，BE＝CF＝2，EF＝10－2－2＝6.10．【答案】6；【解析】△ABO≌△CDO，△AFO≌△CEO，△DFO≌△BEO，△AOD≌△COB，△ABD≌△CDB，△ABC≌△CDA.11．【答案】3；【解析】由AAS证△ABF≌△CBE，EF＝FB＋BE＝CE＋AF＝2＋1＝3.12．【答案】13；【解析】ASA类型3种，AAS类型6种，SAS类型3种，SSS类型一种，共13种.三、解答题13．【解析】解：此时轮船没有偏离航线．理由：由题意知：假设轮船在D处，则DA=DB，AO=BO，在△ADC和△BDC中，，∴△ADO≌△BDO（SSS），∴∠AOD=∠BOD，即DO 为∠AOB 的角平分线，∴此时轮船没有偏离航线．14．【解析】证明：∵CD AB⊥∴90BDC CDA ∠=∠=︒∵45ABC ∠=︒∴45DCB ABC ∠=∠=︒∴DB DC=∵BE AC⊥∴90AEB ∠=︒∴90A ABE ∠+∠=︒∵90CDA ∠=︒∴90A ACD ∠+∠=︒∴ABE ACD∠=∠在BDF ∆和CDA ∆中BDC CDADB DC ABE ACD∠=∠⎧⎪=⎨⎪∠=∠⎩∴BDF ∆≌CDA ∆（AAS）∴BF AC =.15．【解析】证明：延长DE 交AB 的延长线于F∴∠CDE＝∠F,∠CDA＋∠BAD＝180º∵DE 平分∠CDA,AE 平分∠DAB ∴∠CDE＝∠ADE＝21∠CDA,∠DAE＝∠EAF＝21∠BAD∴∠ADE＝∠F,∠EDA＋∠DAE＝90º∴∠AED＝∠AEF＝90º在△ADE 与△AFE 中⎪⎩⎪⎨⎧=∠=∠∠=∠AE AE FEA DEA F ADE ∴△ADE≌△AFE （AAS）∴DE＝EF,AD＝AF在△DCE 与△FBE 中，⎪⎩⎪⎨⎧∠=∠=∠=∠FEB DEC FE DE F CDE ∴△DCE≌△FBE（ASA）∴DC＝BF，∴AD＝AB＋DC.全等三角形的判定二（SSS，AAS）（提高）【学习目标】1．理解和掌握全等三角形判定方法3——“边边边”，和判定方法4——“角角边”；2．能把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等．【要点梳理】要点一、全等三角形判定3——“边边边”全等三角形判定1——“边边边”三边对应相等的两个三角形全等.（可以简写成“边边边”或“SSS”）．要点诠释：如图，如果''A B ＝AB，''A C ＝AC，''B C ＝BC，则△ABC≌△'''A B C．要点二、全等三角形判定4——“角角边”1.全等三角形判定4——“角角边”两个角和其中一个角的对边对应相等的两个三角形全等（可以简写成“角角边”或“AAS”）要点诠释：由三角形的内角和等于180°可得两个三角形的第三对角对应相等.这样就可由“角边角”判定两个三角形全等，也就是说，用角边角条件可以证明角角边条件，后者是前者的推论．2.三个角对应相等的两个三角形不一定全等.如图，在△ABC 和△ADE 中，如果DE∥BC，那么∠ADE＝∠B，∠AED＝∠C，又∠A＝∠A，但△ABC 和△ADE 不全等.这说明，三个角对应相等的两个三角形不一定全等．要点三、判定方法的选择1.选择哪种判定方法，要根据具体的已知条件而定，见下表：已知条件可选择的判定方法一边一角对应相等SAS AAS ASA 两角对应相等ASA AAS 两边对应相等SASSSS2.如何选择三角形证全等（1）可以从求证出发，看求证的线段或角（用等量代换后的线段、角）在哪两个可能全等的三角形中，可以证这两个三角形全等；（2）可以从已知出发，看已知条件确定证哪两个三角形全等；（3）由条件和结论一起出发，看它们一同确定哪两个三角形全等，然后证它们全等；（4）如果以上方法都行不通，就添加辅助线，构造全等三角形．【典型例题】类型一、全等三角形的判定3——“边边边”1、如图，在△ABC 和△ADE 中，AB＝AC，AD＝AE，BD＝CE，求证：∠BAD＝∠CAE．【答案与解析】证明：在△ABD 和△ACE 中，AB AC AD AE BD CE =⎧⎪=⎨⎪=⎩∴△ABD≌△ACE（SSS）∴∠BAD＝∠CAE（全等三角形对应角相等）．【总结升华】把证明一对角或线段相等的问题，转化为证明它们所在的两个三角形全等，综合应用全等三角形的判定和性质.要证∠BAD＝∠CAE，先找出这两个角所在的三角形分别是△BDA 和△CAE，然后证这两个三角形全等．【变式】（2020•静海县模拟）已知点A、D、C、F 在同一条直线上，AB=DE，BC=EF，要使△ABC≌△DEF，还需添加一个条件是．【答案】AC=DF.解：理由是：∵在△ABC 和△DEF中，∴△ABC≌△DEF（SSS），故答案为：AC=DF．类型二、全等三角形的判定4——“角角边”2、已知：如图，∠ACB＝90°，AC＝BC，CD 是经过点C 的一条直线，过点A、B 分别作AE⊥CD、BF⊥CD，垂足为E、F．求证：CE＝BF【答案与解析】证明：∵AE⊥CD、BF⊥CD，∴∠AEC＝∠BFC＝90°∴∠BCF＋∠B＝90°∵∠ACB＝90°，∴∠BCF＋∠ACF＝90°∴∠ACF＝∠B在△BCF 和△CAE 中⎪⎩⎪⎨⎧=∠=∠∠=∠BC AC B ACE BFC AEC ∴△BCF≌△CAE（AAS）∴CE＝BF．【总结升华】要证CE＝BF，只需证含有这两个线段的△BCF≌△CAE.同角的余角相等是找角3、平面内有一等腰直角三角板（∠ACB＝90°）和一直线MN．过点C 作CE⊥MN 于点E，过点B 作BF⊥MN 于点F．当点E 与点A 重合时（如图1），易证：AF＋BF＝2CE．当三角板绕点A 顺时针旋转至图2的位置时，上述结论是否仍然成立？若成立，请给予证明；若不成立，线段AF、BF、CE之间又有怎样的数量关系，请直接写出你的猜想，不需证明．【思路点拨】过B 作BH⊥CE 与点H，易证△ACE≌△CBH，根据全等三角形的对应边相等，即可证得AF＋BF＝2CE．【答案与解析】解：图2，AF＋BF＝2CE 仍成立，证明：过B 作BH⊥CE 于点H，∵∠CBH＋∠BCH＝∠ACE＋∠BCH＝90°∴∠CBH＝∠ACE在△ACE 与△CBH 中，90ACH CBH AEC CHB AC BC ∠=∠⎧⎪∠=∠=︒⎨⎪=⎩∴△ACE≌△CBH．（AAS）∴CH＝AE，BF＝HE，CE＝EF，∴AF＋BF＝AE＋EF＋BF＝CH＋EF＋HE＝CE＋EF＝2EC．【总结升华】正确作出垂线，构造全等三角形是解决本题的关键．举一反三：【变式】已知Rt△ABC 中，AC＝BC，∠C＝90°，D 为AB 边的中点，∠EDF＝90°，∠EDF 绕D 点旋转，它的两边分别交AC、CB 于E、F．当∠EDF 绕D 点旋转到DE⊥AC 于E 时（如图1），易证12DEF CEF ABC S S S +=△△△；当∠EDF 绕D 点旋转到DE 和AC 不垂直时，在图2情况下，上述结论是否成立？若成立，请给予证明；若不成立，请写出你的猜想，不需证明．图2ADBC E M N F 【答案】解：图2成立；证明图2：过点D 作DM AC DN BC⊥⊥，则90DME DNF MDN ∠=∠=∠=°在△AMD 和△DNB 中，AMD=DNB=90A B AD BD ∠∠︒⎧⎪∠=∠⎨⎪=⎩∴△AMD≌△DNB（AAS）∴DM＝DN∵∠MDE＋∠EDN＝∠NDF＋∠EDN＝90°，∴∠MDE＝∠NDF在△DME 与△DNF 中，90EMD FDN DM DN MDE NDF ∠=∠=︒⎧⎪=⎨⎪∠=∠⎩∴△DME≌△DNF（ASA）∴DME DNFS S =△△∴DEF CEF DMCN DECF S =S =S S .+△△四边形四边形可知ABC DMCN 1S =S 2△四边形，∴12DEF CEF ABC S S S +=△△△．类型三、全等三角形判定的实际应用4、（2020秋•内丘县期中）如图，AD 是一段斜坡，AB 是水平线，现为了测斜坡上一点D 的竖直高度DB 的长度，欢欢在D 处立上一竹竿CD，并保证CD⊥AD，然后在竿顶C 处垂下一根绳CE，与斜坡的交点为点E，他调整好绳子CE 的长度，使得CE=AD，此时他测得DE=2米，求DB 的长度．【思路点拨】延长CE交AB于F，根据等角的余角相等求出∠A=∠C，再利用“角角边”证明△ABD和△CDE全等，根据全等三角形对应边相等可得DB=DE．【答案与解析】解：如图，延长CE交AB于F，则∠A+∠1=90°，∠C+∠2=90°，∵∠1=∠2（对顶角相等），∴∠A=∠C，在△ABD和△CDE中，，∴△ABD≌△CDE（AAS），∴DB=DE，∵DE=2米，∴DB的长度是2米．【总结升华】本题考查了全等三角形的应用，仔细观察图形求出∠A=∠C是解题的关键.。