高数重修试题答案2-1A09-10第一学期

⾼数重修试题⼀（1）设k j i b k j i a 42,253++=-+=，问λ和µ有什么的关系，能使得b aµλ+与z 轴垂直？（2）已知k i OA 3+=，k j OB 3+=，求OAB ?的⾯积。

（3）已知23,3,2,1,,3A a bB a b a b a b π=+=-===求,BA B prj A ?（4）设向经,522k j i M O ++=从点)1,2,1(P 出发，向M O 作垂线PQ ,求向量Q P和长度。

（5）分别画出223yx z +-=,2211y x z ---=⽅程所表⽰的曲⾯。

（6）求上半球2220yx a z --≤≤与圆柱体)0(22>≤+a axy x 的公共部分在xoy 坐标⾯上的投影。

（7）求两平⾯012=+-+z y x 和012=-++-z y x ⾓平分⾯的⽅程。

42012=--+=--+z y x z y x 的直（8）求过点)1,2,1(-，并且平⾏直线线⽅程。

（9）求直线211232-+=-=+z y x 与平⾯08332=-++z y x 的交点和夹⾓。

（10）求点)0,2,1(-在平⾯012=+-+z y x 上的投影。

（11）求点)1,3,2(在直线322217+=+=+z y x 上的投影。

4201=-+-=+-+z y x z y x 的距离。

（12）求点)2,1,3(-P 到直线（13）求直线22x y z=??=?绕z 轴旋转⼀周的曲⾯⽅程并画出它的⼤致图形。

（14）求过直线026x y x y z +=??-+=?且切于球⾯2229x y z ++=的平⾯⽅程。

（15）设122112:,:112211x y z x y z L L -++-====--（1）判断12,L L 是否相交，若相交求出交点P 和相交平⾯π；（2）在平⾯π上求⼀过P 点直线L ，且L 与1L 和2L 的夹⾓相同。

⼆：（1）求1)sin(1lim)0,0(),(--→xy xy y x 。

一、判断题（本大题共10个小题，每小题2分，共20分）1．确定中学数学教学目的的依据是：教育的总目标、 、数学的学科特点、教师的状况、学生的年龄特征。

2．类比推理、归纳推理、演绎推理的推理方式依次是 、由个别到一般、由一般到个别。

3．中学数学思想方法的教学原则是目标性原则、 、概括性原则、实践性原则。

4．“说课”是中小学数学教学研究中普遍采用的形式，而且成为教学技能竞赛、考核和招聘教师的重要形式与方法。

说课的内容有 、教学方法、教学过程、教学注意点。

5．教师备课时，通过对教材的分析，要确定教学的重点、难点、关键，一般地把教材中贯穿全局、带动全面、起核心作用之点确定为教学的 。

6．义务教育数学课程标准的基本理念指出，学生是数学学习的主人，教师是数学学习的组织者、 、合作者。

7．启发式教学法，是教师遵循认知律，从学生的实际出发，在充分发挥教师主导作用的前提出下，善于激发学生的求知欲和学习兴趣，引导学生积极开展思维活动， 获取知识的一种教学方法。

8．．运算能力，是指不仅会根据法则、公式等正确地进行运算，而且理解 ，能够根据问题的条件寻求合理、简捷的运算途径。

9．基本数学活动经验，是指在 的指引下，通过对具体事物进行实际操作、考察和思考，从感性向理性飞跃时所形成的认识。

10．教学目标是选定课型和教学方法的依据，是检查教学效果的标尺，它包括认知目标、能力目标、 。

二、名词解释（本大题有3个小题，每小题5分，共15分）11．数学化12．数学双基教学13．数学教学模式三、简解答（本大题有3小题，每小题目10分，共30分）14．（本小题10分）20世纪数学教育观的变化数计系（本科）数学教育学重修试题注意事项：1、本试卷满分100分，共4页，答题时间为2小时。

2、答卷前将密封线内项目填写清楚。

15．（本小题10分）数学教学的原则16．（本小题10分）数学教学方案一般由哪几部分构成？.四、解答题（本大题共3个小题，共35分）17．（本小题11分）试谈谈数学教学中，如何培养学生的创造性18．（本小题12）自选一个中学数学概念，设计该概念教学的片断19．（本小题12分）谈谈你对新课标理念的认识。

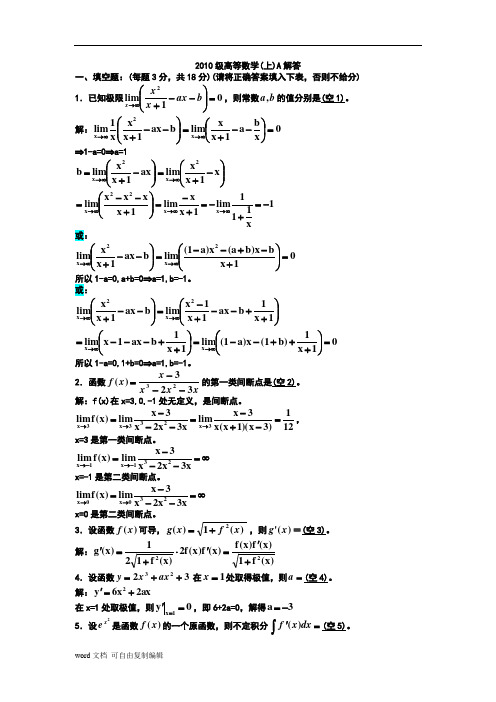
2010级高等数学(上)A 解答一、填空题：(每题3分，共18分)(请将正确答案填入下表，否则不给分)1．已知极限01lim 2=⎪⎪⎭⎫⎝⎛--+∞→b ax x x x ，则常数b a ,的值分别是(空1)。

解：0x b a 1x x lim b ax 1x x x 1lim x 2x =⎪⎭⎫ ⎝⎛--+=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ ⇒1-a=0⇒a=1⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=∞→∞→x 1x x lim ax 1x x lim b 2x 2x 1x111lim 1x x lim 1x x x x lim x x 22x -=+-=+-=⎪⎪⎭⎫ ⎝⎛+--=∞→∞→∞→ 或：01x b x )b a (x )a 1(lim b ax 1x x lim 2x 2x =⎪⎪⎭⎫⎝⎛+-+--=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ 所以1-a=0,a+b=0⇒a=1,b=-1。

或：⎪⎪⎭⎫⎝⎛++--+-=⎪⎪⎭⎫ ⎝⎛--+∞→∞→1x 1b ax 1x 1x lim b ax 1x x lim 2x 2x 01x 1)b 1(x )a 1(lim 1x 1b ax 1x lim x x =⎪⎭⎫ ⎝⎛+++--=⎪⎭⎫ ⎝⎛++---=∞→∞→ 所以1-a=0,1+b=0⇒a=1,b=-1。

2．函数xx x x x f 323)(23---=的第一类间断点是(空2)。

解：f(x)在x=3,0,-1处无定义，是间断点。

121)3x )(1x (x 3x lim x 3x 2x 3x lim)x (f lim 3x 233x 3x =-+-=---=→→→，x=3是第一类间断点。

∞=---=-→-→x3x 2x 3x lim)x (f lim 231x 1xx=-1是第二类间断点。

∞=---=→→x3x 2x 3x lim)x (f lim 230x 0xx=0是第二类间断点。

3．设函数)(x f 可导，)(1)(2x f x g +=，则)('x g ＝(空3)。

《高等数学》上册重修补考试卷（2010.12）一、填空：(20%)1.设)(x f 的定义域是[0，1]，则)(ln x f 的定义域为_________________。

2. n n n πsin lim ∞→=____________。

3. 已知)0(f '=1，)0(f =0，则xx f x )(lim 0→=________________。

4. 设函数⎩⎨⎧>+≤=,1,,1,)(2x b ax x x x f 在1=x 处连续且可导，则=a ________，=b ________。

5. 曲线xe y 2=在点（0,1）处的切线方程为_______________。

6. 设6)10()(+=x x f ，则)2(f '''=________。

7. x dt t x x ⎰→020cos lim =________。

8. 若21x是)(x f 的导数，则)(x f =_______________。

9. 曲线12++=x x y 在点（0,1）处的曲率为_______________。

二、计算下列各题：(48%) 1.)1(lim 2x x x x -++∞→ 2.x x x )arctan 2(lim π+∞→3. )1ln(2x x e e y ++=，求dy 。

4. 设⎩⎨⎧==ty t x 2cos sin 求dx dy ，22dx y d 。

5.dx xx x ⎰+4sin 1cos sin 6.dx x x ⎰ln ln 7.dx e x ⎰10 8.dx x ⎰-202sin 1π三、求函数3)1)(1()(+-=x x x f 的单调区间和极值。

(8%)四、证明：当1>x 时，ex e x >。

（8%）五、 求由曲线2x y =，2y x =所围成的图形绕x 轴旋转所得的旋转体的体积。

（8%）六、化工厂要造一个盛水300立方米的无盖圆柱形蓄水池，已知池底材料的单位造价为四周材料的单位造价的两倍，问怎样设计蓄水池尺寸，才能使造价最低？（8%）。

| | | | | | | |装 ||| | | 订|| || | |线| | | | | | | | | 防灾科技学院2009-2010学年第一学期检测考试答案及评分标准高等数学（一）试卷（A ）使用班级本科各专业 答题时间120分钟（本试卷理工、财经各专业通用，共三页23道题）一、单项选择题（本大题共15分，共计5小题，每小题3分。

）1. ()()()()f x f x f x -∞+∞--设是定义在，内的任意函数，则是 ；A.奇函数B.偶函数C.非奇非偶函数D.非负函数 2. 下列各对函数中，互为反函数的是 ；A. x y x y cos ,sin == B. x x e y e y -==C. x y x y cot tan ==D. 22x y x y ==3. 当+∞→x 时，下列变量为无穷小量的是 ；A. xB. )1l n (x +C. x s i nD. xe -4. 设0)0(=f ，且x x f x )(lim→存在，则xx f x )(lim 0→=；A. )0(fB. 0C. )0(/f D. )(/x f 5. =⋅⋅⋅⋅+-+∞→nn n n n n n n e e e e 121231lim 。

A.1 B. C.e D.2e二、填空题（本大题共15分，共计5小题，每小题3分） 6. 设)1ln(2)(x x x f -++=，则)(x f 的连续性区间为_______7. 设)0(2tan )(≠=x xxx f ，要使)(x f 在0=x 处连续，应补充定义=)0(f ； 8. =-+--→45215lim22x x x x ； 9.；若2)2(lim=→x f x x ，则x x f x )4(lim0→= 10.=++∞→xx x x 3)12(lim 。

三、计算极限(本大题共3小题，每小题5分，共计15分)11. xxx 5t a n ln 2tan ln lim 0→12. )12(lim 2n n n n --++∞→13. )1sin(lim 2n n n n -++∞→(本大题共4小题，每小题5分，共计20分)14.（5分） )(),()(ln(//22x y x y a a x x y '-+=是常数），求设　15.（5分） )(),(,1arctan )(//x y x y y y x x y y '=+-=求所确定由设　16. (5分) 设⎩⎨⎧+=+=ktt k y ktt k x cos cos sin sin （k 是非0常数）， 求022,=t dx y d dx dy17.(5分) 设32cos 1lnxxy +=，求dy五、 证明题(本大题共2小题，共计10分)18.（5分） 设)(x f 在开区间),(b a 内可导，且1)(lim )(lim ==-+→→x f x f bx ax 。

第1章 函数与极限1.用区间表达函数)4arcsin()3ln(-+-=x x xy 的自然定义域]5,4()4,3(⋃.解：应14,03,0)3ln(≤->-≠-x x x ，得141,3,13≤-≤->≠-x x x ，得]5,4()4,3(⋃. 3.已知1)1(2++=+x xxe ee f ,求)(x f 的表达式.解法1：因为1)1()1(1)1(22++-+=++=+x x x xxe e e ee f ，所以1)(2+-=x x x f .解法2：令1+=xe u ，则)1ln(-=u x ，代入式1)1(2++=+x xxe e ef ，得11)1()1(1)(22)1ln()1ln(2+-=+-+-=++=--u u u u e e u f u u ，即得1)(2+-=x x x f . 5.A x f x x =→)(lim 0的充分必要条件是A x f x f x x x x ==+-→→)(lim )(lim 0.6.=+→x x x 0lim 1 ,=-→x x x 0lim ―1 ,处的极限情况为 不存在 .解：在极限xx x +→0lim 中，+→0x ，此时0>x ，所以11lim lim lim 000===+++→→→x x x x x x x ， 在极限x x x -→0lim 中，-→0x ，此时0<x ，所以1)1(lim lim lim 000-=-=-=+--→→→x x x xx x x ， 因为A x f x x =→)(lim 0的充分必要条件是A x f x f x x x x ==+-→→)(lim )(lim 00，所以，xxx f =)(在0=x 处的极限xxx 0lim →不存在.1.若)(lim 0x f x x →存在,则)(x f B .A.有界;B.在),(0oδx U 内有界; C.在任一),(0δx U 内有界; D.以上结论都不对.解：A 选项不正确：因为函数极限存在时具有局部有界性，即保证函数在取极限的附近有界，在0x x →定点的情形，则是保证函数在0x 的去心邻域),(0oδx U 内有界； B 选项正确：即函数极限的局部有界性；C 选项不正确：应该是在某．一去心．．邻域内有界.2.设xe xf x1arctan )1()(1+=,当-→0x 时,观察)(x f 的变化趋势,可得=-)0(f C . A.0; B.2π; C.2π-; D.∞.解：)(lim )0(0x f f x -→-=，当-→0x 时，-∞→x 1，从而01→x e ，21arctan π-→x ，故2)2()01()(lim )0(0ππ-=-⋅+==-→-x f f x . 1.以下判断正确的是 D .A.xe 是无穷大量; B.x1是无穷小量; C.若当0x x →时,)(x f 是无穷小量,则)(1x f 是无穷大量; D.若A x f x x =→)(lim 0,则当0x x →时,A x f -)(是无穷小量.解：A 、B 选项都不正确：因为无穷大量及无穷小量都是针对自变量的一个变化过程而言的，但是A 、B 选项都没有给出自变量的变化过程.对于A 选项，例如，+∞=+∞→x x e lim ，因而xe是当+∞→x 时的无穷大量；又有1lim 0=→xx e ，因而当0→x 时xe 不是无穷大量. 对于B选项，例如，01lim =∞→x x ，因而x 1是当∞→x 时的无穷小量；又有∞=→xx 1lim 0，因而当0→x 时x1不是无穷小量，而是无穷大量. C 选项不正确：这是因为，如果0)(≡x f ，那么)(x f 对于自变量的任何变化过程而言都是无穷小量(当0x x →时亦然)，但是式)(1x f 无意义. D 选项正确：根据无穷小与函数极限的关系定理：在自变量的同一变化过程0x x →(∞→x )中,函数)(x f 具有极限A 的充分必要条件是α+=A x f )(,其中α是无穷小.2.试说明函数x x x f cos )(=在),(+∞-∞上无界,并说明)(x f 不是+∞→x 时的无穷大量.解：先说明函数x x x f cos )(=在),(+∞-∞上无界：因为对0>∀M ,在),(+∞-∞上总能找到这样的x ,使得M x f >)(.例如),2,1,0( 2)2cos(2)2( ±±===k k k k k f ππππ,当k 充分大时,就有M k f >)2(π.再说明函数)(x f 不是+∞→x 时的无穷大量：因为对0>∀M ,找不到这样的时刻X ,使得对于一切大于X 的x ,都有M x f >)(.例如),2,1,0( 0)22cos()22()22( ==++=+k k k k f ππππππ,对于任意大的X ,当k 充分大时,总有X k x >+=22ππ,但M x f <=0)(.1.01sin lim 0=→x x x 的理由是 有界函数x 1sin 与无穷小x 的乘积是无穷小 . 2.=-++→2232)2(2lim x x x x x ∞. 解：因为022220)2(lim )2(lim 2)2(lim 23232222322=+⋅+=++-=++-→→→x x x x x x x x x x x ，所以所求极限∞=-++→2232)2(2lim x x x x x . 3.=++-∞→503020)15()23()32(lim x x x x 503020532⋅. 解：所求极限是有理分式函数当∞→x 时的极限，并且分子、分母多项式的次数(x 的最高次)相同(均为50次)，则知极限值应为分子、分母x 的最高次的系数之比.因分子x 的最高次的系数是302032⋅,分母x 的最高次的系数是505,所以所求极限值是503020532⋅. 4.已知51lim21=-++→xcbx x x ,则=b ―7 ,=c 6 . 解：因为当1→x 时,分母)1(x -的极限为0,而分子)(2c bx x ++是多项式, 故当1→x 时,分子)(2c bx x ++的极限必存在,又已知51lim21=-++→xc bx x x 是有限值,所以分子)(2c bx x ++的极限应为0,即01)(lim 21=++=++→c b c bx x x ,得1--=b c .此时=--+-=---+=-++→→→x x b x x b bx x x c bx x x x x 1)1()1(lim 11lim 1lim 21212152)1(lim 1=--=---→b b x x ,得7-=b ,6=c .1.若}{n x 、}{n y 均发散,则下列判断正确的是 D .A.}{n n y x ±一定发散;B.}{n n y x ⋅一定发散;C.}{nny x 一定发散; D.以上结论都不对.解：A 、B 、C 选项都不正确，则D 选项正确：举例如1)1(,)1(+-=-=n n n n y x ，}{n x 及}{n y 均发散，但0=+n n y x 收敛.又例如n n n y x )1(-==，}{n x 及}{n y 均发散，但0=-n n y x 、1=⋅n n y x 及1=nny x 均收敛. 2.若}{n x 收敛,}{n y 发散,则下列判断正确的是 A . A.}{n n y x ±一定发散; B.}{n n y x ⋅一定发散; C.}{nny x 一定发散; D.以上结论都不对.解：A 选项正确(则D 选项不正确)，证明如下：设n n n y x z ±=，则n n n x z y ±=，用反证法，如果}{n z 收敛，则根据两函数和差的极限运算法则，有n n n n n n n n n x z x z y ∞→∞→∞→∞→±=±=lim lim )(lim lim ，即n y 收敛，此与}{n y 发散矛盾，故n n n y x z ±=一定发散. 证毕.B 、C 选项都不正确：举例如0=n x 收敛，nn y )1(-=发散，成立0==⋅nnn n y x y x 收敛. 5.)1311(lim 31xx x ---→; 解：11)2(lim )1)(1()2)(1(lim 13)1(lim )1311(lim 212132131-=+++-=++-+-=--++=---→→→→x x x x x x x x x x x x x x x x x . 6.xx x x +---→131lim 21;解：=++-+--++--=+---→→)13)(13()13)(1(lim 131lim 2121x x x x x x x x x x x x222)13)(1(lim )1(2)13)(1(lim 121-=++-+-=-++--=→→x x x x x x x x x . 7.)2141211(lim n n ++++∞→ ; 解：2211211lim)2141211(lim =--=++++∞→∞→nn n n . 8.)35(12721lim 2-++++-+∞→n n n n . 解：=--+=--+=-++++-+∑∑∑==∞→=∞→∞→n i n i n n i n n i n n i n n n n n 112122351lim )35(1lim )35(12721lim 5232)1(51lim 2=-+⋅-+∞→nn n n n n . 1.=→x xx ωsin lim 0ω. 解：ωωωωω=⋅=→→xx x x x x sin lim sin lim 00. 2.=-→x xx ππsin lim 1 . 解：1)sin(lim sin lim =--=-→→xx x x x x πππππ 3.=∞→n n n x 2sin 2lim x . 解：x x x x x nnn n n n =⋅=∞→∞→22sin lim2sin 2lim . 4.=+∞→nn n n 2)1(lim 2-e . 解：=+-+-=+---∞→∞→212)]111()111[(lim )1(lim nn n n n n n n 2221221)111(lim ])111[(lim )111(])111[(lim --∞→---∞→----∞→=+-⋅+-=+-+-=e nn n n n n n n n .或2221)11()11(1lim )/)1(/(lim )1(lim enn n n n n n n n n n n n n n =++=+=+∞→∞→∞→.5.若6)311(lim e x kxx =+-∞→,则=k ―6 .解：=+-+-=+-=+----∞→∞→∞→kx x k x x kx x x x x x ])311()311[(lim ])311[(lim )311(lim 336331])311(lim ])311[(lim e e x x k kx k x x =⋅=+-⋅+-=--∞→---∞→，得6-=k . 6.要使函数2tan )(x xx f =是无穷大,则要求x 趋于值),2,1(2 ±±=k k π.解：函数2tan )(x xx f =的定义域为}),,2,1,0({R x k k x x D ∈±±=≠= π.因为对任意点D x ∈0，根据两函数商的极限运算法则，必有)(2tan2tan lim)(lim 000x f x x x x x f x x x x ===→→是有限值，所以，使函数2tan )(x x x f =是无穷大的点只可能是不属于其定义域的点，即),2,1,0( ±±==k k x π.将这样的点分为3类，来求函数在该点处的极限：)()12(;0);,0(2Z k k x x Z k k k x ∈+==∈≠=ππ，求得)0(,02tanlim )(1lim 22≠==→→k xx x f k x k x ππ，所以)0(,)(lim 2≠∞=→k x f k x π；而22tan 2lim 22tan lim )(lim 000===→→→xxx xx f x x x ；02tan lim)(lim )12()12(==+→+→x x x f k x k x ππ)02sin 2coslim2tan 1lim()12()12(==+→+→x xx k x k x ππ；所以),2,1(2 ±±=k k π为所求.2.=-→x x x cos 1lim0 C . A.0; B.1; C.不存在; D.22.解：因为222sin2lim 2sin 2lim cos 1lim 0200===-+++→→→x x x x x x x x x ， 222sin2lim 2sin 2lim cos 1lim 0200-=-==-+--→→→x x x x x x x x x ， 左、右极限存在但不相等，所以该极限不存在，C 选项正确.1.]ln )1[ln(lim n n n n --∞→;解：1])11ln[(lim )11ln(lim 1lnlim ]ln )1[ln(lim 1-=-+=-=-=----∞→∞→∞→∞→n n n n n n nn n n n n n n . 2.)1cos arctan 1(lim 0x x x x x ⋅-→; 解：1011cos lim arctan lim )1cos arctan 1(lim 000=-=⋅-=⋅-→→→xx x x x x x x x x x . 3.xx x x 3)1212(lim -+∞→; 解：=-+=-+=-+∞→∞→∞→333])21211[(lim )1221(lim )1212(lim x x x x x x x x x x 2332122312)]21211(lim ])21211[(lim )]21211()21211[(lim -+⋅-+=-+⋅-+=∞→-∞→-∞→x x x x x x x x x 331e e =⋅=.4.x x x 4tan )21ln(lim 0+→; 解：212111214tan 42)21ln(lim 4tan )21ln(lim 00=⋅⋅=⋅⋅+=+→→x x x x x x x x . 四利用极限存在准则证明：1.1)1211(lim 222=++++++∞→πππn n n n n n .证明 因为)1211(222πππn n n n n ++++++ ππππ+=++++++≤22222)111(n n n n n n , 又)1211(222πππn n n n n ++++++ ππππn n n n n n n n n n +=++++++≥22222)111( , 而1lim 22=+∞→πn n n ,1lim 22=+∞→πn n n n ,由夹逼准则,得1)1211(lim 222=++++++∞→πππn n n n n n . 证毕. 1.当0→x 时,与x 等价的无穷小有aa x e x x x x x xln 1),1ln(,1,arctan ,arcsin ,tan ,sin -+-.解：根据等价无穷小的定义，只需逐一验证，1sin lim0=→x x x ，1tan lim 0=→x x x ，1arcsin lim 0=→xxx ，1arctan lim 0=→x x x ，11lim 0=-→x e x x ，1)1ln(lim 0=+→xx x ，1ln 1lim 0=-→x a a x x .2.设0→x ,则~cos 1x -22x ,~11-+n x nx.解：根据等价无穷小的定义，只需验证，12cos 1lim 20=-→xx x ，111lim 0=-+→n x x nx ：成立1)2(2sin lim 22sin 2lim 2cos 1lim 22022020===-→→→x xx x x x x x x . 成立=++++++-+=-+---→→])1()1()1([1)1(lim 11lim2100n nn n n n n n n x nx x x x nx x n x x (用到因式分解公式))((122321-----+++++-=-n n n n n n n b abb a b a a b a b a ) 11)1()1(lim 210==+++++=--→nnx x n n n nn x . (其中极限)1,,2,1(1)1(lim 0--==+→n n m x n mx 用到了习题1-6中题4(4)的结果11lim 0=+→n x x 及第五节中定理3的推论2)3.当0→x 时,22x x -与32x x -相比,哪一个是高阶无穷小?32x x -.解：根据高阶无穷小的定义，因为02)1(lim 2lim 02320=--=--→→xx x x x x x x x ，所以，分子32x x -是比分母22x x -高阶的无穷小.4.当1→x 时,无穷小x -1和31x -是否同阶? 同阶 ,是否等价? 不等价 .解：因为13111lim 11lim 2131≠=++=--→→x x x x x x ，所以无穷小x -1和31x -是同阶无穷小，但不是等价无穷小.1.当+→0x 时,下列哪一个无穷小是关于x 的三阶无穷小 B .A.x x -32; B.a x a -+3 (a 为正常数); C.230001.0x x +;D.3tan x .解：根据k阶无穷小的定义，A选项不正确：因为∞=+-+-=-+++→→→)(1lim )(lim lim 2132231021323340332x x x x x x x x x xxx x x x .B选项正确：因为=++=-+++→→)(lim lim 3330330a x a x x x a x a x x 0211lim 3≠=+++→aax a x .C 选项不正确：因为∞=+=+++→→)0001.01(lim 0001.0lim 03230xx x x x x . C 选项不正确：因为∞=⋅=++→→383303301tan lim tan lim x xx x x x x . 三利用等价无穷小的性质求下列极限：1.mn x x x )(sin )sin(lim 0→ (m n ,为正整数);解：m nx x x )(sin )sin(lim 0→⎪⎩⎪⎨⎧<∞=>==→.,,,1,,0lim 0m n m n m n x x mnx (m n ,为正整数).2.xx x x 30sin sin tan lim-→; 解：3030sin tan lim sin sin tan lim x x x x x x x x -=-→→21cos 2lim cos )cos 1(sin lim 32030=⋅=-=→→x x x x x x x x x x . 3.1)31ln(lim 2320--+→x x e x x ; 解：33lim 1)31ln(lim 23203202=-=--+→→x x x e x x x x x . 4.)1sin 1)(11(tan sin lim 320-+-+-→x x xx x .解：)1sin 1)(11(tan sin lim 320-+-+-→x x xx x 3tan sin lim 62sin 3tan sin lim 3020-=-=⋅-=→→x x x x x x x x x (利用2题结果或方法).1.设⎪⎪⎩⎪⎪⎨⎧>+<=,0,11sin ,0,sin 1)(x x x x x xx f 则0=x 是)(x f 的 A .A.可去间断点;B.跳跃间断点;C.无穷间断点;D.振荡间断点. 解：根据间断点的分类，考察：1sin 1lim )(lim )0(0===--→→-x xx f f x x ，1)11sin(lim )(lim )0(0=+==++→→+xx x f f x x ， 由于)0()0(+-=f f 即左右极限存在且相等，所以极限1)(lim 0=→x f x 存在，因而0=x 是)(x f 的可去间断点.故A 选项正确，B 、C 、D 选项不正确. 2.设11cotarc )(2-+=x x x f ,则1=x 是)(x f 的 B . A.可去间断点; B.跳跃间断点; C.无穷间断点; D.振荡间断点.解：根据间断点的分类，考察：π+=-+==--→→-1)11cot arc (lim )(lim )1(2110x x x f f x x ， 001)11cot arc (lim )(lim )1(2110=+=-+==++→→+x x x f f x x ，由于左右极限存在但不相等，所以1=x 是)(x f 的跳跃间断点.故B 选项正确，A 、C 、D 选项不正确. 3.设xee xf xx1arctan121)(11+-=,则0=x 是)(x f 的 B . A.可去间断点; B.跳跃间断点; C.无穷间断点; D.振荡间断点.解：注意到∞==+-→→xx xx e e 1010lim ,0lim ，21arctan lim ,21arctanlim 00ππ=-=+-→→x x x x . 根据间断点的分类，考察：2)2(11arctan121lim )(lim )0(11ππ-=-⋅=+-==--→→-x ee xf f x xx x , ππ-=⋅-=+-==++→→+221arctan121lim )(lim )0(110x ee xf f xxx x ，由于左右极限存在但不相等，所以0=x 是)(x f 的跳跃间断点.故B 选项正确，A 、C 、D 选项不正确.1.下列函数在指出的点处间断,说明这些间断点属于哪一类.如果是可去间断点,则补充或改变函数的定义使它连续:(1)2,1,23122==+--=x x x x x y ; 解：1 2231lim 221=∴-=+--→x x x x x 为第一类(可去)间断点.补充定义,2)1(-=y 则函数y 在1=x 处连续.2 231lim 222=∴∞=+--→x x x x x 为第二类(无穷)间断点. (2) 2,,tan πππ+===k x k x x x y ( ,2,1,0±±=k );解： 0 1tan lim 0=∴=→x xxx 为可去间断点.补充定义,1)0(=y 则函数y 在0=x 处连续.2 0tan lim 2ππππ+=∴=+→k x xx k x 为可去间断点.补充定义,0)2(=+ππk y 则函数y在2ππ+=k x 处连续.)0( )0(tan lim≠=∴≠∞=→k k x k x xk x ππ 为第二类(无穷)间断点.(3)0,1cos 2==x x y . 解：因为x x 1cos lim 20-→(或xx 1cos lim 20+→)不存在，所以0=x 为第二类间断点(且为振荡间断点).1.函数633)(223-+--+=x x x x x x f 的连续区间为),2(),2,3(),3,(+∞---∞,极限=→)(lim 0x f x 21,=-→)(lim 3x f x 58-,=→)(lim 2x f x ∞.解：在此633)(223-+--+=x x x x x x f 是有理分式函数，根据有理分式函数在其定义区域内的每一点都是连续的，又此函数定义区域为),2(),2,3(),3,(+∞---∞，可知)(x f 的连续区间即)(x f 的定义域为),2(),2,3(),3,(+∞---∞.又根据函数间断点的概念，可知函数)(x f 没有定义的点2,3=-x x 是其间断点.因为0=x 是连续点，所以极限21)0()(lim 0==→f x f x ；而在间断点2,3=-x x 处，极限5821lim )3)(2()3)(1(lim 633lim )(lim 232322333-=--=+-+-=-+--+=-→-→-→-→x x x x x x x x x x x x f x x x x ；极限∞=-+--+=→→633lim )(lim 22322x x x x x x f x x . 4.设函数⎩⎨⎧≥+<=,0,,0,)(x x a x e x f x 若要使)(x f 成为在),(+∞-∞上连续的函数,应当选择=a1 .解：若要使)(x f 在),(+∞-∞上连续，那么)(x f 必在其分段点0=x 处连续，即成立)0()(lim 0f x f x =→，则必有)(lim )(lim 0x f x f x x +-→→=.而1lim )(lim 0==--→→x x x e x f ，a x a x f x x =+=++→→)(lim )(lim 00，故1=a ，此时)0(1)(lim 0f a x f x ===→.二求下列极限：3.145lim 1---→x x x x ; 解：2)45)(1()1(4lim 145lim 11=+---=---→→x x x x x x x x x .4.ax ax a x --→sin sin lim; 解：a a x a x a x a x a x a x a x a x a x a x a x cos 2cos 22sinlim 2sin 2cos 2lim sin sin lim =+⋅--=--+=--→→→. 5.)(lim 22x x x x x --++∞→. 解：111112lim2lim)(lim 2222=-++=-++=--++∞→+∞→+∞→xx xx x x x x x x x x x x .三求下列极限：1.xx e 1lim ∞→; 解：1lim 1=∞→x x e .2.x xx sin lnlim 0→; 解：0sin lnlim 0=→xx x . 3.)arcsin(lim 2x x x x -++∞→. 解：621arcsinarcsinlim )arcsin(lim 22π==++=-++∞→+∞→xx x x x x x x x . 一证明题1.证明方程135=-x x 至少有一个根介于1和2之间. 证明 设13)(5--=x x x f ，对)(x f 在闭区间[1,2]上用零点定理：因为13)(5--=x x x f 在闭区间[1,2]上连续，并且0)72()3()2()1(5<-⋅-=⋅f f ，所以由零点定理可得，至少存在一点)2,1(∈ξ使0)(=ξf ，即0135=--ξξ，亦即方程135=-x x 至少有一个根介于1和2之间. 证毕.2.证明方程b x a x +=sin ,其中0,0>>b a ,至少有一个正根,并且它不超过b a +. 证明 思路如下：先构造辅助函数)sin ()(b x a x x F +-=，则方程b x a x +=sin 的根的问题即转化为函数)(x F 的零点的问题；然后判断)(x F 在某闭区间上连续且在端点处的函数值异号，于是根据闭区间上连续函数的零点定理即可断定)(x F 的零点亦即方程根的存在性；本题欲证方程的根为正根，并且它不超过b a +，故在闭区间],0[b a +上进行考察.令)sin ()(b x a x x F +-=，则0)0(<-=b F ,=+)(b a F 0)]sin(1[≥+-b a a ，以下分两种情况讨论：①当1)sin(=+b a ，0)(=+b a F ，则b a +就是函数)(x F 的零点，也就是方程b x a x +=sin 的一个根，此根],0(b a b a +∈+，取到区间],0(b a +的右端点；②当1)sin(<+b a ，0)(>+b a F ，因为)(x F 在(∞∞-,)上连续, 从而在],0[b a +上连续，并且0)()0(<+⋅b a F F ，于是根据闭区间上连续函数的零点定理可得，在开区间),0(b a +内至少存在一点ξ，使0)(=ξF ，即ξ是方程b x a x +=sin 的一个根，此根),0(b a +∈ξ.由①②即得，方程b x a x +=sin 在],0(b a +内至少有一个根. 证毕. 4.若在0x 的某个邻域内)()(x x f ϕ>,且A x f x x =→)(lim 0,B x x x =→)(lim 0ϕ,则A 与B 的关系是B A ≥.解：根据函数极限的性质定理：如果)()(x x ψϕ≥，而b x a x ==)(lim ,)(lim ψϕ，那么b a ≥.(第五节定理5)5.设)(x f 处处连续,且5)2(=f ,则=-→)1(3tan lim20xe f x x x x 15 . 解：注意到)(x f 处处连续，则15)2(3)212(33tan 3lim )1(3tan lim 2020=⋅=-⋅⋅=-→→f xe f x x x e f x x x x x x . 2.设232)(-+=xx x f ,则当0→x 时,以下四个结论中正确的结论是 B .A.)(x f 与x 是等价无穷小;B.)(x f 与x 同阶但非等价无穷小;C.)(x f 是比x 高阶的无穷小;D.)(x f 是比x 低阶的无穷小.解：根据无穷小比较的定义，因为6ln 3ln 2ln )13()12(lim 232lim )(lim 000=+=-+-=-+=→→→xx x x f x x x x x x x ， 由16ln ≠知A 选项不正确，由06ln ≠知B 选项正确且C 选项不正确，由6ln 非∞知D选项不正确.三求下列极限：1.])12)(12(1751531311[lim +-++⋅+⋅+⋅∞→n n n .解：])12)(12(1751531311[lim +-++⋅+⋅+⋅∞→n n n )]121121()7151()5131()3111[(21lim +--++-+-+-=∞→n n n 21)1211(lim 21=+-=∞→n n .2.)11()311)(211(lim 222nn ---∞→ . 解：)11()311)(211(lim 222nn ---∞→ ))1)(1(111(2222n n n n n n --=-=- 2222)1)(1(453342231lim n n n n --⋅⋅⋅⋅⋅=∞→ 2121lim =+=∞→n n n . 3.)tan 1sin 1(1lim 0x x x x -→. 解：)tan 1sin 1(1lim 0x x x x -→2121lim sin cos 11lim 2200==-⋅=→→x x x x x x x .4.x x x x x 1sin ln 1cos ln lim 0+++→. 解：x x x x x 1sin ln 1cos ln lim 0+++→11sinln 111cosln 11lim 0=++=+→xx x x x . 5.ππ-∞→3232sinlimx x x x x . 解：ππ-∞→3232sinlimx x x x x πππππ=-=-⋅=∞→∞→333232limlimx x x x x x x x . 6.)111)(110()110()12()1(lim222--++++++∞→x x x x x x . 解：)111)(110()110()12()1(lim222--++++++∞→x x x x x x 271110102122=⋅+++= . 7.)0,0,0.()3(lim 10>>>++→c b a c b a xx x x x . 解：xx x x x c b a 10)3(lim ++→xx x x x c b a 10)331(lim -+++=→313330)331(lim ⋅-++⋅-++→-+++=x c b a c b a xxxx x x x x x x c b a ， )111(lim 3lim 00xc x b x a x c b a x x x x x x x x -+-+-=-++→→ abc c b a ln ln ln ln =++=，所以原式abc e ln 31=3abc =.8.x x x cot 0)]4[tan(lim -→π. 解：x x x cot 0)]4[tan(lim -→π2tan 11tan 10)tan 1(])tan 1[(lim---→=+-=e x x xx x .9.xx x tan 2)(sin lim π→.解：xx x tan 2)(sin lim π→xx x x cos sin 2)]1(sin 1[lim -+=→πxxx x x x sin cos 1sin 1sin 12)]1(sin 1[lim ⋅-⋅-→-+=π，x x x x x x x cos 1sin lim sin cos 1sin lim 22-=⋅-→→ππ 02sin 2cos 2cos 2sin lim 2sin 2cos )2cos 2(sin lim22222=+-=---=→→x x x x x x x x x x ππ，所以原式10==e .10.1111lim 30-+-+→x x x . 解：1111lim 30-+-+→x x x )11)(11)1()(11()11)1()(11)(11(lim33233320++++++-+++++++-+=→x x x x x x x x x 23)11()11)1((lim 3320=++++++=→x x x x x x . 11.xx x x x x sin 114lim 22+++-+-∞→.解：xx x x x x sin 114lim22+++-+-∞→xx x x x x x x -+-++-+=-∞→sin 114lim221sin 111114lim2=+---+=-∞→xx x x x x .12.)0( .1lim>+∞→a a an nn 解：)0( .1,1,1,21,100,1lim >⎪⎩⎪⎨⎧>=<<=+∞→a a a a a a n nn 2.设函数⎪⎪⎩⎪⎪⎨⎧≤->++=,0,cos ,0,)1ln(1cos sin )(2x x be x x x x x x f x应当怎样选择数b ,使得)(x f 在0=x 处连续. 解：应有)0()(lim )(lim 0f x f x f x x ==-+→→,而1)0()(lim ,1)(lim 00-===-+→→b f x f x f x x ,所以2=b .3.设函数⎪⎩⎪⎨⎧≤<-+>=-,01),1ln(,0,)(11x x x e x f x 求的间断点,并说明间断点所属类型. 解：因为函数在1=x 处无定义(在)1(0U 有定义),所以1=x 是)(x f 的一个间断点.)11lim ( 0lim )(lim 11111-∞=-==---→-→→x ex f x x x x ,)11lim ( lim )(lim 11111+∞=-∞==+++→-→→x ex f x x x x , 1=∴x 是第二类间断点.在分段点0=x 处,eex f x x f x x x x x 1lim )(lim ,0)1ln(lim )(lim 110===+=-→→→→++-- , 0=∴x 也是)(x f 的间断点,且是第一类间断点. 五证明题2.设函数)(x f 在闭区间],[b a 上连续,且b b f a a f ><)(,)(,证明:在),(b a 内至少存在一点ξ,使ξξ=)(f .证明 设x x f x g -=)()(,对)(x g 在闭区间],[b a 上用零点定理:由)(x f 在闭区间],[b a 上连续,可得x x f x g -=)()(在闭区间],[b a 上连续,并且0)()(<-=a a f a g ,0)()(>-=b b f b g ,故由零点定理得,在),(b a 内至少存在一点ξ,使0)()(=-=ξξξf g ,即ξξ=)(f . 证毕.3.设函数)(x f 在),(b a 内连续,),(0b a x ∈,且0)(0>=A x f .证明:存在0x 的邻域),(),(0b a x U ⊂δ,使当x 属于该邻域时,A x f 21)(>.证明 设2)()(A x f x g -=,则022)(]2)([lim )(lim 000>=-=-=→→AA x f A x f x g x x x x ,由极限的局部保号性知,存在00>δ,使当000δ<-<x x 时,有0)(>x g .取},,m in{000x b a x --=δδ,则当),(),(0b a x U x ⊂∈δ时,有0)(>x g ,即A x f 21)(>. 毕.友情提示：范文可能无法思考和涵盖全面，供参考!最好找专业人士起草或审核后使用，感谢您的下载！。

本科高数重修试题及答案一、单项选择题（每题3分，共30分）1. 函数f(x)=x^2-4x+3的零点个数是（）。

A. 0B. 1C. 2D. 32. 极限lim(x→0) (x^2-1)/(x^2+1)的值是（）。

A. 0B. 1C. -1D. 23. 函数f(x)=e^x-x-1的导数是（）。

A. e^x-1C. e^x-xD. e^x+x4. 函数f(x)=x^3+3x^2+3x+1的极值点是（）。

A. x=-1B. x=-2C. x=-3D. x=15. 曲线y=x^2+2x+1在点(1,4)处的切线斜率是（）。

A. 2B. 3C. 4D. 56. 函数f(x)=x^3-3x^2+2x的拐点是（）。

A. x=1C. x=3D. x=07. 函数f(x)=x^2-4x+4的最小值是（）。

A. 0B. 4C. -4D. 88. 函数f(x)=x^3-3x^2+2x的单调递增区间是（）。

A. (-∞, 1)B. (1, 2)C. (2, +∞)D. (-∞, 2)9. 曲线y=x^2+2x+1与直线y=4相切的切点坐标是（）。

A. (1, 4)C. (2, 4)D. (-2, 4)10. 函数f(x)=x^3-3x^2+2x的不定积分是（）。

A. (1/4)x^4-x^3+x^2+CB. (1/3)x^3-x^2+2x+CC. (1/4)x^4-x^3+2x^2+CD. (1/3)x^3-x^2+x+C二、填空题（每题4分，共20分）11. 函数f(x)=x^2-4x+3的零点是_________。

12. 极限lim(x→0) (x^2-1)/(x^2+1)的值是_________。

13. 函数f(x)=e^x-x-1的导数是_________。

14. 函数f(x)=x^3+3x^2+3x+1的极值点是_________。

15. 曲线y=x^2+2x+1在点(1,4)处的切线斜率是_________。

高数大一习题2-1答案高数（高等数学）是大学一年级的必修课程之一，对于很多学生来说，高数是一门难以逾越的学科。

而习题是学习高数的重要环节，通过解答习题可以巩固知识，提高解题能力。

本文将为大家提供高数大一习题2-1的答案，希望能对大家的学习有所帮助。

2-1习题是高数中的基础部分，主要涉及到函数的概念、性质和运算。

下面将逐题进行解答。

1. 设函数f(x) = 2x + 3，求f(1)的值。

解答：将x = 1代入函数f(x)中，得到f(1) = 2(1) + 3 = 5。

所以f(1)的值为5。

2. 设函数f(x) = x^2 - 4x + 3，求f(-1)的值。

解答：将x = -1代入函数f(x)中，得到f(-1) = (-1)^2 - 4(-1) + 3 = 1 + 4 + 3 = 8。

所以f(-1)的值为8。

3. 设函数f(x) = 3x^2 + 2x - 1，求f(2)的值。

解答：将x = 2代入函数f(x)中，得到f(2) = 3(2)^2 + 2(2) - 1 = 12 + 4 - 1 = 15。

所以f(2)的值为15。

4. 设函数f(x) = x^3 - x，求f(0)的值。

解答：将x = 0代入函数f(x)中，得到f(0) = (0)^3 - 0 = 0。

所以f(0)的值为0。

5. 设函数f(x) = 2x^2 + 3x + 1，求f(-2)的值。

解答：将x = -2代入函数f(x)中，得到f(-2) = 2(-2)^2 + 3(-2) + 1 = 8 - 6 + 1 = 3。

所以f(-2)的值为3。

6. 设函数f(x) = x^2 + 2x + 1，求f(3)的值。

解答：将x = 3代入函数f(x)中，得到f(3) = (3)^2 + 2(3) + 1 = 9 + 6 + 1 = 16。

所以f(3)的值为16。

通过以上六道题目的解答，我们可以看到，求函数在某一点的值，只需要将该点的横坐标代入函数中，进行计算即可。