下载文档原格式
第五节 强度理论一、强度理论概述各种材料因强度不足而引起的失效现象是不同的。
根据第五章的讨论，我们知道象普通碳钢这样的塑性材料，是以发生屈服现象、出现塑性变形为失效的标志；而象铸铁这样的脆性材料，失效现象是突然断裂。
第五～八章的强度条件可以概括为最大工作应力不超过许用应力，即[]σ≤σmax 或[]τ≤τmax 。
这里的许用应力是从试验测得的极限应力除以安全系数得到的，这种直接根据试验结果来建立强度条件的方法，对于危险点处于复杂应力状态的情况不再适用。
这是因为复杂应力状态下三个主应力的组合是各种各样的，1σ、2σ和3σ之间的比值有无限多种情形，不可能对所以的组合都一一试验确定其相应的极限应力。
事实上，尽管失效现象比较复杂，但可以归纳为如下二点：1．材料在外力作用下的破坏形式不外乎有几种类型；2．同一类型材料的破坏是由某一个共同因素引起的。
人们在长期的实践中，综合多种材料的失效现象和资料，对强度失效提出各种假说。
这些假说认为，材料按断裂或屈服失效，是应力、应变或变形能等其中某一因素引起的。
按照这些假说，无论是简单还是复杂应力状态，引起失效的因素是相同的，造成失效的原因与应力状态无关。
这些假说称为强度理论。
利用强度理论，就可以利用简单应力状态下的试验（例如拉伸试验）结果，来推断材料在复杂应力状态下的强度，建立复杂应力状态的强度条件。
强度理论是推测材料强度失效原因的一些假说，它的正确与否以及适用范围，必须在工程实践中加以检验。
经常是适用于某类材料的强度理论，并不适用于另一类材料。
下面介绍的四种强度理论，都是在常温静载荷下，适用于均匀、连续、各向同性材料的强度理论。
二、四种强度理论1） 最大拉应力理论（第一强度理论）这一理论认为引起材料脆性断裂破坏的因素是最大拉压力，它是人们根据早期使用的脆性材料（象天然石、砖和铸铁等）易于拉断而提出的。
该理论认为无论什么应力状态下，只要构件内一点处的最大拉压力1σ达到单向应力状态下的极限应力b σ，材料就要发生脆性断裂。
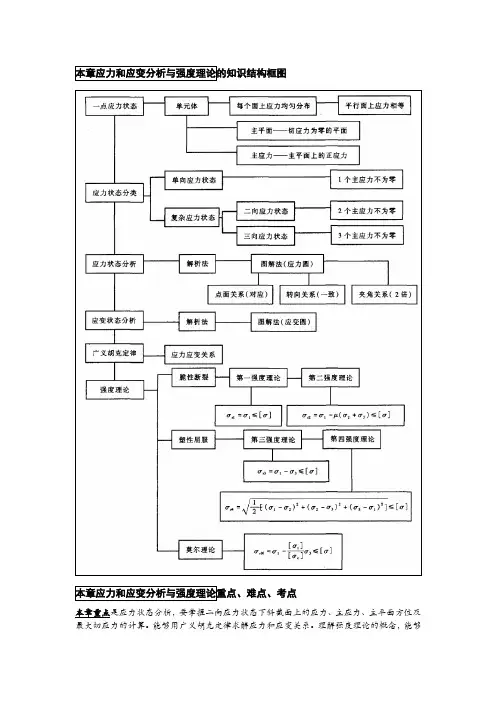
本章应力和应变分析与强度理论的知识结构框图本章应力和应变分析与强度理论重点、难点、考点本章重点是应力状态分析，要掌握二向应力状态下斜截面上的应力、主应力、主平面方位及最大切应力的计算。
能够用广义胡克定律求解应力和应变关系。
理解强度理论的概念，能够按材料可能发生的破坏形式，选择适当的强度理论。
难点主要有 ① 主平面方位的判断。
当由解析法求主平面方位时，结果有两个相差 90 ”的方位角，一般不容易直接判断出它们分别对应哪一个主应力，除去直接将两个方位角代人式中验算确定的方法外，最简明直观的方法是利用应力圆判定，即使用应力圆草图。
还可约定y x σσ≥，则两个方位中绝对值较小的角度对应max σ所在平面。
② 最大切应力。
无论何种应力状态，最大切应力均为2/)(31max σστ-=，而由式（ 7 一 l ）中第二式取导数0d d =ατα得到的切应力只是单元体的极值切应力，也称为面内最大切应力，它仅对垂直于Oxy 坐标平面的方向而言。
面内最大切应力不一定是一点的所有方位面中切应力的最大值，在解题时要特别注意，不要掉人“陷阱”中。
本章主要考点： ① 建立一点应力状态的概念，能够准确地从构件中截取单元体。
② 二向应力状态下求解主应力、主平面方位，并会用主单元体表示。
会计算任意斜截面上的应力分量。
③ 计算单元体的最大切应力。
④ 广义胡克定律的应用。
⑤ 能够选择适当的强度理论进行复杂应力状态下的强度计算，会分析简单强度破坏问题的原因。
本章应力和应变分析与强度理论的习题分类及解题要点：本章习题大致可分为四类：( l ）从构件中截取单元体这类题一般沿构件截面截取一正六面体，根据轴力、弯矩判断横截面上的正应力方向，由扭矩、剪力判断切应力方向，单元体其他侧面上的应力分量由力平衡和切应力互等定理画完整。
特别是当单元体包括构件表面（自由面）时，其上应力分量为零。
( 2 ）复杂应力状态分析一般考题都不限制采用哪一种方法解题，故最好采用应力圆分析，它常常能快速而有效地解决一些复杂的问题。
