22.1.3二次函数的图象和性质(4)
- 格式:doc
- 大小:107.00 KB
- 文档页数:6

人教版九年级数学上册22.1.3《二次函数的图象和性质》比赛说课稿一. 教材分析《二次函数的图象和性质》是人教版九年级数学上册第22.1.3节的内容。
本节主要介绍二次函数的图象和性质,是学生在学习了二次函数的定义、标准式、顶点式的基础上进行的。
通过本节的学习,使学生掌握二次函数的图象特征,了解二次函数的增减性、对称性、周期性等性质,为学生进一步解决实际问题打下基础。
二. 学情分析九年级的学生已经具备了一定的数学基础,对二次函数的基本概念和性质有所了解。
但学生在学习过程中,对二次函数的图象和性质的理解还不够深入,尤其对一些概念的内涵和外延认识不清晰。
因此,在教学过程中,要注重引导学生从直观的图象中感知二次函数的性质,让学生在动手实践、合作交流中理解知识,提高学生的数学思维能力。
三. 说教学目标1.知识与技能目标:让学生掌握二次函数的图象特征,了解二次函数的增减性、对称性、周期性等性质。
2.过程与方法目标:通过观察、分析、归纳等方法,让学生从图象中感知二次函数的性质,提高学生的数学观察能力和逻辑思维能力。
3.情感态度与价值观目标:培养学生对数学的兴趣,激发学生探究数学问题的热情,培养学生的团队协作精神。
四. 说教学重难点1.教学重点:二次函数的图象特征,二次函数的增减性、对称性、周期性等性质。
2.教学难点:二次函数性质的灵活运用,对一些特殊函数图象的理解。
五. 说教学方法与手段1.教学方法:采用“引导发现法”、“案例教学法”和“合作学习法”。
2.教学手段:利用多媒体课件、黑板、粉笔等传统教学手段,结合学习卡、练习题等辅助教学手段。
六. 说教学过程1.导入新课:通过展示一些实际问题,引导学生关注二次函数的图象和性质,激发学生的学习兴趣。
2.知识讲解:讲解二次函数的图象特征,引导学生从图象中感知二次函数的性质。
通过典型案例,使学生了解二次函数的增减性、对称性、周期性等性质。
3.课堂练习:设计一些具有针对性的练习题,让学生在实践中巩固所学知识。



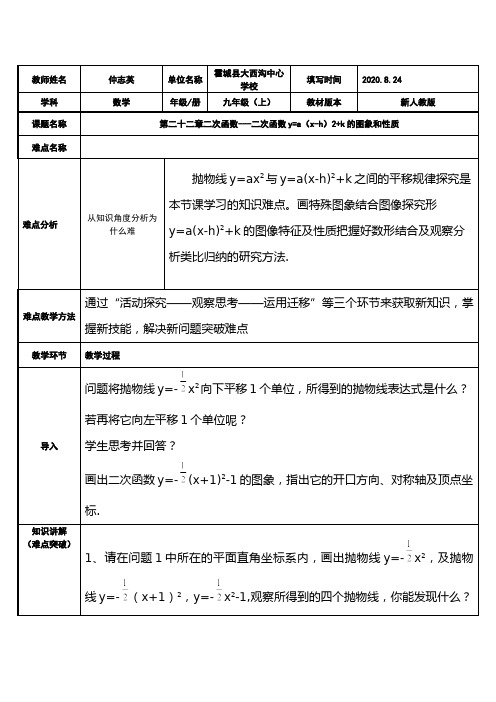
教师姓名仲志英单位名称霍城县大西沟中心学校填写时间2020.8.24学科数学年级/册九年级(上)教材版本新人教版课题名称第二十二章二次函数---二次函数y=a(x-h)2+k的图象和性质难点名称难点分析从知识角度分析为什么难抛物线y=ax2与y=a(x-h)2+k之间的平移规律探究是本节课学习的知识难点。
画特殊图象结合图像探究形y=a(x-h)2+k的图像特征及性质把握好数形结合及观察分析类比归纳的研究方法.难点教学方法通过“活动探究——观察思考——运用迁移”等三个环节来获取新知识,掌握新技能,解决新问题突破难点教学环节教学过程导入问题将抛物线y=-x2向下平移1个单位,所得到的抛物线表达式是什么?若再将它向左平移1个单位呢?学生思考并回答?画出二次函数y=-(x+1)2-1的图象,指出它的开口方向、对称轴及顶点坐标.知识讲解(难点突破)1、请在问题1中所在的平面直角坐标系内,画出抛物线y=-x2,及抛物线y=-(x+1)2,y=-x2-1,观察所得到的四个抛物线,你能发现什么?问题2、请依据问题2中你的发现,说说抛物线y=a(x-h)2+k是由抛物线y=ax2(a≠0)通过怎样的平移而得到的?并说说它的对称轴和顶点坐标.【设计意图】教师可给予15~20分钟的时间让学生自主探究,画出图象,并让学生们交流,获得感性认识.教师巡视,鼓励每个学生积极参与进来,针对个别同学,应适时予以点拨.如果条件允许,对学生的成果可通过多媒体展示.2、精讲点拨:1.一般地,抛物线y=a(x-h)2+k与抛物线y=ax2的形状相同(因为a 值相同),而位置不同.将抛物线y=ax2上下平移,可得到抛物线y=ax2+k(k>0时,向上平移k个单位;k<0时,向下平移-k个单位),再将抛物线y=ax2+k左右平移后,可得到抛物线y=a(x-h)2+k(h>0时,向右平移;h<0时,向左平移).(简称:上加下减函数值,左加右减自变量。

第二十二章 22.1.3二次函数y=ax2+k的图象和性质知识点:二次函数y=ax2+k的图象及其性质二次函数y=ax2+k的性质与二次函数y=ax2的性质很多都相同,只是图象顶点坐标及最值有所区别,但也可以由二次函数y=ax2的图象的顶点平移得到二次函数y=a x2+k的图象的顶点的坐标,因而学习二次函数y=ax2+k的性质,可在熟记二次函数y=ax2的性质的基础上类比学习.二次函数图象开口方向顶点坐标对称轴增减性最大(小)值y=ax2+ka>0k>0向上(0,k)y轴当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小当x=0时,y最小值=ka>0k<0向上(0,k)y轴当x>0时,y随x的增大而增大;当x<0时,y随x的增大而减小当x=0时,y最小值=k a<0k>0向下(0,k)y轴当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大当x=0时,y最大值=k a<0k<0向下(0,k)y轴当x>0时,y随x的增大而减小;当x<0时,y随x的增大而增大当x=0时,y最大值=k 二次函数的解析式中常数项的变化与其图象移动的关系:上加下减.考点1:二次函数y=ax2+k的图象【例1】小明在某次投篮中,球的运动路线是抛物线y=-x2+3.5的一部分(如图),若投中篮框中心,则他与篮底的距离l是( )A.3.5 mB.4 mC.4.5 mD.4.6 m答案:B点拨:由题意令y=3.05,可得3.05=-x2+3.5,解得x=±1.5(负值不符合题意,舍去),所以他与篮底的距离l=1.5+2.5=4(m).考点2:二次函数y=ax2+k的性质【例2】将抛物线y=-3x2向上平移1个单位后,得到的抛物线对应的函数解析式是.答案:y=-3x2+1点拨:由“上加下减”的规律知,该抛物线向上平移1个单位后得到的抛物线对应的函数解析式为y=-3x2+1.感谢您的支持,我们会努力把内容做得更好!。
先列表:
x … 3 4 5 6 7 8 9 …
y =2
1(x -6)2
+3
… 7.5 5
3.5
3
3.5 5 7.5 …
然后描点画图,得到y =2
1(x -6)2+3的图象. 从上图中二次函数的图象可以看出: 抛物线y =2
1
x 2-6 x +21的顶点是(6,
3),对称轴是x =6.在对称轴的左侧,抛物线从左到右下降;在对称轴的右侧,抛物线从左到右上升.也就是说,当x <6时,y 随x 的增大而减小;当x >6时,y 随x 的增大而增大.
2.用上面的方法讨论二次函数y =-2x 2-4 x +1的图象和性质. 教师引导学生独立完成,教师在学生配方时可给予适当指导.
y =-2x 2-4 x +1
=-2(x 2+2 x -2
1) =-2(x 2+2 x +1-1-2
1) =-2[(x +1)2-2
3] =-2(x +1)2+3.
三,探究新知
【师生互动】教师组织学生分组讨论,各组选派代表发言,全班交流,达成共识;
以上讲的,都是给出一个具体的二次函数,来研究它的图象与性质。
那么,对于任意一个二次函数y =ax 2+bx +c(a ≠0),如何确定它的图象的开口方向、对称轴和顶点坐标?你能把结果写出来吗? y =ax 2+bx +c =a(x 2+b a x)+c =a[x 2+b a x +(b 2a )2-(b
2a
)2]+c。