二次函数的图像与性质知识点及练习

二次函数的图象与性质专题【知识点1 二次函数的配方法】二次函数y =ax 2+bx +c (a ≠0)配方成顶点式y =a (x +b 2a )2+4ac−b 24a 2， 对称轴为2b x a =−，顶点坐标为2424b ac b a a ⎛⎫−− ⎪⎝⎭，．【题型1 二次函数的配方法】【例1】用配方法将下列函数化成y ＝a （x -h ）2+k 的形式，并指出抛物线的开口方向，对称轴和顶点坐标．（1）y ＝2x 2+4x -1 （2）y =12x 2﹣2x +3； （3）y ＝（1﹣x ）（1+2x ）；【知识点2 二次函数的五点绘图法】利用配方法将二次函数2y ax bx c =++化为顶点式2()y a x h k =−+，确定其开口方向、对称轴及顶点坐标，然后在对称轴两侧，左右对称地描点画图.一般我们选取的五点为：顶点、与y 轴的交点()0c ，、以及()0c ，关于对称轴对称的点()2h c ，、与x 轴的交点()10x ，，()20x ，（若与x 轴没有交点，则取两组关于对称轴对称的点）. 画草图时应抓住以下几点：开口方向，对称轴，顶点，与x 轴的交点，与y 轴的交点.【题型2 二次函数的五点绘图法】【例2】已知抛物线y ＝x 2﹣2x ﹣3（1）写出该抛物线的开口方向、顶点坐标、对称轴、与x 、y 轴交点；（2）选取适当的数据填表格，并在直角坐标系内描点画出该抛物线的图象．【知识点3 二次函数的图象与各系数之间的关系】①二次项系数a ：a 决定了抛物线开口的大小和方向，a 的正负决定开口方向，a 的大小决定开口的大小． ②一次项系数b ：在a 确定的前提下，b 决定了抛物线对称轴的位置，概括的说就是“左同右异”. ③常数项c ：总结起来，c 决定了抛物线与y 轴交点的位置．【题型3 二次函数的图象与各系数之间的关系】【例3-1】如图所示的四个二次函数图象分别对应 ①y =ax 2， ②y =bx 2， ③y =cx 2， ④y =dx 2，则a ，b ，c ，d 的大小关系为 .(用“>”连接)【例3-2】二次函数y=ax2+bx+c（a≠0）图像如图，下列结论：①abc>0；②2a+b=0；③当m≠1时，a+b>am2+bm；④a-b+c>0；⑤若ax12+bx1=ax22+bx2，且x1≠x2，x1+x2=2．其中正确的有（）A．②④B．②⑤C．①②③D．②③⑤【例3-3】函数y＝ax2﹣a与y＝ax+a（a≠0）在同一坐标系中的图象可能是（）A．B．C．D．【知识点4 二次函数图象的平移变换】平移步骤：①将抛物线解析式转化成顶点式()2y a x h k=−+，确定其顶点坐标()h k，；②平移规律概括成八个字“左加右减，上加下减”．【题型4 二次函数图象的平移变换】【例4】要得到函数y＝﹣（x﹣2）2+3的图象，可以将函数y＝﹣（x﹣3）2的图象（）A．向右平移1个单位，再向上平移3个单位B．向右平移1个单位，再向下平移3个单位C．向左平移1个单位，再向上平移3个单位D．向左平移1个单位，再向下平移3个单位【知识点5 二次函数图象的对称变换】2y ax bx c=++关于x轴对称，得到2y ax bx c=−−−；关于y轴对称，得到2y ax bx c=−+；()2y a x h k=−+关于x轴对称，得到()2y a x h k=−−−；关于y轴对称，得到()2y a x h k=++；2y ax bx c=++关于原点对称后，得到的解析式是2y ax bx c=−+−；()2y a x h k=−+关于原点对称后，得到的解析式是()2y a x h k=−+−；【题型5 二次函数图象的对称变换】【例5】在同一平面直角坐标系中，若抛物线y＝x2+（2a﹣b）x+b+1与y＝﹣x2+（a+b）x+a﹣4关于x轴对称，则a+b的值为（）A．﹣5B．3C．5D．15【变式5-1】抛物线y＝﹣（x+2）2关于y轴对称的抛物线的表达式为．【变式5-2】在平面直角坐标系中，将抛物线y＝x2+2x+3绕着原点旋转180°，所得抛物线的解析式是（）A．y＝﹣（x﹣1）2﹣2 B．y＝﹣（x+1）2﹣2C．y＝﹣（x﹣1）2+2D．y＝﹣（x+1）2+2【题型6 利用二次函数的性质判断结论】【例6】对于抛物线y＝﹣2（x+1）2+3，下列结论：①抛物线的开口向下；②对称轴为直线x＝1：③顶点坐标为（﹣1，3）；④x＞﹣1时，y随x的增大而减小，其中正确结论的个数为（）A．1B．2C．3D．4【变式6-1】关于抛物线y ＝x 2﹣（a +1）x +a ﹣2，下列说法错误的是（ ）A ．开口向上B ．当a ＝2时，经过坐标原点OC ．不论a 为何值，都过定点（1，﹣2）D ．a ＞0时，对称轴在y 轴的左侧【变式6-2】对于二次函数y ＝x 2﹣2mx ﹣3，有下列结论：③ 它的图象与x 轴有两个交点；②如果当x ≤﹣1时，y 随x 的增大而减小，则m ＝﹣1；③如果将它的图象向左平移3个单位后过原点，则m ＝1；④如果当x ＝2时的函数值与x ＝8时的函数值相等，则m ＝5．其中一定正确的结论是 ．（把你认为正确结论的序号都填上）【题型7 利用二次函数的性质比较函数值】【例7】已知二次函数y ＝x 2﹣2x ﹣3的自变量x 1，x 2，x 3对应的函数值分别为y 1，y 2，y 3．当﹣1＜x 1＜0， 1＜x 2＜2，x 3＞3时，y 1，y 2，y 3三者之间的大小关系是（ ）A ．y 1＜y 2＜y 3B ．y 2＜y 3＜y 1C ．y 3＜y 1＜y 2D ．y 2＜y 1＜y 3【变式7-1】抛物线y ＝x 2+x +2，点（2，a ），（﹣1，﹣b ），（3，c ），则a ，b ，c 的大小关系是（ ）A ．c ＞a ＞bB ．b ＞a ＞cC ．a ＞b ＞cD ．无法比较大小【变式7-2】已知点A （b ﹣m ，y 1），B （b ﹣n ，y 2），C （b +m+n 2，y 3）都在二次函数y ＝﹣x 2+2bx +c 的图象上， 若0＜m ＜n ，则y 1，y 2，y 3的大小关系是（ ）A ．y 1＜y 2＜y 3B ．y 2＜y 3＜y 1C ．y 3＜y 1＜y 2D ．y 1＜y 3＜y 2 【题型8 利用二次函数的性质求字母的范围】【例8】已知抛物线y ＝﹣（x ﹣2）2+9，当m ≤x ≤5时，0≤y ≤9，则m 的值可以是（ ）A ．﹣2B ．1C ．3D ．4【变式8-1】若抛物线y ＝（x ﹣m ）（x ﹣m ﹣3）经过四个象限，则m 的取值范围是（ ）A ．m ＜﹣3B ．﹣1＜m ＜2C ．﹣3＜m ＜0D ．﹣2＜m ＜1【题型9 利用二次函数的性质求最值】【例9】若实数m 、n 满足m+n ＝2，则代数式2m 2+mn +m ﹣n 的最小值是_______．【变式9-2】抛物线y ＝ax 2+bx +3（a ≠0）过A （4，4），B （2，m ）两点，点B 到抛物线对称轴的距离记为d ，满足0＜d ≤1，则实数m 的取值范围是（ ）A ．m ≤2或m ≥3B ．m ≤3或m ≥4C ．2＜m ＜3D ．3＜m ＜4*【题型10 二次函数给定范围内的最值问题】【例10】若二次函数y ＝﹣x 2+mx 在﹣1≤x ≤2时的最大值为3，那么m 的值是（ ）A ．﹣4或72B ．﹣2√3或72C ．﹣4 或2√3D ．﹣2√3或2 √3【变式10-1】已知二次函数y ＝mx 2+2mx +1（m ≠0）在﹣2≤x ≤2时有最小值﹣2，则m ＝（ ）A ．3B ．﹣3或38C ．3或−38D ．﹣3或−38 【变式10-2】若二次函数y ＝x 2﹣2x +5在m ≤x ≤m +1时的最小值为6，那么m 的值是 ．二次函数的图象与性质— 易错精选 —1. 二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，下面五条信息：①c ＜0；②ab ＜0； ③a ﹣b +c ＞0；④2a ﹣3b ＝0；⑤c ﹣4b ＞0．你认为其中正确的个数有（ ）A ．1个B ．2个C ．3个D ．4个2. 如图是二次函数y ＝ax 2+bx +c 图象的一部分，图象过点A （﹣3，0），对称轴为直线x＝﹣1，给出四个结论：①abc ＞0；②2a ﹣b ＝0；③4ac ﹣b 2＜0；④若点B （﹣，y 1）、C （﹣，y 2）为函数图象上的两点，则y 1＞y 2；⑤am 2+bm ＜a ﹣b （m 为任意实数）；其中，正确结论的个数是（ ）A ．1B ．2C ．3D ．43. 在平面直角坐标系中，二次函数y ＝ax 2+bx +c （a ≠0）的图象如图所示，现给出以下结论：①abc ＜0；②c +2a ＜0；③9a ﹣3b +c ＝0；④a ﹣b ≥m （am +b ）（m 为实数），其中正确的结论有 ．（只填序号）4. 已知二次函数y ＝ax 2+bx+c （a≠0）的图像如图，有下列6个结论：①abc＜0；②b＜a ﹣c ；③4a+2b+c＞0；④2c＜3b ；⑤a+b＜m （am+b ），（m≠1的实数）⑥2a+b+c＞0，其中正确的结论的有_____．5. 如图是抛物线21(0)y ax bx c a =++≠图像的一部分，抛物线的顶点坐标为(1,3)A ，与x 轴的一个交点为(4,0)B ，点A 和点B 均在直线2(0)y mx n m =+≠上.①20a b +=；②>0abc ；③抛物线与x 轴的另一个交点时(4,0)−；④方程23ax bx c ++=−有两个不相等的实数根；⑤4a b c m n −+<+；⑥不等式2mx n ax bx c +>++的解集为14x <<.上述六个结论中，其中正确的结论是_____________.（填写序号即可）6. 在同一个平面直角坐标系xOy 中，二次函数211y a x =，222y a x =，233y a x 的图象如图所示，则123,,a a a 的大小关系为___________（用“>”连接）．。

一.二次函数的基本概念及性质 知识点一 二次函数的概念★一般地，形如2(b c 0)y ax bx c a a =++≠、、是常数，且的函数称为二次函数，其中x 是 ，y 是x 的函数。

知识点二。

二次函数2(0)y ax bx c a =++≠的性质（重点）配方：2y ax bx c =++题型一 函数的定义例1下列函数中，是二次函数的是（ ）A.232y x =-B.21y x x=-C.22(3)y x x =-- D.3221y x x =-+2当a 取何值时，函数22(2)1a y a x x -=--+是关于x 的二次函数？3.当m 为何值时，232(1)m m y m x --=+是二次函数？题型二 函数的图像和性质2）2247y x x =--+3．（2分）（2013•福田区一模）二次函数y=x 2﹣2x +6的顶点坐标是 ．4．请写出一个图象的对称轴是直线x=1，且经过（0，1）点的二次函数的表达式： ．5．（3分）（2017•曾都区校级模拟）如图，在平面直角坐标系中，点A 在抛物线y=x 2﹣2x +3上运动，过点A 作AB ⊥x 轴于点B ，以AB 为斜边作Rt △ABC ，则AB 边上的中线CD 的最小值为 ．例2.（3分）（2014•宿迁）若将抛物线y=x 2向右平移2个单位，再向上平移3个单位，则所得抛物线的表达式为（ ） A ．y=（x +2）2+3 B ．y=（x ﹣2）2+3 C ．y=（x +2）2﹣3 D ．y=（x ﹣2）2﹣32．（4分）将函数y ＝5x 2的图象向左平移2个单位，再向上平移3个单位，所得抛物线对应函数的表达式为 ．3.抛物线122--=x x y 可由抛物线142+-=x x y 向 平移 个单位，再向_____平移_______个单位得到．3、如图，把抛物线y=x 2沿直线y=x A 处，则平移后的抛物线解析式是（ ）A ．y=（x+1）2-1B ．y=（x+1）2+1C ．y=（x -1）2+1D ．y=（x -1）2-1例3．（2分）（2014秋•无锡期末）若A（﹣4，y1），B（﹣1，y2），C（1，y3）为二次函数y=x2+4x﹣5的图象上的三点，则y1，y2，y3的大小关系是．2．（3分）已知点（2，y1），（﹣3，y2）均在抛物线y=﹣x2+4上，则y1、y2的大小关系为（）A．y1＜y2B．y1＞y2C．y1≤y2D．y1≥y23．（3分）对于二次函数y=﹣（x+1）2﹣3，下列结论正确的是（）A．函数图象的顶点坐标是（﹣1，﹣3）B．当x＞﹣1时，y随x的增大而增大C．当x=﹣1时，y有最小值为﹣3D．图象的对称轴是直线x=1例4．二次函数y=ax2+bx+c的自变量x与函数y的对应值如下表，可判断二次函数的图象与x轴( )x…﹣1012…y…1﹣2﹣3﹣2…A．只有一个公共点B．有两个交点，且它们分别在y轴两侧C．有两个交点，且它们均在y轴同侧D．无公共点2．（3分）已知y是x的二次函数，函数y与自变量x的部分对应值如表：x…﹣2﹣1012…y…﹣2464k…观察表中的数据，则k的值为．O3．（3分）（2014•南京）已知二次函数y=ax 2+bx +c 中，函数y 与自变量x 的部分对应值如表：x … ﹣1 0 1 2 3 … y…105212…则当y ＜5时，x 的取值范围是 ．例5．已知二次函数y=ax 2+bx+c 的图象如图所示，那么一次函数y=bx+c 和反比例函数ay x=（a>0,h 函数图像在一、三象限；a<0，图像在二、四象限）在同一平面直角坐标系中的图象大致是（ ）A. B ．C ．D ．6、二次函数c bx ax y ++=2的图象如图所示，则直线y bx c =+的图象不经过（ ）Ａ．第一象限 Ｂ．第二象限 Ｃ．第三象限Ｄ．第四象限例6．（3分）二次函数y＝ax2+bx+c的图象如图所示，下列结论错误的是（）A．函数有最小值B．当﹣1＜x＜2时，y＞0C．a+b+c＜0D．当x＜﹣1时，y随x的增大而减小2．（3分）已知二次函数y=ax2+bx+c的图象如图所示，则下列结论：①ac＞0；②a+b=0；③当x＜时，y随x增大而增大；④a﹣b+c＜0，其中正确的个数有（）A．4个B．3个C．2个D．1个3．如图，是二次函数y=ax2+bc+c的图象，下列结论中：①a＞0②2a+b=0③b2﹣4av＞0④a+b+c＜0⑤9a+3b+c=0，其中正确的个数是( )A．1B．2C．3D．44．二次函数y=ax2+bx+c（a，b，c是常数，a≠0）图象的对称轴是直线x=1，其图象的一部分如图所示．对于下列说法：①abc＜0；②a﹣b+c＜0；③3a+c＜0；④当﹣1＜x＜3时，y＞0．其中正确的是（把正确的序号都填上）．5、二次函数y=ax2+bx+c（a≠0）的图象如图所示，其对称轴为x=1，有如下结论：①c＜1；①2a+b=0；①b2＜4ac；①若方程ax2+bx+c=0的两根为x1，x2，则x1+x2=2，则正确的结论是（）A．①① B．①① C．①① D．①①课后练习1．（3分）（2015•苏州一模）二次函数y=（x ﹣2）2+1的图象的顶点坐标是（ ） A ．（2，1） B ．（﹣2，1）C ．（2，﹣1）D ．（﹣2，﹣1）2．（3分）把抛物线y=2x 2+1向左移1个单位，所得新抛物线的函数表达式为 ．3．在平面直角坐标系中，将二次函数y=﹣2x 2的图象向右平移1个单位长度，所得图象的函数关系式是__________．4．（3分）设A （﹣2，y 1），B （1，y 2），C （2，y 3）是抛物线y=﹣（x +1）2+a 上的三点，则y 1，y 2，y 3的大小关系为（ ） A ．y 1＞y 2＞y 3 B ．y 1＞y 3＞y 2C ．y 3＞y 2＞y 1D ．y 3＞y 1＞y 25．（3分）已知二次函数y=ax 2+bx +c 中，函数y 与自变量x 的部分对应值如表：x … ﹣2 ﹣1 0 1 2 … y…1771﹣11…则当y ＜7时，x 的取值范围是 ．6．抛物线y=ax 2+bx+c 上部分点的横坐标x ，纵坐标y 的对应值如下表：x … ﹣3 ﹣2 ﹣1 0 1 … y … ﹣60 4 6 6 … 容易看出，（﹣2，0）是它与x 轴的一个交点，则它与x 轴的另一个交点的坐标为 ．7. 把抛物线1)1(2---=x y 向 平移 个单位，再向_____平移_______个单位得到抛物线3)2(2-+-=x y8．（3分）如图是二次函数y=ax 2+bx +c 图象的一部分，其对称轴为直线x=﹣1，且过点（﹣3，0），下列说法：①abc ＜0；②2a ﹣b=0；③4a +2b +c ＜0；④若（﹣5，y 1），（2.5，y 2）是抛物线上两点，则y 1＞y 2，其中说法正确的是（ ）A ．①②③B ．②③C ．①②④D ．①②③④9、小明从右边的二次函数2y ax bx c =++图像中，观察得出了下面的五条信息： ①0a <，②0c =，③函数的最小值为3-，④当0x <时，0y >， ⑤当1202x x <<<时，12y y >①对称轴是直线x=2． 你认为其中正确的个数为（ ）Ａ．2Ｂ．3Ｃ．4Ｄ．510．如图，平行于x 轴的直线AC 分别交函数y 1=x 2与y 2=的图象于B ，C 两点，过点C作y 轴的平行线交y 1的图象于点D ，直线DE ∥AC ，交y 2的图象于点E ，则=__________．211．（3分）如图，在平面直角坐标系中，点A在第二象限，以A为顶点的抛物线经过原点，与x轴负半轴交于点B，对称轴为直线x=﹣1，点C在抛物线上，且位于点A、B之间（C不与A、B重合）．若△ABC的周长为m，四边形AOBC的周长为（用含m 的式子表示）．12．（3分）如图，把抛物线y=x2平移得到抛物线m，抛物线m经过点A（﹣6，0）和原点O（0，0），它的顶点为P，它的对称轴与抛物线y=x2交于点Q，则图中阴影部分的面积为．。

二次函数的图象与解析式一、二次函数的图象1．二次函数图象与系数的关系 （1）a 决定抛物线的开口方向及开口大小 正负性决定开口方向，绝对值大小决定开口大小．a 越大，抛物线开口越小；温馨提示：几条抛物线的解析式中，若a 相等，则其形状相同，图象经过平移、中心对称（旋转180︒）a 不变．（2）b 和a 共同决定抛物线对称轴的位置（口诀：左同右异）（3）c 的大小决定抛物线与y 轴交点的位置（抛物线与y 轴的交点坐标为()0c ，） 2．二次函数的图形信息（1）根据抛物线的开口方向判断a 的正负性． （2）根据抛物线的对称轴判断2ba-的大小． （3）根据抛物线与y 轴的交点，判断c 的大小．（4）根据抛物线与x 轴有无交点，判断24b ac -的正负性．（5）根据抛物线所经过的已知坐标的点，可得到关于a b c ，，的等式． （6）根据抛物线的顶点，判断244ac b a-的大小2.二次函数图象的画法若是无图，建议画出图象然后根据图象来分析进行解答，数形结合是解答压轴题的终极方法，因为二次函数的图象能极大的方便做题，简易绘图法：根据以下五条就可以画图二次函数的简易图象 ①a 的正负性，看图形的开口方向是往上还是往下 ②c 的正负性，看图象与y 轴的交点是在正半轴还是负半轴 ③△的正负性，看图象与x 轴有无交点 ④对称轴的位置，看a 和b 的符号是否一致 压轴题绘图法：因为压轴题的作图需要精准，以帮助解答，所以需要画出带刻度的坐标系 ①利用对称轴公式，计算出对称轴，然后画出图形的对称轴②将对称轴代入解析式，算出顶点的纵坐标（若不为整数，则舍弃这一步） ③找出与y 轴交点，并利用对称轴画出对称点，④令0y =，算出与x 轴两个交点（若不为整数，则舍弃这一步） ⑤利用对称轴画出一条尽量对称且平滑的曲线三、二次函数的图象及性质1． 二次函数2y ax bx c =++0a ≠（）或2()y a x h k =-+（0a ≠）的性质（1）开口方向：00a a >⇔⎧⎨<⇔⎩向上向下（2）对称轴：2bx a=-（或x h =） （3）顶点坐标：24(,)24b ac b a a--（或(,)h k ）（4）最值：0a >时有最小值244ac b a -（或k ）（如图1）； 0a <时有最大值244ac b a-（或k ）（如图2）；⑸单调性：二次函数2y ax bx c =++（0a ≠）的变化情况（增减性） ①如图1所示，当0a >时，对称轴左侧2bx a<-，y 随着x 的增大而减小，在对称轴的右侧2bx a>-， y 随x 的增大而增大；②如图2所示，当0a >时，对称轴左侧2bx a<-， y 随着x 的增大而增大，在对称轴的右侧2b x a>-， y 随x 的增大而减小；⑹与坐标轴的交点：①与y 轴的交点：（0，C ）；②与x 轴的交点：使方程20ax bx c ++=（或2()0a x h k -+=）成立的x 值．考点一：根据二次函数的定义确定参数的值☞考点说明：根据二次函数的定义反求参数，一般情况下会结合在综合题中处，也有可能以填空题的形式出现，考察点在二次项系数不为零【例1】 函数()()2223ay a x a x a -=++-+．当______a =，它为二次函数；当____a =，它为一次函数．【例2】 若抛物线2(1)mmy m x -=-开口向下，则______m =考点二：二次函数的对称轴☞考点说明：在求二次函数的对称轴时，根据解析式的不同，求法也不尽相同，并不仅仅只有2bx a=-的这一种求法，需灵活掌握，一般情况下，以选择、填空出现的可能性较大。

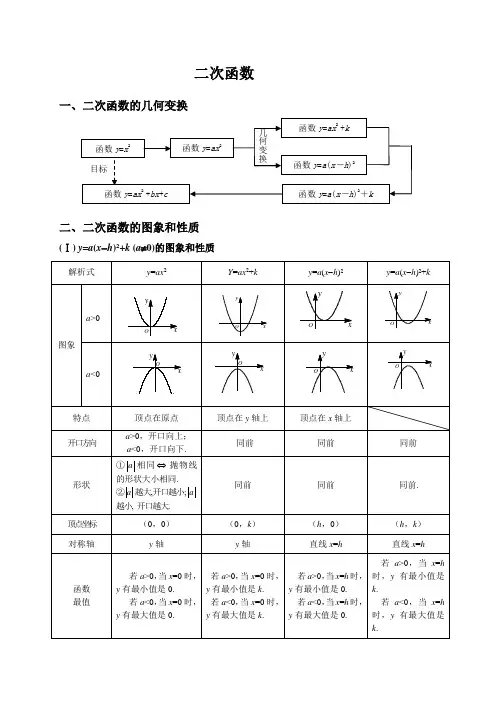
二次函数一、二次函数的几何变换二、二次函数的图象和性质(Ⅰ) y=a(x-h)2+k (a≠0)的图象和性质(Ⅱ) y=ax2+bx+c (a≠0)的图象和性质(Ⅲ) a 、b 、c 的符号对抛物线形状位置的影响三、待定系数法求二次函数的解析式1、一般式：c bx ax y ++=2.已知图像上三点或三对x 、y 的值，通常选择一般式。

2、顶点式：()k h x a y +-=2.已知图像的顶点或对称轴，通常选择顶点式。

3、交点式：已知图像与x 轴的交点横坐标1x 、2x ，通常选用交点式：()()21x x x x a y --=。

4、顶点在原点，可设解析式为y=ax 2。

5、对称轴是y 轴（或者顶点在y 轴上），可设解析式为y= ax 2+c 。

6、顶点在x 轴上，可设解析式为()2h x a y -=。

7、抛物线过原点，可设解析式为y=ax2+bx 。

四、抛物线的对称性1、抛物线与x 轴有两个交点（x 1,0）（x 2,0），则对称轴为x=2x x 21+。

2、抛物线上有不同的两个交点（m ，a ）（n,a ），则对称轴为x=2nm +。

3、抛物线c bx ax y ++=2（a ≠0）与y 轴交点关于对称轴的对称点为(ab-, c)。

五、二次函数与一元二次方程的关系对于抛物线c bx ax y ++=2（a ≠0），令y=0，即为一元二次方程02=++c bx ax ，一元二次方程的解就是二次函数与x 轴交点的横坐标。

要分三种情况：1、 判别式△=b 2-4ac ＞0⇔抛物线与x 轴有两个不同的交点（ab 24acb -2+，0）（a b 24ac b --2，0）。

有韦达定理可知x 1+x 2=a b - ，x 1·x 2=ac 。

2、 判别式△=b 2-4ac=0⇔抛物线与x 轴有一个交点（ab 2-，0）。

3、 判别式△=b 2-4ac=0⇔抛物线与x 轴无交点。

六、二次函数与一元二次不等式的关系1、a ＞0：（1）02＞c bx ax ++的解集为：x ＜x 1或x ＞x 2（x 1＜x 2）。

二次函数专题一：二次函数的图象与性质考点1.二次函数图象的对称轴和顶点坐标二次函数的图象是一条抛物线，它的对称轴是直线x=-2b a ，顶点坐标是（-2ba，244ac b a -）.例 1 已知，在同一直角坐标系中，反比例函数5y x=与二次函数22y x x c =-++的图像交于点(1)A m -，．（1）求m 、c 的值；（2）求二次函数图像的对称轴和顶点坐标.考点2.抛物线与a 、b 、c 的关系抛物线y=ax 2+bx+c 中，当a>0时，开口向上，在对称轴x=-2ba的左侧y 随x 的增大而减小，在对称轴的右侧，y 随x 的增大而增大；当a<0时，开口向下，在对称轴的右侧，y 随x 的增大而增大，在对称轴的右侧，y 随x 的增大而减小.例2 已知2y ax bx =+的图象如图1所示，则y ax b =-的图象一定过（ ）A ．第一、二、三象限B ．第一、二、四象限C ．第二、三、四象限D ．第一、三、四象限考点3.二次函数的平移当k>0（k<0）时，抛物线y=ax 2+k （a ≠0）的图象可由抛物线y=ax 2向上（或向下）平移|k|个单位得到；当h>0（h<0）时，抛物线y=a （x-h ）2（a ≠0）的图象可由抛物线y=ax 2向右（或向左）平移|h|个单位得到.例3 把抛物线y=3x 2向上平移2个单位，得到的抛物线是（ ） A.y=3（x+2）2 B.y=3（x-2）2 C.y=3x 2+2 D.y=3x 2-2图1专题练习一1.对于抛物线y=13-x 2+103x 163-，下列说法正确的是（ ） A.开口向下，顶点坐标为（5，3） B.开口向上，顶点坐标为（5，3） C.开口向下，顶点坐标为（-5，3） D.开口向上，顶点坐标为（-5，3） 2.若抛物线y=x 2-2x+c 与y 轴的交点为（0，-3），则下列说法不正确的是（ ） A.抛物线开口向上 B.抛物线的对称轴是x=1 C.当x=1时，y 的最大值为-4D.抛物线与x 轴交点为（-1，0），（3，0）3.将二次函数y=x 2的图象向左平移1个单位长度，再向下平移2个单位长度后，所得图象的函数表达式是________.4.小明从图2所示的二次函数2y ax bx c =++的图象中，观察得出了下面五条信息：①0c <；②0abc >；③0a b c -+>；④230a b -=；⑤40c b ->，你认为其中正确信息的个数有_______.（填序号）专题复习二：二次函数表达式的确定 考点1.根据实际问题模型确定二次函数表达式例1 如图1，用一段长为30米的篱笆围成一个一边靠墙（墙的长度不限）的矩形菜园ABCD ，设AB 边长为x 米，则菜园的面积y （单位：米2）与x （单位：米）的函数关系式为 （不要求写出自变量x 的取值范围）．考点2.根据抛物线上点的坐标确定二次函数表达式1.若已知抛物线上三点的坐标，则可用一般式：y=ax 2+bx+c （a ≠0）；2.若已知抛物线的顶点坐标或最大（小）值及抛物线上另一个点的坐标，则可用顶点式：y=a （x-h ）2+k （a ≠0）；3.若已知抛物线与x 轴的两个交点坐标及另一个点，则可用交点式：y=a （x-x 1）（x-x 2）（a ≠0）. 例2 已知抛物线的图象以A （-1，4）为顶点，且过点B （2，-5），求该抛物线的表达式.图2ABCD图1菜园墙例3 已知一抛物线与x 轴的交点是A （-2，0）、B （1，0），且经过点C （2，8）. （1）求该抛物线的解析式； （2）求该抛物线的顶点坐标. 专项练习二1.由于世界金融危机的不断蔓延，世界经济受到严重冲击.为了盘活资金，减少损失，某电器商场决定对某种电视机连续进行两次降价.若设平均每次降价的百分率是x ，降价后的价格为y 元，原价为a 元，则y 与x 之间的函数表达式为（ ）A.y=2a （x-1）B.y=2a （1-x ）C.y=a （1-x 2）D.y=a （1-x ）22.如图2，在平而直角坐标系xOy 中，抛物线y=x 2+bx+c 与x 轴交于A 、B 两点，点A 在x 轴负半轴，点B 在x 轴正半轴，与y 轴交于点C ，且tan ∠ACO=12，CO=BO ，AB=3，则这条抛物线的函数解析式是 ．3.对称轴平行于y 轴的抛物线与y 轴交于点（0，-2），且x=1时，y=3；x=-1时y=1， 求此抛物线的关系式.4.推理运算：二次函数的图象经过点(03)A -，，(23)B -，，(10)C -，． （1）求此二次函数的关系式； （2）求此二次函数图象的顶点坐标；（3）填空：把二次函数的图象沿坐标轴方向最少．．平移 个单位，使得该图象的顶点在原点． 专题三：二次函数与一元二次方程的关系考点1.根据二次函数的自变量与函数值的对应值，确定方程根的范围一元二次方程ax 2+bx+c=0就是二次函数y=ax 2+bx+c 当函数y 的值为0时的情况.例1 根据下列表格中二次函数y=ax 2+bx+c 的自变量x 与函数值y 的对应值，判断方程ax 2+bx+c=0（a ≠0,a,b,c,为常数）的一个解x 的范围是（ ）x6.17 6.18 6.19 6.202y ax bx c =++0.03- 0.01- 0.02 0.04Ａ．6 6.17x <<Ｂ．6.17 6.18x << Ｃ．6.18 6.19x <<Ｄ．6.19 6.20x <<图2考点2.根据二次函数的图象确定所对应的一元二次方程的根.二次函数y=ax 2+bx+c 的图象与x 轴的交点有三种情况：有两个交点、一个交点、没有交点；当二次函数y=ax 2+bx+c 的图象与x 轴有交点时，交点的横坐标就是当y=0时自变量x 的值，即一元二次方程ax 2+bx+c=0的根.例2 已知二次函数y=-x 2+3x+m 的部分图象如图1所示，则关于x 的一元二次方程-x 2+3x+m=0的解为________.考点3.抛物线的交点个数与一元二次方程的根的情况当二次函数y=ax 2+bx+c 的图象与x 轴有两个交点时，则一元二次方程ax 2+bx+c=0有两个不相等的实数根；当二次函数y=ax 2+bx+c 的图象与x 轴有一个交点时，则一元二次方程ax 2+bx+c=0有两个相等的实数根；当二次函数y=ax 2+bx+c 的图象与x 轴没有交点时，则一元二次方程ax 2+bx+c=0没有实数根.反之亦然.例3 在平面直角坐标系中，抛物线21y x =-与x 轴的交点的个数是（ ） A.3B.2C.1D.0专项练习三1.抛物线y=kx 2-7x-7的图象和x 轴有交点，则k 的取值范围是________.2.已知二次函数22y x x m =-++的部分图象如图2所示，则关于x 的一元二次方程220x x m -++=的解为 ．3.已知函数2y ax bx c =++的图象如图3所示，那么关于x 的方程220ax bx c +++= 的根的情况是（ ）A.无实数根B.有两个相等实数根C.有两个异号实数根D.有两个同号不等实数根4. 二次函数2(0)y ax bx c a =++≠的图象如图4所示，根据图象解答下列问题：（1）写出方程20ax bx c ++=的两个根．（2）写出不等式20ax bx c ++>的解集．（3）写出y 随x 的增大而减小的自变量x 的取值范围．（4）若方程2ax bx c k ++=有两个不相等的实数根，求k 的取值范围．图1。

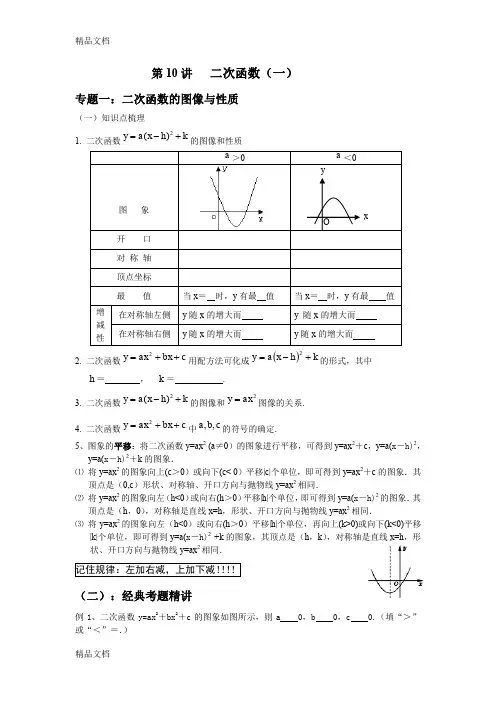
第10讲 二次函数（一）专题一：二次函数的图像与性质（一）知识点梳理1. 二次函数2()y a x h k =-+的图像和性质 a ＞02. 二次函数c bx ax y ++=2用配方法可化成()k h x a y +-=2的形式，其中 h ＝ ， k ＝ .3. 二次函数2()y a x h k =-+的图像和2ax y =图像的关系.4. 二次函数c bx ax y ++=2中c b a ,,的符号的确定. 5、图象的平移：将二次函数y=ax 2 (a ≠0）的图象进行平移，可得到y=ax 2＋c ，y=a(x －h)2，y=a(x －h)2＋k 的图象．⑴ 将y=ax 2的图象向上(c ＞0）或向下(c< 0）平移|c|个单位，即可得到y=ax 2＋c 的图象．其顶点是（0,c ）形状、对称轴、开口方向与抛物线y=ax 2相同． ⑵ 将y=ax 2的图象向左（h<0）或向右(h ＞0）平移|h|个单位，即可得到y=a(x －h)2的图象．其顶点是（h ，0），对称轴是直线x=h ，形状、开口方向与抛物线y=ax 2相同．⑶ 将y=ax 2的图象向左（h<0）或向右(h ＞0）平移|h|个单位，再向上(k>0)或向下(k<0)平移|k|个单位，即可得到y=a(x －h)2 +k 的图象，其顶点是（h ，k ），对称轴是直线x=h ，形状、开口方向与抛物线y=ax 2相同．（二）：经典考题精讲例1、二次函数y=ax 2＋bx 2＋c 的图象如图所示，则a 0，b 0，c 0.（填“＞”或“＜”＝．）例2、二次函数y=ax 2＋bx ＋c 与一次函数y=ax ＋c 在同一坐标系中的图象大致是图中的（ ）例3、在同一坐标系中，函数y=ax 2＋bx 与y=xb的图象大致是图中的（ ）例4、如图所示的是桥梁的两条钢缆具有相同的抛物线形状．按照图中建立的直角坐标系，左面的一条抛物线可以用y=0．0225x 2＋0．9x ＋10表示，而且左右两条抛物线关于y 轴对称，你能写出右面钢缆的表达式吗？例5、图中各图是在同一直角坐标系内，二次函数y=ax 2＋（a ＋c ）x ＋c 与一次函数y=ax ＋c 的大致图象，有且只有一个是正确的，正确的是（ ）例6、抛物线y=ax 2＋bx ＋c 如图所示，则它关于y 轴对称的抛物线的表达式是 ．例7、已知二次函数y=（m －2）x 2＋（m ＋3）x ＋m ＋2的图象过点（0，5）（1）求m 的值，并写出二次函数的表达式； （2）求出二次函数图象的顶点坐标、例8、 如图所示，有一边长为5cm 的正方形ABCD 和等腰三角形PQR ，PQ=PR=5cm ，QR=8cm ，点B 、C 、Q 、R 在同一直线ι上．当CQ 两点重合时，等腰△PQR 以1cm/秒的速度沿直线ι按箭头所示方向开始匀速运动，t 秒后，正方形ABCD 与等腰△PQR 重合部分的面积为Scm 2．解答下列问题：（1）当t=3秒时，求S 的值； （2）当t=5秒时，求S 的值；三：拓展与应用1. 抛物线()22-=x y 的顶点坐标是 .2．将抛物线23y x =-向上平移一个单位后，得到的抛物线解析式是 ．3. 如图所示的抛物线是二次函数2231y ax x a =-+- 的图象，那么a 的值是 ．4.二次函数2(1)2y x =-+的最小值是（ ） A.－2 B.2 C.－1 D.15. 请写出一个开口向上，对称轴为直线x ＝2，且与y 轴的交点坐标为(0，3)的抛物线的解析式 .6.已知二次函数22y x x m =-++的部分图象如右图所示，则关于x 的一元二次方程220x x m -++=的解为 ．7.已知函数y=x 2-2x-2的图象如图所示，根据其中提供的信息，可求得使y≥1成立的x 的取值范围是（ ）A ．-1≤x≤3B ．-3≤x≤1C ．x≥-3D ．x≤-1或x≥38. 二次函数c bx ax y ++=2（0≠a ）的图象如图所示，则下列结论： ①a ＞0； ②c ＞0； ③ b 2-4a c ＞0，其中正确的个数是( )A. 0个B. 1个C. 2个D. 3个 第3题图第6题图9. 已知二次函数243y ax x=-+的图象经过点（－1，8）.（1）求此二次函数的解析式；（2）根据（1）填写下表.在直角坐标系中描点，并画出函数的图象；（3）根据图象回答：当函数值y<0时，x的取值范围是什么？专题二：二次函数与一元二次方程（一）：【知识梳理】1．二次函数与一元二次方程的关系：（1）一元二次方程ax2+bx+c=0就是二次函数y=ax2+bx+c当函数y的值为0时的情况．（2）二次函数y=ax2+bx+c的图象与x轴的交点有三种情况：有两个交点、有一个交点、没有交点；当二次函数y=ax2+bx+c的图象与x轴有交点时，交点的横坐标就是当y=0时自变量x的值，即一元二次方程ax2＋bx＋c=0的根．（3）当二次函数y=ax2+bx+c的图象与 x轴有两个交点时，则一元二次方程y=ax2+bx+c 有两个不相等的实数根；当二次函数y=ax2+bx+c的图象与x轴有一个交点时，则一元二次方程ax2＋bx＋c＝0有两个相等的实数根；当二次函数y＝ax2+ bx+c的图象与x轴没有交点时，则一元二次方程y=ax2+bx+c没有实数根（二）：【经典考题剖析】1.已知二次函数y=x2－6x+8，求：（1）抛物线与x轴J轴相交的交点坐标；（2）抛物线的顶点坐标；（3）画出此抛物线图象，利用图象回答下列问题：①方程x2－6x＋8=0的解是什么？②x取什么值时，函数值大于0？③x取什么值时，函数值小于0？2.已知抛物线y＝x2－2x－8，（1）求证：该抛物线与x轴一定有两个交点；（2）若该抛物线与x轴的两个交点分别为A、B，且它的顶点为P，求△ABP的面积．3.如图所示，直线y=-2x+2与x 轴、y 轴分别交于点A 、B ，以线段AB 为直角边在第一象限内作等腰直角△ABC ，∠BAC=90o， 过C 作CD ⊥x 轴，垂足为D （1）求点A 、B 的坐标和AD 的长（2）求过B 、A 、D 三点的抛物线的解析式4.如图，在矩形ABCD 中，AB=6cm ，BC=12cm ，点P 从点A 出发，沿AB 边向点B 以1cm/s 的速度移动，同时点Q 从点B 出发，沿BC 边向点C 以2cm/s 的速度移动，回答下列问题：（1） 设运动后开始第t （单位：s ）时，五边形APQCD 的面积为S（单位：cm 2），写出S 与t 的函数关系式，并指出自变量t 的取值范围 （2）t 为何值时S 最小？求出S 的最小值5. 如图，直线334y x k=+(0)k >与x 轴、y 轴分别交于A 、B 两点，点P 是线段AB 的中点，抛物线283y x bx c =-++经过点A 、P 、O （原点）。

二次函数知识点、考点、典型试题集锦(带详细解析答案)考点1：二次函数的图象和性质一、考点讲解：1．二次函数的定义：形如c bx ax y ++=2（a ≠0，a ，b ，c 为常数）的函数为二次函数．2．二次函数的图象及性质：⑴ 二次函数y=ax 2(a ≠0）的图象是一条抛物线，其顶点是原点，对称轴是y 轴；当a ＞0时，抛物线开口向上，顶点是最低点；当a ＜0时，抛物线开口向下，顶点是最高点；a 越小，抛物线开口越大．y=a(x －h)2＋k 的对称轴是x=h ，顶点坐标是（h ，k ）。

⑵ 二次函数c bx ax y ++=2的图象是一条抛物线．顶点为（－2b a ，244ac b a -），对称轴x=－2b a ；当a ＞0时，抛物线开口向上，图象有最低点，且x ＞－2b a ，y 随x 的增大而增大，x ＜－2ba ，y 随x 的增大而减小；当a ＜0时，抛物线开口向下，图象有最高点，且x ＞－2b a ，y 随x 的增大而减小，x ＜－2ba ，y 随x 的增大而增大．⑶ 当a ＞0时，当x=－2b a 时，函数有最小值244ac b a -；当a ＜0时，当 x=－2b a 时，函数有最大值244ac b a -。

3．图象的平移：将二次函数y=ax 2 (a ≠0）的图象进行平移，可得到y=ax 2＋c ，y=a(x －h)2，y=a(x －h)2＋k 的图象．⑴ 将y=ax 2的图象向上(c ＞0）或向下(c< 0）平移|c|个单位，即可得到y=ax 2＋c 的图象．其顶点是（0,c ），形状、对称轴、开口方向与抛物线y=ax 2相同．⑵ 将y=ax 2的图象向左（h<0）或向右(h ＞0）平移|h|个单位，即可得到y=a(x －h)2的图象．其顶点是（h ，0），对称轴是直线x=h ，形状、开口方向与抛物线y=ax 2相同．⑶ 将y=ax 2的图象向左（h<0）或向右(h ＞0）平移|h|个单位，再向上(k>0)或向下(k<0)平移|k|个单位，即可得到y=a(x －h)2 +k 的图象，其顶点是（h ，k ），对称轴是直线x=h ，形状、开口方向与抛物线y=ax 2相同．注意：二次函数y=ax 2 与y=－ax 2 的图像关于x 轴对称。

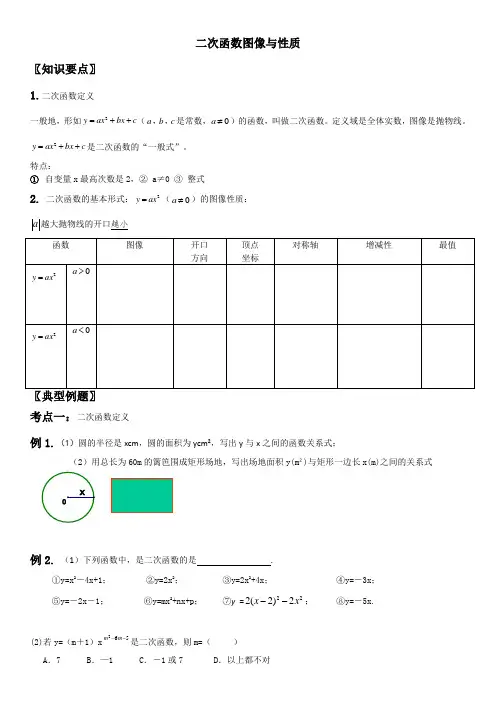
二次函数图像与性质〖知识要点〗 1.二次函数定义一般地，形如2y ax bx c =++（a b c ，，是常数，0a ≠）的函数，叫做二次函数。

定义域是全体实数，图像是抛物线。

2y ax bx c =++是二次函数的“一般式”。

特点：① 自变量x 最高次数是2，② a ≠0 ③ 整式2. 二次函数的基本形式：2y ax =（0a ≠）的图像性质：a 越大抛物线的开口越小考点一：二次函数定义例1.（1）圆的半径是xcm ，圆的面积为ycm²，写出y 与x 之间的函数关系式；（2）用总长为60m 的篱笆围成矩形场地，写出场地面积y(m ²)与矩形一边长x(m)之间的关系式例2. （1）下列函数中，是二次函数的是 .①y=x 2－4x+1； ②y=2x 2； ③y=2x 2+4x ； ④y=－3x ； ⑤y=－2x －1； ⑥y=mx 2+nx+p ； ⑦y =222(2)2x x --；⑧y=－5x.(2)若y=（m ＋1）x562--m m 是二次函数，则m=（ ）A ．7B ．—1C ．－1或7D ．以上都不对(3)函数)1(432-=x y 的自变量x 的取值范围是 ； (4)已知二次函数3)12()1(2+++-=x m x m y ，当x=1时，y=3，则其表达式为 ；（5）已知二次函数8-10-2x xy +=，当x=________________时,函数值y 为1.考点二：2y ax =（0a ≠）的图像性质例3.作二次函数2x 2y =的图像观察图象,你发现了:例4.（1） 函数y=-x 2的图像是一条______线,开口向_______,对称轴是______, 顶点是________, 顶点是图像最_____点,表示函数在这点取得最_____值。

函数y=x 2 的图像的开口方向________,对称轴________,顶点_______.（2）．关于213y x =，2y x =，y=-3x 2的图像，开口最大的是 ．例5已知抛物线y=ax 2经过点A （-2，-8）.（1）求此抛物线的函数解析式；（2）判断点B （-1，- 4）是否在此抛物线 ；（3）求出此抛物线上纵坐标为-6的点的坐标.例6已知二次函数mm m +=2xy （1）当m 取何值时它的图象开口向上。

九年级数学二次函数的图像与性质知识点讲解及练习一、知识结构1.任意抛物线y a x h k =-+()2可以由抛物线y ax =2经过适当的平移得到，移动规律可简记为：[左加右减，上加下减]，具体平移方法如下表所示。

2.在画y ax bx c =++2的图象时，可以先配方成y a x h k =-+()2的形式，然后将y ax =2的图象上（下）左（右）平移得到所求图象，即平移法； 基础演练：1、抛物线y=-4x 2-2的开口向 ，对称轴是 ，顶点坐标是 。

2、抛物线y=3（x+1）2的开口向 ，对称轴是 ，顶点坐标是 ，最 值为3、二次函数y=-2（x-1）2+3的开口向 ，对称轴是 ，顶点坐标是 ，当x 时，函数y 随x 的值的增大而增大；当x= 时，函数有最大值为 。

4、将抛物线y=－2x 2 向右平移1个单位，再向上平移3个单位，所得抛物线是 。

5、抛物线y=-4(x-2)2+3 可由抛物线y=-4x 2向 平移 个单位，再向 平移 个单位得到的。

二、典型例题：1、已知二次函数y=ax 2+bx+c(a≠0)的图像如图所示，有下列5个结论：xy33221141-1-2-O ①abc ＞0 ②b ＜a+c ③4a+2b+c ＞0 ④2c ＜3b ⑤a+b ＞m(am+b)(m≠1的实数) 其中哪些正确的结论是2、二次函数y=ax 2+bx+c 的图象如图所示，根据图象解答下列问题：（1）写出方程ax 2+bx+c=0的两个根． （2）写出不等式ax 2+bx+c ＞0的解集．（3）若方程ax 2+bx+c=k 有两个不相等的实数根，求k 的取值范围． 题组二： 1.抛物线21(1)22y x =--+的顶点坐标是 ，对称轴是 ，开口向 。

当x时，y 随x 的增大而减小，当x 时，y 有最 值 ；抛物线与x 轴的交点坐标为 与 ，抛物线与y 轴的交点坐标为2.抛物线如图所示：当x =________时，y =0，当x <-1，或x >3时，y _______0； 当-1<x <3时，y ______0；当x =_______时，y 有最______值。

专题两位同学做法正确的是（ ）A ．甲正确，乙不正确B ．甲不正确，乙正确C ．甲、乙都正确D ．甲、乙都不正确【变式1-3】（2023·广东·九年级专题练习）4．用配方法把二次函数2231y x x =-+写成()2y a x h k =-+的形式为(1)完成下表，并在方格纸中画该函数的图象；…1-0123………(2)根据图象，完成下列填空：①当1x >时，y 随x 的增大而___________②当0y <时，x 的取值范围是____________【变式3-1】．（2023春·广东河源·九年级校考阶段练习）10．已知函数图象如图所示，根据图象可得：(1)抛物线顶点坐标___________．(2)对称轴为___________．(3)当x =___________时，y 有最大值是___________．(4)当___________时，y 随着 x 的增大而增大．(5)当___________时，0y >．【变式3-2】（2023春·河南安阳·九年级校考阶段练习）11．已知抛物线2246y x x =-++．(1)请用配方法将2246y x x =-++化为()2y a x h k =-+的形式，并直接写出对称轴；(2)在如图所示的平面直角坐标系中，画出2246y x x =-++的图象；(3)该抛物线沿x 轴向左或向右平移m （0m >）个单位长度后经过原点，求m 的值．【变式3-3】（2023·上海松江·统考一模）12．已知二次函数2241y x x =--．(1)用配方法求这个二次函数的顶点坐标；(2)在所给的平面直角坐标系xOy 中（如图），画出这个二次函数的图像；(3)请描述这个二次函数图像的变化趋势．【知识点2 二次函数解析式的表示方法】（1）一般式：y ＝ax 2＋bx ＋c (其中a ，b ，c 是常数，a ≠0)；（2）顶点式：y ＝a (x －h )2＋k (a ≠0)，它直接显示二次函数的顶点坐标是（h ，k ）；（3）交点式：y ＝a (x －x 1)(x －x 2)(a ≠0)，其中x 1，x 2是图象与x 轴交点的横坐标．注意：任何二次函数的解析式都可以化成一般式或顶点式，但并非所有的二次函数都可以写成交点式，只有抛物线与x 轴有交点，即240b ac -≥时，抛物线的解析式才可以用交点式表示．二次函数解析式的这三种形式可以互化．【题型4 用待定系数法求二次函数解析式】【例4】（2023春·北京海淀·九年级期末）13．已知二次函数2y ax bx c =++经过()0,5A ，()5,0B 两点，它的对称轴为直线3x =，求这个二次函数解析式．【变式4-1】（2023春·湖北恩施·九年级校考阶段练习）14．已知一条抛物线的对称轴是直线1x =，函数的最大值是2y =，且该抛物线经过坐标原点()0,0．求此抛物线的函数关系．【变式4-2】（2023春·河北承德·九年级承德市第四中学校考阶段练习）15．在二次函数2y x bx c =++中，函数y 与自变量x 的部分对应值如下表：方法二：（1）y=ax2+bx+c沿y轴平移：向上（下）平移m个单位，y=ax2+（或y=ax2+bx+c-m）．（2）y=ax2+bx+c沿x轴平移：向左（右）平移m个单位，y=ax y=a(x+m)2+b(x+m)+c（或y=a(x-m)2+b(x-m)+c．【题型5二次函数图象的平移变换】【例5】（2023·陕西榆林·统考一模）A ．224y x x =--B ．y =-D ．y =-【变式5-3】（2023春·山东烟台·九年级统考期中）20．在平面直角坐标系中，如果抛物线【题型7利用二次函数的对称轴、最值求参数】【例7】新的二次函数1y 的图像，使得当13x -<<时，1y 随x 增大而增大；当45x <<时，1y 随x 增大而减小．则实数k 的取值可以是（ ）A ．4B ．5C ．6D ．7参考答案：故答案为：0，3-，4-，3-，0；（2）观察图象，当1x >时，y 随x 的增大而增大，故答案为：①增大；②13x -<<．【点睛】本题考查二次函数的性质，解题关键是掌握二次函数图象与系数的关系，函数与方程及不等式的关系．10．(1)()32-，(2)直线3x =-（3）∵2246y x x =-++经过点()()1,0,3,0-，∴抛物线沿x 轴向左平移3个单位长度或向右平移1个单位长度后经过原点，∴1m =或3．【点睛】本题考查二次函数的顶点式、画二次函数的图象，二次函数平移的规律，解题的关键是根据掌握二次函数平移的规律．12．(1)顶点坐标()1,3-(2)见解析(3)这个二次函数图像在对称轴直线1x =左侧部分是下降的，右侧部分是上升的【分析】（1）将函数解析式化为顶点式，即可得出答案；（2）先求出几个特殊的点，然后描点连线即可；（3）根据（2）函数图像，即可得出结果．【详解】（1）解：（1）()()222241221213y x x x x x =--=--=--∴二次函数的顶点坐标()1,3-；（2）解：当0x =时，1y =-，当1y =-时，2x =，经过点()0,1-，()2,1-，顶点坐标为：()1,3-（3）解：这个二次函数图像在对称轴直线【点睛】本题主要考查二次函数的基本性质及作图方法，题关键．13．265y x x =-+【分析】根据待定系数法求解函数解析式即可．【详解】解：由题意得：322550b a a b c ⎧-=⎪⎪++=⎨，∴顶点坐标为()1,2，设抛物线解析式为()212y a x =-+，将点()0,0代入，得20a +=解得：2a =-，∴抛物线解析式为()2212y x =--+．【点睛】本题考查了待定系数法求二次函数解析式，掌握二次函数的性质是解题的关键．15．A【分析】利用待定系数法求出二次函数的解析式，即可求解．【详解】解：把点()()1,2,0,1--代入2y x bx c =++，得：121b c c -+=⎧⎨=-⎩，解得：12c b =-⎧⎨=-⎩，∴二次函数的解析式为221y x x =--，当2x =时，42211y =-⨯-=-．故选：A【点睛】本题主要考查了求二次函数的解析式，熟练掌握用待定系数法求出二次函数的解析式的方法是解题的关键．16．D【分析】设函数解析式为(3)(2)y a x x =+-，将点(1,8)-代入即可求得a 的值，可得结果．【详解】解：设抛物线函数解析式为：(3)(2)y a x x =+-，∵抛物线经过点(1,8)-，∴8(13)(12)a -=+-，解得：2a =，∴抛物线解析式为：2(3)(2)y x x =+-，整理得：22212y x x =+-，故选：D ．【点睛】本题主要考查待定系数法求二次函数的解析式，设出二次函数的交点式是解题的关键．【分析】将抛物线243y x x =-+化成顶点式，再根据“左加右减，上加下减”，采取逆推的方法可得抛物线2y x bx c =++的解析式．【详解】解：将抛物线243y xx =-+化成顶点式为()221y x =--，将抛物线243y xx =-+向左平移4个单位，再向上平移3个单位得新抛物线解析式为()22413y x =-+-+，即246y x x =++，∴抛物线2y x bx c =++的解析式为246y x x =++，4b ∴=，6c =，故选：D ．【点睛】本题主要考查了二次函数平移的特征，熟练掌握“左加右减，上加下减”是解题的关键．18．2y x =【分析】先将二次函数解析式化为顶点式，再根据二次函数图象平移规律“左加右减，上加下减”解答即可．【详解】解：将二次函数222=++y x x 化为顶点式为：()211y x =++，将二次函数()211y x =++的图象向右平移1个单位，再向下平移一个单位，得到的新图象函数的表达式为22(11)11y x x =+-+-=，故答案为：2y x =．【点睛】本题考查二次函数的平移，熟练掌握二次函数图象平移规律是解答的关键．19．B【分析】由平移的性质可得二次项的系数为2-，再结合平移后的抛物线的顶点坐标可得答案．【详解】解：∵抛物线212y x bx c =-++经过平移后得到抛物线2y ，而2y 的顶点坐标为：()1,3-，∴()222213241y x x x =-++=--+，即2241y x x =--+；【点睛】本题主要考查了二次函数的平移，轴对称变化，知识进行求解．。

二次函数知识点总结及典型例题和练习（极好）知识点一：二次函数的概念和图像 1、二次函数的概念一般地，如果)0,,(2≠++=a c b a c bx ax y 是常数，，特别注意a 不为零，那么y 叫做x 的二次函数。

)0,,(2≠++=a c b a c bx ax y 是常数，叫做二次函数的一般式。

2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线，这条曲线叫抛物线。

抛物线的主要特征：①有开口方向；②有对称轴；③有顶点。

3、二次函数图像的画法--------五点作图法：（1）先根据函数解析式，求出顶点坐标，在平面直角坐标系中描出顶点M ，并用虚线画出对称轴（2）求抛物线c bx ax y ++=2与坐标轴的交点：当抛物线与x 轴有两个交点时，描出这两个交点A,B 及抛物线与y 轴的交点C ，再找到点C 的对称点D 。

将这五个点按从左到右的顺序连接起来，并向上或向下延伸，就得到二次函数的图像。

当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D 。

由C 、M 、D 三点可粗略地画出二次函数的草图。

如果需要画出比较精确的图像，可再描出一对对称点A 、B ，然后顺次连接五点，画出二次函数的图像。

【例1】 已知函数y=x 2-2x-3，（1）写出函数图象的顶点、图象与坐标轴的交点，以及图象与 y 轴的交点关于图象对称轴的对称点。

然后画出函数图象的草图；（2）求图象与坐标轴交点构成的三角形的面积：（3）根据第（1）题的图象草图，说 出 x 取哪些值时，① y=0；② y<0；③ y>0二次函数的解析式有三种形式：（1）一般式：)0,,(2≠++=a c b a c bx ax y 是常数，（2） 交点式：当抛物线c bx ax y ++=2与x 轴有交点时，即对应的一元二次方程02=++c bx ax 有实根1x 和2x 存在时，根据二次三项式的分解因式))((212x x x x a c bx ax --=++，二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。

1.抛物线y=ax2+bx+c中，b＝4a，它的图象如图，有以下结论：①c>0；②a+b+c> 0 ③a-b+c> 0 ④b2-4ac<0 ⑤abc< 0 ；其中正确的为（）AA．①②B．①④C．①②③D．①③⑤2.当b<0时，一次函数y=ax+b与二次函数y=ax2+bx+c在同一坐标系内的图象可能是（）B3．二次函数y＝ax2＋bx＋c的图象如图所示，那么abc，b2－4ac， 2a＋b，a＋b＋c 四个代数式中，值为正数的有( ) B 123A.4个B.3个C.2个D.1个4.在同一坐标系中，函数y= ax2+c与y= cx(a<c)图象可能是图所示的( )AA B C D5.函数y=x2+bx+c与y=x的图象如图，有以下结论：①b2﹣4c＜0；②c﹣b+1=0；③3b+c+6=0；④当1＜x＜3时，x2+（b﹣1）x+c＜0．其中正确结论的个数为（） C 134A．1B．2C．3D．46．如图是二次函数y=ax2+bx+c图象的一部分，其对称轴为x=﹣1，且过点（﹣3，0）下列说法：①abc＜0；②2a﹣b=0；③4a+2b+c＜0；④若（﹣5，y1），（2，y2）是抛物线上的两点，则y1＞y2．其中说法正确的是（）DA．①②B．②③C．②③④D．①②④7.已知抛物线y ＝ax 2＋bx ＋c(a ≠0)的图象如图所示，则下列结论： ①a ，b 同号； ②当x ＝1和x ＝3时，函数值相同； ③4a ＋b ＝0; ④当y ＝－2时，x的值只能取0； 其中正确的个数是（ ）23 A ．1 B ．2 C ．3 D ．4题型八、函数解析式的求法用待定系数法求二次函数的解析式（1）一般式：c bx ax y ++=2.已知图像上三点或三对x 、y 的值，通常选择一般式. （2）顶点式：()k h x a y +-=2.已知图像的顶点或对称轴，通常选择顶点式.（3）交点式：已知图像与x 轴的交点坐标1x 、2x ，通常选用交点式：()()21x x x x a y --=.一、已知抛物线上任意三点时，通常设解析式为一般式y=ax 2+bx+c ，然后解三元方程组求解； 1．已知抛物线过A （1，0）和B （4，0）两点，交y 轴于C 点且BC ＝5，求该二次函数的解析式。

二次函数知识点总结及典型例题和练习（极好）知识点一：二次函数的概念和图像 1、二次函数的概念一般地，如果)0,,(2≠++=a c b a c bx ax y 是常数，，特别注意a 不为零，那么y 叫做x 的二次函数。

)0,,(2≠++=a c b a c bx ax y 是常数，叫做二次函数的一般式。

2、二次函数的图像二次函数的图像是一条关于abx 2-=对称的曲线，这条曲线叫抛物线。

抛物线的主要特征：①有开口方向；②有对称轴；③有顶点。

3、二次函数图像的画法--------五点作图法：（1）先根据函数解析式，求出顶点坐标，在平面直角坐标系中描出顶点M ，并用虚线画出对称轴（2）求抛物线c bx ax y ++=2与坐标轴的交点：当抛物线与x 轴有两个交点时，描出这两个交点A,B 及抛物线与y 轴的交点C ，再找到点C 的对称点D 。

将这五个点按从左到右的顺序连接起来，并向上或向下延伸，就得到二次函数的图像。

当抛物线与x 轴只有一个交点或无交点时，描出抛物线与y 轴的交点C 及对称点D 。

由C 、M 、D 三点可粗略地画出二次函数的草图。

如果需要画出比较精确的图像，可再描出一对对称点A 、B ，然后顺次连接五点，画出二次函数的图像。

【例1】 已知函数y=x 2-2x-3，（1）写出函数图象的顶点、图象与坐标轴的交点，以及图象与 y 轴的交点关于图象对称轴的对称点。

然后画出函数图象的草图；（2）求图象与坐标轴交点构成的三角形的面积：（3）根据第（1）题的图象草图，说 出 x 取哪些值时，① y=0；② y<0；③ y>0二次函数的解析式有三种形式：（1）一般式：)0,,(2≠++=a c b a c bx ax y 是常数，（2） 交点式：当抛物线c bx ax y ++=2与x 轴有交点时，即对应的一元二次方程02=++c bx ax 有实根1x 和2x 存在时，根据二次三项式的分解因式))((212x x x x a c bx ax --=++，二次函数c bx ax y ++=2可转化为两根式))((21x x x x a y --=。

【典型例题】题型一、二次函数的图像及性质 例1、填表抛物线开口对称轴顶点坐标增减性 最值性223y x =+ 232y x =- 22y x =-+23y x =--例2、如图， ① y ＝ax 2 ② y ＝bx 2 ③ y ＝cx 2④ y ＝dx 2比较a 、b 、c 、d 的大小，用“＞”连接．___________________________________ 题型二、图象的平移例3、抛物线232+-=x y 向上平移3个单位后的解析式为 ，它们的形状__________，当x = 时，y 有最 值是 。

题型三、二次函数解析式例4、二次函数k ax y +=2()0≠a 的经过点A （1，-1）、B （2，5）.⑴求该函数的表达式；⑵若点C(-2，m ),D （n ，7）也在函数的上，求m 、n 的值。

例 2 若二次函数c x x y +-=62的图像过),23(),,2(),,1(321y C y B y A +-,则321,,y y y 则的大小关系是（ ）A ．y 1＞y 2＞y 3B ．y 1＞y 3＞y 2C ．y 2＞y 1＞y 3D ．y 3＞y 1＞y 2题型三：图形的平移例3 将二次函数y =x 2的图象向下平移一个单位，则平移以后的二次函数的解析式为（ ）A ．y =x 2﹣1B ．y =x 2+1C ．y =（x ﹣1）2D ．y =（x +1）变式训练 将抛物线23y x =向上平移3个单位，再向左平移2个单位，那么得到的抛物线的解析式为（ ）A ．23(2)3y x =++ B ．23(2)3y x =-+ C ．23(2)3y x =+- D ．23(2)3y x =--题型四：二次函数c bx ax y ++=2的图象特征与c b a 、、的符号之间的关系例4 已知二次函数)0(2≠++=a c bx ax y 的图象如图1所示，则有： （1）a ___0,b___0 ,c___0 （2）b 2－4ac___0 （3）a+b+c___0 （4）a-b+c___0变式训练1 已知二次函数y =ax 2+bx +c 的图象如图2所示，其对称轴x =﹣1，给出下列结果： ①b 2＞4ac ；②abc ＞0；③2a +b =0；④a +b +c ＞0；⑤a ﹣b +c ＜0，则正确的结论是 （ ） A 、①②③④ B 、②④⑤ C 、②③④ D 、①④⑤图2变式训练2 已知二次函数2y ax bx c =++的图像如图3所示，那么一次函数y bx c =+和反y-1x图1x=122468211234O比例函数ay x=在同一平面直角坐标系中的图像大致是（ ）C D题型五:求二次函数与坐标轴交点例5 如图，二次函数y ＝x 2－4x ＋3的图象交x 轴于A 、B 两点，交y 轴于点C ， （1）求△A B C 的面积。

二次函数的图像及性质一、知识要点1.二次函数的概念：形如________________________________的函数，叫做x的二次函数．．．．。

称：a 为二次项系数，ax 2叫做二次项；b 为一次项系数， bx 叫做一次项； c 为常数项。

)0(2≠=a ax y 是二次函数的特例，此时常数b=c=________.注意：在写二次函数的关系式时，一定要寻找两个变量之间的等量关系，列出相应的函数关系式，并确定自变量的取值范围．．．．．．．．。

2.二次函数y ＝ax 2的图象是一条顶点在____________,关于__________对称的曲线，这条曲线叫做抛物线．．．。

描述抛物线常从开口方向、对称性、y 随x 的变化情况、抛物线的最高（或最低）点、抛物线与x 轴的交点等方面来描述。

①函数的定义域是_____________；②抛物线的顶点________，对称轴是_________(或称直线___________)。

③当a ＞0时，抛物线开口_______，并且向上方无限伸展。

当a ＜0时，抛物线开口_________，并且向下方无限伸展。

④函数的增减性：当a ＞0时⎩⎨⎧≥≤._____________,0__;__________,0增大而随时增大而随时x y x x y x当a ＜0时⎩⎨⎧≥≤.____________,0__;__________,0增大而随时增大而随时x y x x y x⑤当｜a ｜越大，抛物线开口_________；当｜a ｜越小，抛物线的开口_________。

⑥最大值或最小值：当a ＞0，且x ＝0时函数有___________，是___________； 当a ＜0，且x ＝0时函数有___________，是____________． 3.二次函数c ax y +=2的图象是一条顶点在____________且与____________对称的抛物线4.二次函数c bx ax y ++=2的图象是以____________________________为对称轴，顶点为___________________________的抛物线。

二次函数y=ax^2＋c(a ≠0)与y=a （x-h)^2＋k(a ≠0)的图象与性质【知识梳理】一、二次函数y=ax 2+c(a ≠0)的图象及性质1.二次函数y=ax 2+c(a ≠0)的图象（1）（2）2.二次函数y=ax 2+c(a ≠0)的图象的性质关于二次函数的性质，主要从抛物线的开口方向、顶点、对称轴、函数值的增减性以及函数的最大值或最小值等方面来研究．下面结合图象，将其性质列表归纳如下：>a 0<a 0=+≠y ax c a (0)2jjjj向上 向下 (0，c) (0，c) 3.二次函数与之间的关系；（上加下减）.的图象向上（c ＞0）【或向下（c ＜0）】平移│c │个单位得到的图象. 要点诠释：函数的图象是由函数的图象向上（或向下）平移个单位得到的，顶点坐标为(0，c)．抛物线y ＝ax 2(a ≠0)的对称轴、最值与顶点密不可分，其对称轴即为过顶点且与x 轴垂直的一条直线，其顶点横坐标x ＝0，抛物线平移不改变抛物线的形状，即a 的值不变，只是位置发生变化而已． 二、函数2()(0)y a x h a =−≠与函数2()(0)y a x h k a =−+≠的图象与性质 1.函数2()(0)y a x h a =−≠的图象与性质()20y ax a =≠()20y ax c a =+≠()20y ax a =≠()20y ax c a =+≠2(0)y ax c a =+≠2(0)y ax a =≠||c2.函数2()(0)y a x h k a =−+≠的图象与性质要点诠释：二次函数的图象常与直线、三角形、面积问题结合在一起，借助它的图象与性质．运用数形结合、函数、方程思想解决问题． 三、二次函数的平移 1.平移步骤：⑴ 将抛物线解析式转化成顶点式，确定其顶点坐标； ⑵ 保持抛物线的形状不变，将其顶点平移到处，具体平移方法如下：2.平移规律：在原有函数的基础上“值正右移，负左移；值正上移，负下移”．概括成八个字“左加右减，上加下减”．2()+(0y a x h k a =−≠）()2y a x h k =−+()h k ，2y ax =()h k，h k要点诠释：⑴沿轴平移:向上（下）平移个单位，变成（或）⑵沿x 轴平移：向左（右）平移个单位，变成（或）【考点剖析】题型一、二次函数y=ax 2+c(a ≠0)的图象及性质例1．求下列抛物线的解析式：（1）与抛物线形状相同，开口方向相反，顶点坐标是（0，-5）的抛物线； （2）顶点为（0，1），经过点（3，-2）并且关于y 轴对称的抛物线． 【答案与解析】（1）由于待求抛物线形状相同，开口方向相反，可知二次项系数为，又顶点坐标是（0，-5），故常数项，所以所求抛物线为．（2）因为待求抛物线顶点为（0，1），所以其解析式可设为， 又∵ 该抛物线过点（3，-2），∴ ，解得．∴ 所求抛物线为．【总结升华】抛物线形状相同则相同，再由开口方向可确定的符号，由顶点坐标可确定的值，从而确定抛物线的解析式． 例2．在同一直角坐标系中，画出和的图象，并根据图象(如图所示)回答下列问题．2=++y ax bx c y m 2=++y ax bx c 2=+++y ax bx c m 2=++−y ax bx c m 2=++y ax bx c m 2=++y ax bx c 2()()=++++y a x m b x m c 2()()=−+−+y a x m b x m c =−+y x 2312=−+y x 231221=−k 5=−y x 2512=+y ax 12+=−a 912=−a 31=−+y x 3112a ||a k =+y ax k 2=−y x 2=−+y x 12(1)抛物线向________平移________个单位得到抛物线；(2)抛物线，开口方向是________，对称轴为________，顶点坐标为________；(3)抛物线，当x________时，随x 的增大而减小；当x________时，函数y 有最________值，其最________值是________．【答案】 (1)下； l ； (2)向下； y 轴； (0，1)； (3)＞0； ＝0； 大； 大 ； 1. 【解析】在同一平面直角坐标系内画出两条抛物线，利用图象回答问题．(1)抛物线向 下 平移 1__个单位得到抛物线；(2)抛物线，开口方向是 向下 ，对称轴为___ y 轴_____，顶点坐标为_ (0，1)__；(3)抛物线，当x ＞0时，y 随x 的增大而减小； 当x ＝0__时，函数y 有最 大 值，其最 大__值是 1 ．【总结升华】本例题把函数与函数的图象放在同一直角坐标系中进行对比，易得出二次函数与的图象形状相同，只是位置上下平移的结论．可以看作是把的图象向上或向下平移个单位得到的．例3. 有一个抛物线形的拱形隧道，隧道的最大高度为6m ，跨度为8m ，把它放在如图所示的平面直角坐标系中．（1）求这条抛物线所对应的函数关系式；（2）若要在隧道壁上点P （如图）安装一盏照明灯，灯离地面高4.5m ．求灯与点B 的距离．21y x =−+2y x =−21y x =−+21y x =−+21y x =−+2y x =−21y x =−+21y x =−+21y x =−+2y x =−2(0)y ax k a =+≠2(0)y ax a =≠2(0)y ax k a =+≠2(0)y ax a =≠(0)k >(0)k <||k【答案与解析】（1）由题意，设抛物线所对应的函数关系为y=ax2+6（a ＜0）， ∵点A （-4，0）或B （4，0）在抛物线上， ∴0=a•（-4）2+6， 16a+6=0，16a=-6，．故抛物线的函数关系式为.（2）过点P 作PQ ⊥AB 于Q ，连接PB ，则PQ=4.5m ．将y=4.5代入，得x=±2．∴P （-2，4.5），Q （-2，0）， 于是|PQ|=4.5，|BQ|=6，从而所以照明灯与点B 的距离为7.5m ．【总结升华】本题考查点的坐标的求法及二次函数的实际应用．此题为数学建模题，借助二次函数解决实际问题．（1）根据抛物线在坐标系的位置可设解析式：y=ax2+6，把点A （-4，0）代入即可；（2）灯离地面高4.5m ，即y=4.5时，求x 的值，再根据P 点坐标，勾股定理求PB 的值.38a =−2368y x =−+2368y x =−+7.5m =【变式】(1)抛物线的开口方向 ，对称轴是 ，顶点坐标是 ． (2)抛物线与的形状相同，其顶点坐标为（0，1），则其解析式为 ． (3)抛物线向 平移 个单位后，得到抛物线. 【答案】(1)下；y 轴；（0，-5）.(2)y=3x2+1, y=-3x2+1. (3)下；10.例4. 根据下列条件求a 的取值范围：(1)函数y ＝(a -2)x 2，当x ＞0时，y 随x 的增大而减小，当x ＜0时，y 随x 的增大而增大； (2)函数y ＝(3a -2)x 2有最大值； (3)抛物线y ＝(a+2)x 2与抛物线的形状相同； (4)函数的图象是开口向上的抛物线．【答案与解析】(1)由题意得，a-2＜0，解得a ＜2．(2)由题意得，3a-2＜0，解得．(3)由题意得，，解得，． (4)由题意得，，解得a1＝-2，a2＝1，但a ＞0，∴ a ＝1．【总结升华】解答此类问题，要注意联想二次函数的图象和性质，抓住形状、开口、最值、增减性等特征，并结合草图去确定二次项系数的取值范围．【变式】在同一平面直角坐标系中，一次函数与二次函数 的图象大致为（ ）．【答案】B.225y x =−−2y ax c =+23y x =2172y x =−+2132y x =−−212y x =−2a ay ax +=23a <1|2|2a +=−152a =−232a =−220a a a ⎧+=⎨>⎩y ax c =+2y ax c =+例5.在同一坐标系中，一次函数y=ax +b 与二次函数y=ax 2﹣b 的图象可能是（ ）A ．B ．C ．D ．【总结升华】先由一次函数y=ax+b 图象得到字母a 、b 的正负，再与二次函数y=ax2﹣b 的图象相比较看是否一致． 【答案】D. 【解析】解：A 、由直线y=ax+b 的图象经过第二、三、四象限可知：a ＜0，b ＜0， 二次函数y=ax2﹣b 的图象开口向上， ∴a ＞0，A 不正确；B 、由直线y=ax+b 的图象经过第一、二、三象限可知：a ＞0，b ＞0， 二次函数y=ax2﹣b 的图象开口向下， ∴a ＜0，B 不正确；C 、由直线y=ax+b 的图象经过第一、二、四象限可知：a ＜0，b ＞0， 二次函数y=ax2﹣b 的图象开口向上， ∴a ＞0，C 不正确；D 、由直线y=ax+b 的图象经过第一、二、三象限可知：a ＞0，b ＞0， 二次函数y=ax2﹣b 的图象开口向上，顶点在y 轴负半轴， ∴a ＞0，b ＞0，D 正确． 故选D ．【总结升华】本题考查了一次函数的图象以及二次函数的图象，解题的关键是根据函数图象逐条分析四个选项中a 、b 的正负．本题属于基础题，难度不大，解决该题型题目时，根据一次函数的图象找出其系数的正负，再与二次函数图象进行比较即可得出结论．题型二、二次函数2()(0)y a x h k a =−+≠图象及性质例6．二次函数y=﹣（x ﹣3）2+2的顶点的坐标是 ，对称轴是 ． 【思路点拨】根据二次函数顶点式解析式分别解答即可． 【答案】（3，2），直线x=3．【解析】二次函数y=﹣（x ﹣3）2+2；顶点坐标是（3，1），对称轴是直线x=3． 故答案为：（3，2），直线x=3．【总结升华】本题考查了二次函数的性质，熟练掌握利用二次函数顶点式形式求解对称轴和顶点坐标的方法是解题的关键．【变式】将抛物线向右平移2个单位，再向上平移5个单位，得到的抛物线解析式为 ．【答案】. 例7．将抛物线y=x 2﹣6x+5向上平移2个单位长度，再向右平移1个单位长度后，求得到的抛物线解析式.【答案与解析】解：y=x2﹣6x+5=（x ﹣3）2﹣4， ∴抛物线的顶点坐标为（3，﹣4），把点（3，﹣4）向上平移2个单位长度，再向右平移1个单位长度得到点的坐标为（4，﹣2）， ∴平移后得到的抛物线解析式为y=（x ﹣4）2﹣2．【总结升华】由于抛物线平移后的形状不变，故a 不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式． 【变式】二次函数的图象可以看作是二次函数的图象向 平移4个单位，再向 平移3个单位得到的．【答案】上；右.例8.已知是由抛物线向上平移2个单位长度，再向右平移1个单位长度得到的抛物线．(1)求出a 、h 、k 的值；(2)在同一坐标系中，画出与的图象； (3)观察的图象，当x 取何值时，y 随x 的增大而增大；当x 取何值时，y 随x 增大而减小，并求出函数的最值；23y x =−23127y x x =−+−21(3)42y x =−+212y x =2()y a x h k =−+212y x =−2()y a x h k =−+212y x =−2()y a x h k =−+(4)观察的图象，你能说出对于一切x 的值，函数y 的取值范围吗? 【答案与解析】(1)∵ 抛物线向上平移2个单位长度， 再向右平移1个单位长度得到的抛物线是，∴，1h =，．(2)函数与的图象如图所示．(3)观察的图象知，当时，y 随x 的增大而增大；当时，y 随x 增大而减小，当x ＝1时，函数y 有最大值是2． (4)由图象知，对于一切x 的值，总有函数值y ≤2．【总结升华】先根据平移的性质求出抛物线平移后的抛物线的解析式，再对比得到a 、h 、k 的值，然后画出图象，由图象回答问题．【变式】把二次函数的图象先向左平移2个单位，再向上平移4个单位，得到二次函数的图象．（1）试确定a 、h 、k 的值；（2）指出二次函数的开口方向，对称轴和顶点坐标，分析函数的增减性．2()y a x h k =−+212y x =−21(1)22y x =−−+12a =−2k =21(1)22y x =−−+212y x =−21(1)22y x =−−+1x <1x >212y x =−2()y a x h k =−+2()y a x h k =−+21(1)12y x =−+−2()y a x h k =−+【答案】（1）.（2）开口向下，对称轴x=1, 顶点坐标为（1，-5），当x ≥1时，y 随x 的增大而减小； 当x ＜1时，y 随x 的增大而增大.例9.二次函数y=（x ﹣1）2+1，当2≤y ＜5时，相应x 的取值范围为 ．【思路点拨】把y=2和y=5分别代入二次函数解析式，求x 的值，已知对称轴为x=1，根据对称性求x 的取值范围．【答案】﹣1＜x ≤0或2≤x ＜3． 【解析】解：当y=2时，（x ﹣1）2+1=2， 解得x=0或x=2，当y=5时，（x ﹣1）2+1=5，解得x=3或x=﹣1， 又抛物线对称轴为x=1， ∴﹣1＜x ≤0或2≤x ＜3．【总结升华】本题考查了二次函数的增减性，对称性．关键是求出函数值y=2或5时，对应的x 的值，再结合图象确定x 的取值范围．题型三、二次函数2()(0)y a x h k a =−+≠性质的综合应用例10．二次函数y 1=a （x ﹣2）2的图象与直线y 2交于A （0，﹣1），B （2，0）两点． （1）确定二次函数与直线AB（2）如图，分别确定当y 1＜y 2，y 1=y 2，y 1＞y 2时，自变量x 的取值范围．【答案与解析】解：（1）把A （0，﹣1）代入y1=a （x ﹣2）2，得：﹣1=4a ，即a=﹣， ∴二次函数解析式为y1=﹣（x ﹣2）2=﹣a2+a ﹣1； 设直线AB 解析式为y=kx+b ，1,1,52a h k =−==−把A （0，﹣1），B （2，0）代入得：，解得：k=，b=﹣1，则直线AB 解析式为y=x ﹣1；（2）根据图象得：当y1＜y2时，x 的范围为x ＜0或x ＞2；y1=y2时，x=0或x=2，y1＞y2时，0＜x ＜2． 【总结升华】可先由待定系数法建立方程组求出两个函数的解析式，然后利用函数图象写出自变量的取值范围．例11.在同一直角坐标系中，画出下列三条抛物线：，，．（1）观察三条抛物线的相互关系，并分别指出它们的开口方向、对称轴和顶点坐标； （2）请你说出抛物线的开口方向，对称轴及顶点坐标． 【答案与解析】 （1）列表：描点、连线，可得抛物线．将的图象分别向上和向下平移3个单位，就分别得到与的图象（如图所示）．抛物线，与开口都向上，对称轴都是y 轴，顶点坐标依次是（0，0）、（0，3）和（0，-3）．212y x =2132y x =+2132y x =−212y x c =+212y x =212y x=2132y x =+2132y x =−212y x =2132y x =+2132y x =−（2）抛物线的开口向上，对称轴是y 轴（或直线），顶点坐标为（0，c ）．【总结升华】先用描点法画出的图象，再用平移法得到另两条抛物线，并根据图象回答问题．规律总结：．例12.已知：二次函数y=x 2﹣4x+3．（1）求出该二次函数图象的对称轴和顶点坐标； （2）求出该抛物线与x 轴的交点坐标； （3）当x 取何值时，y ＜0． 【解析】解：（1）∵y=x2﹣4x+3， ∴y=（x ﹣2）2﹣1， ∴对称轴为：直线x=2， ∴顶点（2，﹣1）； （2）令y=0， 则，x2﹣4x+3=0， ∴（x ﹣1）（x ﹣3）=0， ∴x1=1，x2=3，∴与x 轴的交点坐标为（1，0），（3，0）； （3）当1＜x ＜3时，y ＜0．【总结升华】本题考查了二次函数的性质，抛物线与x 轴坐标的求解方法，二次函数与不等式，熟记性质并把函数解析式整理成顶点式形式求解更简便． 【变式】已知抛物线y=2（x ﹣1）2﹣8．（1）直接写出它的顶点坐标： ，对称轴： ； （2）x 取何值时，y 随x 增大而增大？ 【答案与解析】解：（1）抛物线y=2（x ﹣1）2﹣8的顶点坐标为（1，﹣8），对称轴为直线x=1； 故答案为（1，﹣8），直线x=1； （2）当x ＞1时，y 随x 增大而增大．212y x c =+0x =212y x=2y ax k =+k ←⎯⎯⎯⎯⎯向上平移个单位2y ax =k ⎯⎯⎯⎯→向下平移个单位2(0)y ax k k =−>例13. 如图所示，抛物线的顶点为C ，与y 轴交点为A ，过点A 作y 轴的垂线，交抛物线于另一点B ．(1)求直线AC 的解析式； (2)求△ABC 的面积；(3)当自变量x 满足什么条件时，有? 【答案与解析】(1)由知抛物线顶点C(-1，0)，令x ＝0，得， ∴ ．由待定系数法可求出，∴．(2)∵ 抛物线的对称轴为x ＝-1，根据抛物线对称性知． ∴ ．(3)根据图象知或时，有．【总结升华】 图象都经过A 点和C 点，说明A 点、C 点同时出现在两个图象上，A 、C 两点的坐标均满足两个函数的解析式，解答这类题时，要画出函数图象，结合几何图形的性质，运用数形结合的思想和抛物线的对称性，特别要慎重处理平面直角坐标系中的坐标(数)与线段长度(形)之间的关系，不要出现符号上的错误，充分利用函数图象弄清函数值与自变量的关系，利用图象比较函数值的大小，或根据函数值的大小，确定自变量的变化范围．【过关检测】一、单选题1．（2021秋·浙江绍兴·九年级校联考期中）二次函数22y x =−的顶点坐标是（ ） A ．（0，0）B ．（0，﹣2）C ．（0，2）D ．（，0）211)y x =+2y kx b =+12y y >211)y x =+y =A b =k =2y =+211)y x =+(B −122ABC S =⨯=△0x >1x <−12y y >【分析】直接2y ax k =+根据的性质求解即可．【详解】解：二次函数22y x =−的顶点坐标是（0，﹣2）．故选：B ．【点睛】本题考查了二次函数2y ax k =+ (a ，h ，k 为常数，a≠0)的性质，熟练掌握二次函数2y ax k =+的性质是解答本题的关键．2y ax k =+是抛物线的顶点式，a 决定抛物线的形状和开口方向，其顶点是(0，k)，对称轴是y 轴．2．（2023·浙江宁波·统考二模）已知点()11,A x y ，()22,B x y 是二次函数()233y x =−+上的两点，若123x x <<，126x x +>，则下列关系正确的是（ ）A ．123y y <<B ．123y y <<C ．213y y <<D ．213y y <<【答案】B【分析】根据二次函数的性质，进行分析即可得出结论． 【详解】解：∵()233y x =−+，对称轴为3x =，10a =>，∴抛物线的开口向上，当3x =时，函数取得最小值，3y =，抛物线上的点离对称轴越远，函数值越大， ∵123x x <<，126x x +>，∴点,A B 在对称轴的两侧，且1233x x −<−，∴123y y <<；故选B ．【点睛】本题考查二次函数的图象和性质．熟练掌握二次函数的性质，是解题的关键．3．（2022秋·浙江杭州·九年级校联考期中）对于二次函数()223y x =−+的图象，下列说法不正确的是（ ） A ．开口向下B ．对称轴是直线3x =−C ．顶点坐标为()30−，D ．当3x <−时，y 随x 的增大而减小【分析】根据二次函数的图象和性质，即可进行解答． 【详解】解：A 、∵20a =−<，∴函数图象开口向下，故A 正确，不符合题意； B 、对称轴是直线3x =−，故B 正确，不符合题意； C 、顶点坐标为()30−，，故C 正确，不符合题意；D 、∵函数图象开口向下，对称轴是直线3x =−，∴当3x <−时，y 随x 的增大而增大，故D 不正确，符合题意； 故选：D ．【点睛】本题主要考查了二次函数图象和性质，解题的关键是熟练掌握二次函数()2y a x h =−的顶点坐标为()0h ，，对称轴为x h =，当0a >时，函数图象开口向上，当a<0时，函数图象开口向下．4．（2022秋·浙江金华·九年级统考期中）已知()14.4,A y −，()23.3,B y −为抛物线()21y x =−+上的两点，则下列结论一定成立的是（ ） A ．210y y << B ．120y y <<C ．120y y <<D ．210y y <<【答案】C【分析】先判断抛物线的开口方向和对称轴位置，再根据增减性求解即可． 【详解】解：∵抛物线()21y x =−+的对称轴为直线=1x −，开口向下，顶点坐标为：()10−，，∴当1x <−时，y 随x 的增大而增大， 又∵ 4.4 3.31−<−<−， ∴120y y <<，故选 C ．【点睛】本题主要考查二次函数的性质，掌握二次函数的增减性是解题的关键．5．（2022秋·浙江杭州·九年级校考期中）设函数()112y x a =−，()222y x a =−，()323y x a =−．直线x b =的图象与函数1y ，2y ，3y 的图象分别交于点()1,A b c ，()2,B b c ，()3,C b c ，（ ） A ．若123b a a a <<<，则312c c c << B ．若123a b a a <<<，则123c c c << C ．若123a a b a <<<，则321c c c << D ．若123a a a b <<<，则321c c c << 【答案】D【分析】按照题意，画出满足题意的图象，根据直线x b =与二次函数图象的交点进行判断即可． 【详解】解：如图所示，A ．由图象可知，若123b a a a <<<，当x b =时，123c c c <<，故选项错误，不符合题意；B ．由图象可知，若123a b a a <<<，，当x b =时，123c c c <<不一定成立，故选项错误，不符合题意；C ．由图象可知，若123a a b a <<<，当x b =时，321c c c <<不一定成立，故选项错误，不符合题意；D ．由图象可知，若123a a a b<<<，当x b =时，321c c c <<，故选项正确，符合题意；故选：D【点睛】此题主要考查了二次函数的图象和性质，数形结合是解题的关键．6．（2023春·浙江绍兴·九年级校联考阶段练习）若二次函数2y 2(x 1)1=−−的图象如图所示，则坐标原点可能是（ ）A ．点AB ．点BC ．点CD ．点D【答案】A【分析】根据顶点坐标，进行判断即可．【详解】解：∵2y 2(x 1)1=−−，∴顶点坐标为：()1,1-，∴顶点坐标在第四象限， ∴原点在函数顶点的左上方， 由图可知，坐标原点只可能是点A ； 故选A ．【点睛】本题考查二次函数的性质及二次函数的图象，确定二次函数图象的顶点坐标是解题的关键．【答案】C【分析】根据题意分别画出12,y y 的图象，继而根据图象即可求解．【详解】解：∵直线1x =的图象与函数1y ，2y 的图象分别交于点()11,A c ，()21,B c ，A. 若121a a <<，如图所示，则12c c >B. 若121a a <<，如图所示，则12c c >则12c c <，故B 选项不合题意，C. 若121a a <<，如图所示，∴12c c <，故C 选项正确，D 选项不正确；故选：C ．【点睛】本题考查了二次函数图象的性质，数形结合是解题的关键．【答案】C【分析】根据各函数的增减性依次进行判断即可．【详解】解：A 、2(0)y x x =−>中，20k =−<，则当0x >时，y 随x 的增大而增大，即当12x x >时，必有12y y >，此时21210y y x x −>−，故本选项不成立；B 、∵2(2)5(0)y x x =−+≥的对称轴为直线2x =，∴当02x <<时，y 随x 的增大而减小，当2x >时y 随x 的增大而增大， ∴当2x >时，当12x x >时，必有12y y >，此时21210y y x x −>−，故本选项不成立；C 、∵2(3)4(0)y x x =−−<的对称轴为直线3x =，∴当3x <时，y 随x 的增大而减小， ∴当0x <时，当12x x >时，必有12y y <，此时21210y y x x −<−，故本选项成立；D 、∵37y x =+中，30k =>， ∴y 随x 的增大而增大，即当12x x >时，必有12y y >，此时21210y y x x −>−，故本选项不成立．故选：C ．【点睛】本题主要考查了一次函数、反比例函数和二次函数的图象和性质，掌握各类函数的增减性是关键．二、填空题【答案】a ＞2【分析】】根据二次函数的性质可知，当抛物线开口向下时，二次项系数2-a ＜0． 【详解】∵抛物线y=（2-a ）x2+2开口向下， ∴2-a ＜0，即a ＞2， 故答案为：a ＞2．【点睛】本题主要考查了二次函数的性质．用到的知识点：对于二次函数y=ax2+bx+c （a≠0）来说，当a ＞0时，抛物线y=ax2+bx+c （a≠0）开口向上；当a ＜0时，抛物线y=ax2+bx+c （a≠0）开口向下．10．（2022秋·浙江绍兴·九年级统考期中）二次函数()()232y x h t x t =−++≤≤+的图象上任意二点连线不与x 轴平行，则t 的取值范围为______．【答案】5t ≤−或3t ≥−【分析】先根据函数表达式得出函数的对称轴，再根据题意可得该二次函数的图象取对称轴的左边或对称轴的右边，即可进行解答． 【详解】解：∵二次函数表达式为()()232y x h t x t =−++≤≤+，∴该函数的对称轴为直线3x =−， ∵图象上任意二点连线不与x 轴平行， ∴3x ≤−或3x ≥−， ∵2t x t ≤≤+，∴233t t +≤−⎧⎨≥−⎩，解得：5t ≤−或3t ≥−． 故答案为：5t ≤−或3t ≥−．【点睛】本题主要考查了二次函数的图象和性质，解题的关键是熟练掌握二次函数的图象，会根据二次函数的表达式求出函数的对称轴．【答案】()2213y x =−−或()2213y x =−−−【分析】根据二次函数的顶点坐标为()1,3−，可得可设这个二次函数的解析式为()213y a x =−−，再根据图象的形状和与抛物线22y x =相同，可得2a =±，即可求解． 【详解】解：∵二次函数的顶点坐标为()1,3−，∴可设这个二次函数的解析式为()213y a x =−−，∵二次函数图象的形状与抛物线22y x =相同，， ∴2=a ，∴2a =±，∴这个二次函数的解析式为()2213y x =−−或()2213y x =−−−．故答案为：()2213y x =−−或()2213y x =−−−．【点睛】本题考查了二次函数的图象与性质，牢记形状相同的二次函数二次项系数的绝对值相等是解题的关键．12．（2022·浙江金华·九年级浙江省义乌市稠江中学校考阶段练习）如果一抛物线的对称轴为1x =，且经过点A （3,3），那么点A 关于对称轴的对称点B 的坐标为____________ 【答案】（-1,3）【分析】根据抛物线的对称性即可得到点B 的坐标． 【详解】解：∵抛物线的对称轴为1x =，点A （3,3）， ∴点A 关于对称轴的对称点B 的坐标为（-1,3）【点睛】本题主要考查二次函数图形的性质和特征，应用对称性性是解题的关键．13．（2022秋·浙江绍兴·九年级校考期中）已知点()11,A x y 、()22,B x y 为抛物线()22y x =−上的两点，如果122x x <<，那么1y ______2.(y 填“>”“<”或“=”)【答案】>【分析】根据函数的表达式即可得出该函数的对称轴和开口方向，根据对称轴和开口方向分析函数的增减性即可解答．【详解】解：抛物线表达式为：()22y x =−，∴函数开口向上，对称轴为2x =，∴当2x <时，y 随x 的增加而减小，2x >时，y 随x 的增大而增大， ∵122x x <<，∴12y y >，故答案为：>．【点睛】本题主要考查了二次函数的增减性，解题的关键是根据抛物表达式得出函数的开口方向和对称轴，从而分析函数的增减性．【答案】23(2)32y x =++【分析】根据二次函数的图象与性质即可得． 【详解】抛物线的顶点为(2,3)−∴可设此抛物线的解析式为2(2)3y a x =++又此抛物线的形状，开口方向与23312y x x =−+相同32a ∴=则此抛物线的解析式为23(2)32y x =++故答案为：23(2)32y x =++．【点睛】本题考查了二次函数的图象与性质，熟记二次函数的图象与性质是解题关键． 15．（2023秋·浙江湖州·九年级统考期末）抛物线22(3)4y x =−++的开口方向是______． 【答案】向下【分析】由函数解析式可得20a =−<，结合抛物线的性质即可得到答案； 【详解】解：由题意可得，∵22(3)4y x =−++，∴20a =−<， 故答案为：向下．【点睛】本题考查抛物线的性质：a<0开口向下，正确理解二次函数的性质是解题的关键．16．（2022秋·浙江杭州·九年级校考期中）已知二次函数()2y x a =−+，当4x ≤−时，y 随x 的增大而增大；当4x ≥−时，y 随x 的增大而减小，当0x =时，y 的值是______． 【答案】16−【分析】根据二次函数的增减性，结合图像与性质即可得到二次函数图像的对称轴为4x =−，从而确定a 值，得到二次函数解析式为()24y x =−+，将0x =代入即可得到结论．【详解】解：二次函数()2y x a =−+，当4x ≤−时，y 随x 的增大而增大；当4x ≥−时，y 随x 的增大而减小，4x a ∴=−=−，即4a =，∴二次函数解析式为()24y x =−+，当0x =时，()20416y =−+=−，故答案为：16−．【点睛】本题考查二次函数的图像与性质，熟练掌握二次函数增减性与对称轴的关系是解决问题的关键．17．（2020·浙江·模拟预测）无论a 取什么实数，点()21,241P a a a −−+都在二次函数y 上，(,)Q m n 是二次函数y 上的点，则2421m n −+=_____________． 【答案】3【分析】由题意可知y=2x2-1，首先把点Q （m ，n ）代入二次函数y=2x2-1解析式，代入得出，关于m ，n 的等式进一步整理得出答案即可．【详解】解：由题意得，当x=a-1时，y=2a2-4a+1=2（a-1）2-1， ∴可得：y=2x2-1，∵Q （m ，n ）是二次函数y=2x2-1上的点， ∴2m2-1=n ， ∴2m2-n=1，所以4m2-2n+1=2（2m2-n ）+1=3 故答案为：3．【点睛】此题考查二次函数图象上点的坐标特点，注意适合解析式的点在图象上，在图象上的点都适合二次函数．18．（2023春·浙江杭州·九年级校考阶段练习）已知二次函数2(1)10y x =−−+，当m x n ≤≤，且0mn <时，y 的最小值为2m ，y 的最大值2n ，则m n +的值为___________． 【答案】2【分析】由题意可得0m <，0n >，则y 的最小值为2m 为负数，最大值为2n 为正数．分两种情况讨论：①当1n <时，x m =时，y 取最小值，求出m 的值，当x n =时，y 取最大值，可求得n 的值，即可得到m n +的值；②当1n ≥时，当x m =时，y 取最小值，求出m 的值，当1x =时，y 取最大值，求出n 的值，或x n =时，y 取最小值，1x =时，y 取最大值，分别求出m ，n 的值，故可求解．【详解】解：二次函数2(1)10y x =−−+的大致图象如下：0mn <时，y 的最小值为2m ，y 的最大值为2n ，0m ∴<，0n >，①当1n <时，x m =时，y 取最小值，即()22110m m =−−+， 解得：3m =−．当x n =时，y 取最大值，即()22110n n =−−+， 解得：3n =或3(n =−均不合题意，舍去)；②当1n ≥时，当x m =时，y ()22110m m =−−+， 解得：3m =−．当1x =时，y 取最大值，即()221110n =−−+， 解得：5n =，或x n =时，y 取最小值，1x =时，y 取最大值，()22110m n =−−+，5n =，3m ∴=−，所以352m n +=−+=． 故答案为：2．【点睛】本题考查了二次函数的最值问题，二次函数的增减性，数形结合是解题的关键．三、解答题19．（2022秋·浙江丽水·九年级校联考期中）已知二次函数的图像以点()1,4A −为顶点，且过点()2,5B −． （1）求该函数的解析式；（2）直接写出y 随x 的增大而增大时自变量x 的取值范围．【答案】（1）223y x x =−−+；（2）1x <−【分析】（1）根据顶点坐标直接设解析式为顶点式，然后代入B 点坐标求解即可； （2）结合解析式，根据开口方向以及对称轴即可确定范围． 【详解】（1）设二次函数的解析式为()2y a x h k=−+．由题知：1h =−，4k =，则()214y a x =++，又∵二次函数图像过点()2,5B −∴()25214a −=++，∴1a =−．∴二次函数的解析式为：()221423y x x x =−++=−−+．（2）由（1）知当1x <−时，y 随x 的增大而增大．【点睛】灵活从二次函数三种形式中选择合适的表达式求解是解题关键．20．（2022·浙江·九年级专题练习）如图，已知经过原点的抛物线22y x mx =+与x 轴交于另一点A (2，0)．（1）求m 的值和抛物线顶点M 的坐标； （2）求直线AM 的解析式．【答案】（1）4m =−，M (1，-2)；（2）24y x =−【分析】（1）将A(2，0)代入抛物线的解析式，可求得m 的值，再配成顶点式即可求解； （2）利用待定系数法即可求得直线AM 的解析式．【详解】解 （1）∵抛物线22y x mx =+过点A(2，0)，22220m ∴⨯+=，解得4m =−，224y x x ∴=−，22(1)2x =−−,∴顶点M 的坐标是(1，-2)； （2）设直线AM 的解析式为()0y kx b k =+≠，∵图象过A(2，0)，M (1，-2)，202k b k b +=⎧∴⎨+=−⎩，解得24k b =⎧⎨=−⎩， ∴直线AM 的解析式为24y x =−．【点睛】本题考查了待定系数法求函数解析式，二次函数的图象和性质，解题的关键是灵活运用所学知识解决问题．【答案】(1)285S t t =++(2)25(3)S 有最小值-11【分析】（1）将x 和y 的表达式代入S 的表达式即可； （2）将2t =代入（1）中得到的函数表达式求解即可； （3）将（1）中的函数表达式化为顶点式即可解答．【详解】（1）解：将231x t y t −==+，代入8S x y =+得：()()2238185S t t t t =−++=++，∴S 与t 的函数关系式为：285S t t =++．（2）将2t =代入285S t t =++得：2282525S =+⨯+=，∴当2t =时25S =． （3）()2285411S t t t =++=+−，∴当4t =−时，函数S 有最小值-11．【点睛】本题主要考查了二次函数的性质，解题的关键是将函数表达式化为顶点式，得出函数的最值．【答案】（1）见解析；（2）见解析.【分析】（1）根据二次函数的图象解答即可； （2）从开口大小和增减性两个方面作答即可. 【详解】（1）解：如图：，2113=+y x 与2113=−−y x 图象的相同点是：形状都是抛物线，对称轴都是y 轴，2113=+y x 与2113=−−y x 图象的不同点是：2113=+y x 开口向上，顶点坐标是（0，1），2113=−−y x 开口向下，顶点坐标是（0，﹣1）；（2）解：两个函数图象的性质的相同点：开口程度相同，即开口大小一样；不同点：2113=+y x ，当x ＜0时，y 随x 的增大而减小，当x ＞0时，y 随x 的增大而增大；2113=−−y x ，当x ＜0时，y 随x 的增大而增大，当x ＞0时，y 随x 的增大而减小．【点睛】本题考查了二次函数的图象与性质，属于基础题型，熟练掌握抛物线的图象与性质是解答的关键. 23．（2020春·浙江杭州·八年级阶段练习）如图，已知二次函数的图象顶点是(2,3)P −，且过C 点(0,5)． （1）求此二次函数的解析式；（2）已知直线1y x =+与该二次函数图像相交于点,A B ，求,A B 两点的坐标． （3）写出当x 在什么范围内时，一次函数的值大于二次函数的值．【答案】（1）()2223y x =−−；（2）A （12，32），B （4，5）；（3）12＜x ＜4【分析】（1）根据顶点坐标设出顶点式，再将点C 坐标代入，即可求出解析式； （2）令()22231x x −−=+，解方程即可得到A 、B 的横坐标，从而计算出纵坐标；（3）根据图象可得出当一次函数图像在二次函数图像上方时的x 取值范围． 【详解】解：（1）∵二次函数的图象顶点是(2,3)P −， 设二次函数表达式为()223y a x =−−，∵过C 点(0,5)，代入，()20235a −−=，解得：a=2，∴二次函数表达式为：()2223y x =−−； （2）由题意可得：()22231x x −−=+，解得：x=12或4，。