特殊预测法:马尔可夫分析法
- 格式:doc
- 大小:25.00 KB
- 文档页数:2

第7节马尔可夫预测方法对事件的全面预测,不仅要能够指出事件发生的各种可能结果,而且还必须给出每一种结果出现的概率,说明被预测的事件在预测期内出现每一种结果的可能性程度。
这就是对于事件发生的概率预测。
马尔可夫(Markov)预测法,就是一种预测事件发生的概率的方法。
它是基于马尔可夫链,根据事件的目前状况预测其将来各个时刻(或时期)变动状况的一种预测方法。
马尔可夫预测法是对事件进行预测的基本方法,它是预测中常用的重要方法之一。
一、几个基本概念为了讨论马尔可夫预测法的应用,下面首先介绍几个基本概念。
(一) 状态、状态转移过程与马尔可夫过程(1) 状态。
在马尔可夫预测中,“状态”是一个重要的术语。
所谓状态,就是指某一事件在某个时刻(或时期)出现的某种结果。
一般而言,随着研究的事件及其预测的目标不同,状态可以有不同的划分方式。
例如,在商品销售预测中,有“畅销”、“一般”、“滞销”等状态;在农业收成预测中,有“丰收”、“平收”、“欠收”等状态;在人口构成预测中,有“婴儿”、“儿童”、“少年”、“青年”、“中年”、“老年”等状态;在经济发展水平预测中,有“落后”、“较发达”、“发达”等状态;在天气变化预测中,有“晴天”、“阴天”、“雨天”等状态;……;等等。
(2) 状态转移过程。
事件的发展,从一种状态转变为另一种状态,就称为状态转移。
譬如,天气变化从“晴天”转变为“阴天”,从“阴天”转变为“晴天”,从“晴天”转变为“晴天”,从“阴天”转变为“阴天”等都是状态转移。
(3) 马尔可夫过程。
在事件的发展过程中,若每次状态的转移都只仅与前一时刻的状态有关,而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔可夫过程。
许多事件发展过程的状态转移是具有无后效性的,对于这样一些事件发展过程,就可以用马尔可夫过程来描述。
(二) 状态转移概率与状态转移概率矩阵118119(1)状态转移概率。
在事件的发展变化过程中,从某一种状态出发,下一时刻转移到其它状态的可能性,称为状态转移概率。

马尔可夫分析法马尔可夫分析法是俄国数学家马尔可夫在1907年提出, 并由蒙特·卡罗加以发展而建立起的一种分析方法。
它主要用于分析随机事件未来发展变化的趋势, 即利用某一变量的现在状态和动向去预测该变量未来的状态及动向, 以便采取相应的对策。
1马尔可夫过程及马尔可夫链 [3]定义1设随机序列{X(n) ,n=0, 1, 2, …}的离散状态空间为E, 若对于任意m个非负整数n1,n2, …,nm(0≤n1<n2<…<nm) 和任意自然数k, 以及任意i1,i2, …,im,j∈E满足 [3]P{X(nm+k) =j|X(n1) =i1,X(n2) =i2, …,X(nm)=im}=P{X(nm+k) =j|X(nm) =im} (1) [3]则称X(n) ,n=0, 1, 2, …}为马尔可夫链。
[3]在式(1) 中, 如果nm表示现在时刻,n1,n2, …,nm-1表示过去时刻,nm+k表示将来时刻, 那么此式表明过程在将来nm+k时刻处于状态j仅依赖于现在nm时刻的状态im, 而与过去m-1个时刻n1,n2, …,nm-1所处的状态无关, 该特性称为马尔可夫性或无后效性。
式(1) 给出了无后效性的表达式。
[3]2齐次马尔可夫链和k步转移概率 [3]P{X(nm+k) =j|X(nm) =im},k≥1称之为马尔可夫链在n时刻的k 步转移概率, 记为Pij(n,n+k) 。
转移概率表示已知n时刻处于状态i, 经k个单位时间后处于状态j的概率。
若转移概率Pij(n,n+k) 是不依赖于n的马尔科夫链, 则称为齐次马尔可夫链。
这种状态只与转移出发状态i、转移步数k及转移到达状态j有关, 而与n无关。
此时,k 步转移概率可记为Pij(k) , 即 [3]Pij(k) =Pij(n,n+k) =P{X(n+k) =j|X(n) =i},k>0 (2) [3]式中,0≤Ρij(k)≤1,∑j∈EΡij(k)=10≤Ρij(k)≤1,∑j∈EΡij(k)=1。



马尔可夫预测法马尔可夫预测法是一种基于概率论的预测方法。
它通过分析系统的状态变化来预测未来的状态。
该方法适用于具有一定规律性的系统,并且可以用于各种领域,例如物理、经济、生物等。
下面将详细介绍马尔可夫预测法的原理和应用。
原理马尔可夫预测法是基于马尔可夫过程的。
马尔可夫过程是一个具有无记忆性的随机过程,即在给定当前状态的情况下,未来的状态只与当前状态有关,与过去的状态无关。
这个过程可以用一个状态转移矩阵来描述。
状态转移矩阵描述了从一个状态到另一个状态的概率,它的每个元素都代表了从一个状态到另一个状态的概率。
通过对状态转移矩阵的分析,可以预测系统在未来的状态。
应用马尔可夫预测法在各种领域都有广泛的应用。
在物理学中,它可以用于预测粒子的运动状态;在经济学中,它可以用于预测股市的走势;在生物学中,它可以用于预测疾病的传播。
下面将分别介绍这些应用。
物理学中的应用在物理学中,马尔可夫预测法可以用于预测粒子的运动状态。
例如,在原子的轨道运动中,电子的运动状态可以用一个状态向量来描述。
通过对状态向量的分析,可以预测电子在未来的位置。
经济学中的应用在经济学中,马尔可夫预测法可以用于预测股市的走势。
例如,在股市中,每一天的股价可以看作是一个状态。
通过对状态转移矩阵的分析,可以预测未来股价的走势。
这种方法已经被证明是一种有效的预测股市走势的方法。
生物学中的应用在生物学中,马尔可夫预测法可以用于预测疾病的传播。
例如,在流行病学中,每个人的健康状态可以看作是一个状态。
通过对状态转移矩阵的分析,可以预测疾病的传播。
这种方法已经被证明是一种有效的预测疾病传播的方法。
总结马尔可夫预测法是一种基于概率论的预测方法。
它通过分析系统的状态变化来预测未来的状态。
该方法适用于具有一定规律性的系统,并且可以用于各种领域。
在物理、经济、生物等领域中,马尔可夫预测法已经成为一种重要的预测方法。


特殊预测法:马尔可夫分析法定义:马尔可夫分析法是应用俄国数学家马尔可夫发现系统状态概率转移过程规律的数学方程,通过分析随机变量的现时变化情况,预测这些变量未来变化趋势及可能结果,为决策者提供决策信息的一种分析方法。
•单个生产厂家的产品在同类商品总额中所占的比率,称为该厂产品的市场占有率。
在激烈的竞争中,市场占有率随产品的质量、消费者的偏好以及企业的促销作用等因素而发生变化,企业在对产品种类与经营方向做出决策时,需要预测各种商品之间不断转移的市场占有率。
•市场占有率的预测可采用马尔可夫分析法,也就是运用转移概率矩阵对市场占有率进行市场趋势分析的方法。
俄国数学家马尔可夫在20世纪初发现:一个系统的某些因素在转移中,第N次结果只受第N-1次结果影响,只与当前所处状态有关,与其他无关。
例如:研究一个商店的累计销售额,如果现在时刻的累计销售额已知,则未来某一时刻的累计销售额与现在时刻以前的任一时刻的累计销售额都无关。
•在马尔可夫分析中,引入状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态;状态转移是指客观事物由一种状态转移到另一种状态的概率。
•马尔可夫分析法的一般步骤为:•1、调查目前的市场占有率情况;•2、调查消费者购买产品时的变动情况;•3、建立数学模型;•【•4、预测未来市场的占有率。
例一:一个800户居民点,提供服务的A、B、C三家副食品店,从产品、服务等方面展开竞争,各自原有稳定的居民户购买者开始出现了变化。
经过调查获得上月与本月三家商店的居民资料如表1;两个月中三商店都失去一些客户,同时也都赢得了一些客户,其转移变化资料如表2。
用马尔科夫法预测稳定状态下三商店的市场占有率。
表1表2例二:假定某小区有1000户居民,每户居民每月用一块香皂,并且只购买A牌、B牌、C牌。
8月份使用A牌香皂居民有500户,使用B 牌居民有200户,使用C牌居民有300户。
据调查9月份使用A牌香皂仍在使用的有360户,50户表示要改买B牌,90户表示要改买C牌;在使用B牌的用户中,120户仍在使用B牌,表示改买A牌的有40户,改买C牌的有40户;在使用C牌的用户中,表示仍在使用的有230户,有30户表示改买A牌,有40户表示改买C牌。
马尔可夫(Markov)分析法范例
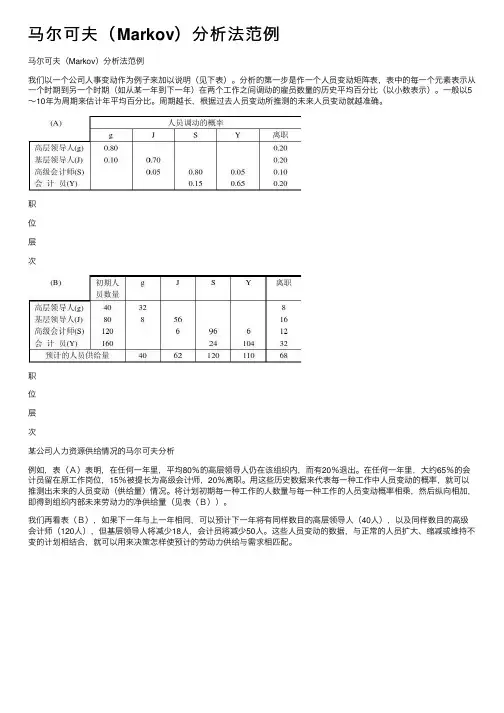
马尔可夫(Markov)分析法范例
我们以⼀个公司⼈事变动作为例⼦来加以说明(见下表)。
分析的第⼀步是作⼀个⼈员变动矩阵表,表中的每⼀个元素表⽰从⼀个时期到另⼀个时期(如从某⼀年到下⼀年)在两个⼯作之间调动的雇员数量的历史平均百分⽐(以⼩数表⽰)。
⼀般以5~10年为周期来估计年平均百分⽐。
周期越长,根据过去⼈员变动所推测的未来⼈员变动就越准确。
职
位
层
次
职
位
层
次
某公司⼈⼒资源供给情况的马尔可夫分析
例如,表(A)表明,在任何⼀年⾥,平均80%的⾼层领导⼈仍在该组织内,⽽有20%退出。
在任何⼀年⾥,⼤约65%的会计员留在原⼯作岗位,15%被提长为⾼级会计师,20%离职。
⽤这些历史数据来代表每⼀种⼯作中⼈员变动的概率,就可以推测出未来的⼈员变动(供给量)情况。
将计划初期每⼀种⼯作的⼈数量与每⼀种⼯作的⼈员变动概率相乘,然后纵向相加,即得到组织内部未来劳动⼒的净供给量(见表(B))。
我们再看表(B),如果下⼀年与上⼀年相同,可以预计下⼀年将有同样数⽬的⾼层领导⼈(40⼈),以及同样数⽬的⾼级会计师(120⼈),但基层领导⼈将减少18⼈,会计员将减少50⼈。
这些⼈员变动的数据,与正常的⼈员扩⼤、缩减或维持不变的计划相结合,就可以⽤来决策怎样使预计的劳动⼒供给与需求相匹配。

马尔可夫预测算法综述马尔可夫预测法以系统状态转移图为分析对象,对服从给定状态转移率、系统的离散稳定状态或连续时间变化状态进行分析马尔可夫预测技术是应用马尔可夫链的基本原理和方法研究分析时间序列的变化规律,并预测其未来变化趋势的一种技术。
方法由来马尔可夫是俄国的一位著名数学家 (1856—1922),20世纪初,他在研究中发现自然界中有一类事物的变化过程仅与事物的近期状况有关,而与事物的过去状态无关。
针对这种情况,他提出了马尔可夫预测方法,该方法具有较高的科学性,准确性和适应性,在现代预测方法中占有重要地位。
基础理论在自然界和人类社会中,事物的变化过程可分为两类:一类是确定性变化过程;另一类是不确定性变化过程。
确定性变化过程是指事物的变化是由时间唯一确定的,或者说,对给定的时间,人们事先能够确切地知道事物变化的结果。
因此,变化过程可用时间的函数来描述。
不确定性变化过程是指对给定的时间,事物变化的结果不止一个,事先人们不能肯定哪个结果一定发生,即事物的变化具有随机性。
这样的变化过程称为随机过程一个随机试验的结果有多种可能性,在数学上用一个随机变量(或随机向量)来描述。
在许多情况下,人们不仅需要对随机现象进行一次观测,而且要进行多次,甚至接连不断地观测它的变化过程。
这就要研究无限多个,即一族随机变量。
随机过程理论就是研究随机现象变化过程的概率规律性的。
客观事物的状态不是固定不变的,它可能处于这种状态,也可能处于那种状态,往往条件变化,状态也会发生变化状态即为客观事物可能出现或存在的状况,用状态变量表示状态:⎪⎪⎭⎫⎝⎛⋅⋅⋅=⋅⋅⋅==,2,1,,2,1t N i i X t 它表示随机运动系统,在时刻),2,1( =t t 所处的状态为),2,1(N i i =。
状态转移:客观事物由一种状态到另一种状态的变化。
设客观事物有N E E E E ...,,321共 N 种状态,其中每次只能处于一种状态,则每一状态都具有N 个转向(包括转向自身),即由于状态转移是随机的,因此,必须用概率来描述状态转移可能性的大小,将这种转移的可能性用概率描述,就是状态转移概率。

案例九-马尔科夫预测案例九 马尔科夫预测一、 市场占有率的预测重点例1:在北京地区销售鲜牛奶主要由三个厂家提供。
分别用1,2,3表示。
去年12月份对2000名消费者进行调查。
购买厂家1,2和3产品的消费者分别为800,600和600。
同时得到转移频率矩阵为:3202402403601806036060180N ⎛⎫ ⎪= ⎪ ⎪⎝⎭其中第一行表示,在12月份购买厂家1产品的800个消费者中,有320名消费者继续购买厂家1的 产品。
转向购买厂家2和3产品的消费者都是240人。
N 的第二行与第三行的含义同第一行。
(1) 试对三个厂家1~7月份的市场占有率进行预测。
(2) 试求均衡状态时,各厂家的市场占有率。
解:(1)用800,600和600分别除以2000,得到去年12月份各厂家的市场占有率,即初始分布0(0.4,0.3,0.3)p =。
用800,600和600分别去除矩阵N 的第一行、第二行和第三行的各元素,得状态转移矩阵:0.40.30.30.60.30.10.60.10.3P ⎛⎫ ⎪= ⎪ ⎪⎝⎭于是,第k 月的绝对分布,或第 月的市场占有率为:00()(1,2,3,,7)k k P p P k p P =⋅=1k =时,()()10.40.30.30.40.30.30.60.30.10.520.240.240.60.10.3p ⎛⎫⎪== ⎪ ⎪⎝⎭2k =时,()()()220.40.30.30.520.240.240.4960.2520.252p P P ===3k =时,()()()330.40.30.30.4960.2520.2520.50080.24960.2496p P P === 类似的可以计算出4p ,5p ,6p 和7p 。
现将计算结果绘制成市场占有率变动表,如表所示:从表中可以看到,厂家1的市场占有率随时间的推移逐渐稳定在50%,而厂家2和厂家3的市场占有率随都逐渐稳定在25%.由于转移概率矩阵P 是正规矩阵,因此P 有唯一的均衡点μ。

马尔可夫预测方法1马尔可夫预测的性质及运用对事件的全面预测,不仅要能够指出事件发生的各种可能结果,而且还必须给出每一种结果出现的概率,说明被预测的事件在预测期内出现每一种结果的可能性程度。
这就是关于事件发生的概率预测。
马尔可夫(Markov)预测法,就是一种关于事件发生的概率预测方法。
它是根据事件的目前状况来预测其将来各个时刻(或时期)变动状况的一种预测方法。
马尔可夫预测法是地理预测研究中重要的预测方法之一。
2基本概念(一)状态、状态转移过程与马尔可夫过程1.状态 在马尔可夫预测中,“状态”是一个重要的术语。
所谓状态,就是指某一事件在某个时刻(或时期)出现的某种结果。
一般而言,随着所研究的事件及其预测的目标不同,状态可以有不同的划分方式。
譬如,在商品销售预测中,有“畅销”、“一般”、“滞销”等状态;在农业收成预测中,有“丰收”、“平收”、“欠收”等状态;在人口构成预测中,有“婴儿”、“儿童”、“少年”、“青年”、“中年”、“老年”等状态;等等。
2.状态转移过程 在事件的发展过程中,从一种状态转变为另一种状态,就称为状态转移。
事件的发展,随着时间的变化而变化所作的状态转移,或者说状态转移与时间的关系,就称为状态转移过程,简称过程。
3.马尔可夫过程 若每次状态的转移都只仅与前一时刻的状态有关、而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔可夫过程。
在区域开发活动中,许多事件发展过程中的状态转移都是具有无后效性的,对于这些事件的发展过程,都可以用马尔可夫过程来描述。
(二)状态转移概率与状态转移概率矩阵1.状态转移概率 在事件的发展变化过程中,从某一种状态出发,下一时刻转移到其它状态的可能性,称为状态转移概率。
根据条件概率的定义,由状态E i 转为状态E j 的状态转移概率P (E i →E j )就是条件概率P (E j /E i ),即P(Ei Ej)=P(Ej/Ei)=Pij → (1)2.状态转移概率矩阵 假定某一种被预测的事件有E 1,E 2,…,E n ,共n 个可能的状态。
为什么HR可以⽤马尔科夫法预测未来⼈⼒供给?
马尔可夫分析法⼜称为马尔可夫转移矩阵法,是指在马尔可夫过程的假设前提下,通过分析随
机变量的现时变化情况来预测这些变量未来变化情况的⼀种预测⽅法。
马尔科夫法实际上已经
可以运⽤到很多经济学之外科学领域。
⽐如我们可以使⽤马尔科夫法分析未来的⼈才供给的变
化。
⼈⼒资源使⽤模版:
注意事项:
1 马尔科夫分析法预测的前提之⼀是趋势变化和发展具有持续性和稳定性。
在实际使⽤中,需要
依据客观情况对预测结果进⾏再次预判(⽐如战略变化/市场政策变化/组织架构变动等等)
2 马尔科夫分析法预测的前提之⼆是要有准确的历史数据作为预测的基础。
也突显出⽇常HR管
理基础⼯作的重要性
3 马尔科夫分析法预测的前提之三是要有相对固定的时间周期。
若历史数据的统计周期和推算的
周期有差异,则推算结果的准确性也就有了偏差。
在生物信息学中,利用马尔可夫模型进行基因序列分析是一种常见的方法。
马尔可夫模型是一种数学工具,用于描述随机过程中状态之间的转移规律。
在基因序列分析中,马尔可夫模型可以帮助我们理解基因序列中的潜在规律和模式,从而揭示基因在生物学功能和进化中的作用。
本文将介绍如何利用马尔可夫模型进行基因序列分析,包括模型的建立和参数估计等内容。
首先,我们需要了解马尔可夫模型的基本原理。
马尔可夫模型是一种描述状态转移的数学模型,其中状态之间的转移是根据一定的概率分布进行的。
在基因序列分析中,我们可以将基因序列看作是一个由不同碱基(A、T、C、G)组成的状态序列,而碱基之间的转移则可以看作是状态之间的转移。
通过建立马尔可夫模型,我们可以推断出碱基之间的转移规律,从而揭示基因序列中的潜在模式和规律。
接下来,我们将介绍如何建立马尔可夫模型进行基因序列分析。
首先,我们需要选择一个适当的阶数来描述基因序列的转移规律。
在实际应用中,通常选择一阶或二阶马尔可夫模型来描述基因序列的转移规律。
一阶马尔可夫模型假设当前状态的转移只与上一个状态有关,而二阶马尔可夫模型则考虑了当前状态的转移与前两个状态有关。
根据实际情况和需要,我们可以选择适当的阶数来建立马尔可夫模型。
其次,我们需要估计马尔可夫模型的参数。
在基因序列分析中,我们通常使用极大似然估计法来估计马尔可夫模型的参数。
极大似然估计法通过最大化观测数据的似然函数来估计模型的参数,从而得到最优的参数估计。
通过参数估计,我们可以得到马尔可夫模型的转移概率矩阵,从而揭示基因序列中的转移规律。
最后,我们可以利用建立好的马尔可夫模型进行基因序列分析。
通过模型的转移概率矩阵,我们可以对基因序列进行状态转移的预测和分析。
例如,我们可以利用马尔可夫模型预测基因序列的状态转移路径,从而揭示基因序列中的重要模式和规律。
通过基因序列分析,我们可以更好地理解基因的功能和进化,为生物学研究提供重要的参考和支持。
马尔可夫预测方法1马尔可夫预测的性质及运用对事件的全面预测,不仅要能够指出事件发生的各种可能结果,而且还必须给出每一种结果出现的概率,说明被预测的事件在预测期内出现每一种结果的可能性程度。
这就是关于事件发生的概率预测。
马尔可夫(Markov)预测法,就是一种关于事件发生的概率预测方法。
它是根据事件的目前状况来预测其将来各个时刻(或时期)变动状况的一种预测方法。
马尔可夫预测法是地理预测研究中重要的预测方法之一。
2基本概念(一)状态、状态转移过程与马尔可夫过程1.状态 在马尔可夫预测中,“状态”是一个重要的术语。
所谓状态,就是指某一事件在某个时刻(或时期)出现的某种结果。
一般而言,随着所研究的事件及其预测的目标不同,状态可以有不同的划分方式。
譬如,在商品销售预测中,有“畅销”、“一般”、“滞销”等状态;在农业收成预测中,有“丰收”、“平收”、“欠收”等状态;在人口构成预测中,有“婴儿”、“儿童”、“少年”、“青年”、“中年”、“老年”等状态;等等。
2.状态转移过程 在事件的发展过程中,从一种状态转变为另一种状态,就称为状态转移。
事件的发展,随着时间的变化而变化所作的状态转移,或者说状态转移与时间的关系,就称为状态转移过程,简称过程。
3.马尔可夫过程 若每次状态的转移都只仅与前一时刻的状态有关、而与过去的状态无关,或者说状态转移过程是无后效性的,则这样的状态转移过程就称为马尔可夫过程。
在区域开发活动中,许多事件发展过程中的状态转移都是具有无后效性的,对于这些事件的发展过程,都可以用马尔可夫过程来描述。
(二)状态转移概率与状态转移概率矩阵1.状态转移概率 在事件的发展变化过程中,从某一种状态出发,下一时刻转移到其它状态的可能性,称为状态转移概率。
根据条件概率的定义,由状态E i 转为状态E j 的状态转移概率P (E i →E j )就是条件概率P (E j /E i ),即 P(Ei Ej)=P(Ej/Ei)=Pij → (1)2.状态转移概率矩阵 假定某一种被预测的事件有E 1,E 2,…,E n ,共n 个可能的状态。
特殊预测法:马尔可夫分析法
定义:马尔可夫分析法是应用俄国数学家马尔可夫发现系统状态概率转移过程规律的数学方程,通过分析随机变量的现时变化情况,预测这些变量未来变化趋势及可能结果,为决策者提供决策信息的一种分析方法。
•单个生产厂家的产品在同类商品总额中所占的比率,称为该厂产品的市场占有率。
在激烈的竞争中,市场占有率随产品的质量、消费者的偏好以及企业的促销作用等因素而发生变化,企业在对产品种类与经营方向做出决策时,需要预测各种商品之间不断转移的市场占有率。
•市场占有率的预测可采用马尔可夫分析法,也就是运用转移概率矩阵对市场占有率进行市场趋势分析的方法。
俄国数学家马尔可夫在20世纪初发现:一个系统的某些因素在转移中,第N次结果只受第N-1次结果影响,只与当前所处状态有关,与其他无关。
例如:研究一个商店的累计销售额,如果现在时刻的累计销售额已知,则未来某一时刻的累计销售额与现在时刻以前的任一时刻的累计销售额都无关。
•在马尔可夫分析中,引入状态转移这个概念。
所谓状态是指客观事物可能出现或存在的状态;状态转移是指客观事物由一种状态转移到另一种状态的概率。
•马尔可夫分析法的一般步骤为:
•1、调查目前的市场占有率情况;
•2、调查消费者购买产品时的变动情况;
•3、建立数学模型;
•4、预测未来市场的占有率。
例一:一个800户居民点,提供服务的A、B、C三家副食品店,从产品、服务等方面展开竞争,各自原有稳定的居民户购买者开始出现了变化。
经过调查获得上月与本月三家商店的居民资料如表1;两个月中三商店都失去一些客户,同时也都赢得了一些客户,其转移变化资料如表2。
用马尔科夫法预测稳定状态下三商店的市场占有率。
表1
表2
例二:假定某小区有1000户居民,每户居民每月用一块香皂,并且只购买A牌、B牌、C牌。
8月份使用A牌香皂居民有500户,使用B 牌居民有200户,使用C牌居民有300户。
据调查9月份使用A牌香皂仍在使用的有360户,50户表示要改买B牌,90户表示要改买C牌;在使用B牌的用户中,120户仍在使用B牌,表示改买A牌的有40户,改买C牌的有40户;在使用C牌的用户中,表示仍在使用的有230户,有30户表示改买A牌,有40户表示改买C牌。
请用马尔科夫预测法预测10月份及稳定状态下三种品牌香皂在此小区的市场占有率各是多少?。