下载文档原格式
循环伏安法原理：循环伏安法（CV）是最重要的电分析化学研究方法之一。
该方法使用的仪器简单，操作方便，图谱解析直观，在电化学、无机化学、有机化学、生物化学等许多研究领域被广泛应用。
循环伏安法通常采用三电极系统，一支工作电极（被研究物质起反应的电极），一支参比电极（监测工作电极的电势），一支辅助（对）电极。
外加电压加在工作电极与辅助电极之间，反应电流通过工作电极与辅助电极。
对可逆电极过程（电荷交换速度很快），如一定条件下的Fe(CN)63-/4-氧化还原体系，当电压负向扫描时，Fe(CN)63－在电极上还原，反应为：Fe(CN)63－＋e-→Fe(CN)64－得到一个还原电流峰。
当电压正向扫描时，Fe(CN)64－在电极上氧化，反应为：Fe(CN)64－－e-→Fe(CN)63－得到一个氧化电流峰。
所以，电压完成一次循环扫描后，将记录出一个如图2所示的氧化还原曲线。
扫描电压呈等腰三角形。
如果前半部扫描(电压上升部分)为去极化剂在电极上被还原的阴极过程，则后半部扫描(电压下降部分)为还原产物重新被氧化的阳极过程。
因此．一次三角波扫描完成一个还原过程和氧化过程的循环，故称为循环伏安法。
应用领域：循环伏安法能迅速提供电活性物质电极反应的可逆性，化学反应历程，电活性物质的吸附等许多信息。
循环伏安法可用于研究化合物电极过程的机理、双电层、吸附现象和电极反应动力学．成为最有用的电化学方法之一。
如通过对未知研究体系的CV研究，可以获研究对象的反应电位或和平衡电位, 估算反应物种的量，以及判断反应的可逆性。
电化学反应中物种反应的量可以依据Faraday定律估算，, 其中m为反应的摩尔量, n为电极反应中的得失电子数，F为图2 氧化还原cv曲线图图1 cv图中电势~时间关系图3 Ag在Pt电极上电结晶过程的CV图0.01mol/LagNO3+0.1mol/LKNO3Faraday常数（96485 C.molmnFidtQt==∫0-1）。
线性扫描伏安法测定水样中的微量铜1、实验目的（1）了解线性扫描伏安法测定的基本原理和方法；（2）学习相关伏安仪的使用方法；（3）学习和掌握标准加入法；2、实验原理与经典极谱法不同，线性扫描伏安法将一锯齿形脉冲电压加在电解池的工作电极上，电压扫描速度比经典极谱法快得多，一般为每秒几十到几百毫伏。
由于电压扫描速度特别快，当达到待测物质析出的电位时，该物质在电极上迅速还原，产生很大的电流。
随后，电位继续变负，电极表面待测物质浓度迅速降低，由于电解时间的增加，扩散层厚度迅速增大，从而导致电流迅速下降，电流～电压关系呈现峰形。
当底液及其它条件一定时，其峰电位E p与被测物的性质及底液有关，而其峰电流i p则与被测物质浓度呈线性关系：i p=Kc据此可进行定量分析。
本实验采用标准加入法，测定水样中微量铜的含量，即在未知浓度的含铜水样中，先加入一定浓度的NaNO3作为支持电解质，测量其峰电流，然后逐次加入一定浓度的标准铜，每加入一次铜测量一次峰电流，最后用峰电流对标准铜的浓度作图，得一直线，它的外延线与浓度轴的交点即为水样中铜的含量。
3、仪器与药品XJP-821(C)型新极谱仪；ATA－1B型旋转圆盘电极，ZF-10B数据采集存贮器；工作电极：玻碳电极；参比电极：饱和甘汞电极；辅助电极：Pt电极。
100微升微量移液器，10毫升量筒，5毫升移液管，电解池；Cu2+标准贮备液：准确配制1.00mg·mL-1的Cu2+标准贮备液；支持电解质溶液：1.0 mol·L-1 NaNO3+1.0 mol·L-1HNO3溶液；待测水样。
4、实验步骤1)将三根电极的导线分别与圆盘电极上的各电极连接，新极谱仪的输出连线与数据采集存贮器相联；2)参见新极谱仪面板示意图，熟悉仪器；3)将仪器开关（后面板上）置开，预热仪器10分钟；4)调节仪器参数：调节扫描速度14，使其为100mV/s，调节扫描上限4，使其为-500mV，调节扫描下限6，使其为+500mV，调节扫描起始5，使其为+500mV；将面板上各开关及旋钮设置如下：3置于“循环”，18置于“大电流量程”，17置于“50μA”，9置于“i-E”，11置于“断”。
lsv线性扫描伏安曲线
什么是线性扫描伏安曲线？
线性扫描伏安曲线（Linear Scanning Voltammetry）是一种采用恒定电压扫描幅度来测量起始电压下物质的电位活性的实验方法。
它可以准确检测到反应型材料的电化学变化，以获得丰富的信息，例如还原机理以及电子转移速率等。
线性扫描伏安曲线的优点：
1.非常灵敏：线性扫描伏安曲线具有非常灵敏的检测和测量能力，可以检测出含有低浓度的电化学反应产物；
2.快速：线性扫描伏安曲线可以在几秒钟至几分钟的时间内完成测量，比其他类似电化学技术更快；
3.易操作：线性扫描伏安曲线操作简单，在获取有效信息的同时可以大大减少所需的技术复杂度；
4.宽广的应用范围：线性扫描伏安曲线能够同时测量相对稳定的电化学反应，以及单次活化能较高或较小的电化学反应，因而应用范围较为宽广。
线性扫描伏安曲线的应用：
1.测量福克斯正极反应：线性扫描伏安曲线本身能检测到福克斯正极反应，但也可以将其与其他电化学技术相结合以获得更精确的测量结果；
2.用于药物研究：线性扫描伏安曲线可以用于药物有效性研究，以及药物输出和药物代谢过程的定量研究；
3.测量生物化学反应：线性扫描伏安曲线可以用于生物样品中的酶反应，DNA、RNA和蛋白质的电化学检测，实现快速、灵敏的检测分析；
4.用于电池组研究：线性扫描伏安曲线可以用于电池组的测试和性能分析，从而提高全球能源使用的效率。
总结：
线性扫描伏安曲线是一种恒定电压扫描测量电位活性的实验方法，具有非常灵敏的检测和测量能力，且它操作简单，快速，宽广的应用范围，可以应用于福克斯正极反应、药物研究、生物样品的酶反应、DNA、RNA和蛋白质的电化学检测、电池组研究等领域。
电化学测试锂离子电池稳态测量技术-线性电势扫描伏安法
（LSVCV）
锂离子电池电极材料在电池充放电过程中一般经历以下几个步骤：①溶剂化的锂离子从电解液内迁移到电解液/固体电极的两相界面；②溶剂化的锂离子吸附在电解液/固体电极的两相界面；③去溶剂化；④电荷转移，电子注入电极材料的导带，吸附态的锂离子从电解液相迁移至活性材料表面晶格；⑤锂离子从活性材料表面晶格向内部扩散或迁移；⑥电子从集流体向活性材料的迁移。
线性电势扫描法在电化学测量中有着广泛的应用，常用于：①判断电极体系中可能发生的电化学反应；②判断电极过程的可逆性；③判断电极反应的反应物来源；
④研究电极活性物质的吸脱附过程。
锂离子电池基础科学问题（Ⅻ Ⅰ）——电化学测量方法. 凌仕刚，吴娇杨，张舒，高健，王少飞，李泓.
Das S R，Majumder S B，Katiyar R S. Kinetic analysis of the Li ionintercalation behavior of solution derived nano-crystalline lithiummanganate thin films[J]. Journal of Power Sources，2005，139：261-268.
Tang S B，Lai M O，Lu L. Li-ion diffusion in highly (003) oriented LiCoO2 thin film cathode prepared by pulsed laser deposition[J]. Journal of Alloys and Compounds，2008，449（1-2）：300-303.。
循环伏安法原理：循环伏安法（CV ）是最重要的电分析化学研究方法之一。
该方法使用的仪器简单，操作方便，图谱解析直观，在电化学、无机化学、有机化学、生物化学等许多 研究领域被广泛应用。
循环伏安法通常采用三电极系统，一支工作电极（被研究物质起反应的电极），一支参比电极（监测工作电极的电势），一支辅助（对）电极。
外加电压加在工作电极与辅助电极之间，反应电流通过工作电极与辅助电极。
对可逆电极过程（电荷交换速度很快），如一定条件下的Fe(CN)63-/4-氧化还原体系，当电压负向扫描时，Fe(CN)63－ 在电极上还原，反应为：Fe(CN)63－＋e - → Fe(CN)64－得到一个还原电流峰。
当电压正向扫描时，Fe(CN)64－在电极上氧化，反应为： Fe(CN)64－ － e - → Fe(CN)63－得到一个氧化电流峰。
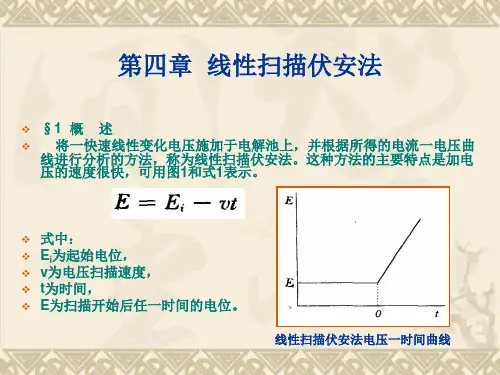
所以，电压完成一次循环扫描后，将记录出一个如图2所示的氧化还原曲线。
扫描电压呈等腰三角形。
如果前半部扫描(电压上升部分)为去极化剂在电极上被还原的阴极过程，则后半部扫描(电压下降部分)为还原产物重新被氧化的阳极过程。
因此．一次三角波扫描完成一个还原过程和氧化过程的循环，故称为循环伏安法。
应用领域：循环伏安法能迅速提供电活性物质电极反应的可逆性，化学反应历程，电活性物质的吸附等许多信息。
循环伏安法可用于研究化合物电极过程的机理、双电层、吸附现象和电极反应动力学．成为最有用的电化学方法之一。
如通过对未知研究体系的CV 研究，可以获研究对象的反应电位或和平衡电位, 估算反应物种的量，以及判断反应的可逆性。
电化学反应中物种反应的量可以依据Faraday 定律估算，, 其中m 为反应的摩尔量, n 为电极反应中的得失电子数，F 为 图2 氧化还原cv 曲线图图1 cv 图中电势~时间关系图3 Ag在Pt电极上电结晶过程的CV图0.01mol/LagNO3+0.1mol/LKNO3Faraday常数（96485 C.molmnFidtQt==∫0-1）。
