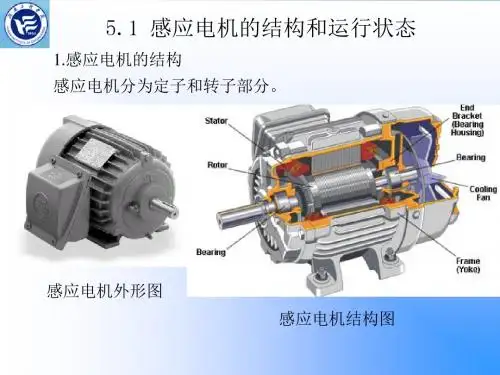
感应电动机的转矩-转差率曲线

电机iq曲线
电机的iq曲线，也称为电机的电流-转矩曲线，是描述电机在不同电流（I）和转矩（Tq）下的性能表现。

这个曲线图通常用于展示电机在控制过程中的动态性能，特别是在矢量控制或场向量控制中。

在iq曲线图中，横轴通常表示d轴电流（Id），纵轴表示q 轴电流（Iq）。

d轴和q轴是电机控制中的两个重要参数，分别代表电机的磁场和电枢电流分量。

通过调整这两个电流分量，可以控制电机的转矩和转速。

在iq曲线图中，不同的曲线可能代表不同的运行状态或控制策略。

例如，一些曲线可能表示电机在不同负载下的效率变化，而另一些曲线可能表示电机在不同速度下的转矩输出。

通过分析iq曲线，工程师可以了解电机在不同条件下的性能表现，从而优化控制策略、提高电机效率或调整电机参数以满足特定应用需求。

此外，iq曲线还可以用于评估电机的热性能、动态响应和稳定性等关键指标。

请注意，以上解释基于一般的电机控制理论，具体的iq曲线解释可能因电机类型、控制策略和应用场景的不同而有所差异。

同步电动机转矩－转差率曲线仿真1．原理说明同步电动机的起动常常采用异步启动法，它可以分为两个过程，即未加励磁前的异步运行过程和增加励磁以后的同步牵入过程。

同步电机的异步起动过程中的异步运行并非稳定的异步运行，而是伴随着电磁和机械的瞬态变化，但是由于转子具有较大的转动惯量，就其电磁过程而言，其机械加速度可以忽略不计，这样可以近似的当作一系列不同转差率的稳态异步运行状态来处理，所得的曲线就是所谓的似稳态曲线。

同步电机起动时由于转子绕组不对称，在起动的过程中将会产生单轴转矩，造成转矩－转差率曲线在s=0.5附近下凹，严重的甚至小于负载转矩，使电机无法正常起动。

研究和绘制同步电机起动时的转矩－转差率曲线对于电机设计具有重要的意义。

同步电机在稳态异步运行时，假设它的端电压为三相对称变化且频率为1f ，对应同步角速度为1ω，转子角速度为ω时，相应转差率为11()/s ωωω=-，它将在转子中感应出1sf 频率的电流。

由于转子绕组不对称，这个转子电流将产生分别以1()s ωω+和1()s ωω-速度相对定子旋转，它们分别在定子绕组中感应出1f 和1(12)s f -频率的对称电流。

另外，如果转子励磁绕组外加直流励磁电流时，它还要感应出1(1)s f -频率的对称电流。

这样，同步电机异步运行时，若存在直流励磁，则定子绕组中将产生1f ，1(1)s f -和1(12)s f -频率的谐波电流，转子励磁绕组中将有直流及1sf 频率的电流，阻尼绕组中有1sf 频率的电流。

这样定子绕组三相电流可以写成如下的表达式：12312312312312cos cos(12)cos(1)sin sin(12)sin(1)222cos()cos[(12)]cos[(1)]333222sin()sin[(12)][sin(1)]3332cos()cos[(123a b c i A t A s t A s t A t A s t A s t i A t A s t A s t A t A s t A s t i A t A πππππππ=+-+-+'''+-+-=-+--+--+'''-+--+--=++-312322)]cos[(1)]33222sin()sin[(12)][sin(1)]333s t A s t A t A s t A s t πππππ++-++'''++-++-+ 如令：*111111*222222*33333311(),()2211(),()2211(),()22I A jA I A jA I A jA I A jA I A jA I A jA ''=-=+''=-=+''=-=+ 为了计算上的方便，选用1、2、0坐标系统，将a 、b 、c 三相坐标转换为1、2、0坐标系统，可得,,a b c i i i 转换为1、2、0分量:(12)(1)1123**(12)*(1)212300jt j s t j s t jt j s t j s t i I e I e I e i Ie I e I e i -------=++=++= 同理，假定三相对称的端电压为：cos sin 22cos()sin()3322cos()sin()33a b c u B t B tu B t B t u B t B t ππππ'=+'=-+-'=+++并令：*1()21()2UB jB UB jB '=-'=+则1*200jt jt u Ueu U e u -=== 采用电动机惯例时，同步电机的磁链，电压，转矩方程分别为：1122211()()()21()()()2j j j j j f s D j j j j j f s D e G p u e x p e i e x p e i e G p u e x p e i e x p e i θθθθθθθθθθψψ-----⎫=++⎪⎪⎬⎪=++⎪⎭111222s s u p r i u p r i ψψ=+⎫⎬=+⎭12212()em T j i i ψψ=-其中()G p 为运算电导，1()[()()]2s d q x p x p x p =+为平均运算电抗，1()[()()]2D d q x p x p x p =-为半差运算电抗。

（2）机械特性曲线在一定的电源电压U 1和转子电阻R 2下，电动机的转矩T 与转差率n 之间的关系曲线T=f(s)或转速与转矩的关系曲线n=f(T)，称为电动机的机械特性曲线，如图所示。

在机械特性曲线上我们要讨论三个转矩：1）．额定转矩T N额定转矩T N 是异步电动机带额定负载时，转轴上的输出转矩。

29550N P T n =式中P 2是电动机轴上输出的机械功率，其单位是瓦特，n 的单位是转/分，T N 的单位是牛·米。

当忽略电动机本身机械摩擦转矩T 0时，阻转矩近似为负载转矩T L ，电动机作等速旋转时，电磁转矩T 必与阻转矩T L 相等，即T =T L 。

额定负载时，则有T N =T L 。

2）．最大转矩T mT m 又称为临界转矩，是电动机可能产生的最大电磁转矩。

它反映了电动机的过载能力。

最大转矩的转差率为S m ，此时的S m 叫做临界转差率，见图最大转矩Tm 与额定转矩T N 之比称为电动机的过载系数λ，即λ=Tm /T N一般三相异步的过载系数在1.8~2.2之间。

在选用电动机时，必须考虑可能出现的最大负载转矩，而后根据所选电动机的过载系数算出电动机的最大转矩，它必须大于最大负载转矩。

否则，就是重选电动机。

3）．起动转矩T st ，T st 为电动机起动初始瞬间的转矩，即n=0，s ＝１时的转矩。

为确保电动机能够带额定负载起动，必须满足：T st >T N ，一般的三相异步电动机有T st /T N =1~2.2。

27.5感应电动机的工作特性27.5.1转速特性：)(2P f n =空载时，转子转速接近于同步转速。

随着负载的增大，转速降低。

是一条稍微向下倾斜的曲线。

27.5.2定子电流特性：)(21P f I =定子电流含有两个分量，即L m I I I 11∙∙∙+=，空载时，负载分量接近于零；随负载的增大而转子电流增大，与之平衡的定子电流负载分量也随之增大。

27.5.3功率因数特性： )(cos 21P f =ϕ感应机的总阻抗是电感性的，其功率因数总是滞后的。

感应电动机的功率和电磁转矩异步电动机是一种机电能量改换元件，是通过电磁感应效果把电能传送到转子再转化为轴输出机械能。

本节从能量观念启航论说电动机的能量改换进程，剖析其功率和转矩的平衡联络。

一、功率改换进程和功率平衡方程式感应电机作业时，不行避免地存在着必定的损耗，本节偏重剖析各种损耗之间的联络。

由气隙旋转磁场通过电磁感应传递到转子的功率，称为电磁功率。

转子旋转的总机械功率转子轴端输出的机械功率P2感应电动机的功率平衡方程为：功率改换进程可喫苦率图（图1）标明。

图1感应电动机的功率图从电路的观念看这是在剖析感应电动机的特性中很首要的公式。

它阐明转差s 越大，电磁功率耗费在转子铜耗中的比重就越大，电动机的功率就越低，所以感应电动机通常都作业在s=0.02～0.06的计划内。

一同也阐明，只需知道了感应电动机的转子铜耗和转速，就可求出电磁功率和总机械功率。

二、转矩平衡方程式当电机安稳作业时，效果在电机上有三个转矩。

1）使电机旋转的转矩Tem。

2）由电机的机械损耗和附加损耗致使的空载制动转矩T0。

3)由电机所拖动的负载的反效果转矩T2。

显着Tem=T0+T2三、电磁转矩公式1.电磁转矩的物理表达式上式标明，电磁转矩的巨细与主磁通及转子电流的有功重量的乘积成正比，即电磁转矩是由气隙磁场与转子电流有功重量一同效果发作的。

电动机中电流.磁通与效果力这3个量的方向契合左手定则这一物理规矩，故称物理表达式。

首要用于定性剖析异步电动机电磁转矩巨细。

2.电磁转矩的参数表达式依据感应电动机的简化等效电路思考，可得由于式中标了解转矩T与转差率s的联络，所以也称为T—s曲线方程。

感应电动机的转矩—转差率曲线感应电动机的转矩—转差率曲线感应电动机的输出主要体现在转矩和转速上。

在电源为额定电压的情况下，电磁转矩与转差率的关系Ｔｅ＝ｆ（ｓ）就称为转矩—转差率特性，或Ｔｅ－ｓ曲线。

Ｔｅ－ｓ特性是感应电动机最主要的特性。

⼀、转矩—转差率特性从式（5-36）可知，电磁转矩从式（5-26）可知，转⼦电流为式中，，取转⼦电流的模代⼊电磁转矩Ｔｅ，可得（5-51）把不同的转差率ｓ代⼈上式，算出对应的电磁转矩Ｔｅ，便可得到转矩—转差率特性，如图5－25所⽰。

图中０<ｓ⼆、最⼤转矩和起动转矩最⼤转矩从图5—25可知，Ｔｅ－ｓ曲线有⼀个最⼤值Ｔｍａｘ．令，即可求出产⽣Ｔｍａｘ时的转差率ｓｍ为（5-52）ｓｍ称为临界转差率。

将ｓｍ代⼊式（5-51），可得（5-53）式中，正号对应于电动机状态，负号对应于发电机状态。

当Ｒ1? X1σ＋X′２σ，系数ｃ≈１时，ｓｍ和Ｔｍａｘ可近似的写成（5-54）从上式可见：(1)感应电机的最⼤转矩与电源电压的平⽅成正⽐，与定、转⼦漏抗之和近似成反⽐；(2)最⼤转矩的⼤⼩与转⼦电阻值⽆关，临界转差ｓｍ则与转于电阻Ｒ′2成正⽐：Ｒ′2增⼤时，ｓｍ增⼤，但Ｔmax保持不变，此时Ｔｅ－ｓ曲线的最⼤值将向左偏移,如图5-26所⽰。

电动机的最⼤转矩与额定转矩之⽐称为过载能⼒，⽤k T表⽰k T =Ｔmax/ＴN。

如果负载的制动转矩⼤于最⼤转矩,电动机就会停转。

为保证电动机不因短时过载⽽停转，通常k T＝1.6-2.5．起动转矩感应电动机接通电源开始起动时(s＝1)的电磁转矩称为起动转矩，⽤Ｔst表⽰。

将s＝1代⼊式(5-51)，可得（5-55）从上式和图5—26可见，增⼤转⼦电阻，ｓｍ就增⼤，起动转矩Ｔst将随之增⼤．直到达到最⼤转矩值为⽌。

对于绕线型电机，可以在转⼦中接⼈外加电阻来实现这⼀点。

三、转矩-转速特性(机械特性)把转矩-转差率曲线T。

= f(s)的纵、横坐标对调，井利⽤n=n s(1-s)把转差率转换为对应的转速n,就可以得到转矩—转速特性n= f(Ｔｅ)．如图5-27所⽰。

电机与拖动em MSP P T ==ΩΩ第三节感应电机的功率方程和转矩方程上节课22cos T m T c I φϕ=第四节感应电机的参数测试第五节感应电机的转矩-转差率曲线一、T-s 曲线•对电机来说，最重要的是T -n 特性；•一般用T -s 曲线来表示1、表达式-仍然用上节的表达式，结合等值电路推导-用T 型等值电路复杂，用近似Γ型等值电路emSp T =Ω''2212em rp m Is=第五节感应电机的转矩-转差率曲线一、T-s 曲线1、表达式'121d u I Z =1'2'22112()()u rr c x cx sσσ=+++2'112'2'21212(/)()S m u r T r cr s x cx s σσ=⋅⋅Ω+++2'112'2'21212/(/)()S m u r s r cr s x cx σσ=⋅Ω+++2'112'2'21212/(/)()S m u r sT r r s x x σσ=⋅Ω+++--常用的简化形式第五节感应电机的转矩-转差率曲线2、曲线-s =0时，T =0；物理意义：不切割磁力线-s ↑但很小，分子↓，分母↓↓，则T 近似正比于s ；物理意义：近似于弹簧-s ↑↑时，T =0，物理意义：定子磁场远远领先，一样不切割磁力线-曲线特点：存在最大值T m , 对应临界转差率s m2'112'2'21212/(/)()S m u r s T r r s x x σσ=⋅Ω+++第五节感应电机的转矩-转差率曲线T s 0 1 -1n电磁制动电动机发电机mT ms 0Sn stT -注意各区间对应的运行状态-注意n 轴和s 轴的对应点和方向关系第五节感应电机的转矩-转差率曲线二、机械特性-转速-转矩特性(n-T 特性)对应[0, n s ]的部分-根据稳定运行区域判据，一般的负载都是正向的特性，要求电机是负向特性-稳定运行区域只是在[0,s m ]-临界的意义TnmT Sn stT 负载特性工作点第五节感应电机的转矩-转差率曲线三、起动转矩特性-由图上可以得到起动转矩-结论：起动转矩不大！启动过程：“翻山越岭”2'112'2'21212()()st S m u r T r r x x σσ=⋅Ω+++1()|st s T T s ==s 01 mT ms 0Sn stT第五节感应电机的转矩-转差率曲线四、最大转矩特性1、数值'22'2112()m r S r x x σσ=±++2112'2111212(())m S m u T r r x x σσ=±Ω±+++'2m kr S x ≈±2112m S km uT x ≈±Ω第五节感应电机的转矩-转差率曲线四、最大转矩特性2、特点（1）显然U↓则Tm↓↓，感应电机的供电电压最敏感!（2）Tm 与r2无关但sm与r2有关，基本上是r2↑使sm↑, 则曲线顶点左移，Tst↑, 对起动有利（3）xk ↑，Tm↓，即漏抗越大，Tm越小（4）s正负不同时Tm大小稍有区别第五节感应电机的转矩-转差率曲线五、简化转矩公式•上面的公式太繁琐，用起来不方便•最有用的区域：对应机械特性那一段，对应（0，s m ]Ts 0mT m s 稳态运行区域第五节感应电机的转矩-转差率曲线五、简化转矩公式•方法：在最大转矩公式中引进s m ，•目的：在该区间用比较简化的形式代替原来的公式•引入：过载系数K T ：•为了保证电机过载时的正常运行，K T 一般取1.5~2.5m T NT K T =第五节感应电机的转矩-转差率曲线五、简化转矩公式•在T m , s m 已知的情况下，可以求出来对应任意s 的转矩值•求启动转矩（s =1）•求对应s =0.03时的转矩•问题：如何求T m , s m ？''221''22'22122()21[()()2]m m m m m r r r s T s s r r T s r r s s s s s +=≈+++2mm m T T s s s s =+N n 第五节感应电机的转矩-转差率曲线五、简化转矩公式•已知：P N ，n N ，K T •求：T N ，T m ，T st ……•步骤：•典型题（1）利用P N ，n N ，K T 求出来T N ，s N ，T m 260N N n πΩ=N N N P T =ΩS N N S n n s n −=m T NT k T =，s n第五节感应电机的转矩-转差率曲线五、简化转矩公式•典型题（2）利用额定点求出来s m ，max 21N N m Tm NT s s T K s s ==+2N m T m Ns s K s s +=2(1)m N T T s s K K +−=--关于s m 的一元二次方程第五节感应电机的转矩-转差率曲线五、简化转矩公式•典型题（3）求其他转矩值m 2()m m T T f s s s s s ==+-代入s 数值，可以求出来对应任意s 的转矩值第一部分电机原理第五章感应电机思考问题：1、理解感应电机T-s曲线的特征。