庐江县市调报告2012年11月

全年受理专利申请15142件，其中发明专利4748件，增长31.2%；授权专利9639件，其中发明专利1242件，增长63.4%。

签订各类技术合同5160项，成交金额42.3亿元，增长26.9%。

全市有6项成果获国家科技奖，其中国家自然科学二等奖3项、科技进步二等奖3项。

十、文化、卫生和体育年末全市共有文化馆12个，公共图书馆9个，博物馆18个，各级各类档案馆12个。

全国重点文物保护单位 3处，省级重点文物保护单位39处，市（县）级重点文物保护单位245处。

国家级非物质文化遗产项目 4 项，省级非物质文化遗产项目11项，市级非物质文化遗产项目59项。

图书馆总藏量697.05万册（件），其中图书325.10万册，比上年分别增长42.0%和4.6%。

各级国家档案馆馆藏档案资料214.42万卷，增长67.9%。

电影院26家，全年票房收入1.85亿元，增长41.2%。

各类动漫企业85家，具有原创能力和代表作品的企业35家。

年末广播综合人口覆盖率和电视综合人口覆盖率均达100%。

年末全市共有卫生机构（含村卫生室）2100个，其中医院、卫生院260个，妇幼保健院（所、站）12个，卫生防疫和防治机构11个，社区卫生服务机构216个。

卫生机构床位数3.72万张，其中医院、卫生院床位3.47万张。

专业卫生技术人员4.04万人，其中执业（助理）医师1.53万人，注册护士1.82万人。

每千人拥有卫生技术人员5.33人，拥有医院、卫生院床位4.58张。

婴儿死亡率5.93‰，产妇住院分娩率99.98%。

城市社区卫生机构覆盖率达95%，城乡居民新农合参合率达100.37%。

全年成功组织2项大型赛事和18项市级体育赛事。

我市体育健儿参加各种赛事获得13枚金牌、5枚银牌和7枚铜牌。

全市完成260个农民体育健身工程和70个全民健身苑工程建设。

十一、人口、人民生活和社会保障年末全市常住人口757.2万人，比上年增加5.1万人。

城镇化率为66.4%，比上年提高1.8个百分点。

目录2012年中国各省GDP排名 (3)1、2012年广东各地区GDP排名 (5)2、2012年江苏省各地区GDP (6)3、2012年山东省各地区GDP (7)4、2012年浙江省各地区GDP (8)5、2012年河南省各地区GDP (9)6、2012年河北省各地区GDP (10)7、2012年辽宁省各地区GDP (11)8、2012年上海各地区GDP (12)9、2012年四川省各地区GDP (13)10、2012年湖北省各地区GDP (14)11、2012年湖南省各地区GDP (17)12、2012年福建省各地区GDP (18)2012年福建各地市GDP (18)13、2012年北京各地区GDP (19)14、2012年安徽省各地区GDP (20)15、2012年内蒙古各地区GDP排名 (21)16、2012年黑龙江各地区GDP (22)17、2012年陕西各地区GDP (24)18、2012年广西省各地区GDP (25)19、2012年天津各地区GDP (26)20、2012年江西各地区GDP (27)21、2012年吉林各地区GDP (28)22、2012年山西各地区GDP (30)23、2012年重庆各地区GDP (32)24、2012年云南各地区GDP (34)25、2012年新疆各地区GDP (35)26、2012年贵州省各地区GDP (36)27、2012年甘肃省各地区GDP (37)28、2012年海南省各地区GDP (38)29、2012年宁夏省各地区GDP (39)30、2012年青海省各地区GDP (40)31、2012年西藏各地区GDP (41)2012年中国各省GDP排名排名省份GDP（单位：亿元人民币）1广东53477.4082江苏48604.1523山东45429.9854浙江32000.4455河南27598.9756河北24674.2627辽宁225308上海19731.649四川21139.26710湖北19650.75211湖南19520.40212福建25273.92313北京16382.42414安徽1530815内蒙11517.8116黑龙江14318.73617陕西12266.75618广西11284.619天津11180.875 20江西11153.432 21吉林10475.2 22山西11235.1 23重庆10018.07 24云南8756.244 25新疆6519.068 26贵州5644.14 27甘肃5090.82 28海南2526.17 29宁夏2085.430青海1636.59 31西藏6051、2012年广东各地区GDP排名1. 广州 12560.7亿12.7%2. 深圳 11358.3亿10.5%3. 佛山6788.2亿13.9%4. 东莞4698.9亿9.2%5. 中山2225.3亿14.3%6. 惠州2172.8亿15.3%7. 江门1879.4亿11.9%8. 湛江 1789.0亿12.2%9. 茂名1701.4亿10.1%10.汕头1433.8亿12.5%11.珠海1418.5亿13.2%12.肇庆1291.2亿17.1%13.清远1268.7亿17.2%14.揭阳1237.7亿16.7%15.阳江797.1亿16.1%16.韶关779.7亿13.0%17.梅州724.8亿14.8%18.潮州656.1亿14.2%19.河源575.6亿15.4%20.汕尾553.7亿14.7%21.云浮481.3亿16.7%2、2012年江苏省各地区GDP城市 GDP 增速3、2012年山东省各地区GDP2012年，青岛实现地区生产总值7302.11亿元,同比增长10.6% 2012年，烟台实现地区生产总值5280亿，比上年增长10.2%2012年，济南实现地区生产总值4812.68亿元，比上年增长9.5% 2012年，潍坊实现地区国内生产总值4012亿元，同比增长10.6% 2012年，淄博实现地区生产总值3557.2亿元,比上年增长10.5% 2012年，济宁实现地区生产总值达到3210亿元、增长11%；2012年，临沂市实现地区生产总值3012.8亿元，增长11.8%；2012年，东营市实现地区生产总值3000.66亿元，增长12.1% 2012年，泰安市实现地区生产总值2604亿元,增长10.5%左右2012年，威海市实现生产总值2330亿元，增长9.5%左右2012年，德州实现地区生产总值2230亿元，增长12%。

最高人民检察院发布6起侵害未成年人案件强制报告追责典型案例（2022年5月27日）许某某等人强奸案一住宿经营者怠于履行强制报告义务受到处罚一、基本案情2021年6月7日晚，许某某、陈某、王某、王某某（未成年人）、唐某某（未成年人）等5人在广西桂林某烧烤店吃饭。

其间，王某看到刘某带李某某（女，未成年人）回家，提议将欠烧烤店钱的刘某打一顿，许某某提出想与李某某发生性关系。

随后，几人来到刘某租住的居民楼，对刘某和李某某进行殴打，并强行将李某某带到宾馆。

许某某、陈某、王某某三人在宾馆房间强行与李某某发生性关系。

6月10日，李某某报警。

10月15日，桂林市七星区人民检察院以涉嫌强奸罪对许某某等5人提起公诉。

桂林市七星区人民法院判处许某某、陈某有期徒刑十年零三个月，王某某有期徒刑七年，王某有期徒刑五年，唐某某有期徒刑二年六个月。

经查，案发当晚，本案6名当事人入住桂林某宾馆，其中包括 3 名未成年人。

宾馆在接待上述未成年人与成年人共同入住时，既未严格落实登记制度，逐人核实身份信息，也未询问入住未成年人相关情况。

通过查看宾馆监控视频，办案人员发现被害人李某某与许某某等人共同进入宾馆后，始终被唐某某拉着手，被害人神情疲惫，脚步迟缓，表现明显异常，多次在距离宾馆前台2米远的沙发处停留。

宾馆工作人员发现异常情况后，未询问情况或与监护人联系，也未按照强制报告要求向公安机关报案，怠于履行强制报告义务。

二、处理情况该案发生前夕，桂林市七星区人民检察院和市公安局七星分局联合召开了旅馆业落实强制报告制度推进会，向辖区旅馆、宾馆、酒店等住宿经营者通报了未成年人保护法关于强制报告的有关规定。

涉案宾馆明知法律规定，发现问题仍置之不理。

因宾馆未尽到安全保护责任，李某某被多人毫无障碍地带入宾馆房间并遭到多人性侵害。

2021 年8月11日，桂林市公安局七星分局依据《中华人民共和国未成年人保护法》第一百二十二条规定，对涉案宾馆作出罚款二万元，责令停业整顿一个月的处罚决定。

安徽省滁州市明光市2012年政府工作报告——2012年1月16日在明光市第十五届人民代表大会第一次会议上市人民政府市长杨甫祥各位代表：现在，我代表市人民政府，向大会作政府工作报告，请予审议，并请市政协委员和其他列席人员提出意见。

一、过去五年工作回顾市第十四届人民代表大会第一次会议以来的五年，是明光发展史上极不平凡的五年，是明光经济社会负重爬坡、加速发展的五年。

五年来，在市委的坚强领导下，在市人大、市政协的监督支持下，市政府团结带领全市人民，深入贯彻落实科学发展观，按照“四个二” 1发展思路，科学应对国际金融危机冲击，成功战胜各种自然灾害挑战，克难攻坚，开拓进取，全面完成了市十四届人大一次会议确定的各项目标任务，明光开始迈入了加快发展的新阶段。

五年来，始终以科学发展为主题，综合实力跃上新台阶。

坚持发展第一要务，认真贯彻落实中央、省和滁州市的决策部署，危机中抓机遇，困境中谋发展，奋力做好保增长、调结构、促改革、惠民生的各项工作。

五年累计完成固定资产投资175亿元，有力拉动了经济社会发展。

预计2011年，全市实现地区生产总值79亿元，比2006年的37.3亿元增加41.7亿元，五年年均增长11.8%；财政收入7.16亿元，是2006年的3.6倍，年均增长28.9%；固定资产投资60亿元，是2006年的5.4倍，年均增长40.1%；在岗职工年平均工资25970元，农民人均纯收入6565元，均是2006年的2.1倍。

工业经济取得新突破。

围绕我市业已形成的食品饮料、日用化工、机械电子、新型材料、矿产加工、服装玩具等六个主导产业，在提升产业层次、壮大产业规模上下功夫，推进大企业上台阶、中企业上水平、小企业上规模。

三次产业结构由37.5：24.9：37.6调整为31：33：36，工业主导型经济发展格局初见雏形。

2011年实现工业增加值20亿元，比2006年的8亿元增加12亿元。

全市规模以上工业企业发展到68家，其中亿元以上企业20家。

————合肥合肥是安徽省省会，全省政治、经济、文化、科教、商贸、交通和信息中心。

合肥享有“三国故地”、“包拯家乡”、“淮军摇篮”、“科教基地”、“滨湖新城”之美誉,因东淝河与南淝河由此发源，故曰“合肥”；因明清时为庐州府治所在，故别称“庐州”。

合肥地处长江淮河之间，巢湖之滨，泛长三角区域西端；通江达海，承东启西，贯通南北，连接中原的重要区位优势。

市域总面积7029.48平方公里，户籍总人口486.74万人，城镇化率62.4％。

现辖肥东、肥西、长丰3个县，瑶海、庐阳、蜀山、包河4个区，赋予合肥国家级高新技术产业开发区、合肥国家级经济技术开发区、合肥新站综合试验区市级管理权限。

目录合肥的地形地貌及地理位置 (3)合肥的名称由来及历史 (4)合肥的城市职能及城市性质 (5)合肥的行政区划及区划概况 (7)合肥的交通 (9)合肥的经济概况 (10)合肥的地形地貌及地理位置合肥的地理位置合肥市位于安徽省中部，北纬31度52分、东经117度17分。

北与淮南市接壤，南与芜湖市相连，东与滁州市、马鞍山市毗邻，西与六安市、安庆市交界合肥的地形地貌[1]合肥地处江淮腹地丘陵地区，由西向东的江淮分水岭贯穿市境，形成低缓的鱼背形地势。

全市地形分为丘陵、岗地、平原圩区三大类。

西南园洞山一带海拔相对较高，其余大部分属低短龚岗地带合肥的名称由来及历史设立时间与背景秦汉之交，合肥正式建立“合肥县”，属九江郡。

东汉刘秀升合肥为侯国，三国时为扬州治所，三国时魏将张辽大败孙权十万大军的逍遥津战役，即发生在这里。

明清时为庐州府治，故又别称为“庐州”。

自东汉末以来，合肥数为州郡治所，一直是江淮地区重要的行政中心和军事重镇。

清咸丰年间，合肥曾为安徽省省会，1945年国民政府安徽省省会迁入合肥，1949年1月21日合肥解放，同年2月合肥建市。

1952年，新中国安徽省人民政府正式在合肥市成立。

合肥城址屡有变迁。

《太平寰宇记》记载：汉代合肥县城“在今县（城）北”，位于今四里河附近，今长丰路以西“古城郢”，面积很小。

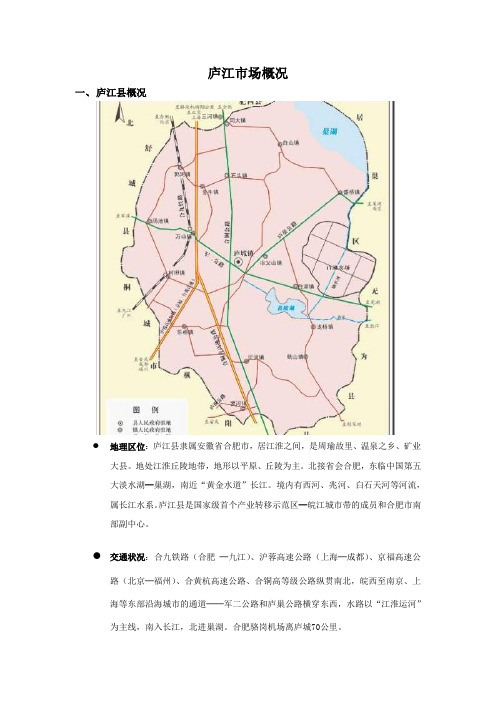
庐江市场概况一、庐江县概况●地理区位：庐江县隶属安徽省合肥市，居江淮之间，是周瑜故里、温泉之乡、矿业大县。

地处江淮丘陵地带，地形以平原、丘陵为主。

北接省会合肥，东临中国第五大淡水湖━巢湖，南近“黄金水道”长江。

境内有西河、兆河、白石天河等河流，属长江水系。

庐江县是国家级首个产业转移示范区━皖江城市带的成员和合肥市南部副中心。

●交通状况：合九铁路（合肥─九江）、沪蓉高速公路（上海─成都）、京福高速公路（北京─福州）、合黄杭高速公路、合铜高等级公路纵贯南北，皖西至南京、上海等东部沿海城市的通道──军二公路和庐巢公路横穿东西，水路以“江淮运河”为主线，南入长江，北进巢湖。

合肥骆岗机场离庐城70公里。

●地域概况：全县面积2352平方公里,人口120万。

其中常驻人口为97.4万。

2012年庐江城区人口27万，建成区面积为26平方公里。

下辖庐城镇（县城）、冶父山镇等共17个镇，。

●经济概况：2010年地区生产总值突破100亿元，达103.2亿元，增长11%。

财政收入突破10亿元，增加2.34亿元，增长30.4%，增幅居全市第一；超千万元镇达13个。

规模以上工业增加值21.3亿元，增长24%。

固定资产投资92亿元，增长37.3%；社会消费品零售总额42.1亿元，增长19.2%。

外贸进出口总额4800万美元，增长28.4%；外贸自营权企业新增21家。

2011年完成地区生产总值（GDP)138.3亿元，人均地区生产总值1.16万元。

财政收入15亿元，固定资产投资90亿元，规模工业增加值29亿元，在岗职工平均工资3.15万元，农民人均纯收入6952元，城乡居民储蓄存款余额122亿元，社会消费品零售总额49.2亿元。

2012年全县实现生产总值156.87亿元，按可比价格计算，增长13.3%。

2012年，实现规模以上工业增加值、固定资产投资、社会消费品零售总额和财政收入达34.02、144.49、57.95和20.25亿元，分别增长26%、68.2%、17.4%和35%，分别高于全市8.6、44.5、0.7和23.7个百分点，分别位居全市（四县一市）第3、1、4和2位。

c）？1、从严格意义上看经济法主体，下列不属于经济法的主体（自然人C.个体户人民法院 D.A.公司 B. 全国人名代表大会及其常务委员会2、狭义上的法律是指由（）制定、颁布的规范性文件？5000）？3、抽奖式的有奖销售，最高的金额不得超过（A）？4、可以作为公司资本作为出资（B.必须用资金A.可以用劳务D.必须用资金或实物必须用实物C.人民币5、新修订的《公司法》规定，有限责任公司注册资本的最低限额为人民币（三万）？股票发行市场上公开发行股票的股份有限公（、6、股票的发行者是6司）？一年内7、具有撤销权的当事人自知道或者应当知道撤销事由之日起（）行使撤销权？双倍、合同生效后，收受定金的一方不履行合同的，应当（）？8、甲将其电脑借给乙使用，乙却将该电脑卖给丙。

依据我国《合同法》的规定，下列关于9在获得追认或者取得处分权之前，（乙丙之间买卖电脑的合同效力的表述中）合同效力尚未确定，称为效力待定。

是正确的？D？)10、根据担保法的规定，下列财产中，可以用作抵押的是( 所有权有争议的财产 B. A. 土地所有权抵押人自有的厂房 D. C. 依法被扣押的财产11、根据我国消费者权益保护法的规定，消费者是指（消费者是指为生活消费需要而购买、使用商品或者接受服务的自然人。

）？12、14岁的中学生刘某在超市买了一双价值50元人民币的普通球鞋，这一买卖行为（有效）？13、张某是某企业的销售人员，随身携带盖有该企业公章的空白合同书，便于对外签约。

后张某因收取回扣被企业除名，但空白合同书未被该企业收回。

张某以此合同书与他人签订购销协议，该购销协议的性质应认定（成立并生效）？14、根据我国《消费者权益保护法》的规定，消费者协会是依法成立的对商品和服务进行社会监督和保护消费者合法权益的（ D ）A．国家机关B．行业管理部门C．行业自律组织D．社会团体15、劳动法调整的各种社会关系中，居于核心地位的是（D）？涉及工会组织的社会关系B. 劳动行政关系A.劳动争议处理关系 D. 劳动关系 C.消使用直接用于农业生产的生产资料，其合法权益受到侵害的，可参照执行16、农民购买、费者权益保护法应的，)万17、证券法规定向不特定对象公开发行的证券票面总值超过人民币( 5000当委托承销机构。

【认识巢湖】县区篇居巢区居巢之称始于秦朝，唐朝设立巢县，1984年设立县级巢湖市，1999年底撤市改称居巢区，为巢湖市委、市政府所在地。

全区总面积2031平方公里，总人口86万，下辖12个乡镇、5个街道办事处，其中副县级中心镇4个，是全市政治、经济和文化中心。

居巢四季分明，气候宜人。

年平均气温在15.7℃～16.1℃，全年无霜期在232天～247天，年降水量在1000毫米～1158毫米之间。

居巢人杰地灵，物产丰富，是安徽省重点旅游开放、开发区和著名的风景疗养区。

古是楚汉相争时期政治家范增的出生地，近为冯玉祥、张治中、李克农、温宗仁“四将军”的故里。

800里巢湖烟波浩淼，景色秀丽；姥山岛九峰起伏，宛如蓬境；银屏仙人洞幽深宜人，悬崖上的千年牡丹独特奇异，每年谷雨时节含芳怒放；半汤温泉是安徽休闲疗养的主要区域，富含30多种活性元素；北郊的王乔洞，是江淮大地上唯一的一座摩崖石窟；紫薇洞长达千米，被誉为江淮第一自然溶洞。

全区盛产粮、棉、麻、蔬菜及畜禽、水果等200多种农副产品，素有“鱼米之乡”的美誉。

境内矿藏丰富，工业品有水泥、锚链、渔网、花炮和纺织品等200多个品种。

居巢区历史悠久，有文字记载的有三千多年。

商是时地属南疆，故称南巢。

周时为巢(伯)国地，春秋时为楚属国。

秦统一后置郡县，今巢湖以南为居巢县。

唐武德七年(公元624年)，合开城、扶阳两县为巢县(巢县一名此始)，隶属庐州。

北宋太平兴国三年（公元978年）巢县属无为军。

南宋景定三年(公元1262年)升巢县为镇巢军，至元二十八年(公元1291年)置巢州为县，巢县县名至改置巢湖市前一直未变。

民国元年属安徽省。

民国28年由属第三专区改第五专区。

1949年4月属巢湖专区，1952年属芜湖专区，1958年属合肥市。

1961年4月复属芜湖专区，1965年复设巢湖专区，巢县隶属之。

1971年8月巢湖专区改称巢湖地区，巢县隶属不变。

1984年1月4日撤县改市成立巢湖市，属巢湖地区。

庐江县第二中学2018-2019学年高三上学期11月月考数学试卷含答案一、选择题1． 已知函数[)[)1(1)sin 2,2,212()(1)sin 22,21,222nn x n x n n f x x n x n n ππ+⎧-+∈+⎪⎪=⎨⎪-++∈++⎪⎩（n N ∈），若数列{}m a 满足*()()m a f m m N =∈，数列{}m a 的前m 项和为m S ，则10596S S -=（ ） A.909 B.910 C.911 D.912【命题意图】本题考查数列求和等基础知识，意在考查分类讨论的数学思想与运算求解能力. 2． 数列﹣1，4，﹣7，10，…，（﹣1）n （3n ﹣2）的前n 项和为S n ，则S 11+S 20=（ ）A ．﹣16B ．14C ．28D ．303． 若变量x ，y满足：，且满足（t+1）x+（t+2）y+t=0，则参数t 的取值范围为（ ）A ．﹣2＜t＜﹣ B ．﹣2＜t ≤﹣ C ．﹣2≤t ≤﹣ D ．﹣2≤t＜﹣4． 下列图象中，不能作为函数y=f （x ）的图象的是（ ）A． B．C．D．5． 设定义域为（0，+∞）的单调函数f （x ），对任意的x ∈（0，+∞），都有f[f （x ）﹣lnx]=e+1，若x 0是方程f （x ）﹣f ′（x ）=e 的一个解，则x 0可能存在的区间是（ ） A ．（0，1） B ．（e ﹣1，1） C ．（0，e ﹣1）D ．（1，e ）6． 过点),2(a M -，)4,(a N 的直线的斜率为21-，则=||MN （ ） A ．10 B ．180 C ．36 D ．56班级_______________ 座号______ 姓名_______________ 分数__________________________________________________________________________________________________________________7．以的焦点为顶点，顶点为焦点的椭圆方程为（）A．B．C．D．8．把函数y=cos（2x+φ）（|φ|＜）的图象向左平移个单位，得到函数y=f（x）的图象关于直线x=对称，则φ的值为（）A．﹣B．﹣C．D．9．沿一个正方体三个面的对角线截得几何体如图所示，则该几何体的侧视图为（）A．B．C．D．10．对“a，b，c是不全相等的正数”，给出两个判断：①（a﹣b）2+（b﹣c）2+（c﹣a）2≠0；②a≠b，b≠c，c≠a不能同时成立，下列说法正确的是（）A．①对②错B．①错②对C．①对②对D．①错②错11．已知数列，则5是这个数列的（）A．第12项B．第13项C．第14项D．第25项12．在△ABC中，，则这个三角形一定是（）A．等腰三角形B．直角三角形C．等腰直角三角 D．等腰或直角三角形二、填空题13．已知等比数列{a n}是递增数列，S n是{a n}的前n项和．若a1，a3是方程x2﹣5x+4=0的两个根，则S6=．，两类产品，甲种设备每天能生产A类产品5件和B类产品10件，14．某公司租赁甲、乙两种设备生产A B乙种设备每天能生产A类产品6件和B类产品20件.已知设备甲每天的租赁费为200元，设备乙每天的租赁费用为300元，现该公司至少要生产A类产品50件，B类产品140件，所需租赁费最少为__________元.15．设函数f（x）=的最大值为M，最小值为m，则M+m=．16．已知数列的前项和是, 则数列的通项__________17．如图，长方体ABCD﹣A1B1C1D1中，AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，则异面直线A1E与GF所成的角的余弦值是．18．等比数列{a n }的前n 项和为S n ，已知S 3=a 1+3a 2，则公比q= ．三、解答题19．（本小题满分10分）选修4-4：坐标系与参数方程在直角坐标系xOy 中，过点(1,2)P -的直线l 的倾斜角为45．以坐标原点为极点，x 轴正半轴为极坐标建立极坐标系，曲线C 的极坐标方程为2sin 2cos ρθθ=,直线l 和曲线C 的交点为,A B ． （1（220．（本小题满分12分）若二次函数()()20f x ax bx c a =++≠满足()()+12f x f x x -=,且()01f =.（1）求()f x 的解析式； （2）若在区间[]1,1-上，不等式()2f x x m >+恒成立，求实数m 的取值范围．21．（本小题满分12分）某单位共有10名员工，他们某年的收入如下表：员工编号 1 2 3 4 5 6 7 8 9 10 年薪（万元）33．5455．56．577．5850（1）求该单位员工当年年薪的平均值和中位数；（2）从该单位中任取2人，此2人中年薪收入高于5万的人数记为ξ，求ξ的分布列和期望；（3）已知员工年薪收入与工作年限成正相关关系，某员工工作第一年至第四年的年薪分别为3万元、5.4万元、6.5万元、2.7万元，预测该员工第五年的年薪为多少？附：线性回归方程a x b yˆˆˆ+=中系数计算公式分别为： 121()()()niii nii x x y y b x x ==--=-∑∑，x b y aˆˆ-=，其中x 、为样本均值．22．已知f （x ）=lg （x+1）（1）若0＜f （1﹣2x ）﹣f （x ）＜1，求x 的取值范围；（2）若g （x ）是以2为周期的偶函数，且当0≤x ≤1时，g （x ）=f （x ），求函数y=g （x ）（x ∈[1，2]）的反函数．23．（本题满分15分）正项数列}{n a 满足121223+++=+n n n n a a a a ，11=a ．（1）证明：对任意的*N n ∈，12+≤n n a a ；（2）记数列}{n a 的前n 项和为n S ，证明：对任意的*N n ∈，32121<≤--n n S ．【命题意图】本题考查数列的递推公式与单调性，不等式性质等基础知识，意在考查推理论证能力，分析和解决问题的能力.24．在△ABC 中，cos2A ﹣3cos （B+C ）﹣1=0． （1）求角A 的大小；（2）若△ABC 的外接圆半径为1，试求该三角形面积的最大值．庐江县第二中学2018-2019学年高三上学期11月月考数学试卷含答案（参考答案）一、选择题1．【答案】A.【解析】2．【答案】B【解析】解：∵a n=（﹣1）n（3n﹣2），∴S11=（）+（a2+a4+a6+a8+a10）=﹣（1+7+13+19+25+31）+（4+10+16+22+28）=﹣16，S20=（a1+a3+…+a19）+（a2+a4+…+a20）=﹣（1+7+...+55）+（4+10+ (58)=﹣+=30，∴S11+S20=﹣16+30=14．故选：B．【点评】本题考查数列求和，是中档题，解题时要认真审题，注意分组求和法和等差数列的性质的合理运用．3．【答案】C【解析】解：作出不等式组对应的平面区域如图：（阴影部分）．由（t+1）x+（t+2）y+t=0得t（x+y+1）+x+2y=0，由，得，即（t+1）x+（t+2）y+t=0过定点M（﹣2，1），则由图象知A，B两点在直线两侧和在直线上即可，即[2（t+2）+t][﹣2（t+1）+3（t+2）+t]≤0，即（3t+4）（2t+4）≤0，解得﹣2≤t≤﹣，即实数t的取值范围为是[﹣2，﹣]，故选：C．【点评】本题主要考查线性规划的应用，利用数形结合是解决本题的关键．综合性较强，属于中档题．4．【答案】B【解析】解：根据函数的定义可知，对应定义域内的任意变量x只能有唯一的y与x对应，选项B中，当x ＞0时，有两个不同的y和x对应，所以不满足y值的唯一性．所以B不能作为函数图象．故选B．【点评】本题主要考查函数图象的识别，利用函数的定义是解决本题的关键，注意函数的三个条件：非空数集，定义域内x的任意性，x对应y值的唯一性．5．【答案】D【解析】解：由题意知：f（x）﹣lnx为常数，令f（x）﹣lnx=k（常数），则f（x）=lnx+k．由f[f（x）﹣lnx]=e+1，得f（k）=e+1，又f（k）=lnk+k=e+1，所以f（x）=lnx+e，f′（x）=，x＞0．∴f（x）﹣f′（x）=lnx﹣+e，令g（x）=lnx﹣+﹣e=lnx﹣，x∈（0，+∞）可判断：g（x）=lnx﹣，x∈（0，+∞）上单调递增，g（1）=﹣1，g（e）=1﹣＞0，∴x0∈（1，e），g（x0）=0，∴x0是方程f（x）﹣f′（x）=e的一个解，则x0可能存在的区间是（1，e）故选：D．【点评】本题考查了函数的单调性，零点的判断，构造思想，属于中档题．6．【答案】D【解析】考点：1.斜率；2.两点间距离.7．【答案】D【解析】解：双曲线的顶点为（0，﹣2）和（0，2），焦点为（0，﹣4）和（0，4）．∴椭圆的焦点坐标是为（0，﹣2）和（0，2），顶点为（0，﹣4）和（0，4）．∴椭圆方程为．故选D．【点评】本题考查双曲线和椭圆的性质和应用，解题时要注意区分双曲线和椭圆的基本性质．8．【答案】B【解析】解：把函数y=cos（2x+φ）（|φ|＜）的图象向左平移个单位，得到函数y=f（x）=cos[2（x+）+φ]=cos（2x+φ+）的图象关于直线x=对称，则2×+φ+=kπ，求得φ=kπ﹣，k∈Z，故φ=﹣，故选：B．9．【答案】A【解析】解：由已知中几何体的直观图，我们可得侧视图首先应该是一个正方形，故D不正确；中间的棱在侧视图中表现为一条对角线，故C不正确；而对角线的方向应该从左上到右下，故B不正确故A选项正确．故选：A．【点评】本题考查的知识点是简单空间图象的三视图，其中熟练掌握简单几何体的三视图的形状是解答此类问题的关键．10．【答案】A【解析】解：由：“a，b，c是不全相等的正数”得：①（a﹣b）2+（b﹣c）2+（c﹣a）2中至少有一个不为0，其它两个式子大于0，故①正确；但是：若a=1，b=2，c=3，则②中a≠b，b≠c，c≠a能同时成立，故②错．故选A．【点评】本小题主要考查不等关系与不等式等基础知识，考查运算求解能力，考查逻辑思维能力．属于基础题．11．【答案】B【解析】由题知，通项公式为，令得，故选B答案：B12．【答案】A【解析】解：∵，又∵cosC=，∴=，整理可得：b2=c2，∴解得：b=c．即三角形一定为等腰三角形．故选：A．二、填空题13．【答案】63【解析】解：解方程x2﹣5x+4=0，得x1=1，x2=4．因为数列{a n}是递增数列，且a1，a3是方程x2﹣5x+4=0的两个根，所以a1=1，a3=4．设等比数列{a n}的公比为q，则，所以q=2．则．故答案为63．【点评】本题考查了等比数列的通项公式，考查了等比数列的前n 项和，是基础的计算题．14．【答案】2300 【解析】111]试题分析：根据题意设租赁甲设备，乙设备，则⎪⎪⎩⎪⎪⎨⎧≥+≥+≥≥14020y 10x 506y 5x 0y 0x ，求目标函数300y 200x Z +=的最小值.作出可行域如图所示，从图中可以看出，直线在可行域上移动时，当直线的截距最小时，取最小值2300.1111]考点：简单线性规划.【方法点晴】本题是一道关于求实际问题中的最值的题目，可以采用线性规划的知识进行求解；细查题意，设甲种设备需要生产天，乙种设备需要生产y 天，该公司所需租赁费为Z 元，则y x Z 300200+=，接下来列出满足条件的约束条件，结合目标函数，然后利用线性规划的应用，求出最优解，即可得出租赁费的最小值. 15．【答案】 2 ．【解析】解：函数可化为f （x ）==，令，则为奇函数，∴的最大值与最小值的和为0．∴函数f（x）=的最大值与最小值的和为1+1+0=2．即M+m=2．故答案为：2．16．【答案】【解析】当时，当时，，两式相减得：令得，所以答案：17．【答案】0【解析】【分析】以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，利用向量法能求出异面直线A1E与GF所成的角的余弦值．【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，∵AA1=AB=2，AD=1，点E、F、G分别是DD1、AB、CC1的中点，∴A1（1，0，2），E（0，0，1），G（0，2，1），F（1，1，0），=（﹣1，0，﹣1），=（1，﹣1，﹣1），=﹣1+0+1=0，∴A1E⊥GF，∴异面直线A1E与GF所成的角的余弦值为0．故答案为：0．18．【答案】2．【解析】解：设等比数列的公比为q ，由S 3=a 1+3a 2，当q=1时，上式显然不成立；当q ≠1时，得，即q 2﹣3q+2=0，解得：q=2． 故答案为：2．【点评】本题考查了等比数列的前n 项和，考查了等比数列的通项公式，是基础的计算题．三、解答题19．【答案】【解析】（1）∵直线l 过点(1,2)P -，且倾斜角为45．∴直线l 的参数方程为1cos 452sin 45x t y t ⎧=+⎪⎨=-+⎪⎩（t 为参数）， 即直线l的参数方程为122x y ⎧=+⎪⎪⎨⎪=-⎪⎩（t 为参数）．（2）∵2sin 2cos ρθθ=，∴2(sin )2cos ρθρθ=，∵cos x ρθ=，sin y ρθ=，∴曲线C 的直角坐标方程为22y x =，∵1222x t y ⎧=+⎪⎪⎨⎪=-+⎪⎩，∴2(2)2(1)22-+=+，∴240t -+=，∴124t t =，20．【答案】（1）()2=+1f x x x -；（2）1m <-． 【解析】试题分析：（1）根据二次函数()()20f x ax bx c a =++≠满足()()+12f x f x x -=，利用多项式相等，即可求解,a b 的值，得到函数的解析式；（2）由[]()1,1,x f x m ∈->恒成立，转化为231m x x <-+，设()2g 31x x x =-+，只需()min m g x <，即可而求解实数m 的取值范围． 试题解析：（1） ()()20f x ax bx c a =++≠ 满足()01,1f c == ()()()()2212,112f x f x x a x b x ax bx x +-=+++--=，解得1,1a b ==-,故()2=+1f x x x -.考点：函数的解析式；函数的恒成立问题. 【方法点晴】本题主要考查了函数解析式的求解、函数的恒成立问题，其中解答中涉及到一元二次函数的性质、多项式相等问题、以及不等式的恒成立问题等知识点的综合考查，着重考查了学生分析问题和解答问题的能力，推理与运算能力，以及转化与化归思想，试题有一定的难度，属于中档试题，其中正确把不等式的恒成立问题转化为函数的最值问题是解答的关键.21．【答案】【解析】（1）平均值为10万元，中位数为6万元．（2）年薪高于5万的有6人，低于或等于5万的有4人；ξ取值为0，1，2．152)0(21024===C C P ξ，158)1(2101614===C C C P ξ，31)2(21026===C C P ξ， ∴ξ的分布列为∴()012151535E ξ=⨯+⨯+⨯=． （3）设)4,3,2,1(,=i y x i i 分别表示工作年限及相应年薪，则5,5.2==y x ，21() 2.250.250.25 2.255n ii x x =-=+++=∑， 41()() 1.5(2)(0.5)(0.8)0.50.6 1.5 2.27ii i x x y y =--=-⨯-+-⨯-+⨯+⨯=∑，121()()7 1.45()n i ii n ii x x y y b x x ==--===-∑∑，ˆˆ5 1.4 2.5 1.5a y b x =-=-⨯=， 由线性回归方程为 1.4 1.5y x =+．可预测该员工年后的年薪收入为8.5万元．22．【答案】【解析】解：（1）f （1﹣2x ）﹣f （x ）=lg （1﹣2x+1）﹣lg （x+1）=lg （2﹣2x ）﹣lg （x+1），要使函数有意义，则由解得：﹣1＜x ＜1．由0＜lg （2﹣2x ）﹣lg （x+1）=lg＜1得：1＜＜10， ∵x+1＞0，∴x+1＜2﹣2x＜10x+10，∴．由，得：．（2）当x∈[1，2]时，2﹣x∈[0，1]，∴y=g（x）=g（x﹣2）=g（2﹣x）=f（2﹣x）=lg（3﹣x），由单调性可知y∈[0，lg2]，又∵x=3﹣10y，∴所求反函数是y=3﹣10x，x∈[0，lg2]．23．【答案】（1）详见解析；（2）详见解析.24．【答案】【解析】（本题满分为12分）解：（1）∵cos2A﹣3cos（B+C）﹣1=0．∴2cos2A+3cosA﹣2=0，…2分∴解得：cosA=，或﹣2（舍去），…4分又∵0＜A＜π，∴A=…6分（2）∵a=2RsinA=，…又∵a2=b2+c2﹣2bccosA=b2+c2﹣bc≥bc，∴bc≤3，当且仅当b=c时取等号，…∴S△ABC=bcsinA=bc≤，∴三角形面积的最大值为．…。

作者简介胡金飞（1983—），男，安徽庐江县人，高级工程师，主要从事白蚁防治研究工作。

收稿日期2022-11-25浅谈茯苓白蚁的危害及治理胡金飞（六安市白蚁防治中心，安徽六安237000）摘要真菌茯苓的干燥菌核是我国传统药食两用的大宗中药材，在其人工栽培过程中深受白蚁侵害。

本文总结了危害茯苓的白蚁主要种类，分析了白蚁危害茯苓的原因，并提出了茯苓白蚁的综合治理策略，以期为茯苓白蚁防治工作提供参考。

关键词茯苓；白蚁；危害；治理中图分类号S435.673文献标识号A文章编号1007-7731（2023）08-0144-04茯苓（Poria cocos ）属多孔菌科茯苓属，是一种以腐生为主的高等担子菌[1-2]。

野生茯苓广泛分布于中国、印度、日本等国[3]，我国黄河以南大部分省区均有分布[4]，多寄生于赤松（P.densiflora ）或马尾松（P.massoniana ）等松科植物根部，深入地下20~30cm [3]。

茯苓干燥的菌核即为被誉为中药“八珍”之一的茯苓，是我国传统药食两用的大宗中药材[1-2，5]，其应用范围广、用量大，有“十方九茯苓”之说。

我国是茯苓主产国，茯苓产业产值超过100亿元[6]，约占世界总产量的70%，我国干茯苓年需求量超3万t ，野生茯苓的数量早已不能满足市场需求，目前以人工栽培为主，主产于安徽、湖北、湖南、贵州、云南、浙江、福建、广东、广西、四川、重庆、河北、河南、山东、陕西、山西等地区。

道地药材茯苓的产地大多分布在山区，是当地的特色产业和农民增收的主导产业[3]。

白蚁是严重危害茯苓的主要害虫，一旦发生白蚁危害，轻则减产，重则绝收[7-11]，上述茯苓主要产区均有不同程度的白蚁危害[12]。

因此，白蚁防治是茯苓生产产业化的关键问题之一，做好茯苓的白蚁防治工作是促进茯苓种植增产增收的重要举措。

1茯苓白蚁的危害情况1.1白蚁危害茯苓实例2007年5月和2008年6月，笔者在茯苓道地产区金寨县桃岭乡桐岗村、霍山县漫水河镇调查中药材白蚁危害情况时，发现培植基地的茯苓除了当年刚经药物处理过的培植菌材外，其余的均不同程度遭受白蚁危害，有的一窖苓木被白蚁蛀食一空，且采集到的土白蚁（Odontotermes ）兵蚁个体大小差异明显，可能来自于不同群体。