12 大学物理动量矩定理
- 格式:ppt
- 大小:3.43 MB
- 文档页数:82


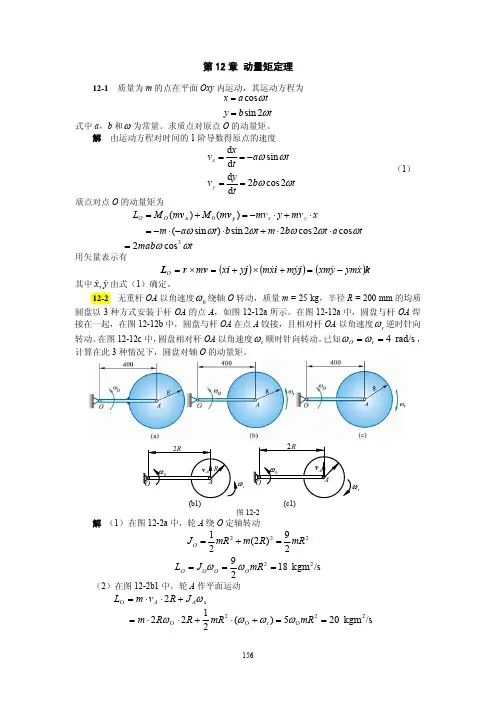

动量矩定理的三个公式动量矩定理是物理学中的重要概念,它有三个关键公式。
这三个公式在解决许多物理问题时,那可是相当有用的。
咱们先来聊聊第一个公式:对某定点 O,质点的动量矩 L 等于质点对该点的位置矢量 r 与质点的动量 p 的矢量积,即 L = r × p 。
这个公式看似有点复杂,其实你仔细琢磨琢磨,也不难理解。
比如说,你想象一下,有个小球在光滑的平面上滚动。
这个小球的速度很快,质量也不小。
那它的动量就比较大。
如果这个小球距离某个固定的点比较远,那它相对于这个点的动量矩就会更大。
再来说说第二个公式:质点所受的合力 F 对某定点 O 的力矩 M 等于质点对该点 O 的动量矩随时间的变化率,即 M = dL/dt 。
这个公式能帮助我们理解物体在受到外力作用时,它的转动状态是怎么变化的。
就像我们骑自行车的时候,我们蹬脚踏板的力就相当于一个外力。
这个力产生的力矩会让自行车的轮子转动起来,并且改变轮子的转动速度和方向。
最后是第三个公式:质点系对某定点 O 的动量矩 L 等于质点系中各质点对该点动量矩的矢量和,即L = ∑(ri × pi)。
这三个公式在实际应用中可是大显身手。
记得有一次,我在学校的物理实验室里,看到同学们在做一个关于转动惯量的实验。
实验台上有一个可以绕着中心轴旋转的圆盘,圆盘上有不同位置的小孔,可以通过改变小孔的位置来改变圆盘的质量分布。
同学们在圆盘上施加一个恒定的力矩,然后观察圆盘的转动情况。
他们通过测量圆盘的角速度和角加速度,来验证动量矩定理的公式。
当时有个同学怎么都弄不明白为什么改变圆盘的质量分布会影响它的转动状态。
我就用动量矩定理的公式给他解释。
我说,你看啊,质量分布变了,相当于质点的位置变了,那对中心点的动量矩也就跟着变了。
合力矩不变的情况下,动量矩的变化率就不一样了,所以转动状态就不同啦。
这同学听了之后,恍然大悟,那种因为搞懂一个难题而露出的兴奋表情,我到现在都还记得。






1质点系对某轴的动量矩等于质点系中各质点的动量对同一轴之矩的代数和。
( ) 2刚体的质量是刚体平动时惯性大小的度量,刚体对某轴的转动惯量则是刚体绕该轴转动时惯性大小的度量。
( ) 3刚体对某轴的回转半径等于其质心到该轴的距离。
( )4如果作用于质点系上的所有外力对固定点O 的主矩不为零,那么,质点系的动量矩一定不守恒。
( )5如果质点系所受的力对某点(或轴)的矩恒为零,则质点系对该点(或轴)的动量矩不变。
( ) 6图中所示已知两个均质圆柱,半径均为R ,质量分别为2m 和3m ,重物的质量为1m 。
重物向下运动的速度为V ,圆柱C 在斜面上只滚不滑,圆柱O 与绳子之间无引对滑动,则系统对O 轴的动量矩为vR m R m vR m H o 12232++=ω。
( )7图中已知均质圆轮的半径为R ,质量为m ,在水平面上作纯滚动,质心速度为C v,则轮子对速度瞬心I 的动量矩为R mv H c I =。
( )1已知刚体质心C 到相互平行的z z 、'轴的距离分别为b a 、,刚体的质量为m ,对z 轴的转动惯量为z J ,则'z J 的计算公式为__________________。
A .2)(b a m z z ++='J J ;B .)(22b a m z z -+='J J ; C.)(22b a m z z --='J J 。
2两匀质圆盘A 、B ,质量相等,半径相同,放在光滑水平面上,分别受到F 和'F 的作用,由静止开始运动,若'F F =,则任一瞬间两圆盘的动量相比较是_____________________。
A.B A p p >; B.B A p p <; C.B A p p =。
3在一重W 的车轮的轮轴上绕有软绳,绳的一端作用一水平力P ,已知车轮的半径为R ,轮轴的半径为r ,车轮及轮轴对中心O 的回转半径为ρ,以及车轮与地面间的滑动摩擦系数为f ,绳重和滚阻皆不计。
动量矩定理公式
动量矩定理公式是描述物体运动状态的基本定律之一,它是在牛顿第二定律的基础上发展起来的。
根据动量矩定理公式,物体的运动状态可以用动量和矩来描述。
其中,动量是物体的质量和速度的乘积,矩则是力对物体作用的力臂乘积。
动量矩定理公式可以表示为:动量矩 = 力矩,即动量矩守恒。
在物理学中,动量矩定理公式被广泛应用于解决物理问题,特别是在机械运动和力学领域。
通过对动量矩定理公式的分析,我们可以了解物体运动状态的变化过程,分析物体的动量和角动量,探究运动与力学的基本关系。
同时,动量矩定理公式也为工程设计、车辆运动控制、机器人技术等领域提供了理论支持。
简而言之,《动量矩定理公式》是描述物体运动状态的基本定律之一,它将动量和矩联系在了一起,为我们提供了解决物理问题的基本工具。
- 1 -。