012 第十二章 动量矩定理
- 格式:doc
- 大小:5.46 MB
- 文档页数:30






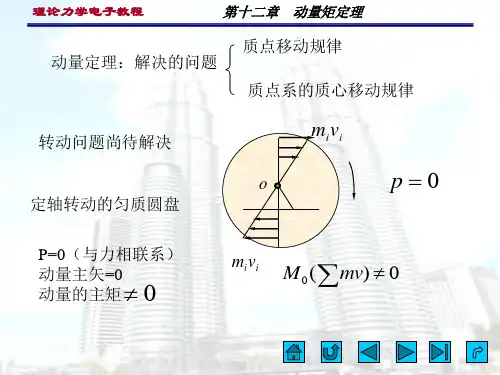




第十二章 动量矩定理§12—1 质点和质点系的动量矩一、质点的动量矩质点Q 的动量对于点O 的矩,定义为质点对于点O 的动量矩动量矩的单位:kgm 2/s二、 质点系的动量矩()mvr mv M O ⨯=()OQAr mv mv M O ∆=∙=2sin ϕ()i i ni O O v m M L ∑==1()i i nz z v m M L ∑=()A Q O mv M z ''∆±=2()[]()mv M mv M z z O =绕定轴转动刚体对其转轴的动量矩等于刚体对转轴的转动惯量与转动角速度的乘积。
§12—2 动量矩定理一、质点的动量矩定理质点的动量矩定理: 质点对某定点的动量矩对时间的一阶导数,等于作用力对同一点的矩。
直角坐标投影式为[]zz O L L =()2111i ni i i ni i i i i ni z z r m r v m v m M L ∑∑∑====∙==ω21i ni i z r m J ∑==ωz z J L =()mv dtdr mv dt dr mv r dt d mv M dt d O ⨯+⨯=⨯=)()(()F r mv v mv M dtdO ⨯+⨯=()()F M mv M dtdO O =()()()()()()F M m v M dtdF M m v M dt dF M m v M dt dz z y y x x ===特殊情形:当质点受有心力F 的作用时,如图11-4所示,力矩0=)(o F M ,则质点对固定点O 的动量矩)(m o v M =恒矢量,质点的动量矩守恒。
例如行星绕着恒星转,受恒星的引力作用,引力对恒星的矩0=)(o F M ,行星的动量矩)(m o v M =恒矢量,此恒矢量的方向是不变的,因此行星作平面曲线运动;此恒矢量的大小是不变的,即mvh =恒量,行星的速度v 与恒星到速度矢量的距离h 成反比。
第12章 动量矩定理通过上一章的学习我们知道动量是表征物体机械运动的物理量。
但是在某些情况下,一个物体的动量不足以反映它的运动特征。
例如,开普勒在研究行星运动时发现,行星在轨道上各点的速度不同,因而动量也不同,但它的动量的大小与它到太阳中心的距离之乘积—称为行星对太阳中心的动量矩,总是保持为常量,可见,在这里,行星对太阳中心的动量矩比行星的动量更能反映行星运动的特征。
在另一些情况下,物体的动量则完全不能表征它的运动。
例如,设刚体绕着通过质心C 的z 轴转动。
因为不论刚体转动快慢如何,质心速度C v总是等于零,所以刚体的动量也总是零。
但是,刚体上各质点的动量大小与其到z 轴的距离的乘积之和—即刚体对z 轴的动量矩却不等于零。
可见,在这里,不能用动量而必须用动量矩来表征刚体的运动。
§12-1 质点动量矩定理例2.人造地球卫星本来在位于离地面600km h =的圆形轨道上,如图所示,为使其进入410km r =的另一圆形轨道,须开动火箭,使卫星在A 点的速度于很短时间内增加0.646km/s ,然后令其沿椭圆轨道自由飞行到达远地点B ,再进入新的圆形轨道。
问:(1)卫星在椭圆轨道的远地点B 处时的速度是多少?(2)为使卫星沿新的圆形轨道运行,当它到达远地点B 时,应如何调整其速度?大气阻力及其它星球的影响不计。
地球半径6370km R =。
图12-5解:首先求出卫星在第一个圆形轨道上的速度,可由质点动力学方程求出。
卫星运行时只受地球引力的作用,即22()R F mg R x =+ 式中x 是卫星与地面的距离。
当卫星沿第一圆形轨道运动时,有222()()v R m mgR h R h =++ 即22()gR v R h =+ (b )将6370km R =,600km h =,9.8m/s g =代入上式,得卫星在第一个圆形轨道上运动的速度17.553km/s v = 所以卫星在椭圆轨道上的A 点的速度为7.5530.6468.199km/s A v =+=卫星在椭圆轨道上运动时,仍然只受地球引力作用,而该引力始终指向地心O ,对地以O 的矩等于零,所以卫星对地心O 的动量矩应保持为常量。
设卫星在远地点B 的速度为B v ,则有A AB B r v r v = 所以463706008.199 5.715km/s 10A B A B r v v r +=⨯=⨯= 设卫星沿新的圆形轨道运行时所需的速度为2v ,则222249.86370 6.306km/s 10gR v r ⨯=== 由此可见,为使卫星沿着第二个圆形轨道运行,当它沿椭圆轨道到达B 点时,应再开动火箭,使其速度增加一个值 20.591km/s B B v v v ∆=-=顺便指出,在(b )式中令0h →,就得到7.9km/s v =,这就是为使卫星在离地面不远处作圆周运动所需的速度,称为第一宇宙速度。
§12-2 质点系动量矩定理例1.质量为1m 、半径为R 的均质圆轮绕定轴O 转动,如图所示。
轮上缠绕细绳,绳端悬挂质量为2m 的物块,试求物块的加速度。
均质圆 轮对于O 轴的转动惯量为2112O J m R =。
图12-8解:以整个系统为研究对象,先进行运动分析。
设在图示瞬时,物块的速度为v ,加速度为a ,由运动学关系,圆轮的角速度为/v R ω=, 因此系统的动量矩为2212121122O O v L J m vR m Rm vR m m vR R ω⎛⎫⎛⎫=--=-+=-+ ⎪ ⎪⎝⎭⎝⎭再进行受力分析。
系统所受外力如图所示,其中1m g 、2m g 为主 动力,Ox F 、Oy F 为轴O 处的约束力。
根据动量矩定理()()e OO i dL m dt=∑F 有12212d m m vR m gR dt⎛⎫+ ⎪⎝⎭-=- 即12212m m Ra m gR ⎛⎫-+=- ⎪⎝⎭得物块的加速度21222m a g m m =+例 2.高炉运送矿石的卷扬机如图所示。
已知鼓轮为均质圆盘,半径为R ,重为P 。
在铅垂平面内绕水平轴O 转动。
小车和矿石总重为Q ,作用在鼓轮上的力矩为M ,轨道的倾角为α。
绳的重量及各处 的摩擦忽略不计,求小车的加速度。
均质圆盘对O 轴的转动惯量212O P J R g=。
图12-9解:研究对象:小车及鼓轮系统。
系统所受的外力有:力矩M ,重力P 、Q ,轴承反力O X 、O Y ,轨道的反力N ,这些力对转轴O 的矩为()()sin cos e O O i M m M Q R Q l Nl αα==-+⋅-⋅-∑F 因为cos N Q α=所以sin O M M Q R α=-+⋅运动分析:设鼓轮绕O 轴转动的角速度为ω,小车作直线运动的速度为v ,显然v R ω=,则系统对转轴O 的动量矩为O O QL J vR gω⎛⎫=-+ ⎪⎝⎭将212O P J R g=,v R ω=代入上式得()122O L P Q Rv g=-+ 由质点系动量矩定理 OO dL M dt= 得()12sin 2d P Q Rv M Q R dt g α⎡⎤-+=-+⋅⎢⎥⎣⎦可解得小车的加速度2(sin )()dv M QR a g dt P Q Rα-==+ 例3.水涡轮转子以匀角速ω绕铅垂轴z 转动,试求从涡轮叶片间流过的水流给涡轮机转子的转动力矩。
图12-10解:设Q 为单位时间内流过整个涡轮转子的水流的体积,即总流量。
水流的质量密度为ρ,涡轮进口AB 和出口DC 处的半径分别为1r 和2r ,进口与出口处的水流的绝对速度分别为1v 和2v,方向分别与轮缘切线方向成夹角1α和2α。
水流作用在涡轮转子上的转矩与转子给水流的反力矩z M '大小相等而转向相反。
取两叶片之间的流体为研究的质点系。
水在叶片中流运时,由于叶片的作用,质点系对转轴的动量矩将随时间而变化。
设在瞬时t ,两叶片间的流体占有体积为ABCD 。
而在瞬时t t +∆,水流流至abcd ,设水的流动是定常的,则公共容积abCD 内流体的动量矩保持不变。
因此,在t ∆时间内两叶片之间流体动量矩的变化为()()z z z abcd ABCD l l l ∆=-()()()()z z z z abCD CDcd ABab abCD l l l l ⎡⎤⎡⎤=+-+⎣⎦⎣⎦ ()()z z CDcd ABab l l =- 令两叶片间水的流量为q ,则222111(cos )(cos )z l q t v r q t v r ραρα∆=∆-∆ 222111(cos cos )q t v r v r ραα=∆-可得到在t ∆时间内流过整个涡轮转子的水流的动量矩变化为()222111(cos cos )z z L l q t v r v r ραα∆=∆=∆-∑∑222111(cos cos )Q t v r v r ραα=∆-水流受到的外力有重力和转子叶片的反力,其中重力与Oz 平行,其力矩为零,故只有转子上叶片给水流的反力矩z M '。
根据质点系动量矩定理zzdL M dt'= 可得2221110lim (cos cos )z z z t dL LM Q v r v r dt tραα∆→∆'====-∆ 而水流作用在涡轮上的力矩111222(cos cos )z z M M Q v r v r ραα'=-=-上式称为欧拉涡轮方程。
它表明在定常流动时,转矩只同进口与出口处水流的绝对速度有关。
例4.一半径为r ,重为1W 的均质水平圆形转台,可绕通过中心O 并垂直于台面的铅直轴转动。
重2W 的物块A 按规律2/2s at =沿台的边缘运动。
开始时,圆台是静止的。
求物块运动以后,圆台在任一瞬时 的角速度与角加速度。
均质水平圆台对O 轴的转动惯量为2112O W J r g=。
图12-11解:研究对象:转台及物块A 质点系统受力分析:转台重力1W ,物块重2W ,约束力O X ,O Y ,对铅垂轴取矩和始终为零,质点系对转轴的动量矩守恒,即O L =常数,因系统初始静止,故有0O L =由22at s =对时间求导可得r ds v at dt ==,设转台的角速度为ω,则由点的合成运动理论 a e r =+v v v 可得 a v at r ω=-则任一瞬时系统对转轴的动量矩为 2211()02O W W L at r r r g gωω=-⋅-= 则可得()22122aW t W W r ω=+将上式对时间求导则可得转台角加速度 ()22122aW W W r ε=+例5.均质鼓轮重1P ,半径为R ,对转轴的回转半径为ρ,在半径为r 的轴颈上绕一不可伸长的细绳,绳端系一重为2P 的重物,可变形的细绳简化一弹性刚度系数为k 的弹簧绕于轮缘上,试列写系统的运 动微分方程。
均质鼓轮对O 轴的转动惯量为21O P J gρ=。
解:研究对象:整个系统。
受力分析:如图所示,静止时系统处于平衡。
运动分析:定轴转动+平动,取鼓轮转角坐标ϕ,并取系统静平衡时转角坐标0ϕ=。
设系统静平衡时鼓轮静转角为s ϕ,则由静平衡方程()0O i m =∑F 22s k R P r ϕ= 再由质点系对固定轴的动量矩定理图12-12()0()e O i dL m dt=∑F 即有222122()s P P d r kR P r dt g g ρϕϕϕ⎡⎤⎛⎫+=-++⎢⎥⎪⎝⎭⎣⎦整理为222120P P r kR gg ρϕϕ⎛⎫++=⎪⎝⎭ 为一单自由度无阻尼的振动方程。
§12-3 刚体对轴的转动惯量.平行移轴定理例3.如图所示的钟摆,已知均质细杆质量为1m ,杆长为l ,均质圆盘的质量2m ,直径为d ,图示位置时摆的角速度为ω。
试求摆对于通过O 点的水平轴的动量矩。
图12-18解:本题先用组合法计算摆对于水平轴O 的转动惯量,即 O O O J J J =+杆盘 其中 211=3O J m l 杆而圆盘对于轴O 的转动惯量O J 盘可用平行轴定理计算22222212222O C d d d J J m l m m l ⎛⎫⎛⎫⎛⎫=++=++ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭盘盘 22238m d l ld ⎛⎫=++ ⎪⎝⎭得 222121338O J m l m d l ld ⎛⎫=+++ ⎪⎝⎭于是摆对于水平轴O 的动量矩为222121338O O L J m l m d l ld ωω⎡⎤⎛⎫==+++ ⎪⎢⎥⎝⎭⎣⎦例4 直径为R ,质量为m 的均质圆盘,在离圆心/3R 处挖去一半 径为/3r R =的圆,如图所示,试求其对于A 轴的转动惯量。
图12-19解:把该物体看成由半径分别为R 及r 的两个均质圆盘组成,设这两个圆盘的质量分别为1m 和2m ,它们对轴A 的转动惯量1A J 、2A J ,则物体对轴A 的转动惯量为12A A A J J J =-由于 22211111322A J m R m R m R =+=2222222217()26A J m r m R r m R =++=得 22123726A J m R m R =-因/3r R =,故2/9m m =,1m m =。