第三章立体的投影习题课
- 格式:ppt
- 大小:1.65 MB
- 文档页数:20



2019届九年级数学下册第三章3.1 投影练习(新版)湘教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(2019届九年级数学下册第三章3.1 投影练习(新版)湘教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为2019届九年级数学下册第三章3.1 投影练习(新版)湘教版的全部内容。
第3章投影与视图3.1 投影知识点1 平行投影1.平行投影中的光线是(A)A.平行的B.不平行的C.聚成一点的D.向四周发散的2.下列投影是平行投影的是(A)A.太阳光下窗户的影子B.台灯下书本的影子C.在手电筒照射下纸片的影子D.路灯下行人的影子3.下列图中是太阳光下形成的影子的是(A)4.一木杆按如图所示的方式直立在地面上,请在图中画出它在阳光下的影子.(用线段AB表示)解:如图.知识点2 中心投影5.下列哪种影子不是中心投影(D)A.皮影戏中的影子B.晚上在墙上的手影C.舞厅中霓虹灯形成的影子D.林荫道上的树影6.如图,晚上小亮在路灯下散步,他从A处向着路灯灯柱方向径直走到B处,这一过程中他在该路灯灯光下的影子(A)A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短7.画出如图中各木杆在灯光下的影子.解:如图.线段AB,A′B′是两根木杆的影子.知识点3 正投影8.如图,按照箭头所指的投影方向,图中圆柱的正投影是(B)A.圆B.矩形C.梯形D.圆柱9.(教材P99习题T4变式)画出如图物体(正三棱柱)的正投影:(1)投影线由物体前方射到后方;(2)投影线由物体左方射到右方;(3)投影线由物体上方射到下方.解:中档题10.正方形的正投影不可能是(D)A.正方形B.长方形C.线段D.梯形11.下图表示一块三角尺在光线照射下形成的投影,其中(2)是平行投影;(1)是中心投影;(3)是正投影.(1)(2) (3)12.如图分别是两棵树及其影子的情形.图甲图乙(1)哪个图反映了阳光下的情形?哪个图反映了路灯下的情形?(2)请画出图中表示小丽影长的线段;(3)阳光下小丽影子长为1。

湘教版九年级下册数学第3章投影与视图含答案一、单选题(共15题,共计45分)1、如图所示的几何体的俯视图是()A. B. C. D.2、用6个完全相同的小正方体组合成如图所示的立体图形,它的左视图为()A. B. C. D.3、图①是由一个完全相同的小正方体组成的立体图形,将图①中的一个小正方体改变位置后如图②,则三视图发生改变的是()A.主视图,俯视较和左视图都改变B.左视图C.俯视图D.主视图4、如图,共有12个大不相同的小正方形,其中阴影部分的5个小正方形是一个正方体的表面展开图的一部分.现从其余的小正方形中任取一个涂上阴影,则能构成这个正方体的表面展开图的概率是()A. B. C. D.5、如图是一无盖的正方体盒子,其展开图不能是()A. B. C. D.6、如图,墨水瓶的瓶盖和瓶身都是圆柱形,则它的俯视图是A. B. C. D.7、由大小相同的正方体木块堆成的几何体的三视图如右图所示,则该几何体中正方体木块的个数是( )A.6个B.5个C.4个D.3个8、如图所示的正方体展开后的平面图形是( )A. B. C. D.9、如图,一个放置在水平实验台上的锥形瓶,它的俯视图为()A. B. C. D.10、如图,这是由5个大小相同的小正方体摆成的立体图形,它的俯视图是()A. B. C. D.11、下列几何体的主视图是三角形的是()A. B. C. D.12、一个几何体由大小相同的小正方体搭成,从上面看到的几何体的形状图如图所示,其中小正方形中的数字表示在这个位置小正方体的个数.从左面看到的这个几何体的形状图的是()A. B. C. D.13、如图所示的几何体的左视图是()A. B. C. D.14、由5个完全相同的正方体组成的几何体的主视图是()A. B. C. D.15、下列几何体中,侧面展开图可能是正方形的是()A.正方体B.圆柱C.圆锥D.球体二、填空题(共10题,共计30分)16、在数学活动课上,老师带领数学小组测量大树的高度.如图,数学小组发现大树离教学楼有5m,高1.4m的竹竿在水平地面的影子长1m,此时大树的影子有一部分映在地面上,还有一部分映在教学楼的墙上,墙上的影子离为2m,那么这棵大树高________m.17、如图,长方形 ABCD 的长 AB=4,宽 BC=3,以 AB 所在的直线为轴,将长方形旋转一周后所得几何体的主视图的面积是________.18、如图所示,该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上,于是他们开展了测算小桥所在图的半径的活动.小刚身高1.6米,测得其影长为2.4米,同时测得EG的长为3米,HF的长为1米,测得拱高(弧GH的中点到弦GH的距离,即MN的长)为2米,则小桥所在圆的半径为________ m19、一个几何体是由许多规格相同的小正方体堆积而成的,其主视图、左视图如图所示,要摆成这样的几何体,至少需用________个正方体,最多需用________个正方体;20、如图是一个几何体的三视图,根据图示的数据可计算出该几何体的表面积为________.21、如图,一个正方体,6个面上分别写着6个连续的整数,且每个相对面上的两个数之和相等,如图所示,你能看到的数为9、12、13,则六个整数之和为________.22、某数学兴趣小组利用太阳光测量一棵树的高度(如图),在同一时刻,测得树的影长为4.8米,小明的影长为1.2米,已知小明的身高为1.5米,则树高为________ 米.23、一张桌子摆放若干碟子,从三个方向上看,三种视图如图所示,则这张桌子上共有________个碟子.24、如图是由一些相同的小正方体构成的立体图形的三种视图,那么构成这个立体图形的小正方体有________ 个.25、某几何体的三视图如图所示,则组成该几何体的小正方体的个数是________三、解答题(共5题,共计25分)</span>26、由大小相同的5个小立方块搭成的几何体如图所示,请在方格中画出该几何体从上面和左面看到的形状图(用黑色笔将虚线画为实线).27、已知一个几何体的三视图和有关的尺寸如图所示,请写出该几何体的名称,并根据图中所给的数据求出它的表面积和体积.28、一个几何体的三视图如图所示,已知主视图、左视图和俯视图如图所示.(1)请说出这个几何体的名称;(2)根据图中给出的数据(单位:分米),求这个几何体的侧面积.29、小刚的桌上放着两个物品,它的三视图如图所示,你知道这两个物品是什么吗?30、如图所示的平面图形折叠成正方体后,相对面上的两个数之和为10,求的值.参考答案一、单选题(共15题,共计45分)1、D3、D4、D5、C6、A7、C8、D9、B10、A11、B12、B13、D14、A15、B二、填空题(共10题,共计30分)16、17、18、19、20、21、22、24、25、三、解答题(共5题,共计25分)26、27、28、29、30、。
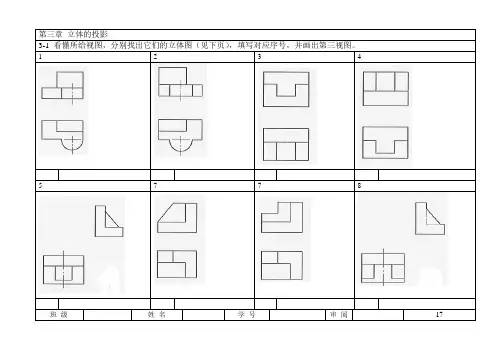
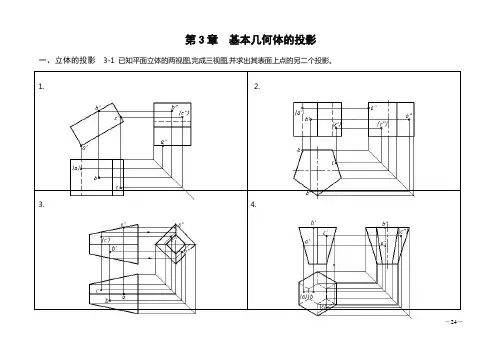
3-1 看懂所给视图,分别找出它们的立体图(见下页),填写对应序号,并画出第三视图。
1 2 3 45 7 7 8班级姓名学号审阅171 2 3 46 7 89 10 11 12 班级姓名学号审阅18第三章立体的投影3-2 求作体的第三视图,并补全立体表面上点的其余两投影。
1 2 34 5 6班级\ 姓名学号审阅193-3 求作第三视图1 2 34 5 6班级姓名学号审阅203-4 求作左视图,并用彩色笔勾画平面P的三面投影。
3-5 求作俯视图,并用彩色笔勾画出Q面的三面投影。
班级姓名学号审阅213-6 补全下列切割体的投影。
1 23 41 2班级姓名学号审阅223-7补全下各组视图中所缺的漏线或第三视图。
1 23 4班级姓名学号审阅233-8 已知主视图和俯视图,选择正确的左视图。
1 2 3 43-9 已知主视图和俯视图,选择正确的左视图。
1 2 3 4班级姓名学号审阅243-10 完成复合回转体截交线的三面投影。
1 2班级姓名学号审阅253-11 求出立体图表面的相贯线。
1 23 4班级姓名学号审阅263-12 求作主视图。
3-13 求作俯视图。
3-14 求作主视图。
3-15 求作俯视图。
班级姓名学号审阅273-16 求出立体表面的相贯线。
1 23 4班级姓名学号审阅283-17 已知主视图和俯视图,选择正确的左视图。
1 2 3 43-18 已知主视图和俯视图,选择正确的主视图。
1 2 3 4班级姓名学号审阅293-19 用辅助平面法补全主视图和俯视图上所缺的线。
班级姓名学号审阅303-20 根据已知图画正等轴测图。
3-21 根据已知视图画正等轴测图及斜二轴测图。
班级姓名学号审阅31。



九年级数学下册第3章投影与三视图3.1 投影第2课时中心投影同步练习(新版)浙教版编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(九年级数学下册第3章投影与三视图3.1 投影第2课时中心投影同步练习(新版)浙教版)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为九年级数学下册第3章投影与三视图3.1 投影第2课时中心投影同步练习(新版)浙教版的全部内容。
第3章三视图与表面展开图3.1 投影第2课时中心投影知识点1 中心投影的理解1.下列属于中心投影的有( )①台灯下笔筒的影子;②房后的荫凉;③美术课上,灯光下临摹用的静物的影子;④房间里花瓶在灯光下的影子;⑤在空中低飞的老鹰在地上的影子.A.5个 B.4个 C.3个 D.2个2.如图3-1-6,晚上小亮在路灯下散步,在小亮由A处走到B处这一过程中,他图3-1-6在地上的影子( )A.逐渐变短B.逐渐变长C.先变短后变长D.先变长后变短3.下面四幅图中,灯光与影子的位置最合理的是()图3-1-7知识点2 关于中心投影作图4.如图3-1-8,小华、小军和小丽同时站在路灯下,其中小军和小丽的影子分别是AB,CD。
(1)请你在图中画出路灯灯泡所在的位置(用点P表示);(2)画出小华此时在路灯下的影子(用线段EF表示).图3-1-8图3-1-95.圆桌面(桌面中间有一个直径为0。
4 m的圆洞)正上方的灯泡(看作一个点)发出的光线照射平行于地面的桌面后,在地面上形成如图3-1-9所示的圆环形阴影.已知桌面直径为1.2 m,桌面离地面1 m,若灯泡离地面3 m,则地面圆环形阴影的面积是()A.0.324π m2 B.0.288π m2C.1.08π m2 D.0.72π m26.在直角坐标系中,一点光源位于点(0,4)处,点P的坐标为(3,2),则点P在x轴上的投影的坐标为________.7.如图3-1-10,王琳同学在晚上由路灯A走向路灯B,当他行到P处时发现,他在路灯B下的影长为2米,且影子顶部恰好位于路灯A的正下方,接着他又走了6.5米到Q处,此时他在路灯A下的影子顶部恰好位于路灯B 的正下方(已知王琳的身高为1。

工程制图基础哈尔滨工业大学习题答案课后答案网第一章 制图的基本知识第二章 点、直线和平面的投影第三章 立体第四章 平面与曲面立体相交、两曲面立体相交第五章 轴测图第六章 组合体第七章 机件的表达方法第八章 标准件与常用件第九章 零件图课后答案网第一章 制图的基本知识习题 1-6习题 1-7习题 1-8习题 1-9返回习题 1-10习题 1-11课后答案网第一章 制图的基本知识1-6 尺寸注法。
(1)注出各方向的尺寸(2)注出角度(3)注出直径(4)注出半径课后答案网1-7 尺寸注法(按1:1测量取整数)。
网案答后课1-8 几何作图(1)作正六边形(外接圆φ70)(2)作五角星(外接圆φ60)网案答后课1-9 几何作图 作带斜度和锥度的图形,并标注网案答后课第一章 制图的基本知识1-10 已知椭圆长轴为70,短轴为45,作椭圆(1) 同心圆法(2) 四心圆弧法第一章 制图的基本知识1-11 按给出的图形及尺寸,完成下面的作图网案答后课第二章 点、直线和平面的投影习题 2-1习题 2-2习题 2-3习题 2-4习题 2-5习题 2-6习题 2-7习题 2-8习题 2-9习题 2-10习题 2-11习题 2-12习题 2-13习题 2-14习题 2-15习题 2-16习题 2-17习题 2-18习题 2-19习题 2-20返回课后答案网2-1 根据立体图画点的投影图(按1:1量取)(1) (2)网案答后课2-2 根据点的坐标画出其投影图和立体图A(15,10,25),B(25,15,20),(15,15,20)(1) M(10,15,20),(20,0,25),(10,20,20)(2)课后答案网2-3 根据点的两面投影作第三面投影,并比较各点的相对位置左后下 下 上C 后右B 前左B、C、D和A比较在A点的上下在A点的前后在A点的左右在A点的左右在A点的前后后下 左右后下 DC B 在A点的上下B、C和A比较(2)(1)课后答案网2-4 补画出直线的第三投影,并判断是什么位置直线(7)(6)(5)(8)(4)(3)(2) (1)一般位置侧垂水平铅垂侧垂正垂侧平正平线线线线线线线线课后答案网2-5 补画出三棱锥的侧面投影,并判断各棱线是什么位置直线一般一般一般一般正平正垂侧垂侧平水平水平一般一般( )cabscbsa OOXc b abY HcasWY Zs线线线线线线SASB SC AC BCAB 线BC线AC 线AB 线SC 线SB SA BCSA sscac (2)线abb(1)HWY Y ZX课后答案网2-6 根据所给的条件作出直线的三面投影Z Y Y WH(1)OXY HOYZXY HOZXY HOZ(2)(3)(4)Y WY Wa′aaa′a′abbbaaabbb ab b(a )b abbb已知线段点A(30,10,10),点B(10,20,25)。
[作图题][难度1]1、求作属于圆柱表面的点A、B、C、D 的另外两面投影。
[参考答案][作图题][难度2]2、补全正五棱柱的水平投影,并画出属于棱柱表面的点A、B及线段CD的其他两面投影。
[参考答案][作图题][难度3]3、补画出正六棱台的侧面投影,并补全属于棱台表面的线段AB、BC、CD的其他两面投影。
[参考答案][作图题][难度3]4、画出半圆柱的水平投影。
并求作属于圆柱表面的曲线AB的另外两面投影[参考答案][作图题][难度2]5、求作属于圆锥表面的点A、B、C、D的另外两面投影。
[参考答案][作图题][难度3]6、画出圆锥的侧面投影。
并求作线段SB、BC的另外两面投影。
[参考答案][作图题][难度2]7、画出圆球的水平投影和侧面投影,并求作属于圆球表面的点A、B、C、D的另外两面投影。
[参考答案][作图题][难度3]8、求作属于圆球表面的曲线段的另外两面投影。
[参考答案][作图题][难度2]9、已知属于回转体表面的点A、B的一个投影,求作另外两面投影。
[参考答案][作图题][难度3]10、画全同轴回转体的正面投影和侧面投影,并补画其水平投影。
[参考答案][作图题][难度3]11、画出侧面投影图。
[参考答案][作图题][难度4]12、补全正五棱柱的水平投影和侧面投影。
[参考答案][作图题][难度4]13、补画带切口的正三棱锥的水平投影和侧面投影。
[参考答案][作图题][难度3]14、画出圆柱体被截切后的侧面投影。
[参考答案][作图题][难度3]15、画出圆锥体被截切后的侧面投影。
[参考答案][作图题][难度3]16、画出圆球体被截切后的水平投影和侧面投影。
[参考答案][作图题][难度4]17、画出侧面投影。
[参考答案][作图题][难度3]18、求作侧面投影。
[参考答案][作图题][难度2]19、画全长方体与圆柱相交的正面投影图和水平投影图。
[参考答案][作图题][难度3]20、补全正面投影。
初二数学下册立体形的投影与展开练习题1. 立体形的投影在几何学中,立体形的投影是指立体形在一个平面上的影射。
通过立体形的投影,我们可以更直观地理解和研究立体形的特征和属性。
2. 立体形的展开立体形的展开是指将一个立体形完全展开成一个平面图形。
通过立体形的展开,我们可以更方便地计算和测量立体形的各种特征。
接下来,我们将通过一些练习题来巩固和应用我们对立体形的投影与展开的理解。
练习题1:长方体的投影与展开将一个长方体投影到一个平面上,并将该长方体展开成一个平面图形。
解答:首先,将长方体投影到一个平面上。
假设长方体的顶点分别为ABCDEFGH,我们选择平面上的一个点O为投影中心点。
接下来,我们需要确定每个顶点的投影位置。
A点的投影位置为A',连接OA和OA',OA'的长度为AA'。
B点的投影位置为B',连接OB和OB',OB'的长度为BB'。
其他顶点的投影位置的计算方式类似。
最终,我们可以得到长方体在平面上的投影。
接下来,我们将长方体展开成一个平面图形。
在展开的过程中,我们需要保持各个面之间的相对位置不变。
将长方体展开后,我们可以得到一个包含6个面的平面图形。
这个平面图形的形状与长方体的外表面相同,只是被打开展开了而已。
练习题2:正方体的投影与展开将一个正方体投影到一个平面上,并将该正方体展开成一个平面图形。
解答:正方体是一个特殊的长方体,其六个面都是正方形。
首先,选择适当的投影中心点O。
然后,确定每个顶点的投影位置,连接各个顶点与其投影点,我们可以得到正方体在平面上的投影。
接下来,我们将正方体展开成一个平面图形。
同样地,保持各个面之间的相对位置不变。
展开后,我们可以得到一个由六个正方形构成的平面图形。
这个平面图形是正方体的展开形式。
练习题3:棱锥的投影与展开将一个棱锥投影到一个平面上,并将该棱锥展开成一个平面图形。
解答:棱锥是一个具有一条尖顶和一个多边形底面的立体形。