西安邮电大学信号与系统48学时总复习2014版
- 格式:ppt
- 大小:1.12 MB
- 文档页数:45


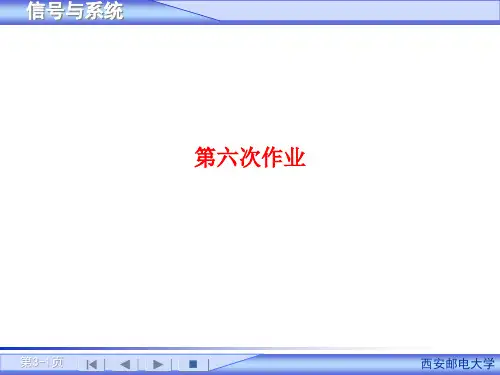


信号与系统西安邮电习题答案第一次1.1画出下列各个信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)解:正弦信号周期(2)解:,正弦信号周期(3)解:,正弦信号周期(4)(5)1.2画出下列各信号的波形[式中为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括和的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法: 首先考虑各信号中普通函数的波形特点,再考虑与或结合时的变化情况;若只是普通信号与阶跃信号相乘,则可利用或的性质直接画出或部分的普通函数的波形;若是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1)(2)(3)解:(4)(5)1.3写出下图所示各波形的表达式(1)解:(2)解:1.4写出下图所示各序列的闭合形式的表示式(a)解:(b)解:(课堂已讲)1.5判别下列各序列是否为周期性的,如果是,确定其周期(1)解:周期序列(2)解:,,m取3,;,,;故(3)解:,,故非周期;,,;故非周期 1.6已知信号的波形如下图所示,画出下列各函数的波形(1)(2)(3)1.7已知序列的图形如图所示,画出下列各序列的图形(1)(2)1.8信号的波形图如下所示,试画出和的波形解:由图可知:,则当时,;当时,当时,(课堂已讲)1.9已知信号的波形如图所示,分别画出和的波形解:第二次1.10计算下列各题,(1)解:(2)解:(3)解:(4)解:(5)解:(6)解:(7)解:(8)解:(课堂已讲)1.11设系统的初始状态为,激励为,各系统的全响应与激励和初始状态的关系如下,试分析各系统是否是线性的。

关于2013级课表以及F段教室
情况说明
各位任课教师:
因13级新生第七周开始上课,为按时完成教学计划,经研究决定,从第七周到第十八周每周六进行补课。
补课规则为从第七周周六开始,每周六按照周一至周五的教学计划依次进行补课,即第七周周六补周一的课程,第八周周六补周二的课程,依次顺延循环。
课表中教室号以F开头的教室,为东区新盖实验楼教室。
例如F0208:代表东区实验楼二楼208教室。
教务处
2013-07-01
新校区2013-2014学年第二学期电子工程学院本科课程表(十)
新校区2013-2014学年第一学期电子工程学院本科课程表(十三)
新校区2013-2014学年第一学期通信与信息工程学院本科课程表(二十二)。

信号与系统期末复习材料信号与系统期末复习一、基础知识点:1.信号的频带宽度(带宽)与信号的脉冲宽度成反比,信号的脉冲宽度越宽,频带越窄;反之,信号脉冲宽度越窄,其频带越宽。
2. 系统对信号进行无失真传输时应满足的条件:①系统的幅频特性在整个频率范围(∞<<∞-ω)内应为常量。
②系统的相频特性在整个频率范围内应与ω成正比,比例系数为-0t3.矩形脉冲信号的周期与频谱线的间隔存在着倒数的关系。
4.零输入响应(ZIR )从观察的初始时刻(例如t=0)起不再施加输入信号(即零输入),仅由该时刻系统本身具有的初始状态引起的响应称为零输入响应,或称为储能响应。
5.零状态响应(ZSR )在初始状态为零的条件下,系统由外加输入(激励)信号引起的响应称为零状态响应,或称为受迫响应。
6.系统的完全响应也可分为:完全响应=零输入响应+零状态响应7.阶跃序列可以用不同位移的单位阶跃序列之和来表示。
8.离散信号)(n f 指的是:信号的取值仅在一些离散的时间点上才有定义。
9.信号的三大分析方法:①时域分析法②频域分析法③复频域分析法10.信号三大解题方法⑴傅里叶:①研究的领域:频域②分析的方法:频域分析法⑵拉普拉斯:①研究的领域:复频域②分析的方法:复频域分析法⑶Z 变换:主要针对离散系统,可以将差分方程变为代数方程,使得离散系统的分析简化。
11.采样定理(又称为奈奎斯特采样频率)如果)(t f 为带宽有限的连续信号,其频谱)(ωF 的最高频率为m f ,则以采样间隔ms f T 21≤对信号)(t f 进行等间隔采样所得的采样信号)(t f s 将包含原信号)(t f 的全部信息,因而可()()()zi zs y t y t y t =+利用)(t f s 完全恢复出原信号。
12.设脉冲宽度为1ms ,频带宽度为KHz ms111=,如果时间压缩一半,频带扩大2倍。
13.在Z 变换中,收敛域的概念:对于给定的任意有界序列)(n f ,使上式收敛的所有z 值的集合称为z 变化的收敛域。
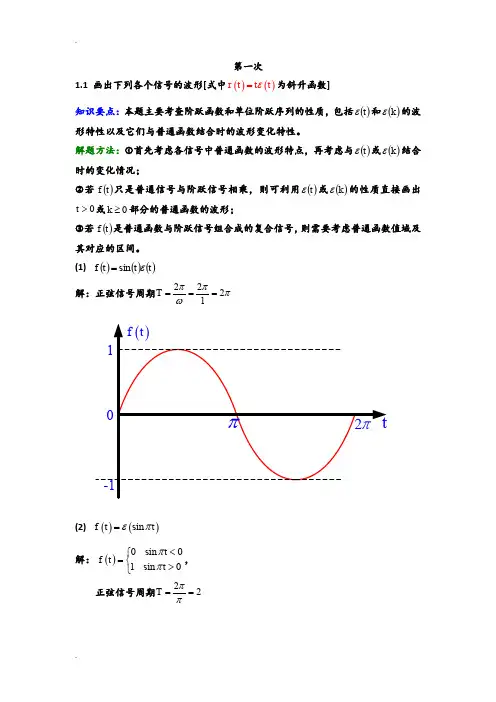
第一次1.1 画出下列各个信号的波形[式中()()r t t t ε=为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法:①首先考虑各信号中普通函数的波形特点,再考虑与()t ε或()k ε结合时的变化情况;②若()t f 只是普通信号与阶跃信号相乘,则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形;③若()t f 是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
(1) ()()()t t t f εsin = 解:正弦信号周期ππωπ2122===T 1-12ππt()f t(2) ()()sin f t t επ=解:()0 sin 01 sin 0t f t t ππ<⎧=⎨>⎩,正弦信号周期22==ππT10-1-1-212-1-2121()f t tt()sin t π(3) ()()cos f t r t =解:()0 cost 0cos cos 0f t t t <⎧=⎨>⎩,正弦信号周期221T ππ== 10-1t()cos t π2ππ-2π-1()f t 0tπ2ππ-2π-(4) ()()k k k f ε)12(+=-1-212k3135()f k …………(5) ()()()111k f k k ε+⎡⎤=+-⎣⎦-2-412k312()f k …………45-1-31.2 画出下列各信号的波形[式中()()r t t t ε=为斜升函数]知识要点:本题主要考查阶跃函数和单位阶跃序列的性质,包括()t ε和()k ε的波形特性以及它们与普通函数结合时的波形变化特性。
解题方法:①首先考虑各信号中普通函数的波形特点,再考虑与()t ε或()k ε结合时的变化情况;②若()t f 只是普通信号与阶跃信号相乘,则可利用()t ε或()k ε的性质直接画出0>t 或0≥k 部分的普通函数的波形;③若()t f 是普通函数与阶跃信号组合成的复合信号,则需要考虑普通函数值域及其对应的区间。
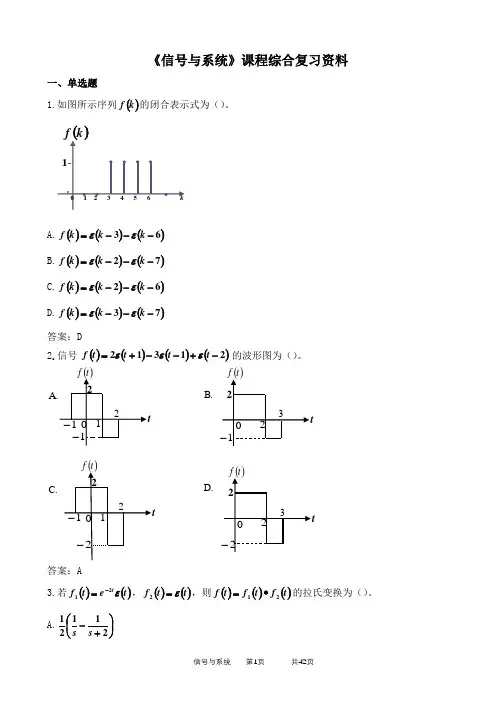
《信号与系统》课程综合复习资料一、单选题1.如图所示序列()k f 的闭合表示式为()。
A.()()()63---=k k k f εεB.()()()72---=k k k f εεC.()()()62---=k k k f εεD.()()()73---=k k k f εε 答案:D2.信号 的波形图为()。
答案:A3.若()()t e t f t ε21-=,()()t t f ε=2,则()()()t f t f t f 21*=的拉氏变换为()。
A.⎪⎭⎫ ⎝⎛+-21121s sA .B .C .D()()()()21312 -+--+=t t t t f εεεB.⎪⎭⎫⎝⎛-+s s 12121; C.⎪⎭⎫ ⎝⎛++21121s s D.⎪⎭⎫⎝⎛-+s s 12141 答案:A4.已知()t f 的波形如图所示,则()t f 的表达式为()。
A.()()()1--=t t t t t f εεB.()()()()()111----=t t t t t f εεC.()()()()11---=t t t t t f εεD.()()()()()111++-+=t t t t t f εε 答案:C5.信号()1f t 和()2f t 如图所示,()()()12f t f t f t =*,则()1f -等于()。
A.1B.1.5()t fC.-1D.-0.5 答案:B6.周期信号()t f 如图所示,其直流分量为()。
A.0B.4C.4.0D.2 答案:B7.已知某信号的拉氏变换()()s T e F s s αα-+=+,则该信号的时间函数为()。
A.()()t T e t T αε---B.()t e t T αε--C.()t e t αεα--D.()()t e t T ααε--- 答案:B8.()()0cos t t ωε的拉氏变换为()。
A.()()002πδωωδωω++-⎡⎤⎣⎦ B.()()00πδωωδωω++-⎡⎤⎣⎦ C.22s ωω+ D.220ss ω+答案:D9.()1)1(2++t e t ε的单边拉氏变换为()。

重难点1.信号的概念与分类按所具有的时间特性划分:确定信号和随机信号; 连续信号和离散信号; 周期信号和非周期信号; 能量信号与功率信号; 因果信号与反因果信号;正弦信号是最常用的周期信号,正弦信号组合后在任一对频率(或周期)的比值是有理分数时才是周期的。
其周期为各个周期的最小公倍数。
① 连续正弦信号一定是周期信号。
② 两连续周期信号之和不一定是周期信号。
周期信号是功率信号。
除了具有无限能量及无限功率的信号外,时限的或,∞→t 0)(=t f 的非周期信号就是能量信号,当∞→t ,0)(≠t f 的非周期信号是功率信号。
1.典型信号① 指数信号: ()at f t Ke =,a ∈R ② 正弦信号: ()sin()f t K t ωθ=+ ③ 复指数信号: ()st f t Ke =,s j σω=+ ④ 抽样信号: sin ()tSa t t= 奇异信号(1)单位阶跃信号1()u t ={ 0t =是()u t 的跳变点。
(2) 单位冲激信号单位冲激信号的性质: (1)取样性 11()()(0)()()()f t t dt f t t f t dt f t δδ∞∞-∞-∞=-=⎰⎰(0)t <(0)t >()1t dt δ∞-∞=⎰()0t δ=(当0t ≠时)相乘性质:()()(0)()f t t f t δδ=000()()()()f t t t f t t t δδ-=- (2)是偶函数 ()()t t δδ=- (3)比例性 ()1()at t aδδ=(4)微积分性质 d ()()d u t t tδ= ; ()d ()t u t δττ-∞=⎰(5)冲激偶 ()()(0)()(0)()f t t f t f t δδδ'''=- ;()()d (0)f t t t f δ∞-∞''=-⎰ ()d ()tt t t δδ-∞'=⎰ ;()()t t δδ''-=- ()d 0t t δ∞-∞'=⎰带跳变点的分段信号的导数,必含有冲激函数,其跳变幅度就是冲激函数的强度。

西 安 邮 电 学 院2014年招收攻读硕士学位研究生入学考试试题 考试科目代码及名称 824信号与系统A注:符号()t ε为单位阶跃函数,()k ε为单位阶跃序列,LTI 为线性时不变。
一、填空题(每空3分,共30分)1.积分102312d 2t e t t δ--⎛⎫--= ⎪⎝⎭⎰2.已知()(1)(2)h t t t εε=---,()(2)(4)f t t t εε=---,则卷积()()h t f t *=3.已知一离散LTI 系统的阶跃响应1()()2kg k k ε⎛⎫= ⎪⎝⎭,则该系统的单位序列响应()h k = 4.已知信号()f t 的波形如右图所示, 其傅里叶变换记为()F j ω,试求()d F j ωω∞-∞=⎰0(0)()F F j ωω===5.因果信号()f t 的单边拉普拉斯变换为()221()1s s e F s s --=+,则对应原函数的初值(0)f += ,终值()f ∞= 6.已知一连续系统的零、极点分布如右图 所示,()1H ∞=,则系统的系统函数 ()H s =7.对信号()()f t Sa t =进行均匀抽样的奈奎斯特抽样间隔s T =-28. 双边Z变换的象函数23()1132zF zz z,收敛域为1132z,则其对应的原序列()f k二、选择题(共10题,每题4分,共30分)1.周期序列3()cos cos4436f k k kππππ,其周期为()(A)8 (B)16 (C)24(D)482. 序列和2(2)kiiiδ等于()(A)4 (B)1 (C)4()kε(D)4(2)kε3. 信号()()tf t e tε的傅里叶变换()F jω等于()(A)11jω(B)11jω(C)11jω(D)11jω4. 如下图所示周期信号()f t,该信号不可能含有的频率分量是()(A)0.5Hz(B)1Hz(C)1.5Hz (D)2.5Hz5. 一个线性时不变的连续时间系统,其在某激励信号作用下的自由响应为3()t te e tε,强迫响应为21()te tε,则下面的说法正确的是()(A)该系统一定是二阶系统;(B)该系统一定是稳定系统;(C )零输入响应中一定包含3()tte e t ε;(D )零状态响应中一定包含21()tet ε。
华北电力大学2013~2014学年第 二 学期考试试卷(A )班级: 姓名: 学号:一.填空题(共20分) 1.0j j 0e [()()]d 1e t t t t t t ωωδδ∞---∞--=-⎰(1分)2. 判断如下所示系统是否具有线性、时不变性、因果性:()sin[()]()y t f t t ε= 非线性 , 时变 , 因果 。
(3分) 3. 连续周期信号傅里叶级数的两种形式011cos()n n n A A n t ωϕ∞=++∑,1j 1e n t n n F ω∞=∑(如果写指数形式和三角形式,也算对吧)。
(2分)4. 调制的实质是 频谱搬移 ,频分复用的关键是将信号与不同频率的 载波信号(三角信号) 相乘。
(2分)5. 序列0.5()[(2)(6)]t f t e t t εε-=---拉普拉斯变换的收敛域 整个s 平面 。
(2分)6. 连续因果系统的系统函数H (s )的零、极点分布图如图1-1所示,且H (∞)=1,则系统的冲激响应h (t ) = ()2()t t δε+。
(2分)图1-1 图1-27. 判断序列()sin(0.4)2cos(0.5)x k k k =π+是否具有周期性 否 ,若具有周期性则周期为 无 (若不具有周期性则写“无”)。
(2分)8. 图1-2所示的信号是功率信号还是能量信号 能量 ,其功率或能量为 0.5 。
(2分)9. 已知序列x (k )的Z 变换为2()(1)(2)z X z z z =--,则x (0)与x (1)为 1,3 。
(2分)10. 序列(2)(1)kk ε--+的单边Z 变换1212z z z---=。
(2分) 二.作图与简答(共30分)1. (6分)已知信号f (t )的波形如图2-1所示,画出(12)(1)f t t ε--的波形图。
2. (6分)f 1(t )与f 2(t )的波形如图2-2所示,作出f 1(t )*f 2(t )的波形。
精品文档信号与系复明 :以下出了大多数目的答案,答案是我个人做的,不保正确性,供参考 . 必把复弄明白并合复看 . 必每个同学!!!充要点 ( 必搞明白 ):1教材 p.185 例 6-12已知离散 LTI 系的位冲激响 h(n)= ⋯, 又已知入信号 x(n)= ⋯,系此的零状响h(n) 和 x(n) 的卷 .3 已知 LTI 系在入信号 f(t) 的零状响 y(t), 入信号 f(t) 的函数的零状响y(t) 的函数 ( 即入求 , 的零状响也求 )4教材 p.138 倒数第 3 行到 139 上半 , 理解并 , 必考 .一、单项选择题1.信号5sin 4t10cos3t 为( A)A. 周期、功率信号B.周期、能量信号C. 非周期、功率信号D.非周期、能量信号2.某连续系统的输入-输出关系为y(t ) f 2 (t ) ,此系统为( C)A. 线性、时不变系统B.线性、时变系统C. 非线性、时不变系统D.非线性、时变系统3.某离散系统的输入-输出关系为y(n) f (n) 2 f (n1) ,此系统为( A)A. 线性、时不变、因果系统B.线性、时变、因果系统C. 非线性、时不变、因果系统D.非线性、时变、非因果系统4. 积分t2)( t) dt 等于(B( t)0A. 2 (t )B.2u(t )C. u(t2)D. 2 ( t2)5. 分 e t(t3) dt 等于( C ) (此目必做 )A. e tB. e t(t3)C. e3D.06.下列各式中正确的是( B)A. 21B.(2t )1C.(2t)(t )D.(2 t )2(t ) (t )(2t )(t)227.信号f1(t ),f 2 (t ) 波形如图所示,设 f (t )f1(t)* f2 (t ) ,则 f (1)为(D)A.1B.2C.3D.4 8.已知 f(t)的波形如图所示,则f(5-2t)的波形为(C)9.描述某线性时不变连续系统的微分方程为y (t)3y(t)x(t ) 。