弹性力学-本构关系
- 格式:ppt
- 大小:1.01 MB
- 文档页数:21





本构关系1. 各向同性线性弹性本构方程及其中的物理常数G、λ、K 与E、μ的关系式;2. 球量和偏量的本构方程。
对于每一种材料,在一定的温度下,应力和应变之间有着完全确定的关系。
这是材料的固有特性,因此称为物理方程或者本构关系。
一般情况下,材料的应力与应变呈某一函数关系,可表示为:当式中的自变量:x、y、z、yz、zx、xy为小量时,可对其按Taylor级数展开,并略去二阶以上小量,如第一式,有上式中(f 1)0表达了函数f 1在应变分量为零时的值,根据应力应变的一般关系式可知,它代表了初始应力。
而表示函数f1 对应变分量的一阶偏导数,在小变形条件下,它们均为常数,这样可得一线性方程组:上述关系式是胡克(Hooke)定律在复杂应力条件下的推广,因此又称作广义胡克定律。
广义胡克定律中的系数Cmn(m,n=1,2,…,6)称为弹性常数,一共有36个,但可以证明,只有21个常数独立。
如果物体是非均匀材料构成的,物体内各点受力后将有不同的弹性效应,因此一般的讲,Cmn是坐标x,y,z的函数。
但是如果物体是由均匀材料构成的,那么物体内部各点,如果受同样的应力,将有相同的应变;反之,物体内各点如果有相同的应变,必承受同样的应力。
这一条件反映在广义胡克定理上,就是Cmn 为弹性常数。
对于完全的各向异性弹性体,本构关系有21个弹性常数,对于具有一个弹性对称面的各向异性材料,本构各向具有13个弹性常数。
对于正交各向异性材料,弹性常数有9个。
正交各向异性材料的本构方程中,正应力仅与正应变有关,切应力仅与对应的切应变有关,因此拉压与剪切之间,以及不同平面内的剪切之间将不存在耦合作用。
1. 极端各向异性体的弹性常数为21个。
2.具有一个对称面的各向异性材料正交各向异性体:物体内的任一点存在三个弹性对称平面,在每一个对称平两侧对称方向上各自具有相同的弹性性质,这种物体称为正交各向异性体。
正交各向异性体的弹性常数为9个。
3.横观各向同性体若物体内的任一点在平行于某一平面的所各方向都具有相同的弹性性质,而垂直于该面的弹性性质不同,这种正交异性体称为横观各向同性体。





弹性材料本构方程简易推导摘要:弹性力学问题的三大基本方程分别为平衡方程,几何方程,本构方程。
文中主要介绍弹性材料弹性阶段的本构方程简要推导过程。
关键词:本构方程;增量理论;弹性1 前言本构方程描述的是材料应力与应变之间的关系,其具有更广泛的含义,凡是描述介质的应力或应力率、应变或应变率等之间关系的物性方程,统称为本构方程。
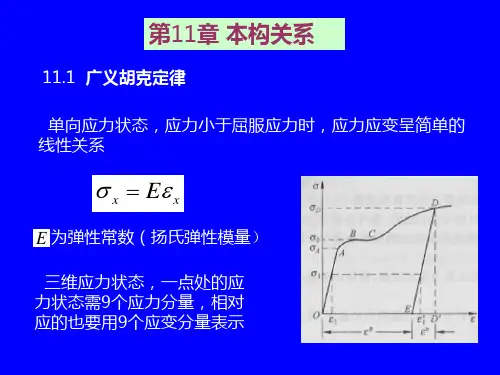
2 弹性阶段本构方程推导2.1 方程建立弹塑性材料处于弹性阶段,即当应力小于屈服应力时,由材料力学相关知识可知应力与应变之间符合Hooke定律:,其中E为弹性常数(杨氏弹性模量)。
三维应力状态下,材料内部一点处应力状态有9个应力分量,故对应于9个应变分量。
由应力张量与应变张量的对称性,,独立的应力分量与应变分量各为6个。
对于均匀的理想弹性体,假设应力应变关系式可表达如下:(1)其中(m, n=1, 2,3, 4, 5,6)为弹性系数,由材料性质决定,与坐标x, y, z无关。
2.2 系数确定2.2.1各向同性材料本构方程对于各向同性材料,独立的弹性常数只有两个,故在最终得出的本构方程中仅使用两个系数来表示应力应变关系。
在弹性状态下主应力方向即为主应变方向。
令坐标轴Ox, Oy, Oz与主应力方向相一致,此时,各应力面无剪应力,只有正应力,故式(1)变化如下:(2)各向同性材料中,对的影响与对及对的影响相同,即有。
同理,和对的影响相同,即,类似有:,等,因而令(3)于是,对于应变主轴(用1, 2, 3代替x, y, z)来说,弹性常数有两个这里设为P和Q。
将式(3)带入式(2),并令,,(此过程作者水平有限,目前尚不能完整导出,直接借助结论)可得出下列弹性本构关系:(4)其中,常数称为拉梅弹性常数,在此可以看出主轴坐标系下,本构方程只含两个未知参数。
于是,在任意坐标系中弹性阶段本构方程为:(5)利用求和约定,式(5)可改写成(5´)以上为各向同性材料在弹性阶段本构方程,但在此,方程中λ,μ两参数仍不能直接得出,不能在后期工程计算应用中方便使用。