消费函数模型

柯布-道格拉斯效用函数（Cobb-Douglas Utility Function）是一种常用的经济学中描述消费者效用函数的数学模型。

它用于表示消费者对不同商品的效用或满足程度。

柯布-道格拉斯效用函数的一般形式为：
U = A * X^a * Y^b
其中，U 表示效用，A 是常数，X 和Y 是两种商品的数量，a 和 b 是表示商品对效用的弹性或重要程度的参数。

柯布-道格拉斯效用函数具有以下特点：
多样性效应：当a 和b 的值大于0 时，增加某种商品的数量会增加效用，即多样性效应。

消费者越多样化地消费两种商品，效用越高。

边际效用递减：随着某种商品的数量增加，其边际效用递减，即每多消费一单位的商品，效用的增加幅度越来越小。

均衡性：在消费者选择最优消费组合时，边际效用与价格之比（边际替代率）应相等，以达到效用最大化。

柯布-道格拉斯效用函数在经济学中被广泛应用于描述消费者的偏好和选择行为，以及衡量经济中的效用和福利。

在实际分析中，参数a 和 b 的具体数值会根据具体情境和数据进行估计。

经济学里面的数学方程经济学中常使用的数学方程和模型多种多样，它们帮助经济学家分析和预测经济现象。

以下是一些常见的经济学数学方程和模型：1.供需方程：o供给函数：Qs = f(Ps)o需求函数：Qd = g(Pd)当Qs = Qd时，市场达到均衡，此时的价格称为均衡价格，对应的数量称为均衡数量。

2.市场均衡模型：o P = MC = MR = AR其中，P是价格，MC是边际成本，MR是边际收益，AR是平均收益。

当边际成本等于边际收益时，企业实现利润最大化。

3.消费者行为模型：o效用函数：U = u(x1, x2, ..., xn)描述消费者在给定商品组合下的效用水平。

4.生产函数：o Q = f(K, L)其中，Q是产出，K是资本，L是劳动。

这个函数描述了给定资本和劳动投入下的最大产出。

5.成本函数：o TC = TFC + TVC其中，TC是总成本，TFC是固定成本，TVC是可变成本。

o AC = TC / Q其中，AC是平均成本。

o MC = ∆TC / ∆Q其中，MC是边际成本。

6.无差异曲线：用于描述消费者在不同商品组合之间获得相同效用水平的路径。

7.等产量线：在生产空间中，表示给定生产要素投入组合下能生产出的最大产量。

8.IS-LM模型：o IS曲线：描述产品市场均衡时利率与国民收入之间的关系。

o LM曲线：描述货币市场均衡时利率与国民收入之间的关系。

9.总需求-总供给模型：o AD = C + I + G + (X - M)其中，AD是总需求，C是消费，I是投资，G是政府支出，X是出口，M是进口。

o AS = Y其中，AS是总供给，Y是国民收入。

10.菲利普斯曲线：oπ = πe - β(u - un)其中，π是实际通货膨胀率，πe是预期通货膨胀率，u是实际失业率，un是自然失业率，β是调整系数。

这些方程和模型在经济学中被广泛应用，用于分析市场行为、消费者选择、生产决策、宏观经济政策等各个方面。

03 第三节常用经济函数常用经济函数是经济学中用来描述经济变量之间关系的数学模型。

这些函数可以用来分析经济发展、预测经济趋势、制定经济政策等。

下面介绍几种常用的经济函数及其含义。

一、消费函数消费函数是指消费者在某一时期内消费的商品或服务的数量与收入之间的函数关系。

通常表示为C=f(Y)，其中C表示消费，Y表示收入。

消费函数曲线是一条向右上方倾斜的曲线，表示随着收入的增加，消费也会增加。

但在达到一定收入后，消费增长速度会逐渐减缓，甚至出现零增长或负增长。

二、投资函数投资函数是指企业在某一时期内进行的投资数量与资本存量之间的函数关系。

通常表示为I=f(K)，其中I表示投资，K表示资本存量。

投资函数曲线是一条向右上方倾斜的曲线，表示随着资本存量的增加，投资也会增加。

但在达到一定资本存量后，投资增长速度会逐渐减缓，甚至出现零增长或负增长。

三、总供给函数总供给函数是指某一时期内，企业愿意且有能力提供的商品和服务的总量与价格水平之间的函数关系。

通常表示为Y=f(P)，其中Y表示总供给，P表示价格水平。

总供给函数曲线是一条向右下方倾斜的曲线，表示随着价格水平的提高，总供给会减少。

但在达到一定价格水平后，总供给增长速度会逐渐减缓，甚至出现零增长或负增长。

四、总需求函数总需求函数是指某一时期内，消费者愿意且有能力购买的商品和服务的总量与价格水平之间的函数关系。

通常表示为Y=f(P)，其中Y表示总需求，P表示价格水平。

总需求函数曲线是一条向右下方倾斜的曲线，表示随着价格水平的提高，总需求会减少。

但在达到一定价格水平后，总需求增长速度会逐渐减缓，甚至出现零增长或负增长。

五、菲利普斯曲线菲利普斯曲线是指通货膨胀率与失业率之间的函数关系。

通常表示为π=f(u)，其中π表示通货膨胀率，u表示失业率。

菲利普斯曲线是一条向右下方倾斜的曲线，表示随着失业率的降低，通货膨胀率会上升。

但在达到一定失业率后，通货膨胀率增长速度会逐渐减缓，甚至出现零增长或负增长。

凯恩斯的绝对收入假说(重定向自绝对收入理论)绝对收入假说(Absolute Income Hypothesis，简称AIH）——也称为绝对收入理论、绝对收入假设、绝对收入假设消费函数模型凯恩斯的绝对收入假说概述凯恩斯的绝对收入假说，认为，在短期中，收入与消费是相关的，即消费取决于收入，消费与收入之间的关系也就是消费倾向。

同时，随着收入的增加消费也将增加，但消费的增长低于收入的增长，消费增量在收入增量中所占的比重是递减的，也就是我们所说的边际消费倾向递减，这种理论被称为绝对收入假说。

绝对收入假说：收入的绝对水平决定消费（约翰·梅纳德·凯恩斯John Maynard Keynes）相对收入假说：收入的分配状况及消费者历史上最高的收入水平决定消费（詹姆斯·杜森贝里James Stemble Duesenberry）生命周期假说：消费者根据一生的收入流来优化一生的消费流（弗兰科·莫迪利安尼Franco Modigliani）持久收入假说：持久性（而非暂时性）收入水平决定消费（米尔顿·弗里德曼Milton Friedman）凯恩斯的绝对收入假说的公式凯恩斯的绝对收入假说是假定消费是人们收入水平的函数,其基本公式是:C= α + βYt(式中C为现期消费,α为自发性消费即必须要有的基本生活消费,β为边际消费倾向,Yt为即期收入,βYt表示引致消费),它的基本含义是消费是自发消费和引致消费的和,消费者的消费主要取决于即期收入。

凯恩斯的绝对收入假说的主要观点凯恩斯的绝对收入假说的其主要观点如下：第一，实际消费支出是实际收入的稳定函数。

第二，收入是指现期绝对实际收入水平。

第三，边际消费倾向是正值，但小于1。

第四，边际消费倾向随收入增加而递减。

第五，边际消费倾向小于平均消费倾向。

概括起来，绝对收入假说的中心是消费取决于绝对收入水平，以及边际消费的倾向递减。

相对收入假说(重定向自相对收入理论)相对收入假说（relative income hypothesis，简称RIH）也称杜森贝里的短期消费函数、“不可逆性”假设消费函数模型、相对收入假设什么是相对收入假说相对收入假说是1949年美国经济学家詹姆斯·杜森贝里(James Stemble Duesenberry)在《收入、储蓄和消费者行为理论》中提出来的。

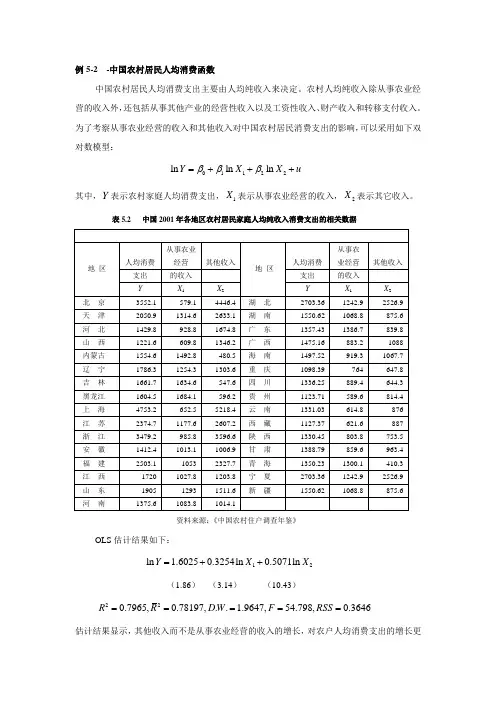
例5-2 -中国农村居民人均消费函数中国农村居民人均消费支出主要由人均纯收入来决定。

农村人均纯收入除从事农业经营的收入外，还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入。

为了考察从事农业经营的收入和其他收入对中国农村居民消费支出的影响，可以采用如下双对数模型：01122ln ln ln Y X X u βββ=+++其中，Y 表示农村家庭人均消费支出，1X 表示从事农业经营的收入，2X 表示其它收入。

表5.2 中国2001年各地区农村居民家庭人均纯收入消费支出的相关数据资料来源：《中国农村住户调查年鉴》OLS 估计结果如下：12ln 1.60250.3254ln 0.5071ln Y X X =++（1.86） （3.14） （10.43）220.7965,0.78197,.. 1.9647,54.798,0.3646R R DW F RSS =====估计结果显示，其他收入而不是从事农业经营的收入的增长，对农户人均消费支出的增长更有刺激作用。

下面对该模型进行异方差性检验。

可以认为不同地区农村人均消费支出的差别主要来源于非农经营收入及其他收入的差别，因此，如果存在异方差性，则可能是其他收入2X 引起的。

模型OLS 回归得到的残差平方项2~i e 与2ln X 的散点图表明，存在单调递增型异方差性。

再进一步的G-Q 检验和White 检验，均发现存在异方差性。

G-Q 检验和White 检验的具体方法参考案例1，我们这里主要介绍异方差稳健标准误法。

使用Eviews ，先点击Quick, 选择Estimate Equation ，再点击Options ，选择White ，即可得到诸方差的怀特异方差性一致估计量值以及对应的稳健t 统计值。

估计方程如下：12ln 1.60250.3254ln 0.5071ln Y X X =++（2.23） （3.05） （7.81）220.7965,0.78197,.. 1.9647,54.798,0.3646R R DW F RSS =====.。

常用经济函数模型经济函数模型是用来描述经济变量之间关系的数学模型。

在经济学中，一些常用的经济函数模型包括：1.消费函数模型：描述消费支出与收入之间的关系。

一般形式为C=α+βY，其中C表示消费支出，Y表示收入，α和β是参数。

这个模型表明消费支出与收入之间存在正相关关系，即收入越高，消费支出也越高。

2.投资函数模型：描述投资支出与利率之间的关系。

一般形式为I=I0(r)，其中I表示投资支出，r表示利率，I0是利率为零时的投资支出。

这个模型表明投资支出与利率之间存在负相关关系，即利率越高，投资支出越少。

3.生产函数模型：描述一定时期内生产过程中各要素的投入与产出之间的关系。

一般形式为Y=F(X1,X2,Xn)，其中Y表示总产出，X1,X2,Xn表示各种生产要素的投入量，F是生产函数。

这个模型表明在一定时期内，生产要素的投入量与产出量之间存在一定的函数关系。

4.成本函数模型：描述一定时期内生产成本与产量之间的关系。

一般形式为C=C(Y)，其中C表示总成本，Y表示总产量。

这个模型表明在一定时期内，随着产量的变化，生产成本也会发生变化。

5.收益函数模型：描述一定时期内销售收入与销售量之间的关系。

一般形式为R=R(Q)，其中R表示总收入，Q表示销售量。

这个模型表明在一定时期内，随着销售量的变化，销售收入也会发生变化。

6.利润函数模型：描述一定时期内企业利润与产量之间的关系。

一般形式为π=π(Y)，其中π表示总利润，Y表示总产量。

这个模型表明在一定时期内，随着产量的变化，企业利润也会发生变化。

这些经济函数模型在经济学的各个领域中都有广泛的应用。

例如，在宏观经济分析中，可以通过消费函数模型和投资函数模型来预测经济增长；在微观经济分析中，可以通过生产函数模型和成本函数模型来制定企业生产计划和进行成本控制；在市场营销中，可以通过收益函数模型和利润函数模型来制定销售策略和进行利润管理。

需要注意的是，这些经济函数模型都只是对现实经济现象的近似描述，并不完全准确。

“消费函数”的名词解释
“消费函数”是一个经济学术语，指的是描述消费行为与消费支出之间关系的数学函数。

它用于描述个体或家庭在特定时间段内根据其收入和其他因素来做出消费决策的模型。

消费函数通常表示为C = f(Y)，其中C代表消费支出，Y代表可支配收入。

该函数表达了消费支出与可支配收入之间的关系，即人们在不同收入水平下消费的金额。

消费函数可以是线性的、非线性的或其他形式的函数。

线性消费函数表示消费支出与可支配收入成正比。

非线性消费函数则表示消费支出与可支配收入之间存在非线性的关系，可能包括边际消费倾向递减等经济现象。

消费函数的研究对于经济学和个人理财都具有重要意义。

它可以帮助经济学家分析消费者行为、预测经济发展趋势、评估政策效果等。

对个人而言，了解自己的消费函数可以帮助做出理性的消费决策、规划个人预算和财务管理。

需要注意的是，消费函数是一个理论模型，对个体和整体的消费行为进行概括和描述，并不代表每个人的具体消费行为。

实际的消费行为可能受到个人偏好、文化背景、收入分配等多种因素的影响。

消费函数名词解释消费函数是指描述消费与收入之间关系的经济学模型。

它是一种数学方程，用来描述人们在不同收入水平下消费的决策行为。

消费函数的一般形式为C = f(Y)，其中C表示消费，Y表示收入，f(Y)表示消费的函数关系。

消费函数的解释包含以下几个方面：1. 消费倾向：消费函数中的斜率称为消费倾向（MPC，Margin Propensity to Consume）。

它表示了每增加一个单位的收入，消费增加的幅度。

如果消费倾向是0.7，意味着每增加1单位的收入，消费增加0.7单位。

消费倾向是消费函数的重要参数，它反映了人们对收入变动的敏感程度。

2. 储蓄倾向：储蓄倾向（MPS，Margin Propensity to Save）是指每增加1单位的收入，储蓄增加的幅度。

储蓄倾向等于1减去消费倾向。

如果消费倾向是0.7，那么储蓄倾向就是0.3。

储蓄倾向是消费函数的补充参数，它与消费倾向形成互补关系。

3. 边际消费倾向：边际消费倾向（MPC）是指每增加1单位的收入，消费增加的额外值。

它是消费倾向的导数，表示了消费对收入变动的敏感程度的变化率。

边际消费倾向越大，表明消费对收入变动的敏感程度越高。

4. 自由消费：自由消费是指在一定收入水平下，人们的消费行为。

它等于收入减去储蓄。

自由消费与收入成正相关，即收入增加，自由消费也会增加。

5. 基本消费：基本消费是指在零收入的情况下，人们的最低生活消费。

它是消费函数中的截距项（c）。

消费函数的解释还可以进一步包括消费的自我调整机制和影响消费的其他因素。

消费函数是一种理论模型，用来描述和解释人们对收入变动的消费行为，对于经济学家和政策制定者来说具有重要的参考意义。

通过研究消费函数，可以了解收入变动对消费的影响，为经济政策的制定和调整提供依据。

消费函数理论弗里德曼消费函数理论是经济学家弗里德曼（Milton Friedman）提出的一种描述消费与收入之间关系的理论模型。

根据这个理论，个人的消费行为取决于其可支配收入水平，而不仅仅是当前的收入水平。

消费函数的基本形式是C = a + bYd，其中C代表个人的消费水平，a代表基本消费水平，b代表消费的边际倾向（即可支配收入的一部分被用于消费的比例），Yd代表个人的可支配收入。

消费函数的形式可以用来解释个人在面对不同收入水平时的消费决策。

根据消费函数理论，个人的消费水平取决于其可支配收入水平，因此随着收入的增加，个人的消费也会相应地增加。

然而，消费的边际倾向通常小于1，这意味着每增加一单位的可支配收入，个人的消费只增加不到一单位。

这部分可支配收入的不消费部分被称为储蓄。

弗里德曼提出的消费函数理论还分析了收入对消费的长期和短期影响。

在短期内，个人更倾向于将更多的可支配收入用于消费，因为他们对未来收入的预期较为不确定。

然而，在长期内，个人更倾向于将更多的可支配收入储蓄起来，以便应对可能出现的不确定性和风险。

消费函数理论还提出了一些其他影响消费决策的因素。

其中一个是富人消费更加倾向于收入风险的可替代消费品，而不是基本的日常消费品。

另一个因素是存在着一种所谓的代际效应，即父母的消费行为会影响到子女的消费决策，这进一步影响了整个经济体系中的消费水平。

然而，消费函数理论也存在一些局限性。

首先，该理论基于个人的收入水平，没有考虑其他因素对消费决策的影响。

例如，人们的消费偏好、信心水平、财富分布等因素也会对消费产生影响。

其次，消费函数理论假设个人在面临不确定性时会倾向于储蓄，但实际情况可能存在个体差异和不确定性的变化。

总之，消费函数理论是经济学家弗里德曼提出的一种描述个人消费与收入之间关系的理论模型。

通过分析个人的消费决策，这一理论为我们了解消费行为提供了基本框架，并对经济政策制定者制定合理政策提供了指导。

消费函数一.含义消费函数是指消费支出与决定消费的各种因素之间的依存关系。

决定消费水平的因素很多，如收入、财产、利率、收入分布等。

其中收入是最根本的因素。

二．消费函数模型演变过程及分析1.消费函数这一概念最先由英国经济学家J.M.凯恩斯提出。

他在《就业、利息和货币通论》（1936）一书中提出：总消费是总收入的函数。

这一思想用线性函数形式表示为：凯恩斯消费函数将消费分为“自发消费”和“引致消费”。

自发消费（a）——是指不受收入影响以及本能消费需要所形成的消费。

引致消费（）——就是指受收入因素和边际消费倾向影响所形成的消费。

它等于：。

设：b为边际消费倾向，Y为收入。

总消费=自发消费+引致消费即Ct=a+bYt,式中C表示总消费,Y表示总收入，下标t表示时期；a、b为参数。

a＞0表示短期内无论个人有无收入都要消费；参数b称为边际消费倾向，其值介于0与1之间，0＜dCt／dYt＝b＜1，d2Ct／dY2t＜0，即：边际消费倾向是小于1的正数，且递减。

平均消费倾向（APC）是消费占收入的比重，公式为：APC＝Ct／Yt＝a／Yt＋b，由于a＞0，Yt＞0，显然，b＜APC＝Ct／Yt＝a／Yt＋b即：边际消费倾向小于平均消费倾向。

2.二战后：式中C t表示t期消费,Y t表示t期收入,C t-1表示上期（t-1期）消费；α，β，γ为参数。

这一消费函数的最后一项可以解释为消费的惯性影响，也可以解释为持久收入的影响。

3.经上式递推推导出：此式表明，消费是过去历年收入的函数。

4.短期消费函数：C t = b+ b1Yt+ b2C（t–1） + μt t=1,2,......,T其中，C t− 1为第t-1期的消费支出。

5.持久收入假说：函数形式为：Ct＝cPYt（1）Ct为现期消费，PYt为现期持久收入，c为现期持久收入的边际消费倾向。

持久收入是持久收入假说的核心，弗里德曼认为，一定时期的持久收入是在过去的持久收入基础上形成的，现期的实际收入的变化也影响持久收入。

十大著名经济学模型经济学模型是描述经济现象和解释经济运行的工具，是经济学理论的抽象呈现和实践应用。

以下是十大著名经济学模型。

1. 简单生产模型简单生产模型是经济学模型中最基础、最简单的模型。

它假设只有一种产品、一个生产部门和一个消费部门，通过生产和消费确定价格和数量。

这个模型是其他复杂模型的基础，可以用于研究一些基本的经济问题。

2. 消费函数模型消费函数模型是研究消费行为的模型。

它通过描述人们的收入、价格水平和偏好等因素，来揭示人们的消费习惯和消费水平。

3. 生产函数模型生产函数模型是描述企业生产过程的模型。

它通过分析企业的生产要素、技术和产出，来确定企业生产的最优组合和产出水平。

4. 供求模型供求模型是研究市场供求关系的模型。

它通过描述买卖双方的行为、市场价格和数量，来揭示市场的均衡价格和数量。

5. IS-LM模型IS-LM模型是描述宏观经济运行的模型。

它通过分析国家总需求和总供给，来揭示宏观经济的均衡水平和波动。

6. 货币数量论模型货币数量论模型是描述货币供应和价格关系的模型。

它通过分析货币供应量和价格水平，来揭示货币政策对价格的影响。

7. Solow增长模型Solow增长模型是描述经济增长的模型。

它通过分析生产要素的增长和技术进步，来揭示经济增长的源泉和限制。

8. 先进技术模型先进技术模型是描述技术进步对经济影响的模型。

它通过分析技术进步对企业生产要素和产出的影响，来揭示技术进步对经济的驱动力和变革。

9. 实物积累模型实物积累模型是描述经济发展的模型。

它通过分析投资和资本积累对经济发展的影响，来揭示经济发展的机制和趋势。

10. 新古典主义增长模型新古典主义增长模型是描述经济增长和技术进步的模型。

它通过分析生产要素的增长和技术进步，来揭示经济增长的源泉和限制。

相对于Solow增长模型，新古典主义增长模型更加动态，能够更好地解释经济的发展和变革。

凯恩斯消费函数理论概述凯恩斯消费函数是由英国经济学家约翰·梅纳德·凯恩斯提出的一种经济理论，用于描述个人消费行为与收入水平之间的关系。

该理论被广泛应用于宏观经济学和经济政策制定中，对于理解和预测经济活动具有重要的意义。

1. 凯恩斯消费函数的基本原理凯恩斯消费函数表达了个人消费支出与可支配收入之间的关系。

根据凯恩斯的理论，个人消费受到多种因素的影响，包括收入、利率、预期和财富等。

在简化的模型中，凯恩斯将消费与可支配收入的关系表示为一个简单的线性函数。

2. 凯恩斯消费函数的数学表达式凯恩斯消费函数可以用如下数学表达式表示：C = a + bYd其中，C表示消费支出，a表示基本消费支出，b表示消费与可支配收入之间的关系比例，Yd表示可支配收入。

该函数表达了消费支出与可支配收入之间的线性关系，即消费随着可支配收入的增加而增加。

3. 凯恩斯消费函数的理论解释凯恩斯消费函数的理论解释可以分为两个方面：边际倾向消费倾向和绝对收入假说。

3.1 边际倾向消费倾向凯恩斯认为，个人消费不仅依赖于可支配收入的绝对水平，还与可支配收入的变动相关。

边际倾向消费倾向（Marginal Propensity to Consume, MPC）表示每个单位可支配收入变动引起的消费变动。

凯恩斯假设MPC是一个介于0和1之间的数值，即随着收入的增加，人们倾向于消费更多的收入。

3.2 绝对收入假说凯恩斯的另一个理论假设是绝对收入假说。

他认为，人们的消费水平主要取决于他们的绝对收入水平，而不仅仅是相对于其他人的收入水平。

这意味着无论收入分配如何，人们的消费行为都与他们的绝对收入密切相关。

4. 凯恩斯消费函数的政策意义凯恩斯消费函数的研究不仅拓宽了我们对消费行为的理解，还对经济政策的制定具有指导意义。

政府可以通过调整相关因素来影响个人消费行为，从而促进经济增长和稳定。

4.1 政府支出的影响凯恩斯提出了“乘数效应”的概念，即政府支出的增加将带动更多的消费支出。

消费函数公式消费函数是经济学中常用的模型之一，用于描述人们在不同收入水平下的消费行为。

它是通过分析收入与消费之间的关系来揭示消费者行为的规律和特征的。

消费函数的一般形式可以表示为C = f(Y)，其中C表示消费支出，Y表示收入。

这个函数表明消费支出是收入的函数，即收入的变化会影响消费支出的变化。

消费函数可以通过经济数据的分析和统计方法来估计和推导。

消费函数的核心思想是消费者在面对不同收入水平时，会按照一定的规律对其进行分配和支出。

一般来说，随着收入的增加，消费支出也会增加，但增幅逐渐减小。

这是因为当收入较低时，消费者的基本需求是首要考虑的，因此他们会将大部分收入用于满足基本生活需求，如食物、住房和教育等。

随着收入的增加，消费者的基本需求逐渐得到满足，他们会开始考虑一些非基本需求，如旅游、娱乐等消费。

但随着收入的继续增加，消费者的边际消费倾向逐渐下降，也就是说，他们对额外收入的消费倾向会减弱。

这是因为当收入较高时，消费者已经满足了大部分的需求，所以他们对额外收入的消费欲望会降低。

除了收入之外，消费函数还受到其他因素的影响，如利率、物价水平、金融市场状况等。

例如，当利率较低时，消费者倾向于增加借贷消费，从而增加消费支出；而当利率较高时，消费者倾向于减少借贷消费，从而减少消费支出。

此外，物价水平的变化也会影响消费者的消费决策。

当物价上涨时，消费者的购买力下降，他们可能会减少消费支出；而物价下降时，消费者的购买力增加，他们可能会增加消费支出。

在实际应用中，消费函数对于政府制定经济政策和企业制定市场策略都具有重要意义。

政府可以通过调整税收政策、提高就业水平等手段来增加人们的收入，从而刺激消费支出，促进经济增长。

而企业则可以根据消费函数的特征来制定产品定价和市场推广策略，以满足消费者不同收入水平下的需求。

消费函数作为经济学中的重要模型，可以帮助我们理解消费者行为的规律和特征。

它通过分析收入与消费之间的关系，揭示了消费者在不同收入水平下的消费决策规律。

弗里德曼消费函数理论弗里德曼消费函数理论是经济学中一个重要的概念，也是经济学研究中一个非常普遍的模型。

它主要是用来研究一个家庭或一个个人消费成本和收入水平之间的关系，也可以用来研究其他更多的不同模型，比如储蓄、债务、投资等。

因此，弗里德曼消费函数理论可以成为一个更加全面的经济学模型来研究家庭和个人的消费者行为。

弗里德曼消费函数理论由英国经济学家亨利弗里德曼首创，他在1920年的文章《我们的经济秩序》中提出了这一概念。

该理论认为，家庭的消费水平取决于收入水平，而收入水平又取决于收入源。

因此，家庭或个人消费水平取决于收入水平和收入源之间的关系。

同时，弗里德曼消费函数也可以用来描述一个家庭的消费偏好，以及它们如何在收入水平、收入源及其它影响之间来决定消费水平。

弗里德曼消费函数理论也可以用来研究经济增长，它可以用来说明经济增长的原因。

它认为，经济增长的原因有两个：第一，收入增加，收入源可以是劳动力报酬、资本收益、利息收入等；第二，人们改变了消费习惯，比如更喜欢购买更多的服务和产品，比如新技术产品、旅游服务等。

综上，弗里德曼消费函数理论可以用来研究个人消费、经济增长以及家庭的收支情况，是一个模型的全面概念。

弗里德曼消费函数理论的有效性受到许多经济学家的挑战，特别是在宏观经济学方面。

这是因为宏观经济中的收入来源和消费习惯比微观经济更为复杂，而弗里德曼消费函数理论没有涉及宏观经济学。

另外，弗里德曼消费函数假定为完全市场经济，但不考虑位置性、租金、财富差异等因素，因此也受到了质疑。

尽管弗里德曼消费函数理论受到许多经济学家的质疑，但该理论仍然是经济学研究的基础，在宏观经济学领域中也有广泛的应用。

例如，可以使用弗里德曼消费函数来理解政府对消费者行为的影响，比如财政政策对消费者行为的影响。

另外，也可以使用弗里德曼消费函数来研究宏观经济学中收入分配函数的变化，这也很有用。

综上所述，弗里德曼消费函数理论是一个非常重要的经济学模型，有着重要的实践意义和研究价值，也有着广泛的应用。