中国农村居民消费函数模型分析

实验三异方差性实验目的：在理解异方差性概念和异方差对OLS回归结果影响的基础上,掌握进行异方差检验和处理的方法;熟练掌握和运用Eviews软件的图示检验、G-Q检验、怀特White 检验等异方差检验方法和处理异方差的方法——加权最小二乘法;实验内容：书P116例4.1.4：中国农村居民人均消费函数中国农村居民民人均消费支出主要由人均纯收入来决定;农村人均纯收入除从事农业经营的收入外,还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入等;为了考察从事农业经营的收入和其他收入对中国农村居民消费支出增长的影响,建立双对数模型：其中,Y表示农村家庭人均消费支出,X1表示从事农业经营的纯收入,X2表示其他来源的纯收入;表4.1.1列出了中国内地2006年各地区农村居民家庭人均纯收入及消费支出的相关数据;表4.1.1 中国2006年各地区农村居民家庭人均纯收入与消费支出单位：元注：从事农业经营的纯收入由从事第一产业的经营总收入与从事第一产业的经营支出之差计算,其他来源的纯收入由总纯收入减去从事农业经营的纯收入后得到;资料来源：中国农村住户调查年鉴2007、中国统计年鉴2007;实验步骤：一、创建文件1.建立工作文件CREATE U 1 31 其中的“U”表示非时序数据2.录入与编辑数据Data Y X1 X2 意思是：同时录入Y、X1和X2的数据3.保存文件单击主菜单栏中File→Save或Save as→输入文件名、路径→保存;二、数据分析1.散点图①Scat X1 Y从散点图可看出,农民农业经营的纯收入与农民人均消费支出呈现一定程度的正相关;②Scat X2 Y从散点图可看出,农民其他来源纯收入与农民人均消费支出呈现较高程度的正相关;2.数据取对数处理Genr LY=LOG YGenr LX1=LOG X1Genr LX2=LOG X2三、模型OLS 参数估计与统计检验 LS LY C LX1 LX2得到模型OLS 参数估计和统计检验结果：Dependent Variable: LY Method: Least Squares Sample: 1 31Variable CoefficientStd. Errort-StatisticProb.C LX1 R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihood F-statistic 注意：在学术文献中一般以这种形式给出回归方程的输出结果,而不是把上面的软件输出结果直接粘贴到文章中可决系数,调整可决系数,显示模型拟合程度较高;同时,F 检验统计量,在5%的显着性水平下通过方程总体显着性检验;可认为农民农业经营的收入和其他收入整体与农村居民消费支出的线性关系显着成立;变量X2和截距项均在5%的显着性水平下通过变量显着性检验,但X1在10%的显着水平下仍不能通过检验;四、异方差检验对于双对数模型,由于12(0.150214)(0.477453)ββ=<=二者均为弹性系数,可认为其他来源的纯收入而不是从事农业经营的纯收入的增长,对农户人均消费的增长更有刺激作用;也就是说,不同地区农村人均消费支出的差别主要来源于非农经营收入及工资收入、财产收入等其他来源收入的差别,因此,如果模型存在异方差性,则可能是X2引起的;1.图示检验法观察残差的平方与LX2的散点图;①残差resid残差resid变量数据是模型参数估计命令完成后由Eviews软件自动生成在Workfile 框里可找到,无需人工操作获得;注意,resid保留的是最近一次估计模型的残差数据;②残差的平方与LX2的散点图Scat LX2 resid^2从上图可大体判断出模型存在递增型异方差性;2．G-Q法检验异方差补充：先定义一个变量T,取值为1、2、…、31分别代表各省市,用于在做完G-Q检验之后,再按T排序,使数据顺序还原;Data T 提示：输入1、2、…、31①将所有原始数据按照X2升序排列;Sort X2Show Y X1 X2 LY LX1 LX2显示各个变量数据的目的是查看一下,所有变量数据是否按X2升序排列好了;②将31对样本数据,去掉中间的7对,形成两个容量均为12的子样本,即1-12和20-31;③对1-12的子样本做普通最小二乘估计,并记录残差平方和RSS;1Smpl 1 12 意思是：将样本区间由1-31,改为1-12Ls LY C LX1 LX2Dependent Variable: LYMethod: Least Squares Sample: 1 12C LX1 LX2R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihood F-statistic Durbin-Watson statProbF-statistic子样本1：12ln 3.1412080.398385ln 0.234751ln Y X X e =+++1RSS =④对20-31的子样本做普通最小二乘估计,并记录残差平方和2RSS ; Smpl 20 31 意思是：将样本区间由1-12,改为20-31 Ls LY C LX1 LX2Dependent Variable: LY Method: Least Squares Sample: 20 31Included observations: 12C LX1 R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihood F-statistic Durbin-Watson statProbF-statistic子样本2：12ln 3.9936440.113766ln 0.6201681ln Y X X e =-++2RSS =⑤异方差检验在5%与10%的显着性水平下,自由度为9,9的F分布临界值分别为0.05(9,9) 3.18F=与0.10(9,9) 2.44F=;因此5%显着性水平下不能拒绝同方差假设,但在10%的显着性水平下拒绝;补充：怀特检验软件操作：在原始模型的OLS方程对象窗口中,选择view/Residual test/White Heteroskedasticity;Eviews提供了包含交叉项的怀特检验“White Heteroskedasticitycross terms”和没有交叉项的怀特检验“White Heteroskedasticityno cross terms”这样两个选择;问题：如果是刚做完上面的G-Q检验,如何得到原始模型答案：先恢复成全样本,再按T排序,然后做OLS回归;SMPL 1 31 意思是：将样本区间恢复到1-31补充：将样本数据按T升序排列,使数据顺序还原;Sort T 意思是：将数据顺序还原Ls LY C LX1 LX2下面是在原始模型的OLS方程对象窗口中,选择view/Residual test/White Heteroskedasticity,然后进行包含交叉项的怀特检验“White Heteroskedasticitycross terms”所得到的输出结果最上方显示了两个检验统计量：F统计量和White统计量nR2；下方显示的是以OLS的残差平方为被解释变量的辅助回归方程的回归结果：F-statistic ProbabilityTest Equation:Dependent Variable: RESID^2Method: Least SquaresDate: 05/03/11 Time: 17:21Sample: 1 31C LNX1 LNX1^2 LNX1LNX2 LNX2 R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihood F-statistic 可见,怀特统计量nR 2==31×,大于自由度也即辅助回归方程中解释变量的个数为5的2分布临界值07.115205.0=）（χ,因此,在5%的显着性水平下拒绝同方差的原假设; 五、采用加权最小二乘法处理异方差以下内容和教材P118-120不一样,但是我们必须掌握的重点——以原始模型的OLS 回归残差的绝对值的倒数为权数,手工完成加权最小二乘估计LS LY C LX1 LX2Genr E=resid 意思是：记录双对数模型OLS 估计的残差 用残差的绝对值的倒数对LY 、LX1、LX2做加权： Genr LYE=LY/abs E Genr LX1E=LX1/abs E Genr LX2E=LX2/abs E Genr CE=1/abs E LS LYE CE LX1E LX2EDependent Variable: LYE Method: Least Squares Sample: 1 31CELX1ER-squared Mean dependent varAdjusted R-squared . dependent var. of regression Akaike info criterionSum squared resid Schwarz criterionLog likelihood Durbin-Watson stat可以看出,lnX1参数的t统计量有了显着改进,这表明在1%显着性水平下,都不能拒绝从事农业生产带来的纯收入对农户人均消费支出有着显着影响的假设;六、检验加权的回归模型是否还存在异方差1.检验是否由LX1E引起异方差Sort LX1E 意思是：将原始数据按LX1E升序排列①子样本1的回归：Smpl 1 12LS LYE CE LX1E LX2EDependent Variable: LYEMethod: Least SquaresSample: 1 12Variable Coefficient Std. Error t-Statistic Prob.CELX1ER-squared Mean dependent varAdjusted R-squared . dependent var. of regression Akaike info criterionSum squared resid Schwarz criterionLog likelihood Durbin-Watson stat子样本1：RSS=1②子样本2的回归：Smpl 20 31LS LYE CE LX1E LX2EDependent Variable: LYE Method: Least Squares Date: 05/01/11 Time: 23:23 Sample: 20 31Variable CoefficientStd. Errort-StatisticProb.CE LX1E R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihoodDurbin-Watson stat子样本2：2RSS =③异方差检验 注意做题的步骤提出假设 22012:H σσ= 22112:H σσ≠ 计算检验统计量：在5%的显着性水平下,自由度为9,9的F 分布临界值分别为0.05(9,9) 3.18F =;因此5%显着性水平下不能拒绝同方差假设;2.检验是否由LX2E 引起异方差Smpl 1 31 意思是：将样本区间复原Sort lx2e 意思是：将原始数据按LX2E 升序排列 ①子样本1的回归： Smpl 1 12LS LYE CE LX1E LX2EDependent Variable: LYE Method: Least Squares Sample: 1 12CE LX1E R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihoodDurbin-Watson stat子样本1：1RSS = ②子样本2的回归： Smpl 20 31LS LYE CE LX1E LX2EDependent Variable: LYE Method: Least Squares Sample: 20 31Included observations: 12CE LX1E R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared resid Schwarz criterion Log likelihoodDurbin-Watson stat子样本2：2RSS =③异方差检验 注意做题的步骤提出假设 22012:H σσ= 22112:H σσ≠ 计算检验统计量：在5%的显着性水平下,自由度为9,9的F 分布临界值分别为0.05(9,9) 3.18F =;因此5%显着性水平下不能拒绝同方差假设;结论：用OLS 估计的残差绝对值的倒数作为权数,对存在异方差的模型加权,然后采用OLS估计,则一定会消除异方差;最终通过异方差检验的估计方程为：实验四序列相关性实验目的：在理解序列相关性的基本概念、序列相关的严重后果的基础上,掌握进行序列相关检验和处理的方法;熟练掌握Eviews软件的图示检验、DW检验、拉格朗日乘数LM检验等序列相关性检验方法和处理序列相关性的方法——广义差分法;实验内容：书P132例4.2.1：中国居民总量消费函数建立总量消费函数是进行宏观经济管理的重要手段;为了从总体上考察中国居民收入与消费的关系,P56表2.6.3给出了中国名义支出法国内生产总值GDP、名义居民总消费CONS以及表示宏观税负的税收总额TAX、表示价格变化的居民消费价格指数CPI1990=100,并由这些数据整理出实际支出法国内生产总值GDPC=GDP/CPI、居民实际消费总支出Y=CONS/CPI,以及实际可支配收入X=GDP-TAX/CPI;表2.6.3 中国居民总量消费支出与收入资料单位：亿元年份GDP CONS CPI TAX GDPC X Y19781979198019811982198319841985198619871988198919901991199219931994199519961997199819992000200120022003200420052006资料来源：根据中国统计年鉴2001,2007整理;实验步骤：一、创建文件1.建立工作文件CREATE A 1978 2006 其中的“A”表示年度数据2.录入与编辑数据Data X Y3.保存文件单击主菜单栏中File→Save或Save as→输入文件名、路径→保存;二、数据分析:趋势图Plot X Y 意思是：同时画出Y和X的趋势图从X和Y的趋势图中可看出它们存在共同变动趋势;三、OLS参数估计与统计检验LS Y C XDependent Variable: YMethod: Least Squares Sample: 1978 2006C R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterion Sum squared residSchwarz criterion Log likelihood F-statistic Durbin-Watson statProbF-statistic从OLS 估计的结果看,模型拟合较好：可决系数20.9880R =,截距项和斜率项的t 检验值均大于5%显着性水平下自由度为n-2=27的临界值0.025(27) 2.05t =;而且,斜率项符合经济理论中边际消费倾向在0与1之间的绝对收入假说;斜率项表明,在1978—2006年间,以1990年价计算的中国居民可支配总收入每增加1亿元,居民消费支出平均增加亿元;四、序列相关性检验 1.图示检验法①残差与时间t 的关系图趋势图 Plot resid②相邻两期残差之间的关系图 Scat resid-1 resid从两个关系图看出,随机误差项呈正序列相关性;.检验值为,表明在5%显着性水平下,n=29,k=2包括常数项,查表得1.34L d =, 1.48U d =,由于.= 1.34L d <=,故存在正序列相关;五、处理序列相关1.修正模型设定偏误剔除虚假序列相关首先面临的问题是,模型的序列相关是纯序列相关,还是由于模型设定有偏误而导致的虚假序列相关;从X 和Y 的趋势图中看到它们表现出共同的变动趋势,因此有理由怀疑较高的2R =部分地是由这一共同的变化趋势带来的;为了排除时间序列模型中这种随时间变动而具有的共同变化趋势的影响,一种解决方案是在模型中引入时间趋势项,将这种影响分离出来;由于本例中可支配收入X 与消费支出Y 均呈非线性变化态势,因此引入的时间变量TT=1,2,……,29以平方的形式出现,回归模型变化为：①编辑变量T data T在数据表中输入1-29; ②做如下的回归 Ls Y C X T^2Dependent Variable: Y Method: Least Squares Sample: 1978 2006 Included observations: 29C X T ^2R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid 6054792. Schwarz criterionLog likelihood F-statistic 得到如下的修正模型：可见,T 2的t 统计量显着;但是,修正的模型.值仍然较低,没有通过5%显着性水平下的.检验n=29,k=3时,27.1=L D ,56.1=U D ,因此该模型仍存在正序列相关性;补充：序列相关性的拉格朗日乘数检验LM检验在EViews软件中,如果在上面的OLS回归方程界面直接做残差序列的LM检验,那么得到的是如下结果,和书上P133结果不一致：原因：EViews在做LM检验时,为了不损失样本,把滞后残差序列的“前样本”缺失值设定为0Presample missing value lagged residuals set to zero.;这样,它的样本容量仍然是n,而不是n-p;回归结果和书上也有不同;解决办法：要使软件的LM检验结果和教材P133结果一致,办法是进行OLS估计之后,先把残差序列resid用genr生成另一序列e,再做辅助回归,即：genr e=resid先做含1阶滞后残差的辅助回归：ls e c x t^2 e-1Dependent Variable: EMethod: Least SquaresDate: 04/26/13 Time: 07:08Sample adjusted: 1979 2006Included observations: 28 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.CXT^2E-1R-squared Mean dependent varAdjusted R-squared . dependent var. of regression Akaike info criterionSum squared resid 2103016. Schwarz criterionLog likelihood Hannan-Quinn criter.F-statistic Durbin-Watson statProbF-statisticLM检验统计量必须自己算：LM=n-pR2=29-1=由于该值大于显着性水平为5%、自由度为1的2分布临界值84.31205.0=）（χ,由此判断原模型存在1阶序列相关;再做含2阶滞后残差的辅助回归： ls e c x t^2 e-1 e-2Dependent Variable: E Method: Least Squares Date: 04/26/13 Time: 07:32 Sample adjusted: 1980 2006Included observations: 27 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob. C X T^2 E-1 E-2R-squaredMean dependent var Adjusted R-squared . dependent var . of regressionAkaike info criterion Sum squared resid 1806465. Schwarz criterion Log likelihood Hannan-Quinn criter. F-statistic Durbin-Watson statProbF-statisticLM 检验统计量必须自己算：LM=n-pR 2=29-2=由于该值大于显着性水平为5%、自由度为2的2分布临界值99.52205.0=）（χ,由此判断原模型存在序列相关;但2~-t e 的系数未通过5%的显着性检验,表明在5%的显着性水平下不存在2阶序列相关性;所以,结合前面含1阶、2阶滞后残差的辅助回归结果,可以判断在5%的显着性水平下仅存在1阶序列相关性;2.广义差分法处理序列相关①Ls Y C X T^2 AR1Dependent Variable: Y Method: Least Squares Sampleadjusted: 1979 2006Included observations: 28 after adjusting endpoints Variable CoefficientStd. Errort-StatisticProb.C X T^2 AR1R-squaredMean dependent var Adjusted R-squared . dependent var . of regression Akaike info criterionSum squared resid 2164144. Schwarz criterionLog likelihood F-statistic AR1前的参数值即为随机扰动项的1阶序列相关系数,在5%的显着性水平下显着;.= ,在5%显着性水平下,1.18.. 1.65L U d DWd =<<=样本容量为28,无法判断广义差分变换后模型是否已不存在序列相关;②继续引入AR2以下内容和教材P133-134的做法不同,但是我们必须掌握的基本做法Ls Y C X T ^2 AR1 AR2Dependent Variable: Y Method: Least Squares Sampleadjusted: 1980 2006Included observations: 27 after adjusting endpointsC X T^2 AR1 AR2R-squaredMean dependent var Adjusted R-squared. dependent var. of regression Akaike info criterionSum squared resid 1834086. Schwarz criterionLog likelihood F-statisticInverted AR Roots .53 .53+.32iAR2前的参数在10%的显着性水平下显着不为0；且.= ,接近于2,认为在10%显着性水平下,已不存在序列相关;但是,在5%的显着性水平下,则没必要引入AR2;注意：教材P133用LM检验的结果是,引入AR1 的回归方程在5%的显着性水平下已不存在序列相关性,因而不需要引入AR2;补充：下面是针对引入AR1的回归方程式的LM检验的命令操作和检验结果：首先,采用上面得到的1阶自回归系数1也即AR1的系数,做如下的1阶广义差分变量的OLS回归注：与式等价：Ls y-1 c x-1 t^t-1^2Dependent Variable: Y-1Method: Least SquaresDate: 06/02/13 Time: 11:07Sample adjusted: 1979 2006Included observations: 28 after adjustmentsVariable Coefficient Std. Error t-Statistic Prob.CX-1T^T-1^2R-squared M ean dependent varAdjusted R-squared . dependent var. of regression A kaike info criterionSum squared resid 2164144. S chwarz criterionLog likelihood H annan-Quinn criter.F-statistic D urbin-Watson statProbF-statistic然后,将上述1阶广义差分方程的残差序列resid 记为e ：genr e=resid 最后,做如下的辅助回归：ls e c x-1 t^t-1^2 e-1Dependent Variable: E Method: Least Squares Date: 06/02/13 Time: 11:16 Sample adjusted: 1980 2006Included observations: 27 after adjustmentsVariable CoefficientStd. Errort-StatisticProb.C X-1 T^T-1^2 E-1R-squaredM ean dependent var Adjusted R-squared . dependent var . of regression A kaike info criterionSum squared resid 1965048. S chwarz criterionLog likelihood H annan-Quinn criter. F-statistic D urbin-Watson statProbF-statistic于是,LM 检验统计量：LM=27=;查表,当显着性水平为5%时,自由度为1的2的临界值）（1205.0χ为;上述LM ＜）（1205.0χ,表明模型的随机误差项已不存在序列相关;。

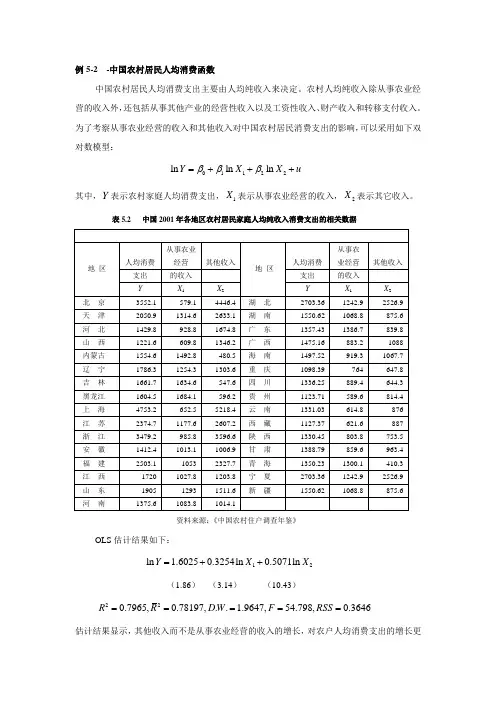
例5-2 -中国农村居民人均消费函数中国农村居民人均消费支出主要由人均纯收入来决定。

农村人均纯收入除从事农业经营的收入外，还包括从事其他产业的经营性收入以及工资性收入、财产收入和转移支付收入。

为了考察从事农业经营的收入和其他收入对中国农村居民消费支出的影响，可以采用如下双对数模型：01122ln ln ln Y X X u βββ=+++其中，Y 表示农村家庭人均消费支出，1X 表示从事农业经营的收入，2X 表示其它收入。

表5.2 中国2001年各地区农村居民家庭人均纯收入消费支出的相关数据资料来源：《中国农村住户调查年鉴》OLS 估计结果如下：12ln 1.60250.3254ln 0.5071ln Y X X =++（1.86） （3.14） （10.43）220.7965,0.78197,.. 1.9647,54.798,0.3646R R DW F RSS =====估计结果显示，其他收入而不是从事农业经营的收入的增长，对农户人均消费支出的增长更有刺激作用。

下面对该模型进行异方差性检验。

可以认为不同地区农村人均消费支出的差别主要来源于非农经营收入及其他收入的差别，因此，如果存在异方差性，则可能是其他收入2X 引起的。

模型OLS 回归得到的残差平方项2~i e 与2ln X 的散点图表明，存在单调递增型异方差性。

再进一步的G-Q 检验和White 检验，均发现存在异方差性。

G-Q 检验和White 检验的具体方法参考案例1，我们这里主要介绍异方差稳健标准误法。

使用Eviews ，先点击Quick, 选择Estimate Equation ，再点击Options ，选择White ，即可得到诸方差的怀特异方差性一致估计量值以及对应的稳健t 统计值。

估计方程如下：12ln 1.60250.3254ln 0.5071ln Y X X =++（2.23） （3.05） （7.81）220.7965,0.78197,.. 1.9647,54.798,0.3646R R DW F RSS =====.。

中国农村居民家庭消费结构分析基于QUAIDS模型的两阶段一致估计一、概述随着中国经济社会的快速发展，农村居民家庭消费结构正在发生深刻的变化。

为了深入探究这一变化背后的规律和特点，本文采用QUAIDS模型进行两阶段一致估计，对中国农村居民家庭消费结构进行了全面细致的分析。

QUAIDS模型（Quadratic Almost Ideal Demand System）作为一种先进的经济学模型，能够基于消费者效用最大化的假设，有效地估计消费者对各类商品的需求响应程度。

我们运用该模型对农村居民家庭的各类消费支出进行了深入研究，包括食品、衣着、耐用品、交通通讯、文化教育、医疗保健等多个方面。

通过对这些消费支出的分析，我们旨在揭示农村居民家庭消费结构的现状、特点及趋势，进而为相关政策制定提供科学依据。

本文还通过对比不同收入水平和地区之间的差异，进一步探讨了消费结构变化的深层次原因。

本文基于QUAIDS模型的两阶段一致估计方法，对中国农村居民家庭消费结构进行了全面而深入的分析，旨在为推动农村经济社会的持续健康发展提供有益的参考和启示。

1. 农村居民家庭消费结构问题的研究背景与意义《中国农村居民家庭消费结构分析基于QUAIDS模型的两阶段一致估计》文章段落生成随着中国经济的快速发展和城乡一体化进程的推进，农村居民家庭消费结构问题逐渐凸显，成为社会各界关注的焦点。

农村居民的收入水平不断提高，消费能力逐渐增强，其消费结构也在发生深刻变化。

与此农村居民家庭消费结构中也存在一些问题，如消费结构单消费层次不高、消费环境不完善等，这些问题不仅制约了农村居民生活质量的提升，也影响了农村经济的可持续发展。

在这样的背景下，对农村居民家庭消费结构进行深入分析，具有重要的理论和现实意义。

消费结构作为反映居民生活水平的重要指标，是衡量农村经济发展状况的重要依据。

通过分析农村居民家庭消费结构，可以深入了解农村居民的消费行为、消费偏好和消费水平，为制定针对性的农村经济发展政策提供科学依据。

中国城镇、农村居民消费的分析与比较消费函数理论不论是在微宏观经济学理论还是在经济统计分析的实践中都具有十分重要的意义。

自从凯恩斯在《通论》中首创绝对收入假说的消费函数理论以来，这一领域就成为经济学家孜孜不倦的研究课题。

在用统计数据检验收入与消费关系的过程中，消费函数不断得到发展和深化，在消费函数理论的发展上前后出现了三个阶段。

第一阶段到第二阶段实现了从短期到长期的飞跃，第二阶段到第三阶段实现了从确定性分析到不确定性分析的跳跃。

第一阶段是以凯恩斯的绝对收入假说和杜森贝里的相对收入假说为代表，主要研究消费支出和现期收入之间的关系，并为两者之间的关系寻求经验数据的支持。

凯恩斯认为消费是现期收入的函数，随着收入的增加消费也增加，但消费增长幅度小于收入增长幅度；而平均消费倾向（消费占收入的比例）随收入的增加而下降，但长期数据却并不支持凯恩斯的这种猜想。

根据杜森贝里的假说，人在消费上存在着“攀比效应”和“棘轮效应”，所以消费除了受当期收入的影响外，还受过去所能达到的最高收入以及他同别人相比的相对收入水平的影响。

阿尔文·费雪的时际选择模型是最早引进不同时期消费者选择的消费函数模型，从而使消费函数理论跨入了第二阶段——跨期消费函数理论阶段。

这一阶段最具有代表性的是生命周期假说和持久收入假说，两者在内容上非常相似。

但前者强调储蓄，后者强调预期收入。

莫迪利安尼认为，消费者会把他一身的资源，包括初始财富W、和一生中赚到的收入分摊到T年生命中，并且希望在一生中实现最平稳的可能的消费路径，在长期中，财富和收入同期增长，所以APC不变，这样就解开了库兹涅茨之谜。

弗里德曼认为，消费不是取决于现期收入，也不取决于最高收入和现期收入的关系，而是取决于持久收入（人们预期持续到未来的那一部分收入）。

第三阶段是对LC-PIH模型的扩充和修正阶段，其代表是霍尔的随机游走假说和预防性储蓄理论。

1978年霍尔将理性预期引入了消费函数，其推理如下：根据持久收入假说，消费者是根据现在对一生收入的预期选择消费，随着时间的推移，他们改变消费是因为得到了使他们修正预期的消息，消费的变动是对一生收入“意外变动”的反应，所以消费的变动也应该是无法预期的。

我国农村居民边际消费倾向及其变化趋势研究内容摘要:本文通过收集1978～2005年农村居民收入与消费的人均统计数据,采用分段回归的方法对其进行实证研究,结果发现边际消费倾向的变化趋势呈“倒U”型,并对近年来边际消费倾向的大幅度快速下降提出建议。

关键词:边际消费倾向变化趋势政策建议人们用边际消费倾向(MPC)来表示消费对收入的变化,用可支配收入每增加1元时,人们所增加的消费量来计量。

本文采用凯恩斯消费函数模型,借用Eviews 软件对我国农村居民1978～2005年间的边际消费倾向进行实证研究,以揭示农村居民边际消费倾向的特征和变动趋势,并给出相应的经济解释并提出政策性建议。

农村居民消费模型设定与边际消费倾向估计(一)模型设定影响农村居民消费的因素很多,由于受各种条件的限制,通常只引入居民收入一个变量做解释变量,消费模型设定为:Yt=β1+β2Xt+ut其中,Yt为农村居民人均消费支出,Xt为农村人均居民纯收入,ut为随机误差项。

表1是从《中国统计年鉴》收集的中国农村居民1978～2005年的收入与消费数据,数据以1978年为基年进行了可比价的换算。

表1中,Y(单位:元)为农村居民人均实际消费性支出,X(单位:元)为农村居民人均实际纯收入,为了消除价格变动因素对农村居民收入和消费支出的影响,本文采用1978年可比价格计算出的人均纯收入和人均消费支出的数据做回归分析。

表1中的数据X、Y均采用农村消费价格指数,以1978年为基年调整后的数据。

(二)边际消费倾向估计根据表1数据,在Eviews软件中,使用普通最小二乘法估计消费模型,得:Yt=29.1000+0.7659Xt (1)se=(4.7150)(0.0110)t=(6.1718)(71.9560)R2=0.9950、F=5177.668、df=26、DW=0.8055该回归方程可决系数较高,回归系数均显著。

对样本量为28、一个解释变量的模型,在5%显著水平上查DW统计表可知:dL=1.328、dU=1.476,模型中的DW<dL,显然消费模型中有自相关。

中国城乡居民消费函数的建立及比较分析摘要本文尝试建立我国城乡居民消费函数，并从消费函数的角度比较城乡居民的消费、收入状况其差别，从宏观经济方面给出解释说明及为改善状况给出相应的政策建议。

关键词平均消费倾向；边际消费倾向；消费函数；误差修正模型近年来，我国经济出现了有效需求不足，经济疲软的走势，这与我国当前居民的消费不足有着莫大的关系，消费作为拉动经济增长的三大马车之一，分析消费及其影响状况，对从理论上制定相应的经济政策，维持经济的可持续发展有着重要的意义。

同时，我国是一个二元经济结构的国家，城镇与乡村的发展差距较大，消费状况明显不同，通过分析比较城镇与乡村的长期与短期消费状况，可以发现问题，并采取政策促进城乡居民消费并缩小城乡居民消费差距。

1、文献综述消费函数研究最早出现在西方国家，一些经济学家对消费与收入的关系作出不同的模型进行分析。

首先，凯恩斯提出了绝对收入假说，他认为居民当期消费取决于居民的当期收入。

但凯恩斯的消费函数受到了不少的质疑，最著名的是库兹涅茨提出了居民短期消费函数与长期消费函数的矛盾。

接着，杜森贝里提出了相对收入假说，从消费的“示范效应”和“棘轮效应”两方面解释了短期消费函数和长期消费函数的矛盾。

在20世纪50年代中期和70年代中期，莫迪利亚尼与弗里德曼分别提出了生命周期假说和持久收入假说，这两个模型都很好地解释了短期和长期消费函数的矛盾。

我国作为一个新兴的市场经济的国家，直接套用西方的经济消费模型还存在许多的问题，许多统计学家和经济学家试图把我国当前的消费状况与西方消费函数结合在一起，研究适合我国国情的消费函数。

秦朵（1990）研究了居民消费与收入的长期关系，探讨是否存在有效需求上涨及影响短期消费波动的因素。

2、变量选取由于我国市场经济的推行，1985年之前与之后，经济发展规模及居民消费存在较大的波动，本文采用1985年至2010年数据进行统计分析。

除了收入以外，本文还选取以下变量进行建模，城镇居民人均消费支出（rc），城镇居民人均可支配收入（ry），城镇人均金融资产（rs），一年期存款基准利率（rr），城市居民消费水平指数（ri）。