与圆有关的最值问题K

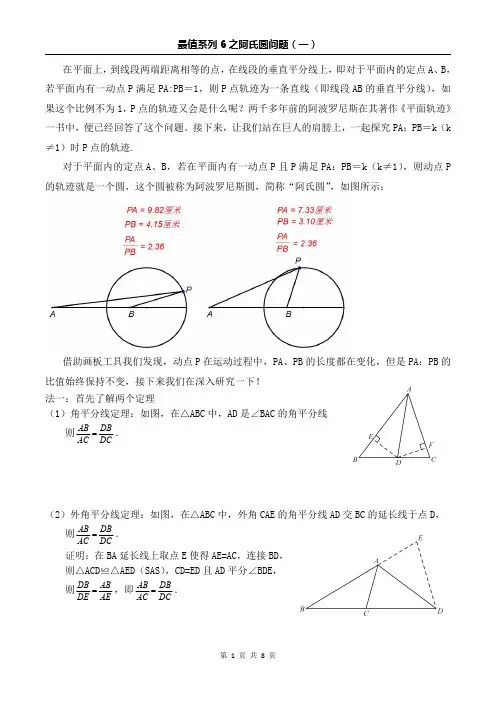
在平面上，到线段两端距离相等的点，在线段的垂直平分线上，即对于平面内的定点A、B，若平面内有一动点P 满足PA:PB＝1，则P 点轨迹为一条直线（即线段AB 的垂直平分线），如果这个比例不为1，P 点的轨迹又会是什么呢？两千多年前的阿波罗尼斯在其著作《平面轨迹》一书中，便已经回答了这个问题。

接下来，让我们站在巨人的肩膀上，一起探究PA：PB＝k（k ≠1）时P 点的轨迹.对于平面内的定点A、B，若在平面内有一动点P 且P 满足PA：PB＝k（k≠1），则动点P 的轨迹就是一个圆，这个圆被称为阿波罗尼斯圆，简称“阿氏圆”，如图所示：借助画板工具我们发现，动点P 在运动过程中，PA、PB 的长度都在变化，但是PA：PB 的比值始终保持不变，接下来我们在深入研究一下！法一：首先了解两个定理（1）角平分线定理：如图，在△ABC 中，AD 是∠BAC 的角平分线则AB DBAC DC=．（2）外角平分线定理：如图，在△ABC 中，外角CAE 的角平分线AD 交BC 的延长线于点D，则AB DBAC DC=．证明：在BA 延长线上取点E 使得AE=AC，连接BD，则△ACD≌△AED（SAS），CD=ED 且AD 平分∠BDE，则DB AB DE AE =，即AB DBAC DC=．接下来开始证明步骤：如图，PA：PB=k，作∠APB的角平分线交AB于M点，根据角平分线定理，MA PA kMB PB==，故M 点为定点，即∠APB的角平分线交AB于定点；作∠APB外角平分线交直线AB于N点，根据外角平分线定理，NA PA kNB PB==，故N点为定点，即∠APB外角平分线交直线AB于定点；又∠MPN=90°，定边对定角，故P点轨迹是以MN为直径的圆．法二：建系不妨将点A、B两点置于x轴上且关于原点对称，设A（-m，0），则B（m，0），设P（x，y），PA=kPB，即：()()()()()()()()222222222222222222222122102201x m y k x m yx m y k x m k yk x y m k m x k mm k mx y x mk++=-+++=-+-+-++-=++-+=-解析式满足圆的一般方程，故P点所构成的图形是圆，且圆心与AB共线．例1.如图，正方形ABCD的边长为4，圆B的半径为2，点P是圆B上一动点，则的最小值为，的最大值为.【答案】最小值为5，最大值为5例2.如图，在Rt△ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C，分别交AC、BC 于D、E 两点，点P 是圆C 上一个动点，则12PA PB +的最小值为__________．【分析】注意到圆C 半径为2，CA=4，连接CP，构造包含线段AP 的△CPA，在CA 边上取点M 使得CM=2，连接PM，可得△CPA∽△CMP，故PA：PM=2:1，即PM=12PA ．【总结】（1）这里为什么是12PA ？答：因为圆C 半径为2，CA=4，比值是1:2，所以构造的是12PA ，也只能构造12PA ．（2）如果问题设计为PA+kPB 最小值，k 应为多少？答：根据圆C 半径与CB 之比为2:3，k 应为23．例3.如图，在ABC ∆中，∠ACB=90°，BC=12，AC=9，以点C 为圆心，6为半径的圆上有一个动点D．连接AD、BD、CD，则2AD+3BD 的最小值是．【分析】首先对问题作变式2AD+3BD=233AD BD ⎛⎫+ ⎪⎝⎭，故求23AD BD +最小值即可．考虑到D 点轨迹是圆，A 是定点，且要求构造23AD ，条件已经足够明显．当D 点运动到AC 边时，DA=3，此时在线段CD 上取点M 使得DM=2，则在点D 运动过程中，始终存在23DM DA =．问题转化为DM+DB 的最小值，直接连接BM，BM 长度的3倍即为本题答案．例4.如图，半圆的半径为1，AB为直径，AC、BD为切线，AC＝1，BD＝2，点P为弧AB上一动的最小值.解：如图所示，连接PB、CO，AD与CO相交于点M，当A、P、D的值最小.∵AB＝BD＝2,BD是⊙O的切线,∴∠ABD＝90º,∠BAD＝∠D＝45º,∵AB是⊙O直径,∴∠APB＝90º,∴∠PAB＝∠PBA＝45º,∴PA＝PB,PO⊥AB,∵AC是⊙O的切线,∴AC⊥AB,∴AC∥PO,∠CAO＝90º∵AC＝PO＝1,∴四边形AOPC是平行四边形,而OA＝OP,∠CAO＝90º,∴四边形AOPC是正方形,PC＋PD＝PM＋PD＝DM,∵DM⊥OC,PC＋PD的值最小，最小值为.练习题部分：1.如图，在平面直角坐标系中，点A（4，0），B（4，4），点P在半径为2的圆O上运动，则的最小值是.，，MO＝2，∠POM＝90º，Q则的最小值为.3.如图，在平面直角坐标系中，A（2，0）、B（0，2）、C（4，0）、D（3，2），P是△AOB外部的第一象限内一动点，且∠BPA＝135º，则2PD＋PC的最小值是.4．（1）如图1，已知正方形ABCD的边长为4，圆B的半径为2，点P是圆B上的一个动点，的最小值为，PD﹣PC的最大值为.（2）如图2，已知正方形ABCD的边长为9，圆B的半径为6，点P是圆B上的一个动点，那么PD＋的最小值为，PD﹣PC的最大值为．（3）如图3，已知菱形ABCD的边长为4，∠B＝60°，圆B的半径为2，点P是圆B上的一个动点，那么PD＋PC的最小值为，PD﹣PC的最大值为．5．如图，在△ACE中，CA＝CE，∠CAE＝30°，⊙O经过点C，且圆的直径AB在线段AE上．（1）证明：CE是⊙O的切线；（2）若△ACE中AE边上的高为h，试用含h的代数式表示⊙O的直径AB；（3）设点D是线段AC上任意一点（不含端点），连接OD，当CD＋OD的最小值为6时，求⊙O的直径AB的长．6.如图，在Rt△ABC中，∠A＝30°，AC＝8，以C为圆心，4为半径作⊙C．（1）试判断⊙C与AB的位置关系，并说明理由；（2）点F是⊙C上一动点，点D在AC上且CD＝2，试说明△FCD∽△ACF；（3）点E是AB边上任意一点，在（2）的情况下，试求出EF＋FA的最小值.7.如图，点A、B上，且OA＝OB＝6，且OA⊥OB，点C是OA的中点，点D在OB上，且OD＝4，动点P（1）求2PC＋PD的最小值；（2）求2PC＋3PD的最小值.8.问题提出：如图1，在等边△ABC中，AB＝12，⊙C半径为6，P为圆上一动点，连结AP，BP，求AP＋BP的最小值．（1）尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP，在CB上取点D，使CD＝3，则有＝＝，又∵∠PCD＝∠BCP，∴△PCD∽△BCP，∴＝，∴PD＝BP，∴AP＋BP＝AP＋PD．请你完成余下的思考，并直接写出答案：AP＋BP的最小值为．（2）在“问题提出”的条件不变的情况下，AP＋BP的最小值为．（3）自主探索：如图3，矩形ABCD中，BC＝7，AB＝9，P为矩形内部一点，且PB＝3，AP ＋PC的最小值为．（4）拓展延伸：如图4，扇形COD中，O为圆心，∠COD＝120°，OC＝4，OA＝2，OB＝3，点P是上一点，求2PA＋PB的最小值，画出示意图并写出求解过程．（5）拓展延伸：已知扇形COD中，∠COD＝90°，OC＝6，OA＝3，OB＝5，点P是上一点，求2PA＋PB的最小值．。

与圆有关的最值问题一、考情分析通过对近几年的高考试题的分析比较发现,高考对直线与圆的考查,呈现逐年加重的趋势,与圆有关的最值问题,更是高考的热点问题.由于圆既能与平面几何相联系,又能与圆锥曲线相结合,命题方式比较灵活,故与圆相关的最值问题备受命题者的青睐. 二、经验分享1. 与圆有关的最值问题的常见类型及解题策略(1)与圆有关的长度或距离的最值问题的解法．一般根据长度或距离的几何意义，利用圆的几何性质数形结合求解．(2)与圆上点(x ，y )有关代数式的最值的常见类型及解法．①形如u ＝y －bx －a 型的最值问题，可转化为过点(a ，b )和点(x ，y )的直线的斜率的最值问题；②形如t ＝ax ＋by 型的最值问题，可转化为动直线的截距的最值问题；③形如(x －a )2＋(y －b )2型的最值问题，可转化为动点到定点(a ，b )的距离平方的最值问题． 2.与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面．解决此类问题的主要思路是利用圆的几何性质将问题转化 三、知识拓展1.圆外一点P 到圆C 上点的距离距离的最大值等于，最小值等于PC r -.2.圆C 上的动点P 到直线l 距离的最大值等于点C 到直线l 距离的最大值加上半径，最小值等于点C 到直线l 距离的最小值减去半径.3.设点M 是圆C 内一点，过点M 作圆C 的弦，则弦长的最大值为直径，最小的弦长为.四、题型分析(一) 与圆相关的最值问题的联系点 1.1 与直线的倾斜角或斜率的最值问题利用公式k ＝tan α(α≠90°)将直线的斜率与倾斜角紧密联系到一起,通过正切函数的图象可以解决已知斜率的范围探求倾斜角的最值,或者已经倾斜角的范围探求斜率的最值.处理方法：直线倾斜角的范围是[0,π),而这个区间不是正切函数的单调区间,因此根据斜率求倾斜角的范围时,要分⎣⎢⎡⎭⎪⎫0，π2与⎝ ⎛⎭⎪⎫π2，π两种情况讨论．由正切函数图象可以看出,当α∈⎣⎢⎡⎭⎪⎫0，π2时,斜率k ∈[0,＋∞)；当α＝π2时,斜率不存在；当α∈⎝ ⎛⎭⎪⎫π2，π时,斜率k ∈(－∞,0)． 【例1】坐标平面内有相异两点,经过两点的直线的的倾斜角的取值范围是( ).A ．,44ππ⎡⎤-⎢⎥⎣⎦ B ． C ．D ．3,44ππ⎡⎤⎢⎥⎣⎦ 【答案】C 【解析】,且0AB k ≠.设直线的倾斜角为α,当01AB k <≤时,则,所以倾斜角α的范围为04πα≤≤.当时,则,所以倾斜角α的范围为34παπ≤<. 【点评】由斜率取值范围确定直线倾斜角的范围要利用正切函数y ＝tan x 的图象,特别要注意倾斜角取值范围的限制；求解直线的倾斜角与斜率问题要善于利用数形结合的思想,要注意直线的倾斜角由锐角变到直角及由直角变到钝角时,需依据正切函数y ＝tan x 的单调性求k 的范围． 【小试牛刀】若过点的直线与圆224x y +=有公共点,则该直线的倾斜角的取值范围是（ ）A ．0 6π⎛⎫ ⎪⎝⎭，B ．0 3π⎡⎤⎢⎥⎣⎦， C. 0 6π⎡⎤⎢⎥⎣⎦， D ．0 3π⎛⎤ ⎥⎝⎦， 【答案】B【解析】当过点的直线与圆224x y += 相切时,设斜率为k ,则此直线方程为,即.由圆心到直线的距离等于半径可得,求得0k =或k =故直线的倾斜角的取值范围是[0,]3π,所以B 选项是正确的.1.2 与距离有关的最值问题在运动变化中,动点到直线、圆的距离会发生变化,在变化过程中,就会出现一些最值问题,如距离最小,最大等.这些问题常常联系到平面几何知识,利用数形结合思想可直接得到相关结论,解题时便可利用这些结论直接确定最值问题.【例2】 过点()1,2M 的直线l 与圆C ：交于,A B 两点,C 为圆心,当ACB ∠最小时,直线l 的方程是 ． 答案:解析：要使ACB ∠最小,由余弦定理可知,需弦长AB 最短.要使得弦长最短,借助结论可知当()1,2M 为弦的中点时最短.因圆心和()1,2M 所在直线的,则所求的直线斜率为1-,由点斜式可得.【点评】与圆有关的长度或距离的最值问题的解法．一般根据长度或距离的几何意义,利用圆的几何性质数形结合求解．此题通过两次转化,最终转化为求过定点的弦长最短的问题. 【例3】若圆C ：关于直线对称,则由点(,)a b 向圆C 所作的切线长的最小值是（ ）A ．2B ．3C ．4D ．6 【答案】C【解析】圆C ：化为（x+1）2+（y-2）2=2,圆的圆心坐标为（-1,2．圆C ：关于直线2ax+by+6=0对称,所以（-1,2）在直线上,可得-2a+2b+6=0,即a=b+3．点（a,b ）与圆心的距离,,所以点（a,b ）向圆C 所作切线长：当且仅当b=-1时弦长最小,为4【点评】与切线长有关的问题及与切线有关的夹角问题,解题时应注意圆心与切点连线与切线垂直,从而得出一个直角三角形．【小试牛刀】【安徽省合肥一中、马鞍山二中等六校教育研究会2019届高三第二次联考】已知抛物线上一点到焦点的距离为，分别为抛物线与圆上的动点，则的最小值为（ ） A ．B ．C ．D ．【答案】D 【解析】由抛物线焦点在轴上，准线方程，则点到焦点的距离为，则，所以抛物线方程：，设，圆，圆心为，半径为1，则，当时，取得最小值，最小值为，故选D.1.3 与面积相关的最值问题与圆的面积的最值问题,一般转化为寻求圆的半径相关的函数关系或者几何图形的关系,借助函数求最值的方法,如配方法,基本不等式法等求解,有时可以通过转化思想,利用数形结合思想求解.【例4】 在平面直角坐标系中,,A B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线相切,则圆C 面积的最小值为（ ）A.45πB.34πC.(6π-D.54π 【答案】A 【解析】设直线l ：.因为,所以圆心C 的轨迹为以O 为焦点,l 为准线的抛物线.圆C 半径最小值为,圆C 面积的最小值为选A.【例5】动圆C 经过点(1,0)F ,并且与直线1x =-相切,若动圆C 与直线总有公共点,则圆C的面积（ ）A ．有最大值8πB ．有最小值2πC ．有最小值3πD ．有最小值4π 【答案】D【解析】设圆心为(,)a b ,半径为r ,,即,即214a b =,∴圆心为21(,)4b b ,2114r b =+,圆心到直线的距离为,∴或2b ≥,当2b =时,,∴.【小试牛刀】【山东省恒台第一中学2019届高三上学期诊断】已知O 为坐标原点，直线．若直线l 与圆C 交于A ，B 两点，则△OAB 面积的最大值为（ ）A ．4B ．C ．2D ．【答案】C 【解析】由圆的方程可知圆心坐标，半径为2，又由直线，可知，即点D 为OC 的中点， 所以,设，又由，所以，又由当，此时直线，使得的最小角为，即当时，此时的最大值为2，故选C 。

利用数形结合思想探究与圆有关的最值问题
在运动变化中，动点到直线、圆的距离会发生变化，在变化过程中，与圆有关的长度最值问题有以下题型：
思路分析：
已知点满足与圆有关的某个条件，求圆中参数或点的坐标的取值范围问
的不等式，即可解出
=45，
2
45
=
2
在运动变化中，动点到直线、圆的距离会发生变化，在变化过程中，就会
与圆有关的长度最值问题有以下题型：
到圆上距离最近为
③直线与圆相离，则圆上点到直线的最短距离为圆心到直线的距离
动点距离问题，利用两点间距离公式转化二元函数的最值问题，利用消元法转
+，最小值的距离为d，圆半径为r，则圆上的点到直线的距离的最大值为d r
时可以通过转化思想，利用数形结合思想求解
圆上点的坐标满足关系式的最值或取值范围问题
例5 实数x 、y 满足22326x y x +=，则22y x +的最大值为 . 用消元法化为关于.
法二：令
2
y+
=k，
d－r.
纵观近几年高考对于圆的的考查，重点放在与圆相关的最值问题上,主要考查与圆相关的参数范围问题和圆相关的长度或面积的最值问题.要求学生有较强的数形结合能力、转化与化归意识和准确的计算能力，才能顺利解答.从实际教学来看，这部分知识是学生掌握最为模糊，看到就头疼的题目.分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.。

专题09圆中的范围与最值问题【知识梳理】涉及与圆有关的最值，可借助图形性质，利用数形结合求解．一般地：（1）形如ax by --=μ的最值问题，可转化为动直线斜率的最值问题．（2）形如by ax t +=的最值问题，可转化为动直线截距的最值问题．（3）形如22)()(b y a x m -+-=的最值问题，可转化为曲线上的点到点（a ，b ）的距离平方的最值问题解决圆中的范围与最值问题常用的策略：（1）数形结合（2）多与圆心联系（3）参数方程（4）代数角度转化成函数值域问题【专题过关】【考点目录】考点1：斜率型考点2：直线型考点3：距离型考点4：周长面积型考点5：长度型【典型例题】考点1：斜率型1．（2021·江西·高二期中（理））已知圆22:(1)1C x y +-=，点(3,0)A 在直线l 上，过直线l 上的任一点P 引圆C 的两条切线，若切线长的最小值为2，则直线l 的斜率k =（）A ．2B ．12C ．2-或12D ．2或12-【答案】C【解析】圆22:(1)1C x y +-=的圆心为(0,1)C ，半径为1，因为切线长的最小值为2，所以min ||PC =所以圆心C 到直线l :(3)l y k x =-，即30kx y k --=，所以圆心(0,1)C 到直线30kx y k --==，=22320k k +-=，解得12k =或2k =-.故选：C2．（2021·山东泰安·高二期中）设点(),P x y 是曲线y =上的任意一点，则24y x --的取值范围是（）A ．1205⎡⎤⎢⎥⎣⎦，B ．21255⎡⎤⎢⎥⎣⎦，C ．[]0,2D ．2,25⎡⎤⎢⎥⎣⎦【答案】B【解析】曲线y =表示以()1,0为圆心，2为半径的下半圆，如图所示：24y x --可表示点(),P x y 与点()4,2Q 连线斜率k 当直线PQ 与圆相切时：设直线方程为()24y k x -=-，即420kx y k --+=圆心到直线距离2d ==，解得125k =或0k =，又0y ≤，所以125k =，当直线经过点()1,0A -时，2245y x -=-，综上21255k ⎡⎤∈⎢⎥⎣⎦，故选：B.3．（2021·上海市控江中学高二期中）若直线:3(1)l y k x -=-与曲线:C y =不同公共点，则实数k 的取值范围是（）A ．4,3⎛⎫+∞ ⎪⎝⎭B ．43,32⎛⎤⎥⎝⎦C ．40,3⎛⎫ ⎪⎝⎭D ．43,32⎛⎫ ⎪⎝⎭【答案】B【解析】直线:3(1)l y k x -=-过定点(1,3)，曲线:C y =(0,0)为圆心，1为半径，且位于y 轴上半部分的半圆，如图所示当直线l 过点(1,0)-时，直线l 与曲线有两个不同的交点，此时03k k =-+-，解得32k =.当直线l 和曲线C 相切时，直线和半圆有一个交点，圆心(0,0)到直线:3(1)l y k x -=-的距离1d ==，解得43k =结合图像可知，当4332k <≤时，直线l 和曲线C 恰有两个交点故选：B4．（多选题）（2021·湖北宜昌·高二期中）实数,x y ，满足22++20x y x =，则下列关于1yx -的判断正确的是（）A ．1yx -B ．1yx -的最小值为C ．1y x -的最大值为3D ．1y x -的最小值为33-【答案】CD【解析】由题意可得方程22++20x y x =为圆心是()10C -，，半径为1的圆，则1yx -为圆上的点与定点()10P ，的斜率的值，设过()10P ，点的直线为()+1y k x =，即+0kx y k -=，则圆心到到直线+0kx y k -=的距离d r =1=，整理可得231k =，解得33k =±，所以1y x ⎡∈⎢-⎣⎦，即1y x -33-.故选：CD.5．（2021·广东·兴宁市叶塘中学高二期中）已知实数x ，y 满足方程22410x y x +-+=，求：(1)yx的最大值；(2)22x y +的最小值．【解析】(1)()222241023x y x x y +-+=⇒-+=，圆心()2,0，半径r =。

圆的最值问题一圆心到定直线的距离的最值问题例1 设P 是直线043:=-y x l 上的动点，PA,PB 是圆012222=+--+y x y x 的两条切线，C 是圆心，那么四边形PACB 的最小值是_____________.变式:已知）（y x P ,是直线)0(04>=++k y kx 上一动点，PA,PB 是圆：0222=-+y y x 的两条切线，A,B 是切点，若四边形PACB 最小面积是2，则k=_____________。

二圆上动点到定直线的距离的最值问题例2 圆012222=+--+y x y x上的点到直线2=-y x 距离的最大值是_______________。

变式：已知P 是圆122=+y x上的一点，Q 是直线052:=-+y x l 上的一点，求PQ 最小值。

三圆的切线长最值问题例3 从点P(m,3)向圆C:()()12222=+++y x 引切线，则切线长的最小值为_____________。

变式：由直线2+=x y 上的点向圆()()12y 422=++-x 引切线，怎切线的最小值为____________。

四与圆的弦长有关的最值问题例4 在圆06222=--+y x y x 内，过点E(0,1)的最长弦和最短弦分别是AC 和BD ，则四边形ABCD 的面积为_______________。

变式：已知圆O 的方程是01028y 22=+--+y x x，过点M(3,0)的最短弦所在的直线方程是_____。

五圆中“斜率”最值问题例3 在平面直角坐标系xOy 中，圆C 的方程为0158y 22=+-+x x 。

若直线2y -=kx 上至少存在一点，使得以改点为圆心，1为半径的圆与圆有公共点，则k 的最大值是_________________。

变式：如果实数x,y 满足等式(),1222=+-y x 那么13y -+x 的取值范围________________。

与圆相关的最值（取值范围）问题，附详尽答案姓名1. 在座标系中，点 A 的坐标为 (3， 0)，点 B 为 y 轴正半轴上的一点，点C 是第一象限内一点，且 AC=2．设 tan ∠ BOC=m ，则 m 的取值范围是 _________．2. 如图，在边长为 1 的等边 △ OAB 中，以边 AB 为直径作 ⊙ D ，以 O 为圆心 OA 长为半径作圆 O ， C 为半圆 AB 上不与 A 、 B 重合的一动点，射线AC 交 ⊙ O 于点 E ， BC=a ， AC=b ．（ 1）求证： AE=b+ a ；（ 2）求 a+b 的最大值；（3）若 m 是对于 x 的方程： x 2+ax=b 2+ab 的一个根，求 m 的取值范围．3. 如图，∠ BAC=60 °，半径长为 1 的圆 O 与∠ BAC 的两边相切，P 为圆 O 上一动点，以 P 为圆心， PA 长为半径的圆 P 交射线 AB 、AC 于 D 、 E 两点，连结DE ，则线段 DE 长度的最大值为 (). A ．3 B ． 63 3C ．D ．3 324.如图， A 点的坐标为（﹣ 2， 1），以 A 为圆心的⊙A 切 x 轴于点 B， P（ m， n）为⊙A 上的一个动点，请研究 n+m 的最大值．5.如图，在Rt△ ABC中，∠ ACB=90 °， AC=4， BC=3，点 D 是平面内的一个动点，且 AD=2，M 为 BD 的中点，在 D 点运动过程中，线段CM 长度的取值范围是.6.如图是某种圆形装置的表示图，圆形装置中，⊙ O 的直径 AB=5，AB 的不一样侧有定点 C 和动点 P，tan ∠ CAB= ．其运动过程是：点 P 在弧 AB 上滑动，过点 C 作 CP 的垂线，与PB的延伸线交于点Q．（1）当 PC=时，CQ与⊙O相切；此时CQ=．（2）当点 P 运动到与点 C 对于 AB 对称时，求 CQ的长；（3）当点 P 运动到弧 AB 的中点时，求 CQ 的长．（4）在点 P 的运动过程中，线段CQ 长度的取值范围为。

与圆有关的最值问题与代数表达式的几何意义1．代数表达式的几何意义 ①y －bx －a 表示动点(x ，y )与定点(a ，b )连线的斜率．②x 2＋y 2表示动点(x ，y )与原点(0,0)距离的平方．x －a 2＋y －b 2表示动点(x ，y )与定点(a ，b )之间的距离．③求2x ＋y 的取值范围时，可令t ＝2x ＋y ，则y ＝－2x ＋t ，t 表示直线y ＝－2x ＋t 在y 轴上的截距．求3x －2y 的取值范围时，令t ＝3x －2y ，则y ＝32x －t 2，则－t 2表示直线y ＝32x －t 2在y 轴上的截距． 2．与圆有关的最值问题①点P (x ，y )是⊙C 上的动点，Q (a ，b )是定点，求y x ，y －bx －a ，x 2＋y 2，(x －a )2＋(y －b )2,2x ＋y 的取值范围时，利用代数表达式的几何意义，数形结合求解．②点P (x ，y )是⊙C 上的动点，l 是直线，Q 是直线l 上的动点，求|PQ |或P 到l 的距离的最值时，利用数形结合法求解．③⊙C 经过定点A ，圆心C 在直线l 上运动，求半径最小的圆或求经过两定点A 、B 的最小的圆，用数形结合法讨论求解．④P 在⊙C 内，求经过点P 的直线与圆相交最短弦长，用数形结合法求解． ⑤P 、Q 分别在⊙C 1与⊙C 2上运动，求|PQ |的最值，用数形结合讨论求解． 典例1 (2016·湖北襄阳枣阳二中高三期中)已知点P (x ，y )在圆x 2＋y 2－6x －6y ＋14＝0上.(1)求y x的最大值和最小值；(2)求x 2＋y 2＋2x ＋3的最大值与最小值．[解析] 圆方程化为(x －3)2＋(y －3)2＝4，圆心C (3,3)，半径r ＝2．(1)y x 表示圆上点(x ，y )与原点(0,0)连线的斜率；设y x＝k ，显然当直线y ＝kx 与⊙C 相切时，k 取到最大值与最小值，由|3k －3|1＋k 2＝2，得k ＝9±2145． ∴yx 的最大值为9＋2145，最小值为9－2145． (2)x 2＋y 2＋2x ＋3＝(x ＋1)2＋y 2＋2表示圆上点P (x ，y )与定点A (－1,0)，连线段长度d 的平方加上2．∵|AC |＝5，∴3≤d ≤7∴所求最小值为11．典例2 已知圆M ：x 2＋y 2＝10和圆N ：x 2＋y 2＋2x ＋2y －14＝0，求过两圆交点，且面积最小的圆的方程．[解析] 设两圆交点为A ，B ，则以AB 为直径的圆就是所求的圆．直线AB 的方程为x ＋y －2＝0．两圆圆心连线的方程为x －y ＝0．解方程组⎩⎨⎧x ＋y －2＝0，x －y ＝0.得圆心坐标为(1,1)．圆心M (0,0)到直线AB 的距离为d ＝ 2弦AB 的长为|AB |＝2102－22＝4 2所以所求圆的半径为22．所以所求圆的方程为(x －1)2＋(y －1)2＝8．。

3.圆最值问题一．重要结论1.圆中与距离最值有关的常见的结论：结论1.圆外一点A 到圆上距离最近为AO r ，最远为AO r ；结论2.过圆内一点的弦最长为圆的直径，最短的弦为与过该点的直径垂直的弦；结论3.直线与圆相离，则圆上点到直线的最短距离为圆心到直线的距离d r ,最近为d r ；2.圆中与面积有关的最值结论：结论4.圆的内接三角形面积最大当且仅当其为等边三角形；结论5.过圆外一点P 向圆O 引两条切线，切点记为B A ,，则四边形ABPO 面积的最值等价于圆心到点P 的距离最值.3.圆中与角度有关的最值问题.结论6.圆上两点与圆外一点的连线的夹角（圆外一点为顶点）中，以这两条直线为切线时最大.结论7.圆上一点、圆心与圆外一点连线的夹角（圆外一点为顶点）中，以这条直线为切线时最大.结论8.圆上一点、圆外两点连线的夹角（圆外一点为顶点）中，以这条直线为切线时最大.结论9.圆内两点，圆上一点（圆上点为顶点）的最大夹角问题（米勒圆问题）.4.其他与圆有关的最值问题结论10．两个动点分别在两条平行线上运动,这两个动点间的最短距离为两条平行线间的距离.二．强化练习1．已知圆P 的方程为22680x y x y ，过点 1,2M 的直线与圆P 交于A ，B 两点，则弦AB 的最小值为（）A．B．10C．D．52．在圆22:230M x y x 中，过点 0,1E 的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为（）A．B．C．D．3．已知点(,)P x y 是圆2264120x y x y 上的动点，则x y 的最大值为（）A．5B．5C．6D．54．已知方程22220x y kx y k 表示的圆中，当圆面积最小时，此时k （）A．-1B．0C．1D．25．直线 1210m x my m 与圆229x y 交于,M N 两点，则弦长MN 的最小值为（）A．1B．26．设A 是圆22(1)9x y 上的动点，PA 是圆的切线，且4PA ，则点P 到点 5,8Q 距离的最小值为（）A．4B．5C．6D．157．已知P 为抛物线24y x 上一个动点，Q 为圆 22241x y 上一个动点，那么点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是（）A．6B．5C．4D．38．已知点M ，N 分别在圆 221:129C x y 与圆 222:2864C x y 上，则MN 的最大值为（）11B．1711D．159．已知P 是半圆C x 上的点，Q 是直线10x y 上的一点，则PQ 的最小值为（）1110.（2021新高考1卷）．已知点P 在圆 225516x y 上，点 4,0A ， 0,2B ，则（）A．点P 到直线AB 的距离小于10B．点P 到直线AB 的距离大于2C．当PBA 最小时，PBD．当PBA 最大时，PB 参考答案1．已知圆P 的方程为22680x y x y ，过点 1,2M 的直线与圆P 交于A ，B 两点，则弦AB 的最小值为（）A．B．10C．D．5【答案】A2．在圆22:230M x y x 中，过点 0,1E 的最长弦和最短弦分别为AC 和BD ，则四边形ABCD 的面积为（）A．B．C．D．【答案】B3．已知点(,)P x y 是圆2264120x y x y 上的动点，则x y 的最大值为（）A．5B．5C．6D．5【答案】A4．已知方程22220x y kx y k 表示的圆中，当圆面积最小时，此时k （）A．-1B．0C．1D．2【答案】B5．直线 1210m x my m 与圆229x y 交于,M N 两点，则弦长MN 的最小值为（）A．1B．2【答案】D6．设A 是圆22(1)9x y 上的动点，PA 是圆的切线，且4PA ，则点P 到点 5,8Q 距离的最小值为（）A．4B．5C．6D．15【答案】B7．已知P 为抛物线24y x 上一个动点，Q 为圆 22241x y 上一个动点，那么点P到点Q 的距离与点P 到抛物线的准线距离之和的最小值是（）A．6B．5C．4D．3【答案】C8．已知点M ，N 分别在圆 221:129C x y 与圆 222:2864C x y 上，则MN的最大值为（）11 B．1711D．15【答案】C9．已知P 是半圆C x 上的点，Q 是直线10x y 上的一点，则PQ 的最小值为（）2112D．22【答案】D 10．ACD解析：圆 225516x y 的圆心为 5,5M ，半径为4，直线AB 的方程为142x y，即240x y ，圆心M 到直线AB4 ，所以，点P 到直线AB 的距离的最小值为425 ，最大值为4105，A 选项正确，B 选项错误；如下图所示：当PBA 最大或最小时，PB 与圆M 相切，连接MP 、BM ，可知PM PB ，BM4MP ，由勾股定理可得BP CD 选项正确.故选：ACD.多圆最值问题研究一．基本原理1.将军饮马模型：如图，动点C 为直线l 上一点，B A ,为直线l 一侧的两个定点，那么CA CB 的最小值即为做点B 关于l 的对称点'B ，然后连接'BB 后其长度.2.三角不等式：任意两边之和大于等于第三边，任意两边之差小于等于第三边，取等条件当且仅当三点共线.如图动点P 为直线l 上一点，B A ,为直线l 一侧的两个定点，那么P A PB 的最大值当且仅当B A P ,,三点共线.倘若B A ,在l 两侧，则需先利用对称将其搬到一侧再寻找最大值！此时，P A PB 的最小值为0，即P 为AB 中垂线与l 的交点.总结：“和最小，化异侧，差最大，转同侧”二．典例分析1.距离和的最小值（公众号：凌晨讲数学）例1．已知圆221:430C x y y ，圆222:6260C x y x y ，M N ，分别为圆1C 和圆2C 上的动点，P 为直线:1l y x 上的动点，则||MP NP 的最小值为A．3 B．333解析：由圆 221:21C x y ，圆 222314C x y ，可知圆1C 圆心为 0,2 ，半径为1，如图，圆2C 圆心为 3,1 ，半径为2，圆1C 关于直线:1l y x 的对称圆为圆 221':311C x y ，连结12'C C ，交l 于P ，则P 为满足使PM PN 最小的点，此时M 点为1'PC 与圆1'C 的交点关于直线l 对称的点，N 为2PC 与圆2C 的交点，最小值为 12'21C C ，而12'C C ，PM PN 的最小值为3 ，故选A.2.距离差的最大值（公众号：凌晨讲数学）例2．已知圆 221:111C x y ，圆 222:459C x y ，点M 、N 分别是圆1C 、圆2C 上的动点，点P 为x 轴上的动点，则PN PM 的最大值是（）A．4B．9C．7D．2解析：圆 221:111C x y 的圆心为 11,1C ，半径为1，圆 222:459C x y 的圆心为 24,5C ，半径为3．max min maxPN PM PN PM ∵，又2max 3PN PC ，1min1PMPC ，2121max314PN PMPC PC PC PC ．点 24,5C 关于x 轴的对称点为24,5C ，2121125PC PC PC PC C C，所以，max549PN PM ，故选：B．3.逆用阿波罗尼斯圆1.阿氏圆定义：已知平面上两点B A ,，则所有满足1,|||| PB P A 的动点P 的轨迹是一个以定比为n m :内分和外分定线段AB 的两个分点的连线为直径的圆.若)0,(),0,(b B a A ,则圆的半径为|||1|2AB ，圆心为)0|,|11(22AB .（公众号：凌晨讲数学）2.结论：已知圆222)()(r b y a x 上任意一点P 和坐标轴上任意两点B A ,，求形如)(PB P A PB P A 的最值问题，可逆用阿氏圆转化为三点共线最值计算.例3．已知圆C 是以点 2,M 和点 6,N 为直径的圆，点P 为圆C 上的动点，若点2,0A ，点 1,1B ，则2PA PB 的最大值为（）B．4C．8解析：由题设，知：(4,0)C 且||8MN ，即圆C 的半径为4，∴圆C ：22(4)16x y ，如上图，坐标系中(4,0)D 则24OD AC CP OC ，∴12AC PC CP DC ，即△APC △PCD ，故12PA PD ，（亦可逆用阿氏圆，其实就是阿氏圆的几何推导）.∴2||||PA PB PD PB ，在△PBD 中||||||PD PB BD ，∴要使||||PD PB 最大，,,P B D 共线且最大值为||BD 的长度.∴||BD 故选：A例4．在平面直角坐标系xOy 中，点P 在圆22:(8)16C x y -+=上运动，(6,0),(6,1),A B 则2PB PA 的最小值为（）B．6C．D．2解析：P 为圆C 上任意一点，圆的圆心 8,0C ，半径4r ，如下图所示，4PC ∵，8OC ，2AC 12AC PC PC OC ，PAC OPC 12PA OP，即2OP PA ，2PB PA PB OP ，又PB OP OB （当且仅当P 为线段OB与圆C 的交点时取等号），2PB PA OB 2PB PA本题正确选项：A三．练习题（公众号：凌晨讲数学）1．已知,P Q 分别是直线:20l x y 和圆22:1C x y 上的动点，圆C 与x 轴正半轴交于点(1,0)A ，则PA PQ 的最小值为2B．251210122．已知P ，Q 分别是圆 22:48C x y ，圆 22:41D x y 上的动点，O 是坐标原点，则22PQ PO的最小值是______．3．平面直角坐标系中，点3,3A 、 3,3B 、23,0C ，动点P 在ABC 的内切圆上，则12PC PA 的最小值为_________.4．在平面直角坐标系xOy 中，若(0,1)A ，点B 是圆:C 22230x y x 上的动点，则2AB BO 的最小值为__________.。

与圆有关的最值问题-高三数学备考练习近几年高考试题分析发现，与圆有关的最值问题是高考热点问题之一。

这类问题既能与平面几何相联系，又能与圆锥曲线相结合，命题方式比较灵活。

解决这类问题的主要思路是利用圆的几何性质将问题转化。

常见类型包括与圆有关的长度或距离的最值问题和与圆上点(x，y)有关代数式的最值问题。

对于长度或距离的最值问题，一般根据长度或距离的几何意义，利用圆的几何性质数形结合求解。

对于与圆上点(x，y)有关代数式的最值问题，常见类型包括形如u＝x－a型、t＝ax＋by型和(x－a)2＋(y－b)2型。

这些问题可以转化为斜率的最值问题、动直线的截距的最值问题和动点到定点(a，b)的距离平方的最值问题。

与圆有关的最值问题主要表现在求几何图形的长度、面积的最值，求点到直线的距离的最值，求相关参数的最值等方面。

知识拓展包括圆外一点P到圆C上点的距离距离的最大值等于，最小值等于PC-r，圆C上的动点P到直线l距离的最大值等于点C到直线l距离的最大值加上半径，最小值等于点C到直线l距离的最小值减去半径，以及圆C内一点M的弦长的最大值为直径，最小的弦长为圆心角对应的弧长。

解决与圆相关的最值问题的主要思路是利用圆的几何性质将问题转化。

例如，与直线的倾斜角或斜率的最值问题可以利用公式k＝tan(≠90°)将直线的斜率与倾斜角紧密联系到一起，通过正切函数的图象可以解决已知斜率的范围探求倾斜角的最值，或者已经倾斜角的范围探求斜率的最值。

处理方法包括分别讨论斜率的范围和倾斜角的范围。

例6】已知实数x,y满足方程$x^2+y^2-4x+1=0$，求：1) $x$ 的最大值和最小值；2) $y-x$ 的最大值和最小值。

解析】1) 将方程化为标准形式：$(x-2)^2+y^2=3$，得到一个以点 $(2,0)$ 为圆心，半径为 $\sqrt{3}$ 的圆。

由于 $x$ 的取值范围为 $[2-\sqrt{3},2+\sqrt{3}]$，所以$x$ 的最大值为 $2+\sqrt{3}$，最小值为 $2-\sqrt{3}$。

２０２３年９月上半月㊀解法探究㊀㊀㊀㊀圆的最值问题求解四法◉云南省普洱市孟连县第一中学㊀孙宝恩㊀㊀摘要:与圆有关的最值问题是近年来高考数学的热点之一,它着重考查数形结合与转化思想．求圆的最值问题 四化法 的基本思路是,利用平面几何知识,或利用圆的参数方程,或设圆上点的坐标,将其转化为函数的最值问题．关键词:化为斜率法;化为截距法;化为距离法;化为三角函数法㊀㊀与圆有关的最值问题,因为其代数式具有明显的几何意义,所以应优先考虑数形结合法．运用数形结合法求最值,既可以借助图形直观获得简捷解法,又可避免因对限制条件考虑不周造成的失误,还有利于沟通数学各个分支,深化思维,全面提高学生数学综合素质[１]．涉及与圆有关的最值问题,可借助圆的几何性质,并根据代数式的几何意义,利用数形结合思想来求解．一般情况下,求形如t ＝y －bx －a的最值问题,可转化为动直线的斜率问题;求形如t ＝a x ＋b y ＋c 的最值问题,可转化为动直线的截距问题;求形如(x －a )２＋(y －b )２的最值问题,可转化为动点到定点的距离问题．另外,还可以通过建立目标函数求最值．与圆有关的最值问题,既是高中数学中的难点问题,又是近年来高考中的热点题型,因此有必要熟悉和掌握其常用的解题思路与方法．１化为斜率法例１㊀已知实数x ,y 满足方程x ２＋y ２－４x ＋１＝０,求yx的最大值和最小值．解:原方程可化为(x －２)２＋y ２＝３,表示以(２,０)为圆心,３为半径的圆．yx 的几何意义是该圆上一点与原点连线的斜率,所以设yx＝k ,即y ＝k x ．图１当直线y ＝k x 与圆相切时,如图１,斜率k 取最大值或最小值,此时２k －０k ２＋１＝３,解得k ＝ʃ３所以yx的最大值为３,最小值为－３．思路与方法:本题中yx 的几何意义是圆上的点与原点连线的斜率,两切线的斜率为其最值,可由２k －０k ２＋１＝３求切线的斜率,也可将y ＝k x 代入圆的方程,由Δȡ０,求解k 的范围．例２㊀求y ＝１＋s i n x２＋c o s x 的最值．图２解:将原函数式变形为y ＝s i n x －(－１)c o s x －(－２),其几何意义是在直角坐标系中,动点(c o s x ,s i n x )与定点P (－２,－１)连线的斜率．动点P 的轨迹为单位圆(如图２),由图可知,k P B 最小,k P C 最大．显然,k P B ＝０．由t a n θ＝O B P B ＝１２,得t a n øB P C ＝t a n２θ＝２t a n θ１－t a n ２θ＝４３,即k P C ＝４３．故y 的最小值为０,最大值为４３．思路与方法:从本题的解题思路可以归纳 形如f (x )－ag (x )－b 的函数式,可以将其看作点(g (x ),f (x ))与点(b ,a )连线的斜率,这也是最常见的解题方法．２化为截距法例３㊀在圆O :x ２＋y ２＝１上求一点P ,使得过点P 的切线与两条坐标轴所围成的三角形面积最小．解法１:设P (x １,y １),则切线l 为x １x ＋y １y ＝１,即x １x １＋y １y １＝１,截距a ＝１x １,b ＝１y １．所以,过点P 的切线与两坐标轴所围成的三角形面积为S ＝１２a９７Copyright ©博看网. All Rights Reserved.解法探究２０２３年９月上半月㊀㊀㊀b ＝１２１x １ １y １＝１２x １y １ȡ１x ２１＋y ２１＝１１＝１,当且仅当x １＝y １＝２２时,取等号,S 的最小值为１．故所求点P 的坐标为(２２,２２),(２２,－２２),(－２２,－２２),(－２２,２２)．解法２:因为点P 在圆x ２＋y ２＝１上,可设P (c o s φ,s i n φ),所以切线l :x c o s φ＋y s i n φ＝１,其截距a ＝１c o s φ,b ＝１s i n φ．因此,过点P 的切线与两坐标轴所围成的三角形面积为S ＝１２a b ＝１２１c o s φ １s i n φ＝１s i n ２φȡ１．当s i n ２φ＝ʃ１,即φ＝ʃπ４,ʃ３４π时,S 取最小值,且最小值为１．故所求点P 的坐标为(２２,２２),(２２,－２２),(－２２,－２２),(－２２,２２)．思路与方法:本题的两种解法都是将与圆有关的求三角形的最值问题转化为直线与圆相切的截距型问题．通过设点P 的坐标,先求出截距,然后再根据三角形面积公式推出S әȡ１,最后确定点P 的位置．例４㊀设x ,y 满足y ＝－x ２－２x ,求S ＝x ＋y 的最大值和最小值．图３解:y ＝－x ２－２x ＝１－(x ＋１)２,其图象为如图３所示的半圆O ᶄ,S 的最大值与最小值分别是直线y ＝－x ＋S 和半圆O ᶄ有公共点时截距的最大值与最小值．由A (－２,０),k A D ＝－１,得D (０,－２),即S m i n ＝－２．又O ᶄB ＝B C ＝１,所以O ᶄC ＝２,得O C ＝２－１＝O D ᶄ,则点D ᶄ的坐标为(０,２－１),即S m a x ＝２－１．故S 的最大值与最小值分别为２－１,－２．思路与方法:本题是将其转化㊁变形为截距型最值问题,并对半圆㊁直线截距的几何意义进行了由 隐 到 显 的挖掘,其中紧扣 S 的最大值与最小值分别是直线y ＝－x ＋S 和半圆O ᶄ有公共点时截距S的最大值与最小值 是关键．３化为距离法例５㊀在әA B C 中,øA ,øB ,øC 所对的边分别为a ,b ,c ,且c ＝１０,c o s A c o s B ＝b a ＝４３,P 为әA B C的内切圆上的动点,求点P 到顶点A ,B ,C 的距离的平方和的最大值与最小值．解法１:由c o s A c o s B ＝b a ,得c o s A c o s B ＝s i n Bs i n A ,即s i n ２A ＝s i n２B ．在әA B C 中,因为A ʂB ,所以２A ＋２B ＝π,则A ＋B ＝π２,故әA B C 为直角三角形．图４由c ＝１０,b a ＝４３,可得a ＝６,b ＝８．建立如图４所示的平面直角坐标系,设әA B C 的内切圆圆心为O ᶄ,切点分别为D ,E ,F ,则|A D |＋|D B |＋|E C |＝１２(１０＋８＋６)＝１２,内切圆的半径r ＝|E C |＝１２－１０＝２,则内切圆O ᶄ方程为(x －２)２＋(y －２)２＝４．设圆O ᶄ上动点P 的坐标为(x ,y ),则点P 到顶点A ,B ,C 的距离的平方和为S ＝P A ２＋P B ２＋P C ２＝(x －８)２＋y ２＋x ２＋(y －６)２＋x ２＋y ２＝３[(x －２)２＋(y －２)２]－４x ＋７６＝８８－４x ．由点P 在圆上,可知,０ɤx ɤ４,于是S 的最大值为８８,最小值为８８－４ˑ４＝７２．解法２:同解法１,得әA B C 是直角三角形,其内切圆半径r ＝２．设圆上动点P 的坐标为(２＋２c o s α,２＋２s i n α)(０ɤαɤ２π),则点P 到顶点A ,B ,C 的距离的平方和为S ＝P A ２＋P B ２＋P C ２＝(２c o s α－６)２＋(２＋２s i n α)２＋(２＋２c o s α)２＋(２s i n α－４)２＋(２＋２c o s α)２＋(２＋２s i n α)２＝８０－８c o s α．因为０ɤαɤ２π,所以S 的最大值为＝８０＋８＝８８,最小值为＝８０－８＝７２．思路与方法:本题可转化为点到直线的距离型最值问题．解法１是由三角形的边㊁角关系推证出әA B C 为直角三角形,然后建立平角直角坐标系,通过设三角形内切圆,求三角形三边的长度获解;解法２在已知әA B C 为直角三角形的基础上,通过设动点坐标,利用三角函数求出最值．０８Copyright ©博看网. All Rights Reserved.２０２３年９月上半月㊀解法探究㊀㊀㊀㊀例６㊀已知实数x ,y 满足方程x ２＋y ２－４x ＋１＝０,求x ２＋y ２的最大值和最小值．图５解:x ２＋y ２－４x ＋１＝０可化为(x －２)２＋y ２＝３,它表示以C (２,０)为圆心,３为半径的圆．如图５所示,x ２＋y ２表示圆上的一点与坐标原点距离的平方．由平面几何知识可知,在坐标原点和圆心连线与圆的两个交点处取得最大值和最小值．又因为圆心C 到原点的距离为２,所以x ２＋y ２的最大值是(２＋３)２＝７＋４３,x ２＋y ２的最小值是(２－３)２＝７－４３．思路与方法:本题中的x ２＋y ２可看作是圆上的点与原点距离的平方,所以可以借助平面几何知识,利用数形结合法快速求解．４化为三角函数法例７㊀已知圆C :(x －３)２＋(y －４)２＝１和两点A (－m ,０),B (m ,０)(m ＞０)．若圆C 上存在点P ,使得øA P B ＝９０ʎ,则m 的最大值为(㊀㊀)．A．７㊀㊀㊀㊀B ．６㊀㊀㊀㊀C ．５㊀㊀㊀㊀D．４解:设点P (x ０,y ０),则x ０＝３＋c o s θ,y ０＝４＋s i n θ{(θ为参数)．由øA P B ＝９０ʎ,得A P ң B P ң＝０,即(x ０＋m )(x ０－m )＋y ２０＝０,则m ２＝x ２０＋y ２０＝２６＋６c o s θ＋８s i n θ＝２６＋１０s i n (θ＋φ)ɤ３６(其中t a n φ＝３４)．所以０＜m ɤ６,即m 的最大值为６．故选答案:B ．思路与方法:本题是通过建立目标函数来求最值．由于øA P B ＝９０ʎ,则点P 也在以A B 为直径的圆上,因此问题还可转化为两圆有公共点,求m 的最大值,即两圆内切时,m 有最大值６．例８㊀半圆O 的直径为２,A 为直径延长线上一点,O A ＝２,B 为半圆上任意一点,以A B 为一边作等边三角形A B C ．问点B 在什么位置时,四边形O A C B的面积最大,并求这个最大值．图６解:如图６,设øA O B ＝α(０＜α＜π),在әA O B 中,又O B ＝１,O A ＝２,由余弦定理,得A B ２＝O A ２＋O B ２－２O A O B c o s α＝５－４c o s α．设四边形O A C B 的面积为S ,则㊀㊀㊀S ＝１２O A O B s i n α＋３４A B ２＝s i n α＋３４(５－４c o s α)＝５３４＋(s i n α－３c o s α)＝５３４＋２s i n (α－π３),当且仅当s i n (α－π３)＝１,即α＝５π６时,四边形O A C B的面积最大,且最大值为５３４＋２．思路与方法:本题通过运用余弦定理,将与圆有关的四边形面积的最值问题,转化为三角函数问题来求解．从解题过程不难看出,对y ＝a s i n x ＋b c o s x (a ,b ʂ０)引入辅角θ,则y ＝a ２＋b ２s i n (x ＋θ)(其中t a n θ＝ba),其最值一目了然．根据以上典例及 四化法 的运用情况,可以把与圆有关的最值问题大致归纳总结为以下几种类型:①定点与圆上的点的距离的最值题型,可将其转化为定点到圆心的距离ʃ半径 ;②定直线与圆上点的距离的最值题型,可将其转化为 圆心到直线的距离ʃ半径 ;③形如t ＝y －bx －a 的最值题型,可将其转化为动直线的斜率问题(切线处取得最值);④形如t ＝a x ＋b y ＋c 的最值题型,可将其转化为动直线的截距问题(切线处取得最值);⑤形如(x －a )２＋(y －b )２的最值问题,可将其转化为定点到圆上动点的最值问题．圆是一种很规则的图形,解答与圆有关的最值问题很适合采用数形结合法．运用 四化法 解题的关键,是在准确理解题意的基础上进行合理联想和类比,将代数式通过转化㊁变形㊁给予几何解释[２]．上述典型例题的解析可以帮助学生学会从 形 中觅 数 的思路与方法,掌握如何根据图形去寻求数量关系的技巧,能够娴熟地将几何问题代数化,通过不断加强这类题型的解题训练,最终达到触类旁通㊁举一反三㊁开阔思路㊁运用自如㊁综合提高的目的．参考文献:[１]杜超．例谈与圆有关的最值问题[J ]．理科考试研究,２０２１(９):１６Ｇ１８．[２]程会海．与圆有关的最值问题的解题策略例说[J ]．中学数学,２０２２(５):６４Ｇ６５．Z １８Copyright ©博看网. All Rights Reserved.。

与圆有关的3类最值问题1.斜率型最值问题【方法点拨】形如μ＝y －b x －a 型的最值问题，可转化过定点(a ，b)的动直线斜率的最值问题求解． 【典例】已知实数x ，y 满足方程x 2＋y 2－4x ＋1＝0，求y x的最大值和最小值．解：原方程可化为(x －2)2＋y 2＝3，表示以(2,0)为圆心，3为半径的圆．y x的几何意义是圆上一点与原点连线的斜率， 所以设y x＝k ，即y ＝k x . 当直线y ＝k x 与圆相切时(如图)，斜率k 取得最大值或最小值，此时|2k －0|k 2＋1＝3， 解得k ＝± 3.∴y x的最大值为3，最小值为－ 3.【练习】已知圆C ：(x ＋2)2＋y 2＝1，P (x ，y )为圆上任意一点，则y －2x －1的最大值为________． 解析： 设y －2x －1＝k ，即k x －y －k ＋2＝0， 圆心C (－2,0)，r ＝1.当直线与圆相切时，k 有最值，∴|－2k －0－k ＋2|k 2＋1＝1，解得k ＝3±34. ∴y －2x －1的最大值为3＋34. 答案：3＋34【方法点拨】形如μ＝ax ＋by 型的最值问题，常转化为动直线截距的最值问题求解．如本题可令b ＝y －x ，即y ＝x ＋b ，从而将y －x 的最值转化为求直线y ＝x ＋b 的截距的最值问题．另外，此类问题也常用三角代换求解．【典例】已知实数x ，y 满足方程x 2＋y 2－4x ＋1＝0，求y －x 的最大值和最小值．解：y －x 可看作是直线y ＝x ＋b 在y 轴上的截距，如图所示，当直线y ＝x ＋b 与圆相切时，纵截距b 取得最大值或最小值，此时|2－0＋b |2＝3， 解得b ＝－2± 6.所以y －x 的最大值为－2＋6，最小值为－2－ 6.【练习】已知P (x ，y )为圆(x －2)2＋y 2＝1上的动点，则|3x ＋4y －3|的最大值为________．解析：设t ＝3x ＋4y －3，即3x ＋4y －3－t ＝0.由圆心(2,0)到直线3x ＋4y －3－t ＝0的距离d ＝|6－3－t |32＋42≤1， 解得－2≤t ≤8.所以|3x ＋4y －3|max ＝8.答案：8【方法点拨】形如μ＝(x －a )2＋(y －b )2型的最值问题，可转化为动点(x ，y )与定点(a ，b )的距离的平方求最值．【典例】已知实数x ，y 满足方程x 2＋y 2－4x ＋1＝0，求x 2＋y 2的最大值和最小值．解：如图所示，x 2＋y 2表示圆上的一点与原点距离的平方，由平面几何知识知，在原点和圆心连线与圆的两个交点处取得最大值和最小值． 又圆心到原点的距离为(2－0)2＋(0－0)2＝2，所以x 2＋y 2的最大值是(2＋3)2＝7＋43，x 2＋y 2的最小值是(2－3)2＝7－4 3.【练习】设点P (x ，y )是圆：x 2＋(y －3)2＝1上的动点，定点A (2,0)，B (－2,0)，则P A ―→·PB ―→的最大值为________．解析：由题意，知P A ―→＝(2－x ，－y )，PB ―→＝(－2－x ，－y )，所以P A ―→·PB ―→＝x 2＋y 2－4，由于点P (x ，y )是圆上的点，故其坐标满足方程x 2＋(y －3)2＝1，故x 2＝－(y －3)2＋1，所以P A ―→·PB ―→＝－(y －3)2＋1＋y 2－4＝6y －12.易知2≤y ≤4，所以，当y ＝4时，P A ―→·PB ―→的值最大，最大值为6×4－12＝12.答案：12。