特殊
(如图所示)那么 AB DE = ; BC EF
AB DE = ; AC DF BC EF = . AC DF
一般
特殊
L3
若将下图中的直线L2看成是平行于△ABC 的边BC的直线,那么可得: AD = AE .
AB AC
推论:平行于三角形一边的直线截其他两边 (或两边的延长线)所得的对应线段成比例.
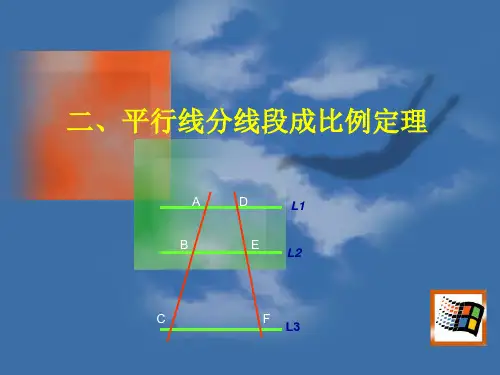
二、平行线分线段成比例定理
A D L1
B
E
L2
C
F
L3
平行线等分线段定理
A E D ? F
? B
图4
如果一组平行线在一条直线 上截得的线段相等,那么在其他直线上截得的线段也相等
A
E C ?F ? B
图5
C
推论1 经过梯形一腰的中点与底平行的 推论2
直线,必平分另一腰。
符号语言: ∵在梯形ABCD,AD∥EF∥BC,AE=EB ∴DF=FC
如果l1 // l2 // l3 ,
A B D E L1 L2 F D B C A E F L3 L1 L2 L3 C C D B (E) B A (D) E L1
且l , l ¢ 分别与 l1 , l2 , l3相交于 A, B, C , D, E , F .
L2
F A L3 L1 L2 F
一般
C
A
A B F D E C L1 L2 L3
D B
E C 图2
图1
四 课后小结
1、学习掌握平行线等分线段定理,了解定 理的证明。 2、正确理解“对应线段成比例”,能正确 写出需要的比例式。 3 了解平行线分线段成比例定理是一般情 况,平行线等分线段定理的特殊情况, 明确我们的研究是采用从特殊到一般的 数学方法。