当前位置：文档之家 › (完整版)正方形的判定方法.ppt

(完整版)正方形的判定方法.ppt

  • 格式：pdf
  • 大小：2.78 MB
  • 文档页数：20

下载文档原格式

  / 20

合集下载

1.3.2正方形的判定上课课件(北师大新版)

1.3.2正方形的判定上课课件(北师大新版)
[归纳总结] 对角线互相垂直的四边形的中点四边形是矩形．
数学的学习方法是严格、 严肃、严密——苏步青
平行四边形、矩形、菱形、正方形的判定小结
5种识 别方法
一个角是直角且一组邻边相等
学习反思
1、本节课我们学习了什么？
正方形的判定
1、定义法 2、矩形菱形法 3、对角线法
数学的学习方法是严格、 严肃、严密——苏步青
探究问题一
正方形的判定
数学的学习方法是严格、 严肃、严密——苏步青
重难互动探究 例1 [教材例2变式题] [2013· 铁岭] 如图1－3－21所 示，△ABC中，AB＝AC，AD是△ABC的角平分线， 点O为AB的中点，连接DO并延长到点E，使OE＝OD， 连接AE，BE. (1)求证：四边形AEBD是矩形； (2)当△ABC满足什么条件时， 矩形AEBD是正方形，并说明理由．
1）一组邻边相等的矩形是正方形
2、矩形菱形法：
2） 有一个角是直角的菱形是正方形
3、对角线法：
两条对角线互相垂直平分 且相等的四边形是正方形。
老师说下列三个图形都是正方形,你相信吗?
数学的学习方法是严格、 严肃、严密——苏步青
5 2 5 2
有一组邻边相等并且有一个 角是直角的平行四边形是正 方形。
矩形、等 腰梯形 菱形
菱形
正方形
中点四边形
矩形
正方形
数学的学习方法是严格、 严肃、严密——苏步青
例2在矩形ABCD中，BE平分∠ABC，CE平分∠DCB， BF∥CE，CF∥BE，求证：四边形BECF是正方形． 证明：∵BF∥CE，CF∥BE ∴四边形BECF是平行四边形， 又∵在矩形ABCD中，BE平分 ∠ABC，CE平分∠DCB ∴∠EBA=∠ECB=45° ∴∠BEC=90°，BE=CE ∴四边形BECF是正方形．

3.正方形的性质与判定第1课时正方形的性质PPT课件(北师大版)

3.正方形的性质与判定第1课时正方形的性质PPT课件(北师大版)

第一章
特殊平行四边形 3．正方形的性质与判定
第1课时 正方形的性质
第1课时 正方形的性质
1 …知…识…回…顾…. 2 …新…知…导…航…. 3 …轻…松…过…招….
第1课时 正方形的性质
知识回顾
正方是轴对称图形，它有 4 条对称轴，即经 过对边中点的直线或两对角线所在直线：正方形又 是中心对称图形，两对角线交点是它的对称中心 （也是对边中点的直线的交点）。 .
第1课时 正方形的性质
新知导航
变式训练
1.已知正方形ABCD的对角线相交于点O. （1）若周长为8，则对角线长为 2 2 ， 面积为 4 ； （2）图中共有 8 个等腰直角三角形．
第1课时 正方形的性质
新知导航
2.如图，过正方形ABCD的顶点B作直线l，过点A，C 作l的垂线，垂足分别为E，F，若 AE＝1，CF＝3.求AB的长．
第1课时 正方形的性质
轻松过招
3．如图，正方形ABCD中，E为CD边上一点，F为 BC延长线上一点，且CE＝CF. （1）求证：△BCE≌△DCF；
(1)证明：∵四边形ABCD是正方形，
∴BC＝DC，∠BCE＝∠DCF＝90°
CE＝CF
在△BCE和△DCF中， ∠BCE＝∠DCF ，
∴△BCE≌△DCF.
解：∵四边形ABCD是正方形， ∴∠CBF＋∠FBA＝90°，AB＝BC， ∵CF⊥BE，∴∠CBF＋∠BCF＝90°， ∴∠BCF＝∠ABE， ∵∠AEB＝∠BFC＝90°，AB＝BC， ∴△ABE≌△BCF(AAS)，∴AE＝BF＝1，BE＝CF＝3， ∴AB＝ AE2＋BE2 ＝ 1＋9 ＝ 10 .
第1课ห้องสมุดไป่ตู้ 正方形的性质
轻松过招

《认识正方形》PPT课件(2024)

《认识正方形》PPT课件(2024)

正方形特点
四边等长，四角均为90度。
2024/1/30
4
正方形与长方形关系
正方形是长方形的特例
当长方形的长和宽相等时，即为正方 形。
长方形与正方形的区别
长方形长和宽不等，而正方形四边等 长。
2024/1/30
5
正方形对称性
正方形的轴对称性
正方形有两条对称轴，分别是两条对角线。
正方形的中心对称性
正方形关于其中心点对称，即任意一点关于中心点的对称点仍在正方形上。
19
05
正方形相关数学问题探 讨
2024/1/30
20
正方形内角和问题
正方形内角和定理
正方形四个内角之和等于360度 。
证明方法
通过划分正方形为两个三角形， 利用三角形内角和定理进行证明
。
应用举例
解决与正方形内角相关的几何问 题，如角度计算、形状判断等。
2024/1/30
21
正方形对角线性质
2024/1/30
2024/1/30
11
03
正方形在生活中的应用
2024/1/30
12
建筑设计中应用
正方形作为建筑的基本形状之一，在建筑设计中广泛应用，如房屋、大厦、广场等 。
正方形的平面布局可以使得空间更加均衡、稳定，符合建筑美学的要求。
2024/1/30
正方形的建筑结构具有良好的承重性和稳定性，能够保证建筑的安全性和耐久性。
• 实例2：已知正方形周长为24m，求其边长和面积。 • 边长计算：a = C / 4 = 24m / 4 = 6m。 • 面积计算：S = a² = 6m × 6m = 36m²。 • 应用场景：正方形周长与面积计算在建筑设计、土地测量、

2024优质小班认识正方形ppt课件(2024)

2024优质小班认识正方形ppt课件(2024)

区域。
22
05 总结回顾与拓展 延伸
2024/1/30
23
关键知识点总结回顾
2024/1/30
正方形的定义和性质
正方形是四边相等、四个角都是直角的四边形，具有对称性、稳 定性等性质。
正方形的周长和面积计算
正方形的周长是其边长的四倍，面积是其边长的平方。
正方形的识别和应用
能够在生活中识别正方形，了解正方形在建筑设计、艺术创作等领 域的应用。
1 2
家具摆放
正方形家具摆放稳定，易于搭配，节省空间。
墙面装饰
正方形装饰画、照片墙等使墙面更加美观。
3
地面铺装
正方形地砖、地板等铺装材料易于施工，视觉效 果佳。
2024/1/30
20
手工制作中裁剪和拼接正方形材料
剪纸艺术
利用正方形纸张进行剪纸创作，可制作出各种精 美图案。
布艺制作
正方形布块易于裁剪和缝制，适合制作抱枕、桌 布等家居用品。
01
ቤተ መጻሕፍቲ ባይዱ02
03
练习题一
给定一个边长为5厘米的 正方形，计算其周长和面 积。
2024/1/30
练习题二
一个正方形地块的边长为 20米，计算该地块的面积 。
练习题三
一个正方形画布的边长为 1.5米，计算该画布的周长 。
12
03 绘制和识别正方 形图形技巧
2024/1/30
13
绘制标准正方形步骤示范
准备工具
计算正方形地块的面积，如地砖、画布等；计算正方形物体的表面积，如魔方的一个面。
2024/1/30
10
单位换算技巧与注意事项
单位换算技巧
掌握常见的长度单位换算关系，如1米=100厘米，1厘米=10 毫米等。

18.2.3正方形 正方形的判定(教学课件)-人教版数学八年级下册

18.2.3正方形 正方形的判定(教学课件)-人教版数学八年级下册

探究点
正方形的判定
归纳总结：
（1）四条边相等、四个角都是直角的四边形是正方形 从四边形出发
（2）对角线互相垂直平分且相等的四边形是正方形 （1）有一组邻边相等并且有一个角是直角的平行四边 从平行四边形 形是正方形 出发 （2）对角线互相垂直且相等的平行四边形是正方形 从矩形出发 对角线互相垂直的矩形是正方形 从菱形出发 对角线相等的菱形是正方形
A
D
∴AB=BC=CD=DA，∠A=∠C,∠B=∠D.
又∠A=90°,
ቤተ መጻሕፍቲ ባይዱ
B
C
∴易得∠A=∠B=∠C=∠D=90°.
∴四边形ABCD是正方形.
归纳总结：有一个角是直角的菱形是正方形
探究点
正方形的判定
在上面的证明过程中,是分别从矩形、菱形出 发,添加边或角的条件后得到正方形,那么还有没 有通过添加边、角、对角线的条件可以得到其他 判定正方形的方法呢? 大家想一想．
课堂总结
知识结构
四边形
平行四边形
正 矩形 方 菱形
形
课堂总结
知识结构
课堂总结
1. 教材P62习题18.2第13题.
课后作业
1. 如图，E,F,M,N 分别是正方形ABCD四条边上的
点，且AE=BF=CM=DN,试判断四边形EFMN是什么
图形，并证明你的结论. 【选自教材P62，习题18.2第13题】
把能活动的菱形木框的一个角变为直角(如图),
能否得到正方形?
探究点
正方形的判定
2. 有一个角是直角的菱形是正方形
正方形
可以看到,这个变化过程中只要改变菱形的一 个角,就能得到正方形．
下面我们进行证明:
探究点

新北师大版初三上册数学(九年级) 第一章：3、《正方形的判定》课件

新北师大版初三上册数学(九年级) 第一章：3、《正方形的判定》课件
解： ∵ DE∥AC，DF∥AB
∴ 四边形AEDF是平行四边形
（2）当满足什么条件时，四边形AEDF是矩形？
解： ∵ 一个角为直角的平行四边形为矩形∴ ∠BAC90°时，四边形AEDF是矩形
[趁热打铁]
（3）当满足什么条件时，四边形AEDF是菱形？ 解：∵ 有一组邻边相等的平行四边形是菱形
∴ 当AD平分∠BAC时，四边形AEDF是菱形
质 对角线
每条对角线平分一组对角
[实践出真知]
做一做：将矩形纸片对折两次，怎样裁剪才能使剪下的三角形 展开后是个正方形？
（1）
（2）
剪口与折痕成 45°角
（3）
（4）
[实践出真知]
问题2：满足怎样条件的矩形是正方形？
矩形
一组邻边相等 或对角线互相垂直
正方形
问题3：满足怎样条件的菱形是正方形？
菱形
亲爱的读者： 2、千世里上之没行有，绝始望于的足处下境。，只20有20对年处7月境1绝2日望星的期人日。二〇二〇年七月十二日2020年7月12日星期日 春去春又回，新桃换旧符。在那桃花盛开的地方，在 3、少成年功易都学永老远难不成会，言一弃寸，光放阴弃不者可永轻远。不。会成09功:01。7.12.202009:017.12.202009:0109:01:457.12.202009:017.12.2020
1.3.2 正方形的判定
[温故而知新]
1.在平行四边形的基础上对矩形、菱形的判定 矩形
平行四边形
菱形
[温故而知新]
2.正方形的定义及性质
正方形 有一个角是直角且一组邻边相等的平行四边形叫做
平行四边形
一个角是直角 且一组邻边相等
正方形
边
正方形的对边平行且相等

正方形的判定PPT教学课件

正方形的判定PPT教学课件
最先开辟新航路，进行殖民扩张和掠夺，实力强大。
衰落：
1588年，西班牙的“无敌舰队”被英国打败，从此丧失 海上霸主地位。
原因：葡萄牙人和西班牙人获得的大量财富，在欧洲大量采
购商品，金银流入欧洲其他国家，没有在本国转化为资本原 始积累。
新航路开辟后,贸易中心发生了哪些变化? 由地中海转移到大西洋沿岸
• 如图，在Rt△ABC中，∠ACB=90°,CD平 分∠ACB，DE⊥AC，DF⊥BC，垂足分别 为E、F，试说明四边形DECF是正方形.
A
E
D
C
F
B
合作交流
• 如图，在△ABC中，AB＝AC，D是BC的中 点，DE⊥AB，DF⊥AC，垂足分别为E、F.
• (1)求证：DE＝DF；
• (2)只添加一个条件:
（3）资本主义原始积累的过程是一个血腥的掠夺过程， 资本主义的每一步发展都同残酷的殖民掠夺密不可分。
问答题： 英国世界殖民霸权地位是怎样确立的？
1588年，英国打败了西班牙的“无敌舰队”，开始树立海上霸权
17世纪，英国在印度和北美建立殖民地。
17世纪下半期，英国通过三次英荷战争打败了欧洲强国荷兰， 夺取了荷兰在北美的殖民地新尼德兰，荷兰从此丧失了海上 殖民强国的地位。
洲 “ 换
口 载 上
出 程
取 ” 奴 隶
廉 货 物 到 非
从 欧 洲 港
非洲
三、世界市场的拓展
伴随着殖民活动的进行，世界市场体系进一 步形成。在这一过程中，殖民主义有哪些 罪恶？（早期殖民扩张形式） 垄断贸易 抢掠财物 灭绝种族 贩卖黑奴
评价殖历史民活主动的义基的本标后准果、方法 是否推动历史的进步 一分为二、分清主次
初中数学九年级 上册

正方形的判定定理(课堂PPT)

正方形的判定定理(课堂PPT)

A
D/ D
从
证题思路分析
条
A/
件 ①.由已知正方形证三角形全等；
C/
分 析பைடு நூலகம்
②.证得菱形； ③.再证直角； ④.是正方形
B B/
C
20
已知:正方形ABCD中,点E、F、G 、H分别是 AB 、BC 、CD 、DA的中点,试判断四边形 EFGH是正方形吗?为什么?
证明:
∵四边形ABCD是矩形,
∴∠ABC=900,四边形ABCD是平行四边形.
∵AC⊥BD,
A
D
∴四边形ABCD是菱形.
O
∵∠ABC=900.
∴四边形ABCD是正方形.
B
C
8
正方形的判定方法5
对角线相等的菱形是正方形.
已知:四边形ABCD是菱形,且对角线AC=BD. 求证:四边形ABCD是正方形.
∵四边形ABCD是菱形,∠A=900,
∴AB=BC,∠C=∠A=900,∠B=1800-∠A=900.
∴∠A=∠B=∠C=900. ∴四边形ABCD是矩形. ∵AB=BC, ∴四边形ABCD是正方形.
A
D
B
7C
正方形的判定方法4
对角线互相垂直的矩形是正方形.
已知:四边形ABCD是矩形,且AC⊥BD. 求证:四边形ABCD是正方形.
∴ DE=DF( 角平分线上的点到角两边的距离相等的定理 )
∴四边形ABCD是正方形（ 有一组邻边相等的矩形是正方形) 16
5、如图，在Rt△ABC中，∠C=900，∠A、∠B的角平分 线相交于点D，DE⊥BC于点E，DF⊥AC于点F， 求证：四边形CEDF是正方形。
证明：过点D作DG⊥AB，垂足为G

3.正方形的性质与判定第2课时 正方形的判定PPT课件(北师大版)

3.正方形的性质与判定第2课时 正方形的判定PPT课件(北师大版)
证明：∵DE⊥BC，DF⊥AC，∠ACB＝90° ∴∠CFD＝∠DEC＝∠FCE＝90° ∴四边形CFDE是矩形 又∵CD平分∠ACB，DF⊥AC，DE⊥BC ∴DF＝DE，∴矩形CFD松过招
第二招
3．在△ABC中，AB＝AC，∠A＝90°，D、E、F分 别是BC、AB、AC边上的中点． 求证：四边形AEDF是正方形．
第2课时 正方形的判定
新知导航
知识点3：四边相等且有1个角是直角 【例3】已知，如图，在△ABC中，∠ACB＝90°，CD是∠ACB 的平分线，CD的垂直平分线分别交AC，CD，BC于点E，O，F. 求证：四边形CEDF是正方形．
证明：∵CD的垂直平分线分别交AC，CD， BC于点E，O，F，∴EC＝ED，FC＝FD， ∵∠ACB＝90°，CD平分∠ACB， ∴∠ACD＝∠BCD＝45°，又CD⊥EF ∴△CEF为等腰直角三角形，∴CE＝CF ∴ED＝EC＝CF＝FD，∴四边形CEDF为菱形， ∵∠ACB＝90°，∴四边形CEDF为正方形．
证明：如图，过点D作DN⊥AB于点N， ∵∠C＝90°，DE⊥BC于点E，DF⊥AC于点F， ∴∠C＝∠DEC＝∠DFC＝90°，∴四边形CFDE是矩形， ∵∠A、∠B的平分线交于点D，DE⊥BC于点E，DF⊥AC于 点F，DN⊥AB于点N， ∴DE＝DN，DN＝DF，∴DF＝DE， ∴矩形CFDE是正方形．
证明：∵D，E，F分别是BC，
AB，AC的中点．∴AE∥DF，DE∥AF
∵∠BAC＝90°，∴四边形AEDF是矩形
∵D，E，F分别是BC，AB，AC的中点
∴DE＝12
AC，DF＝
1 2
AB
又AB＝AC，∴DE＝DF.∴矩形AEDF是正方形．
第2课时 正方形的判定

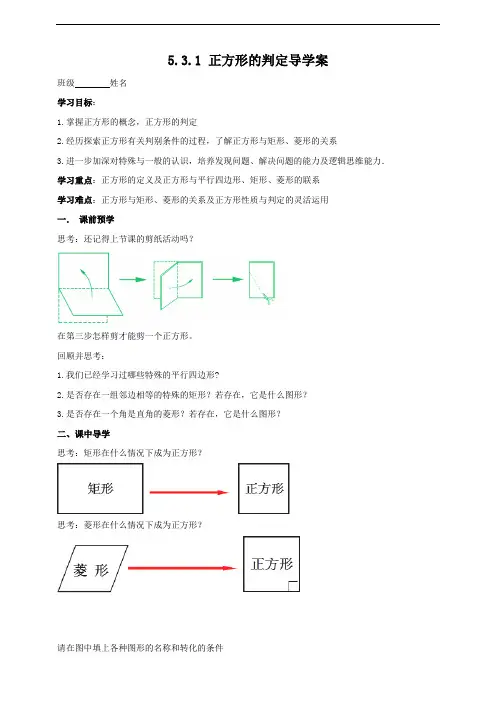
正方形的判定 （27张PPT）学案

正方形的判定 （27张PPT）学案

5.3.1 正方形的判定导学案班级姓名学习目标：1.掌握正方形的概念，正方形的判定2.经历探索正方形有关判别条件的过程，了解正方形与矩形、菱形的关系3.进一步加深对特殊与一般的认识，培养发现问题、解决问题的能力及逻辑思维能力．学习重点：正方形的定义及正方形与平行四边形、矩形、菱形的联系学习难点：正方形与矩形、菱形的关系及正方形性质与判定的灵活运用一．课前预学思考：还记得上节课的剪纸活动吗？在第三步怎样剪才能剪一个正方形。

回顾并思考：1.我们已经学习过哪些特殊的平行四边形?2.是否存在一组邻边相等的特殊的矩形？若存在，它是什么图形？3.是否存在一个角是直角的菱形？若存在，它是什么图形？二、课中导学思考：矩形在什么情况下成为正方形？思考：菱形在什么情况下成为正方形？请在图中填上各种图形的名称和转化的条件正方形定义：______________________________________________________________正方形是特殊的平行四边形，也是特殊的矩形，也是特殊的菱形。

你能得到哪些判定定理？(1)直接用正方形的定义判定，即先判定一个四边形是平行四边形，若这个平行四边形有一个角是直角，并且有一组邻边相等，那么就可以判定这个平行四边形是正方形；______________________________________________________________(2)先判定一个四边形是矩形，再判定这个矩形是菱形，那么这个四边形是正方形；______________________________________________________________(3)先判定四边形是菱形，再判定这个菱形是矩形，那么这个四边形是正方形.__________________________________________________________拓展延伸上述三种判定条件是判定四边形是正方形的一般方法，可当作判定定理用，但由于判定平行四边形、矩形、菱形的方法各异，所给出的条件各不相同，所以判定一个四边形是不是正方形的具体条件也相应可作变化，在应用时要仔细辨别后才可以作出判断.做一做(1)正方形的一条对角线把正方形分成两个全等的等腰直角三角形（）(2)对角线互相垂直且相等的四边形是正方形（）(3)如果一个菱形的对角线相等，那么它一定是正方形（）(4)如果一个矩形的对角线互相垂直，那么它一定是正方形（）(5)四条边相等，且有一个角是直角的四边形是正方形（）例1 已知：如图，在Rt△ABC中，∠ACB=90°，CD是∠ACB的平分线，DE⊥BC，DF⊥AC，垂足分别是E，F.求证：四边形CFDE是正方形．三、课后延学1.如图，每个小正方形的边长为1，A、B、C是小正方形的顶点，则∠ABC的度数为() A．90° B．60° C．45° D．30°2.如图，边长为(m＋3)的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是()A．2m＋3B．2m＋6C．m＋3D．m＋63.如图，AC、BD是矩形ABCD的对角线，过点D作DE∥AC交BC的延长线于E，则图中与△ABC全等的三角形共有()A．1个 B．2个 C．3个 D．4个4.如图，已知矩形ABCD沿对角线BD折叠，记点C的对应点为C′，若∠ADC′＝20°，则∠BDC的度数为________．5.在平面内正方形ABCD和正方形CEFH如图放置，连接DE，BH两线交于点M.求证：(1)BH＝DE；(2)BH⊥DE.6.（2019•黄石）如图，在平面直角坐标系中，边长为2的正方形ABCD的边AB在x轴上，AB边的中点是坐标原点O，将正方形绕点C按逆时针方向旋转90°后，点B的对应点B'的坐标是（）A．（-1，2）B．（1，4） C．（3，2） D．（-1，0）7.（2019•河池）如图，在正方形ABCD中，点E，F分别在BC，CD上，BE=CF，则图中与∠AEB相等的角的个数是（）A．1 B．2 C．3 D．4答案：1.C2.A3.D4.55°5.证明：(1)在正方形ABCD与正方形CEFH中，BC＝CD，CE＝CH，∠BCD＝∠ECH＝90°，∴∠BCD＋∠DCH＝∠ECH＋∠DCH，即∠BCH＝∠DCE，∴△BCH≌△DCE，∴BH＝DE(2)由(1)得，∠CBH＝∠CDE，∴∠DMB＝∠BCD＝90°，∴BH⊥DE6.C7.C。

正方形(2)——判定 —初中数学课件PPT

正方形(2)——判定 —初中数学课件PPT
第十八章 平行四边形
第26ห้องสมุดไป่ตู้时 正方形（2）——判定
课前学习任务单
任务一：明确本课时学习目标 1.掌握正方形的判定方法. 目标 2.能够综合运用正方形的性质和判定解决相关问题.
任务二：复习回顾
1.矩形和菱形的判定方法有哪些？请从边、角、对角线
的角度分别说明.__略___._________________________；
知识点3：正方形判定的综合运用
【例3】已知：如图18-26-4
ABCD中，O是CD的中点，连
接AO并延长，交BC的延长线于点E．
（1）求证：△AOD≌△EOC；
（1）证明：∵四边形ABCD是平行四边形， ∴AD∥BC．∴∠D=∠OCE，∠DAO=∠E． ∵O是CD的中点，∴OC=OD. 在△AOD和△EOC中，
（2）∵∠ADB=90°，∠A=45°， ∴∠A=∠ABD=45°. ∴AD=BD. ∵E为AB的中点， ∴DE⊥AB，即∠DEB=90°. ∵四边形DEBF是菱形， ∴四边形DEBF是正方形.
9. 如图18-26-9，在△ABC中，∠C=90°，D为边BC上一点，E 为边AB的中点，过点A作AF∥BC，交DE的延长线于点F，连接 BF．（1）求证：四边形ADBF是平行四边形；
证明：（1）∵AF∥BC，∴∠AFE=∠BDE. 在△AEF与△BED中，
∴△AEF≌△BED（AAS）. ∴AF=BD. ∵AF∥BD， ∴四边形ADBF是平行四边形.
（2）当D为边BC的中点，且BC=2AC时，求证：四边形ACDF为
正方形． （2）∵CD=DB，AE=BE， ∴DE∥AC.∴∠FDB=∠C=90°. ∵AF∥BC， ∴∠AFD=∠FDB=90°.∴∠C=∠CDF=∠AFD=90°. ∴四边形ACDF是矩形. ∵BC=2AC，CD=BD，∴CA=CD. ∴矩形ACDF是正方形．

1.3.2正方形的判定 课件(共19张PPT)

1.3.2正方形的判定 课件(共19张PPT)
的中点.求证:四边形 EFGH 为菱形.
证明:∵四边形 ABCD 为矩形,∴AB
DC,AD
BC,∠B=∠A.
又∵E,F,G,H 分别为AB,BC,CD,AD的中点,

∴AH=BF= AD,AE=BE.∴△AEH≌△BEF,

∴EH=EF.同理,EH=HG,HG=FG,∴EH=EF=FG=HG,
∴四边形EFGH为菱形.
第2课时
正方形的判定
1.通过阅读课本，掌握正方形的判定定理，会运用平行四边形、矩
形、菱形、正方形的判定方法进行有关的证明和计算，发展学生
演绎推理的能力.
2.经历探究正方形的判定定理的过程，发展学生主动探究的学习习
惯、综合推理的能力，逐步掌握说理的基本方法，培养积极探索、
勇于创新的精神，以及推陈出新的创新能力.
∵AC⊥EF,∴四边形AECF是菱形.∵AE⊥AF,∴∠EAF=90°,
∴四边形 AECF是正方形.
典例精讲 【题型三】根据正方形的性质与判定求线段的长度
例5: 如图,在矩形纸片 ABCD 中,AB=6cm,BC=9cm.现将其沿 AE
折叠,使得点 B落在边AD 上的点 F 处,折痕与边 BC 交于点 E,则
对角线相等的菱形是正方形)
小组讨论（4min）
①猜想:菱形的中点四边形会是什么形状?（菱形的中点四边形是矩形）
②猜想:矩形的中点四边形会是什么形状?（矩形的中点四边形是菱形）
请尝试证明这两个猜想.
【证明 】①已知：如图①，四边形ABCD是菱形,点 E,F,G,H分
别是 AB,BC,CD,AD的中点.求证：四边形 EFGH为矩形.
(3)若原四边形的对角线垂直且相等，则新四边形是正方形.

《正方形的性质与判定》特殊平行四边形PPT(第1课时)教学课件

《正方形的性质与判定》特殊平行四边形PPT(第1课时)教学课件

再由一个直角，得出是矩形；最后由一组邻边相等可
F
得正方形；
证明: ∵ BF∥CE,CF∥BE，
∴四边形BECF是平行四边形. ∵四边形ABCD是矩形, ∴ ∠ABC = 90°, ∠DCB = 90°, ∵BE平分∠ABC, CE平分∠ DCB, ∴∠EBC = 45°, ∠ECB = 45°, ∴ ∠ EBC =∠ ECB .
第一章 特殊平行四边形
正方形的性质与判定
第1课时
导入新课
讲授新课
当堂练习
课堂小结
学习目标 1.了解正方形的定义及其与平行四边形的关系. 2.探索并证明正方形的性质定理.（重点） 3.应用正方形的性质定理解决相关问题.（难点）
导入新课
活动:观察这些图片，你什么发现？正方形四条边有什么关系？ 四个角呢？
A M
B
P
D
N C
∴∠ADB=∠CDB=45°.
∴∠MPD=∠NPD=45°.
∴DM=PM,DN=PN.
∴四边形NPMD是矩形（有一组邻边相等的矩形是正方形）.
课堂小结
矩形
平行四边形
一组邻边相等且一个内角为直角 （或对角线互相垂直平分且相等）
菱形
正方形
请同学们动手完成以上证明？
A
D
O
B
C
提示：可以先通过证明来得到正方形是矩形、菱形，然后利用矩形和菱形 的定理来完成该题.
想一想： 正方形是矩形吗？是菱形吗？
矩形 正方形 菱形 平行四边形
归纳 正方形是特殊的平行四边形,也是特殊的矩形,也是特殊的菱形.所 以平行四边形、矩形、菱形有的性质,正方形都有.
一 正方形判定的定理
动一动：过点A作射线AM的垂线AN,分别在AM , AN上取点B , D ,使
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。