矢量图解法

矢量图解法
矢量图解法的主要内容是：一个简谐量可以用一个矢量（称为旋转矢量）来表示，矢量的合成可以代替简谐量的加减。

从直角坐标系的原点作一矢量，令其长度等于交流电流的幅值。

在时刻，矢量与轴的夹角等于交流电流的初位相。

现使矢量以角速度沿逆时针方向匀角速的转动，这一矢量称为旋转矢量，它是由简谐量的三要素决定。

在任意时刻，旋转矢量与轴的夹角为，它在轴上的投影就是交流电流在该时刻的瞬时值
由于矢量间的相对位置不变，因此可以用矢量合成的方法来求简谐量的加减。

矢量图解法可用于串联、并联或混联交流电路的计算。

用矢量图解法求解交流电路首先要确定参考矢量。

若电路是串联电路，由于通过各元件的电流相同，一般选电流为参考矢量，使之沿
轴方向，再根据各元件上的电压与电流的位相关系，画出各电压的矢量，然后进行矢量合成。

若电路是并联电路，由于通过各元件的电压相同，一般选电压为参考矢量，再根据各元件上的电流与电压的位相关系画出各电流的矢量，然后进行矢量合成。

矢量图解法简介在图像处理和图形设计领域，矢量图是一种基于数学公式描述的图像类型。

与位图图像不同，矢量图使用数学对象（如线段、多边形、曲线等）来表示图像的形状和颜色，而非以像素表示。

矢量图的主要优势是可以无损地进行缩放和变形，并且具有较小的文件大小。

由于矢量图使用数学对象而非位图存储图像数据，因此矢量图也可以更容易地进行编辑和修改。

本文将介绍矢量图解法的基本原理和常见应用场景，并探讨矢量图在图像处理和图形设计中的优势和局限性。

矢量图的工作原理矢量图使用数学公式来描述图像的形状和颜色。

图像中的每个元素（如线段、多边形、曲线等）都由数学方程式定义。

矢量图使用向量和曲线来表示形状。

通过定义始点坐标、终点坐标、绘图方向和曲线类型等参数，可以精确地绘制出各种形状。

矢量图中的颜色通常由渐变、填充和描边等技术实现。

渐变使用数学方程式定义色彩的渐变过程，填充使用颜色或纹理填充形状的内部，而描边则用于形状的边缘。

矢量图可以保存为各种文件格式，如SVG（可缩放矢量图形）、AI（Adobe Illustrator）、EPS（Encapsulated PostScript）等。

矢量图的优势和应用场景1. 缩放和变形无损矢量图可以无损地进行缩放和变形，因为图像的形状是基于数学公式计算得出的。

与位图图像不同，无论对矢量图进行多大或多小的缩放，都不会导致图像的质量损失。

这使得矢量图在需要频繁调整大小的设计和印刷制作中非常有用。

2. 文件大小小由于矢量图使用数学公式来描述图像，矢量图文件通常比位图图像文件更小。

这使得矢量图在需要在网络上进行传输或嵌入到其他文档中时非常方便。

3. 可编辑性强矢量图具有良好的可编辑性，可以方便地修改和调整图像的各个元素。

通过编辑软件，可以添加、删除、变换和调整矢量图的各个部分，使得图形设计和图像处理更加灵活和高效。

4. 特效和过渡效果矢量图可以通过使用渐变、透明度、阴影等技术实现各种特效和过渡效果。

12、矢量图解法
请你多多关注，学习少走弯路，成绩突飞猛进，高考考题全对！巧学迷津
矢量图解法就是通过作矢量图来分析或求解某个物理量的大小及变化趋势的一种解题方法.通过作矢量图来揭示物理过程、物理规律，具有直观形象、简单明了等优点. 特别是对受三力（一个力是恒力，第二个力的方向恒定，）作用而平衡的物体，将力矢量图平移使三力组成一个首尾依次相接的封闭力三角形，矢量图解法在处理动态平衡问题时方便、直观，容易定性判断和分析，也可定性计算，灵活应用作图法会给解题带来很大方便.
调研讲解
巧学巧练
此文取材于快速提高物理成绩的奇书——《巧学妙解王高中物理》一书，不怕物理学不会，就怕不用妙解王，此书内容会陆续推出，百度书名即行！。

矢量图解法在边坡稳定性评价中的应用李明连摘要：控制岩质边坡稳定性的主要因素，是岩体的结构面。

岩质边坡的稳定性评价，通常是通过分析结构面与坡面的关系进行的。

在极坐标上坡面和结构面都可用矢量表示，结构面矢量与坡面矢量之间夾角和模的大小能准确反映两者之间的关系。

文章从这一点出发提出了一种评价边坡稳定性的新方法。

关键词：结构面；坡面；矢量图Abstract: The chief factor to dominate the stability of rock slope is structural planes in the rock . Generally, the evalution of stability of the rock slope is to analyze by the relationship between the structural planes in the rock and the plane of slope . Both the plane of the slope and the structural plane in the rock may be showed by vector with polar coordinates .The relationship between the structural plane and the plane of the slope can be reflected exactly with their vector. A new method to evaluate the stability of the slope based on the pricpiple was discussed in the paper. Key words: structural plane; plane of slope; vectorgraph1 前言一般说来，岩体的结构面（含结构面交线，以下同）是控制岩质边坡稳定性的主要因素，而平面滑动和楔形滑落、倾倒、剥落又是岩质边坡破坏的主要模式。

§2 矢量图解法矢量图解法的步骤是：（1）先定适当的比例尺，用某一带箭头的线段代表一个矢量的大小和方向，作出矢量图。

（2）按“平行四边形法则”或按“多边形法则“对矢量进行相加或相减。

（见矢量运算部分）（3）依据选定的比例尺，从图中直接量出合矢量的大小并确定其方向。

例4－6作用于一点上的三个力同在一平面内，其大小F 1＝FeBr2＝10N ，F 3＝15N ，它们与x 轴的夹角分别为300、600、及－450（图4－10所示）。

求合力F 的大小和方向。

解：以水平方向为x 轴，选取比例线段，作力矢量多边形OABC （图4－11）。

按比例量得F ＝24.5N ，F 与x 轴的正向的夹角为α＝9010/。

例4－7 水流向东，速率为2km/h ，汽船以8km/h 的航速在向东偏北600的方向航行。

一位旅客在甲板上散步，速度为1km/h ，面向正西北。

求旅客对岸的速度。

解：依据速度合成规律，有：V V V V 人对岸人对船船对水水对岸＝＋＋令X 轴的正向向东，Y 轴的正向指北，选取比例线段，作速度矢量多边形OABC （图4－12）从速度矢量多边形中量出OC 的长度和角度θ得：09.2km/h,=55V θ人对岸＝所以，旅客对岸的速率是9.2km/h ，方向向东偏北550。

例4－8某人以4km/h 的速率向正东方向前进时，感觉风从正北方向吹来，若将速率增一倍，则感觉风从东北方向吹来。

求风速和风向。

解：依题意作速度矢量图（图4－13所示），由图可得：/)V km h =，风向F 1F 2 F 3－450300 300 xo 图 4-10C图4－11V 东从西北吹来。

（作图原理请读者自行分析）V V V 风对人风对地人对地＝＋， 同理：///V V V 风对人风对地人对地＝＋例4－9某人上抛出一球，1秒后仍斜向上升，飞行方向与水平方向成450角，速度为20m/s 。

(g=10m/s 2) 求：（1）3秒末球的速度的大小和方向；（2）抛出时球的速度大小和方向。

正交分解法和矢量图解法正交分解法和矢量图解法是解决力学问题最基本的解法，我们以教材第三章课后复习与提高B 组习题第4题为例，谈谈这两种解法的基本思路，希望对同学们有所帮助。

题目如下：如图1所示，重力为G 的木块，恰好能沿倾角为θ的斜面匀速下滑，那么要将木块沿斜面匀速向上推，必须加多大的水平推力F?1. 正交分解法题上共涉及两个过程，前者木块匀速下滑，后者木块被匀速向上推。

先看第一个过程，物体受重力、弹力和摩擦力三个力的作用，如图2所示，因为物体匀速下滑，所以合外力为0，也可以理解为，其中任何两个力的合力跟第三个力是一对平衡力，我们作支持力F N 和摩擦力F f 的合力Q ，Q 与重力是一对平衡力，即：Q=mg ，如图3所示，其中，支持力F N 和竖直方向间的夹角为θ。

由图可知：θcos θcos mg Q F N ==θsin θsin mg Q F f ==，又因图 1图 3图 2为木块和斜面间的滑动摩擦力F f 等于压力F N 乘以摩擦系数μ，所以有：θtan θcos θsin μ===mg mg F F Nf 。

再研究木块被水平恒力F 推着匀速向上运动的过程，此时木块受四个力的作用，如图4所示。

我们以木块的重心为原点，沿斜面向上为X 轴正向，垂直于斜面向上为Y 轴正向，建立平面直角坐标系，将物体所受的每一个力都沿两坐标轴的方向进行分解，如图5所示，其中，水平推力F 与斜面间的夹角为θ，有：θcos F F x =，θsin F F y -=；0='Nx F ，N Ny F F '='；θsin mg G x -=，θcos mg G y -=；f fxF F '-='，0='fy F 。

因为木块匀速向上运动，所以合外力为0，X 方向分量式为：0=+'+'+x fx Nx xG F F F ，即：0θsin 0cos θ=-'-+mg F F f ；Y 轴方向分量式为：0=++'+'y y fy NyF G F F ，即：0θsin θcos 0=--+'F mg F N 。

矢量图解法光栅衍射
光栅衍射是一种物理性现象，是指当光束穿过带有一组正交栅格阵列时，光线就会产生衍射而有明显的图案，这一现象被称为“光栅衍射”。

光栅衍射的机理和全反射有很多相似之处，只不过前者的低角度透过样板中的栅格而造成的偏振特性有效的结果是多普勒衍射而强烈的图案，而后者则是在均匀材料中，全体反射而成的穿透图案。

在实验室应用中，光栅衍射通常被用来测量粒子的大小。

使用光栅衍射，利用粒子在栅格阵列中受衍射而衍生出来的图案来测定粒子的直径，其原理是粒子大小和衍射图案之间存在一定的统一比例关系。

由于光栅衍射可以满足粒子粒径检测的要求，它已经成为粒子径向分布的重要技术手段。

此外，矢量图解法也可以用来分析光栅衍射的图案，它采用矢量图的方式，对光栅衍射图案进行分析。

针对具体环境，矢量图解法根据图形拆解各个特征，捕捉-衍射位置，分析-直径，甚至可以从图案中提取衍射角度，构建-介电常数以及拓扑索引。

总之，光栅衍射既可以用于表征粒子粒径测量，也可以用矢量图解法来精确分析图案，为图形建模和材料常数测定提供精确的数据和强有力的支持。

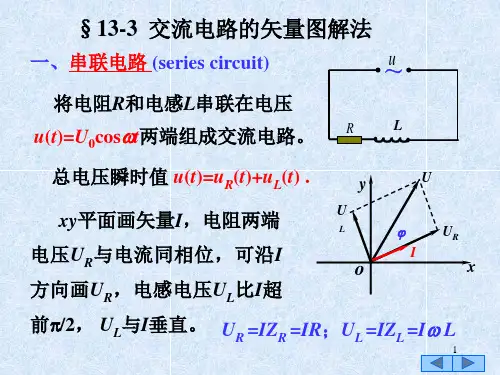
§3. 元件的串联、并联 矢量图解法 p338根据交流元件的联结形式不同，也将交流电路区分为简单交流电路与复杂交流电路。

类似于直流电路，元件最简单的联结方式为串联和并联，而凡是能够通过运用元件串、并联的计算法将电路化为一个单回路的交流电路称为简单交流电路；反之，不能将交流元件的联结方式归并为串、并联的电路，称为复杂交流电路。

同频交流简谐量的叠加 p394 5-38、40、43这里讨论的是由简谐交流电源与集中元件联结而成的线性的简单交流电路，在似稳条件下，整个电路满足电流连续性方程，且能够引进电压的概念，因此，与直流电路中电阻的串、并联一样，交流串、并联电路中，元件上的交流电压、电流在任意时刻的瞬时值之间的关系也比较简单。

以图示的两个元件的串、并联电路为例，串联电路中，通过各元件的电流的瞬时值处处相等，电路两端的电压瞬时值等于各元件上分压瞬时值之和,有)()()(21t i t i t i ==， )()()(21t u t u t u +=；因此求电路中总电压的瞬时值将归结为求两个同频简谐量的叠加。

设：)cos()(10101ϕω+=t U t u ，)cos()(20202ϕω+=t U t u 则总电压为)cos()cos()()()(2020101021ϕωϕω+++=+=t U t U t u t u t u 利用三角函数和差化积公式，可得叠加结果仍为同频简谐量，即)cos()(00ϕω+=t U t u总电压峰值及其初相位为 ,)cos(2102020102202100ϕϕ−++=U U U U U202010102020101010cos cos sin sin tan ϕϕϕϕϕU U U U ++=− 可见，两分电压的初相差出现在总电压的峰值表达式中，电路总电压峰值（或有效值）一般不等于分电压的峰值（或有效值）之和，20100U U U +≠ 或 21U U U +≠对于并联电路,各元件两端的电压瞬时值是共同的，而总电流瞬时值等于各元件上分电流瞬时值之和，有 )()()(21t u t u t u ==，)()()(21t i t i t i +=同样，电路总电流峰值（或有效值）一般也不等于分电压的峰值（或有效值）之和，有20100I I I +≠ 或 21I I I +≠如何解决峰值和有效值的叠加问题？两种简便方法一．矢量图解法 用旋转矢量U 在x 轴上的分量代替简谐量总电压为)cos()cos()()()(2020101021ϕωϕω+++=+=t U t U t u t u t u,)cos(2102020102202100ϕϕ−++=U U U U U202010102020101010cos cos sin sin tan ϕϕϕϕϕU U U U ++=−（一） 串联电路1． R、C 串联*电流： *电压：)()()(t i t i t i c R == )()()(t u t u t u c R += ↓ ↓ ↓ ↓ ↓ ↓ c R I I == c R U U U += *矢量长度：可以对应峰 值，也可以对应有效值，有效值与峰值的关系为2200I I U U == *画图：依据R、L、C 上电压与电流的相位关系*计算 CR Z Z U U C I IZ U IR U R c R c c c R ωω1,,=====2222221 +=+=+=C R I Z R I U U U C R C ω 221 +==C R I U Z ω CR U U R C ωϕ1tan tan 11−−== 表明：1）c R U U U +≠；2）分电压有效值的分配与各元件的阻抗成正比。

力的合成与分解力是物体相互作用的结果，它可以描述物体的运动状态以及受力的效果。

在物理学中，我们经常需要研究多个力对物体的综合作用，这就需要运用力的合成与分解的方法。

力的合成是指将多个力合并成一个等效的力，而力的分解则是将一个力分解为多个分力的过程。

一、力的合成力的合成是指将多个力合并成一个等效的力，常用的方法有矢量图解法以及三角函数法。

1. 矢量图解法矢量图解法是通过在力的作用点上按比例绘制各个力的矢量，然后将它们首尾相连，形成合力的合成矢量。

具体步骤如下：步骤一：在力的作用点处画出各个力的矢量，矢量的长度代表力的大小，矢量的方向代表力的方向。

步骤二：将各个力的矢量首尾相连，形成一个多边形。

步骤三：连接多边形的起点和终点，得到合力的合成矢量。

2. 三角函数法三角函数法是利用三角函数的性质计算合力的大小和方向。

具体步骤如下：步骤一：将各个力按照坐标轴方向分解成水平方向和垂直方向的分力。

步骤二：计算各个分力的代数和，得到水平方向和垂直方向的合力。

步骤三：利用三角函数求解合力的大小和方向。

二、力的分解力的分解是指将一个力分解为多个分力的过程，常用的方法有正余弦分解法、平行四边形法等。

1. 正余弦分解法正余弦分解法是将一个力分解为水平方向和垂直方向的分力。

具体步骤如下：步骤一：在力的作用点处，假设一个与力方向垂直的坐标轴。

步骤二：根据角度的定义，利用正弦函数和余弦函数求解力在水平方向和垂直方向上的分力。

2. 平行四边形法平行四边形法是将一个力分解为两个互相垂直的力。

具体步骤如下：步骤一：在力的作用点处，通过画一个平行四边形将力进行分解。

步骤二：根据平行四边形的性质，可以得到两个互相垂直的力。

三、实例应用力的合成与分解在物理学中有广泛的应用。

例如，在斜坡上有一个物体受到重力和斜坡面的支持力，我们可以通过合成这两个力来求解物体在斜坡上的运动情况。

又比如，当一个船要靠岸时，需要考虑风力和潮流对船的影响，我们可以将风力和潮流的力合成为一个等效力，以便进行船只的控制和导航。