下载文档原格式
板弯曲荷载计算公式在工程设计中，板材的弯曲荷载计算是非常重要的一项工作。
通过计算板材的弯曲荷载，可以确定板材的受力情况，从而保证工程的安全性和稳定性。
本文将介绍板弯曲荷载的计算公式及其应用。
板材的弯曲荷载计算公式一般可以通过弯曲理论和材料力学知识推导得出。
其中，常用的板材弯曲荷载计算公式包括弯曲应力公式、弯曲变形公式和板材的抗弯强度计算公式。
首先，我们来看看板材的弯曲应力计算公式。
板材在受到外力作用时，会产生弯曲应力。
弯曲应力是板材单位面积上的受力情况，可以通过以下公式计算：σ = M c / I。
其中，σ为板材的弯曲应力，M为板材上的弯矩，c为板材的截面中性轴到最外纤维的距离，I为板材的惯性矩。
通过这个公式，我们可以计算出板材在受到外力作用时的弯曲应力情况，从而确定板材的受力状态。
接下来，我们来看看板材的弯曲变形计算公式。
在受到外力作用时，板材会产生弯曲变形。
弯曲变形是板材在受力情况下发生的变形，可以通过以下公式计算：δ = M l / (E I)。
其中，δ为板材的弯曲变形，M为板材上的弯矩，l为板材的长度，E为板材的弹性模量，I为板材的惯性矩。
通过这个公式，我们可以计算出板材在受到外力作用时的弯曲变形情况，从而确定板材的变形情况。
最后，我们来看看板材的抗弯强度计算公式。
板材的抗弯强度是指板材在受到外力作用时所能承受的最大弯曲应力。
可以通过以下公式计算：f = M c / S。
其中，f为板材的抗弯强度，M为板材上的弯矩，c为板材的截面中性轴到最外纤维的距离，S为板材的截面模量。
通过这个公式，我们可以计算出板材在受到外力作用时的抗弯强度情况，从而确定板材的受力极限。
以上就是板材的弯曲荷载计算公式及其应用。
通过这些公式，我们可以计算出板材在受到外力作用时的受力情况、变形情况和抗弯强度情况，从而保证工程的安全性和稳定性。
在工程设计中，合理应用这些公式可以有效地指导工程实践，保证工程的质量和安全。
第六章弯曲变形判断弯曲变形1、“平面弯曲梁的挠曲线必定是一条与外力作用面重合或平行的平面曲线”2、“由于挠曲线的曲率与弯矩成正比，因此横截面的挠度与转角也与横截面的弯矩成正比”3、“只要满足线弹性条件，就可以应用挠曲线的近似微分方程”4、“两梁的抗弯刚度相同、弯矩方程相同，则两梁的挠曲线形状相同”5、“梁的挠曲线方程随弯矩方程的分段而分段，只要梁不具有中间铰，梁的挠曲线仍然是一条光滑、连续的曲线。
”6、“最大挠度处的截面转角一定为0”7、“最大弯矩处的挠度也一定是最大”8、“梁的最大挠度不一定是发生在梁的最大弯矩处。
”9、“只要材料服从虎克定律，则构件弯曲时其弯矩、转角、挠度都可以用叠加方法来求”10、“两根几何尺寸、支撑条件完全相同的静定梁，只要所受的载荷相同，则两梁所对应的截面的挠度和转角相同，而与梁的材料是否相同无关”11、“一铸铁简支梁在均布载荷的作用下，当其横截面相同且分别按图示两种情况放置时，梁同一截面的应力和变形均相同”选择弯曲变形1、圆截面的悬臂梁在自由端受集中力的作用，当梁的直径减少一半而其他条件不变时，最大正应力是原来的倍；最大挠度是原来的倍。
若梁的长度增大一倍，其他条件不变，最大弯曲正应力是原来的倍，最大挠度是原来的倍。
A：2； B：16 C：8 D：4；2、y’’=M(x)/EI在条件下成立。
A：小变形； B：材料服从虎克定律；C：挠曲线在xoy面内； D：同时满足A、B、C；3、等直梁在弯曲变形时，挠曲线最大曲率发生在处。
A：挠度最大； B：转角最大 C：剪力最大； D：弯矩最大；4、在简支梁中，对于减少弯曲变形效果最明显。
A：减小集中力P； B：减小梁的跨度；C：采用优质钢； D：提高截面的惯性矩5、板条弯成1/4圆，设梁始终处于线弹性范围内：①σ=My/I Z,②y’’=M(x)/EI Z哪一个会得到正确的计算结果？A：①正确、②正确；B：①正确、②错误； C:①错误、②正确； D：①错误、②错误；6、应用叠加原理求横截面的挠度、转角时，需要满足的条件是。
木材弯曲变形原因
一、木材弯曲变形原因
1.湿度的影响：在潮湿的环境下，木材容易吸收水分而发生弯曲；
2.力的影响：木材在受到外力作用时，会发生弯曲变形；
3.木材品种的影响：不同的木材品种，因其纤维的不同分布会对弯曲度产生影响；
4.木材结构的影响：木材的结构会对弯曲度产生影响，如截面形状和木材含水量的不同等。
二、解决方法
1.控制湿度：在木材加工过程中，要控制好木材的湿度，特别是在湿度较高的季节加工木材，要采取相应的措施，如在油漆表面刷一层防锈油等；
2.热压弯曲：经过热压后的木材，可以改变木材的结构，使得弯曲度得到控制；
3.使用强度高、材质均匀的木材；
4.使用钢筋等辅助材料，加强木材的支撑和承受力；
5.在木材旁边加装托板，防止木材因弯曲太大而破裂。
第8章 弯曲变形本章要点【概念】平面弯曲，剪力、弯矩符号规定，纯弯曲，中性轴，曲率，挠度，转角。
剪力、弯矩与荷载集度的关系；弯曲正应力的适用条件；提高梁的弯曲强度的措施；运用叠加法求弯曲变形的前提条件；截面上正应力分布规律、切应力分布规律。
【公式】 1. 弯曲正应力 变形几何关系：yερ=物理关系：Ey σρ=静力关系：0N AF dA σ==⎰，0y AM z dA σ==⎰，2zz AAEI EM y dA y dA σρρ===⎰⎰中性层曲率：1MEIρ=弯曲正应力应力：，My Iσ=，max max z M W σ=弯曲变形的正应力强度条件：[]maxmax zM W σσ=≤ 2. 弯曲切应力矩形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F bh F S S 2323max ==τ工字形梁弯曲切应力：dI S F y z z S ⋅⋅=*)(τ，A F dh F S S ==max τ圆形截面梁弯曲切应力：bI S F y z z S ⋅⋅=*)(τ，A F S 34max =τ弯曲切应力强度条件：[]ττ≤max3. 梁的弯曲变形梁的挠曲线近似微分方程：()''EIw M x =-梁的转角方程：1()dwM x dx C dx EIθ==-+⎰ 梁的挠度方程：12()Z M x w dx dx C x C EI ⎛⎫=-++ ⎪⎝⎭⎰⎰ 练习题一. 单选题1、 建立平面弯曲正应力公式zI My /=σ,需要考虑的关系有（）。
查看答案A 、平衡关系,物理关系，变形几何关系B 、变形几何关系，物理关系，静力关系；C 、变形几何关系，平衡关系，静力关系D 、平衡关系, 物理关系，静力关系；2、 利用积分法求梁的变形，不需要用到下面那类条件（）来确定积分常数。
查看答案A 、平衡条件B 、边界条件C 、连续性条件D 、光滑性条件3、 在图1悬臂梁的AC 段上，各个截面上的（）。
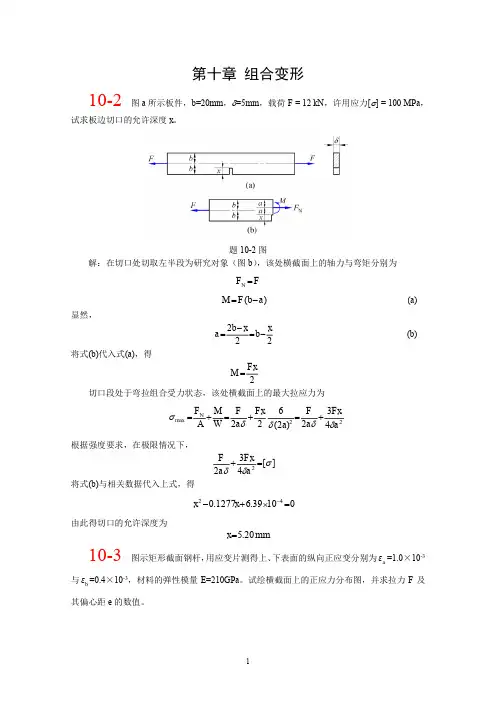
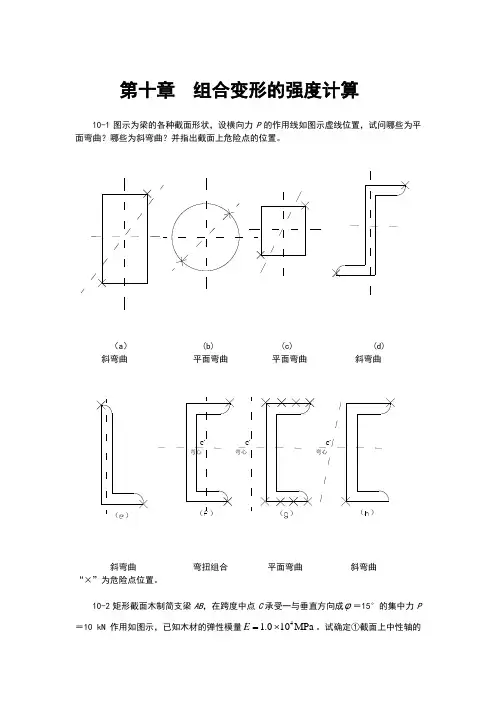
第十章 组合变形的强度计算10-1图示为梁的各种截面形状，设横向力P 的作用线如图示虚线位置，试问哪些为平面弯曲？哪些为斜弯曲？并指出截面上危险点的位置。
（a ） (b) (c) (d) 斜弯曲 平面弯曲 平面弯曲 斜弯曲弯心（）（）弯心弯心（）（）斜弯曲 弯扭组合 平面弯曲 斜弯曲“×”为危险点位置。
10-2矩形截面木制简支梁AB ，在跨度中点C 承受一与垂直方向成ϕ＝15°的集中力P ＝10 kN 作用如图示，已知木材的弹性模量MPa 100.14⨯=E 。
试确定①截面上中性轴的位置；②危险截面上的最大正应力；③C 点的总挠度的大小和方向。
解：66.915cos 10cos =⨯==οϕP P y KN59.215sin 10sin =⨯==οϕP P z KN4310122015=⨯=z J 4cm 3310cm W z =335625121520cm J y =⨯=3750cm W y =25.74366.94max =⨯==l P M y z KN-M 94.14359.24m ax =⨯==l P M z y KN-MMPaW M W M yy z z 84.9107501094.110101025.763633maxmax max=⨯⨯+⨯⨯=+=--σ 中性轴：οο47.2515tan 562510tan tan tan 411=⎪⎪⎭⎫ ⎝⎛-=⎪⎪⎭⎫⎝⎛-=--ϕαy z J J 2849333105434.0101010104831066.948--⨯=⨯⨯⨯⨯⨯⨯==z y y EJ l P f m28933310259.010562510104831059.248--⨯=⨯⨯⨯⨯⨯⨯==y z z EJ l P f m 602.0259.05434.022=+=f cm方向⊥中性轴：ο47.25=α10-3 矩形截面木材悬臂梁受力如图示，P 1＝800 N ，P 2＝1600 N 。
