理论力学 第八章 弯曲变形解析
- 格式:ppt
- 大小:3.22 MB
- 文档页数:63

如何在理论力学中分析弯曲和扭转效应?在工程和物理学领域,理解和分析弯曲和扭转效应是至关重要的。
弯曲和扭转是物体在受力作用下常见的变形形式,它们对于结构的稳定性、机械部件的性能以及材料的强度评估都有着深远的影响。
接下来,让我们逐步深入探讨如何在理论力学中对这两种效应进行有效的分析。
首先,我们来了解一下弯曲效应。
当一个杆件或梁受到垂直于其轴线的力时,就会产生弯曲。
为了分析弯曲,我们需要引入一些关键的概念和理论。
弯矩是描述弯曲效应的重要物理量。
它是力乘以力臂的乘积,反映了杆件在某一截面上所承受的弯曲力矩的大小。
通过计算不同截面上的弯矩,我们可以了解杆件在不同位置的弯曲程度。
在弯曲分析中,还需要考虑梁的截面特性。
例如,惯性矩就是一个关键的参数。
惯性矩取决于截面的形状和尺寸,它反映了截面抵抗弯曲变形的能力。
不同形状的截面,如圆形、矩形、工字形等,具有不同的惯性矩计算公式。
对于简单的静定梁,我们可以使用静力平衡方程来求解弯矩和剪力。
例如,简支梁在均布载荷作用下,通过对梁进行受力分析,列出平衡方程,就能够得到弯矩和剪力的表达式。
而对于超静定梁,就需要结合变形协调条件和物理方程来求解。
这可能会涉及到使用力法或位移法等较为复杂的分析方法。
接下来,我们转向扭转效应的分析。
当杆件受到绕其轴线的扭矩作用时,就会产生扭转。
扭矩是描述扭转效应的物理量,类似于弯矩在弯曲分析中的作用。
为了分析扭转,我们同样需要关注杆件的截面特性,其中极惯性矩是一个重要的参数。
对于圆形截面的杆件,其极惯性矩可以通过特定的公式计算得出。
而对于非圆形截面,计算极惯性矩则相对复杂。
在扭转分析中,还有一个重要的概念是剪应力分布。
在圆形截面的扭转中,剪应力沿着半径方向呈线性分布,最大剪应力出现在圆周表面。
对于复杂的扭转问题,如变截面杆件的扭转或多根杆件组成的系统的扭转,可能需要使用能量法或有限元方法等数值分析手段来求解。
在实际应用中,弯曲和扭转效应往往是同时存在的。

理论力学中的杆件的弯曲分析在理论力学中,杆件的弯曲分析是一项重要的研究内容。
杆件是指具有一定长度和截面形状的直线构件,广泛应用于工程领域中的结构设计和分析中。
杆件的弯曲行为是指杆件在受到外力作用下的偏转现象。
杆件的弯曲分析可以通过数学模型和物理实验相结合的方法来进行研究。
在理论力学中,最常用的方法是基于光滑杆的欧拉-伯努利梁理论。
该理论假设杆件在弯曲过程中,截面仍然保持平面,且杆件的变形主要由弯曲引起,而不考虑剪切变形和截面扭曲等其他因素。
这种理论适用于较细长、刚度较小的杆件的弯曲分析。
在杆件的弯曲分析中,主要涉及到弯矩、剪力和轴力等三个关键参数。
弯矩是指在杆件弯曲时,各点截面上受到的力矩。
剪力是指杆件上某一截面上垂直于杆件轴线的合力。
轴力是指作用在杆件上的沿轴线方向的拉力或压力。
在欧拉-伯努利梁理论下,可以通过建立弯曲方程和边界条件来求解杆件的弯曲行为。
对于简单支撑的杆件,在计算弯矩和偏转量时,可以利用弯曲方程进行求解。
弯曲方程可以通过平衡条件、力和位移之间的相互关系推导而来。
通过求解弯曲方程,可以得到不同位置上的弯矩和偏转量分布。
除了利用弯曲方程进行分析外,也可以通过物理实验来研究杆件的弯曲行为。
物理实验可以通过施加已知大小和作用点的外力来观察杆件的变形情况,并测量相应的弯矩和偏转量。
通过物理实验,可以验证理论模型的准确性,并对实际工程中的杆件设计提供参考依据。
在实际工程中,不同类型的杆件承受不同的弯曲载荷,因此对不同类型的杆件进行弯曲分析时需要考虑到其特殊条件和假设。
例如,对于非光滑杆件、较短小刚度杆件或受到较大剪力作用的杆件,需要采用其他的弯曲分析方法来求解。
此外,杆件的弯曲分析也可以与其他力学性能分析相结合,如杆件的稳定性分析和疲劳分析等。
综上所述,理论力学中的杆件的弯曲分析是对杆件在受到外力作用下变形行为的研究。
通过数学模型和物理实验相结合的方法,可以求解不同类型的杆件的弯曲行为,并为实际工程中的结构设计和分析提供依据。


理论力学中的杆件的变形分析杆件在力学中扮演着重要的角色,广泛应用于各种工程领域。
在理论力学中,对于杆件的变形进行分析是十分重要的,它能帮助工程师和设计师预测和评估结构的性能和可靠性。
本文将介绍杆件的变形分析的基本原理和方法。
1. 弹性变形杆件受到外力作用时,会发生弹性变形。
在弹性变形情况下,杆件会迅速恢复到未受力状态,且不会发生永久形变。
弹性变形是基于胡克定律,即应力与应变成正比。
根据胡克定律,可以得到杆件的弹性形变的方程。
2. 杆件的拉伸和压缩当杆件受到拉伸或压缩作用时,会发生轴向变形。
在理论力学中,我们可以使用材料力学的知识来分析杆件的轴向变形。
拉伸和压缩是杆件最常见的变形形式,例如,建筑物的柱子或者桥梁的支撑杆件都会经历拉伸或压缩。
3. 杆件的弯曲当杆件受到弯曲力矩作用时,会发生弯曲变形。
弯曲是指杆件在垂直于其长度方向上发生形状改变。
在理论力学中,我们可以使用梁的理论来分析杆件的弯曲变形。
通过应力和应变的关系以及几何形状的考虑,可以计算出杆件在弯曲过程中的变形情况。
4. 杆件的扭转当杆件受到扭矩作用时,会发生扭转变形。
扭转是指杆件在一个固定的截面上,某一段杆件相对于其他段发生旋转。
通过扭转变形分析,我们可以计算出杆件在扭转过程中的变形情况。
杆件的变形分析对于在工程设计过程中非常重要。
通过对杆件的变形情况进行准确的分析,可以帮助工程师和设计师了解结构的性能和可靠性。
此外,在设计过程中,合理地选择材料和截面形状也是非常关键的,因为不同的材料和截面形状会直接影响杆件的变形情况。
总之,理论力学中的杆件的变形分析是一个复杂但重要的领域。
它涉及到弹性变形、拉伸和压缩、弯曲和扭转等不同类型的变形。
通过对杆件变形进行准确的分析,可以帮助工程师预测结构的行为,并确保结构的性能和安全性。
对于工程设计和结构优化来说,杆件的变形分析是一项必不可少的工作。

第一章 绪论一、是非判断题1.1 材料力学的研究方法与理论力学的研究方法完全相同。
( ) 1.2 内力只作用在杆件截面的形心处。
( ) 1.3 杆件某截面上的内力是该截面上应力的代数和。
( ) 1.4 确定截面内力的截面法,适用于不论等截面或变截面、直杆或曲杆、基本变形或组合变形、横截面或任意截面的普遍情况。
( ) 1.5 根据各向同性假设,可认为材料的弹性常数在各方向都相同。
( ) 1.6 根据均匀性假设,可认为构件的弹性常数在各点处都相同。
( ) 1.7 同一截面上正应力ζ与切应力η必相互垂直。
( ) 1.8 同一截面上各点的正应力ζ必定大小相等,方向相同。
( ) 1.9 同一截面上各点的切应力η必相互平行。
( ) 1.10 应变分为正应变ε和切应变γ。
( ) 1.11 应变为无量纲量。
( ) 1.12 若物体各部分均无变形,则物体内各点的应变均为零。
( ) 1.13 若物体内各点的应变均为零,则物体无位移。
( ) 1.14 平衡状态弹性体的任意部分的内力都与外力保持平衡。
( )1.15 题1.15图所示结构中,AD 杆发生的变形为弯曲与压缩的组合变形。
( )1.16 题1.16图所示结构中,AB 杆将发生弯曲与压缩的组合变形。
( )二、填空题1.1 材料力学主要研究 受力后发生的 ,以及由此产生的 。
1.2 拉伸或压缩的受力特征是 ,变形特征是 。
1.3 剪切的受力特征是 ,变形特征是 。
1.4 扭转的受力特征是 ,变形特征是 。
B题1.15图题1.16图1.5 弯曲的受力特征是 ,变形特征是 。
1.6 组合受力与变形是指 。
1.7 构件的承载能力包括 , 和 三个方面。
1.8 所谓 ,是指材料或构件抵抗破坏的能力。
所谓 ,是指构件抵抗变形的能力。
所谓 ,是指材料或构件保持其原有平衡形式的能力。
1.9 根据固体材料的性能作如下三个基本假设 , , 。

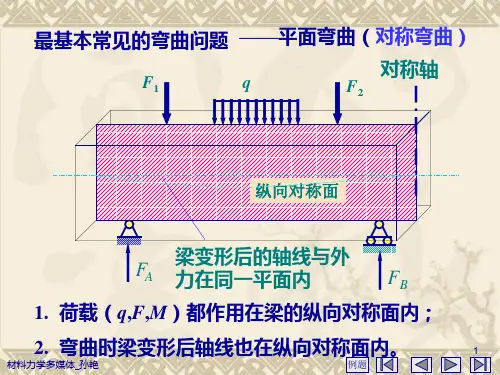
理论力学中的梁的弯曲和剪切问题如何处理?在理论力学的研究领域中,梁的弯曲和剪切问题是一个重要且常见的课题。
无论是在建筑结构、机械设计还是航空航天等工程领域,理解和处理梁的弯曲和剪切问题都至关重要。
梁,作为一种常见的结构元件,在承受外部载荷时会发生弯曲和剪切变形。
要处理这些问题,首先我们需要明确梁的基本概念和分类。
从形状和受力特点来看,梁可以分为简支梁、悬臂梁和连续梁等。
简支梁两端支撑,悬臂梁一端固定一端自由,连续梁则是由多个梁段通过中间支座连接而成。
不同类型的梁在受力和变形特性上有所差异。
当梁受到垂直于其轴线的载荷时,就会产生弯曲。
在这种情况下,梁的上部分受到压缩,下部分受到拉伸,而在梁的中间存在一个既不压缩也不拉伸的中性层。
为了描述梁的弯曲程度,我们引入了曲率的概念。
梁的弯曲问题可以通过建立弯矩方程来解决。
弯矩是指梁截面上由于弯曲而产生的内力偶矩。
通过对梁进行受力分析,可以确定每个截面处的弯矩大小。
然后,根据材料力学的知识,利用弯矩与弯曲应力和弯曲变形之间的关系来计算梁的应力和变形。
在处理梁的弯曲应力时,常用的公式是弯曲正应力公式和弯曲切应力公式。
弯曲正应力与弯矩成正比,与截面的惯性矩成反比。
而弯曲切应力则与剪力和截面的形状有关。
对于常见的矩形截面梁,弯曲切应力在中性轴处达到最大值。
接下来谈谈梁的剪切问题。
剪切力是指在梁的横截面上平行于截面的内力。
当梁受到横向载荷时,除了产生弯曲变形外,还会产生剪切变形。
在处理梁的剪切问题时,我们需要考虑剪切应变和剪切应力。
剪切应变是指梁在剪切力作用下发生的角度变形,而剪切应力则是单位面积上的剪切力。
对于梁的剪切强度计算,通常需要考虑材料的剪切强度极限和梁的截面形状等因素。
在一些情况下,剪切变形可能对梁的性能产生较大影响,特别是在短粗梁或者受到较大横向载荷的梁中。
为了更准确地分析梁的弯曲和剪切问题,我们还可以借助一些数值方法,如有限元分析。
有限元分析可以将梁离散为多个小单元,通过计算每个单元的应力和变形,进而得到整个梁的力学响应。




理论力学中的弯曲力与弯矩的计算与分析在理论力学中,弯曲力和弯矩是研究杆件和结构受力性质的重要参数。
弯曲力和弯矩的计算与分析对于设计和分析结构的性能和安全性具有重要意义。
本文将介绍弯曲力和弯矩的计算和分析方法,并提供相关的理论和实例。
一、理论力学中的弯曲力和弯矩弯曲是指杆件或结构在受力作用下发生的变形现象,其中弯曲力和弯矩是描述弯曲行为的重要参量。
弯曲力是垂直于杆件剖面的力,它导致杆件产生弯曲变形。
弯曲力的计算可以通过受力分析和力矩平衡得到,常用的计算公式为:M = F * d,其中M为弯矩,F为弯曲力,d为力臂,即力对应的点到杆件轴线的距离。
弯矩是杆件内部产生的抵抗弯曲变形的力矩。
在理论力学中,根据弯曲力和杆件的几何形状,可以通过弯矩公式计算弯矩的大小。
对于梁的弯曲,弯矩的计算公式为:M = EI * κ,其中M为弯矩,E为杨氏模量,I为截面惯性矩,κ为曲率。
二、弯曲力与弯矩的计算与分析1. 弯曲力的计算与分析弯曲力的计算与分析主要涉及受力分析和力矩平衡。
在实际工程中,可以通过使用杆件的受力平衡方程来计算弯曲力的大小。
受力平衡方程是指对于杆件受力状态下,所有作用力的代数和等于零。
通过解方程组可以求解出各个力的大小。
另外,根据杆件的几何形状和弯曲情况,可以利用仿真软件进行弯曲力的计算与分析。
常用的仿真软件有有限元分析软件,如ANSYS、ABAQUS等。
通过建立合适的模型和载荷条件,可以模拟杆件在不同受力情况下的弯曲行为,并计算出相应的弯曲力。
2. 弯矩的计算与分析弯矩的计算与分析主要涉及杆件的几何形状和弯曲情况。
对于简单形状的杆件,可以通过几何关系和受力平衡方程来计算弯矩的大小。
而对于复杂形状的杆件,可以利用截面性质和弯曲理论来进行计算与分析。
截面性质是指杆件剖面的几何参数,如截面面积、惯性矩等。
根据截面性质和弯曲理论,可以利用弯矩公式计算出弯矩的大小。
而弯曲理论根据杆件的几何形状和受力情况,提供了不同的弯矩计算方法,如Euler-Bernoulli弯曲理论和Timoshenko弯曲理论等。
理论力学中的圆环梁的弯曲分析引言理论力学是研究物体受力学作用下运动和变形规律的学科,圆环梁则是一种常见的结构。
本文旨在对理论力学中的圆环梁的弯曲分析进行探讨,重点介绍圆环梁的基本原理、计算方法以及应用。
一、圆环梁的基本原理圆环梁是一种环形断面的梁材,在受到弯曲力作用下会发生变形。
为了研究圆环梁的弯曲分析,我们首先需要了解圆环梁的基本原理。
1.1 圆环梁受力特点在应用中,圆环梁常常承受径向负载和弯曲力矩。
与直线梁相比,圆环梁由于其特殊的断面形状,具有一些独特的受力特点,比如材料密度不均匀、分布不规则的孔洞等。
这些特点会影响到圆环梁的弯曲分析。
1.2 圆环梁的变形规律在受到弯曲力作用下,圆环梁会发生弯曲变形。
通过应变-位移关系和材料的本构关系,我们可以得到圆环梁的变形规律。
这对于圆环梁的弯曲分析具有重要意义。
二、圆环梁的计算方法在实际工程中,我们需要用到合适的计算方法来分析圆环梁的弯曲性能。
下面介绍两种常用的计算方法。
2.1 基于解析解的计算方法基于解析解的计算方法是指通过求解适当的微分方程,得到圆环梁的弯曲解析解。
这种方法在一些简单情况下可以得到较为准确的结果,但对于复杂情况则相对困难。
2.2 基于数值计算的计算方法基于数值计算的计算方法是指利用计算机进行离散化计算,对圆环梁的受力和变形进行数值模拟。
这种方法相对灵活,可以适用于各种复杂情况,但需要注意选取合适的数值计算模型和参数。
三、圆环梁的应用领域由于圆环梁具有独特的结构特点和力学行为,它在许多领域都有重要的应用。
3.1 圆环梁在建筑结构中的应用在建筑结构中,圆环梁常常应用于拱桥、建筑穹顶等。
通过对圆环梁的弯曲分析,可以确保结构的强度和稳定性。
3.2 圆环梁在机械设计中的应用在机械设计中,圆环梁常常用于轴承支撑、发动机悬挂等部件。
通过对圆环梁的弯曲分析,可以优化设计,提高机械系统的性能和可靠性。
结论本文对理论力学中的圆环梁的弯曲分析进行了探讨,介绍了圆环梁的基本原理、计算方法以及应用。
理论力学中的弯曲理论如何应用?在工程和科学领域中,理论力学的弯曲理论是一个至关重要的概念。
它不仅有助于我们理解物体在受到外力作用时的弯曲行为,还为实际应用中的设计和分析提供了坚实的理论基础。
弯曲理论主要研究的是细长杆件或结构在受到横向载荷作用时的变形和内力分布。
当我们考虑一个简单的梁,比如在建筑结构中的钢梁或者机械装置中的传动轴,弯曲理论就能够帮助我们预测它们在承受负载时的弯曲程度以及内部产生的应力。
在建筑结构设计中,弯曲理论的应用极为广泛。
例如,在设计桥梁时,工程师需要考虑车辆和行人的重量对桥梁梁体产生的弯曲效应。
通过弯曲理论的计算,可以确定桥梁梁体所需要的尺寸、材料强度以及支撑结构的布置,以确保桥梁在使用过程中能够安全地承受各种载荷而不发生过度的弯曲变形甚至破坏。
机械工程领域同样离不开弯曲理论。
像汽车的传动轴,在传递动力的过程中会受到扭转和弯曲的复合作用。
利用弯曲理论,工程师能够精确计算出轴在不同工作条件下的弯曲应力和变形,从而选择合适的材料和轴的直径,保证传动轴的可靠性和使用寿命。
在航空航天领域,飞机的机翼结构设计也是弯曲理论的重要应用场景之一。
机翼在飞行过程中承受着空气动力产生的升力和阻力,这些力会导致机翼发生弯曲变形。
通过弯曲理论的分析,可以优化机翼的结构,减轻重量的同时保证其强度和刚度满足飞行要求。
在材料科学中,弯曲理论对于研究材料的力学性能也具有重要意义。
通过对材料制成的试件进行弯曲实验,并结合弯曲理论的公式,可以得到材料的弹性模量、屈服强度等关键力学参数。
这些参数对于评估材料的质量和选择合适的材料用于特定的应用至关重要。
对于一些复杂的结构,如框架结构或者空间桁架结构,弯曲理论同样可以发挥作用。
虽然这些结构的受力情况较为复杂,但通过将其分解为单个杆件的弯曲问题,并综合考虑节点的连接方式和约束条件,仍然可以利用弯曲理论进行有效的分析和设计。
在实际应用中,弯曲理论的计算通常基于一些基本假设。