当前位置：文档之家 › hj1-3 直梁的弯曲解析

hj1-3 直梁的弯曲解析

  • 格式：ppt
  • 大小：2.05 MB
  • 文档页数：84

下载文档原格式

  / 84

合集下载

直梁的弯曲

直梁的弯曲
MC,MA的坐标相连，画出 抛物线；再以直线MA,MD左 和MD右，MB的坐标，可得 全梁的弯矩图图c所示。 由图可见，在D稍右处横
截面上有绝对值最大的弯 矩，其值为
M 15kN m max
例题分析
例题4-1：管道托架如图所示，如AB长为l，作用在其上的 管道重P1与P2，单位为kN，a、b、l以m计。托架可简化 为悬臂梁，试画出它的弯矩图。
例题分析
例题4-2：卧式容器可以简化为受均布载荷的外伸梁，如图 所示受均布载荷q作用的筒体总长L，试作出其弯矩图，并 讨论支座放在什么位置使设备的受力情况最好。
解：(1)共分三个受力段， 如图建立坐标系yAx．
(2)求支座反力RC、RD RC＝RD ＝0.5qL
例题分析
(3)列弯矩方程，画弯矩图
例题分析
解：共分为三个受力段，取 梁左端A为坐标原点，建立 坐标系，如图：
•分段列弯矩方程，画弯矩图：
M1=0 (0≤x1 ≤ a)
M
M2=－P1 (x2 －a)
(a ≤ x2 ≤ b)
M3=－P1 (x3 －a) －P2 (x3 －b)
(b ≤ x3 ≤ l)
x
x
-
－P1 (b －a) －P1 (l －a) －P2 (l －b)
bh2
IZ 12
WZ 6
IZ
D 4
64
(1
4)
WZ
D3
32
(1
4)
截面几何量Iz 与Wz
其它截面形状的Iz 和Wz（参见表４－２）
对各种型钢，Iz 和Wz值可从有关材料手册中查到
❖结论：１）梁在弯矩相同的截面上， Iz 和Wz值 越大， σmax越小，因此设计梁的截面形状时，要 尽量使Iz 和Wz值大； ２）梁在弯矩相同的截面上， Iz和Iy可能不同，Wz 和Wy可能不同，因此若将梁沿轴向转90º，其承载 能力不同。

工程力学教学资料-第八章 直梁的弯曲

工程力学教学资料-第八章 直梁的弯曲

直梁的弯曲
1、平面弯曲的概念 2、梁的计算简图 3、剪力和弯矩 4、剪力图和弯矩图 5、用叠加法作弯矩图 6、剪力、弯矩和荷载 集度间的关系 7、工程中的弯曲变形 问题 8、用积分法求梁的弯 曲变形 9、用叠加法求弯曲变 形 10、梁的刚度计算 11、静不定梁
12、用莫尔定理计算 梁的弯曲变形直梁的弯曲Fra bibliotek直梁的弯曲
1、平面弯曲的概念 2、梁的计算简图 3、剪力和弯矩 4、剪力图和弯矩图 5、用叠加法作弯矩图 6、剪力、弯矩和荷载 集度间的关系 7、工程中的弯曲变形 问题 8、用积分法求梁的弯 曲变形 9、用叠加法求弯曲变 形 10、梁的刚度计算 11、静不定梁
1.虚功原理
12、用莫尔定理计算 梁的弯曲变形
12、用莫尔定理计算 梁的弯曲变形
直梁的弯曲
1、平面弯曲的概念 2、梁的计算简图 3、剪力和弯矩 4、剪力图和弯矩图 5、用叠加法作弯矩图 6、剪力、弯矩和荷载 集度间的关系 7、工程中的弯曲变形 问题 8、用积分法求梁的弯 曲变形 9、用叠加法求弯曲变 形 10、梁的刚度计算 11、静不定梁
（2）选择合理的截面形状
（3）选用弹性模量较大的材料
12、用莫尔定理计算 梁的弯曲变形
直梁的弯曲
1、平面弯曲的概念 2、梁的计算简图 3、剪力和弯矩 4、剪力图和弯矩图 5、用叠加法作弯矩图 6、剪力、弯矩和荷载 集度间的关系 7、工程中的弯曲变形 问题 8、用积分法求梁的弯 曲变形 9、用叠加法求弯曲变 形 10、梁的刚度计算 11、静不定梁
12、用莫尔定理计算 梁的弯曲变形
直梁的弯曲
1、平面弯曲的概念 2、梁的计算简图 3、剪力和弯矩 4、剪力图和弯矩图 5、用叠加法作弯矩图 6、剪力、弯矩和荷载 集度间的关系 7、工程中的弯曲变形 问题 8、用积分法求梁的弯 曲变形 9、用叠加法求弯曲变 形 10、梁的刚度计算 11、静不定梁

机械设备基础 三 直梁的弯曲

机械设备基础 三 直梁的弯曲

梁的变形
P l3 ql4 fB 3E JZ 8E JZ
例：等截面悬臂梁的自由端作用一集中力，梁的抗弯刚 度为EJz，求此梁的挠曲线方程以及自由端截面的转角 和挠度。 EJ f M ( x ) P ( L x ) Z
1 2 PLx EJ Px C Zf 2 1 2 1 3 EJ f PLx Px Cx D Z 2 6
2 hb 1 W A b z2 6 6
因h>b，则Wz1>Wz2；这说明矩形截面的梁直立时比横放时 具有较高的抗弯强度。
材料远离中性轴
塑性材料
脆性材料
等 截 面 梁
等 强 度 梁
第七节 梁的弯曲变形
外力 内力 应力 强度条件 刚度条件
工程 应用
一、梁的挠度和转角
变形后梁的轴线称为弹性曲线或挠曲线 挠度 f，梁的挠曲线方程 f = f(x) 转角θ
max
M WZ
四、横力弯曲
以上有关纯弯曲的正应力的公式，对于横力弯曲的情 形，如果是细长杆，也是近似适用。理论与实验结果都表
明，由于剪应力的存在，梁的横截面在变形之后将不再保
持平面，而是要发生翘曲，此时平面假设和各纵向纤维不
互相挤压不成立。而对于细长梁，这种翘曲对正应力的影
响是很小的。通常都可以忽略不计。 均布载荷作用下的矩形截面简支梁，L/h>5时，按纯
2 h / 2 2 h / 2 2
3
第五节
梁弯曲时的强度条件
Mm ax m ax W Z
利用强度条件，可对梁进行强度校核、选择截面尺寸及确定许可荷载。
例3-7: 容器四个耳座支架在四根各长2.4m的工字钢梁的中点上，工字钢再由四根混凝 土柱支持。容器包括物料重110kN，工字钢为16号型钢，钢材弯曲许用应力 [σ]=120MPa，试校核工字钢的强度。

直梁的弯曲 PPT

直梁的弯曲 PPT
直梁的弯曲
1
拉（压）杆：承受轴向拉、压力 轴 ：承受扭矩
墙
桥板 楼板 梁：承受横向力
工程实际中的弯曲问题
P
P
P
P
梁的弯曲实例与概念
受力特点：力垂直于构件的轴线(力偶在轴线平面)； 变形特点：杆的轴线将由直线变成曲线 以弯曲变形为主的杆件在工程上统称为梁。
4
桥式吊车
5
火车轮轴
6
车削工件
7
纵向对称面：通过梁的轴线和截面对称轴的平面。 矩形截面梁有一个纵向对称面
4. 梁支座反力
利用静力学平衡方程求支座反力：
X 0, Y 0, M 0
y
R Ax A
P
l/2
Bx
RBy
X 0 Y 0
M
A
R Ay
RAx 0
l
RAy RBy P 0
RBy l P l / 2 0
0
RBy P / 2 RAy P / 2
RB
2. 从弯曲变形看弯矩
加载后发生弯曲：
1 ）纵向纤维变成了 弧线，凹入边纵向纤 维 m1m2 缩短了，突出 边 n1 n2 伸 长 了 ， O1O2长度不变。 2 ） 横 向 线 a1 b1 、 a2b2仍为直线，说明 变形前的横截面变 形后仍然保持为平
A
a
C
P
P
D
a
B
面。
3）a1b1与a2b2不再平行（互相倾斜），说明横截 面a1b1与a2b2发生了相对转动。
y
0 RA P Q2 0
Q2 RA P
注意这里Q2为负
m
O
(F ) 0 M 2 RA x2 P( x2 a) 0

第七章 直梁的弯曲

第七章 直梁的弯曲

A1B1 AB A1B1 O1O2 AB O1O2
( y )dq dq y dq

y

...... (1)
（二）物理关系： 根据胡克定律，应力在材料的比例极限内，应力与应变的规律：
E
Ey

...... (2)
（三）静力学关系： 中性轴Z是通过截面形心且与纵向对称轴垂直，中性层的 曲率为：
d
D
ad
D
I D3 W= (1 a 4 ) 0.1 D3 (1 a 4 ) ymax 32
1 A 1m 1
Q=60kN/m B 2m 180 30 1 2
例1 受均布载荷作用的简支梁
如图所示，试求： （1）1——1截面上1、2两点 的正应力； （2）此截面上的最大正应力；
（3）全梁的最大正应力；
求应力
bh3 1201803 Iz 1012 5.832105 m 4 12 12
120 y + qL2 8 Mmax
z
Wz I z / 2 6.48104 m3
1 2
M1 y Iz
x
60 60 105 61.7MP a 5.832
M
XA A P1 B P2 C YA YB
梁的计算简图
在计算简图中，通常以梁的轴线表示梁。作用在梁 上的载荷，一般可以简化为三种形式:
1.集中力:
2.集中力偶: 3.分布载荷(均 布载荷)
第二节 梁弯曲时横截面的内力 1. 基本概念
y
aa
A
A
F F
b
b
B
B
1 x
1
1
c
c

三章直梁的弯曲

三章直梁的弯曲

镗刀杆
直梁的弯曲
P
直梁的弯曲
火车轮轴
直梁的弯曲
把以弯曲为主要变形的杆称为
直梁的弯曲
梁 (Beam)
工程中的梁横截面一般都是对称的。
P
P
P
纵向对称面
直梁的弯曲
平面弯曲(Plane bending)
•具有纵向对称面
•外力都作用在此面内（受力特点）
挠曲线
•弯曲变形后轴线变成对称面内的平面曲线（变形特点）
xm A nl
Q M
直梁的弯曲
P
力平衡：Q - P = 0
B
力矩平衡：M + P(l-x) = 0
P 弯矩：M = - P(l-x)
B
（问题：按左半边梁，能算出M吗？）
A QM
直梁的弯曲
例 一简支梁受力如图所示。试求C截面（跨中截面） 上的弯矩。
M1 2qa2 q
M2 2qa2
A
B
C
RA
a
4a
a
则为负。
+M
+M
-M -M
同一位置处左、右侧截面上内力分量必须具有相 同的正负号。
直Hale Waihona Puke 的弯曲弯矩—截面一侧所有外力对截面形心力矩的代数和
弯:M 矩 1RAx1
M 2 R A x 2 P x 2 a
弯矩等于该横截面一侧所有外力对该截面形心取力矩的代数和。 梁上向上的外力均产生正弯矩；而向下的外力均产生负弯矩。 截面左侧顺时针转向的力偶或截面右侧逆时针转向的力偶取正 值，反之取负值。
梁的类型
简支梁
( Simply Supported Beam )
外伸梁
(Overhanging Beam)

第四章 直梁的弯曲 化工机械设备基础

第四章 直 梁 的 弯 曲
1
一. 弯曲的概念与梁的分类 二. 梁的内力分析 三. 纯弯曲时梁的正应力及正应力 强度条件
四. 梁的变形——梁弯曲时的位移
2
第一节 弯曲的概念与梁的分类
一、弯曲变形的宏观表现和实例
桥板
3
起重机大梁
P
4
目录
火车轮轴
5
火车轮轴简化
6
弯曲特点：
P P
受力特点：受到垂直于杆件轴线的外力（即横 向力）或力偶的作用 变形特点：杆件的轴线由原来的直线变成曲线 以弯曲变形为主的杆件通常称为梁。
7-2
y y( x )
dy tan dx
63
二.梁的刚度校核
1.刚度条件
y max [ y ],
max [ ]
l l ~ 建筑钢梁的许可挠度： 250 1000 1 机械传动轴的许可转角： 3000
精密机床的许可转角：
7-5
1 5000
64
本章小结:
一 、梁的种类和支座种类 二、剪力和弯矩的计算 三、弯曲正应力的强度条件
据此法则： 截面左侧 Q左=RA －P1 截面右侧 Q右=P2 + P3 －RB
25
2 弯矩的计算
弯矩的符号约定
M M
+
M
-
M
上压下拉为正
上拉下压为负
26
27
计算弯矩法则：梁在外力作用下，其任意指定截面
上的弯矩等于该截面一侧所有外力对该截面中性轴取 矩的代数和；凡是向上的外力，其矩取正；向下的外 力，其矩取负值。
21
二、剪力与弯矩的计算
剪力：抵抗该截面一侧所有外力对该截面的剪
切作用，大小应该等于该截面一侧所有横向外力 之和。

直梁的弯曲及组合变形与压杆稳定——教案

直梁的弯曲及组合变形与压杆稳定——教案第一章：直梁的弯曲1.1 弯曲的概念解释直梁弯曲的定义展示直梁弯曲的图像1.2 弯曲的原因讨论引起直梁弯曲的各种因素，如载荷、材料属性等1.3 弯曲的受力分析分析直梁弯曲时的受力情况介绍剪力、弯矩等概念1.4 弯曲变形的基本公式推导直梁弯曲变形的微分方程介绍剪切应力、弯曲应力等概念第二章：组合变形2.1 组合变形的概念解释组合变形的定义展示组合变形的图像2.2 组合变形的原因讨论引起组合变形的原因，如载荷组合、材料属性等2.3 组合变形的受力分析分析组合变形时的受力情况介绍组合剪力、组合弯矩等概念2.4 组合变形的基本公式推导组合变形的基本公式介绍组合剪切应力、组合弯曲应力等概念第三章：压杆稳定3.1 压杆稳定的概念解释压杆稳定的定义展示压杆稳定的图像3.2 压杆失稳的原因讨论引起压杆失稳的原因，如长细比、载荷等3.3 压杆稳定的受力分析分析压杆稳定时的受力情况介绍压杆的轴向应力、剪切应力等概念3.4 压杆稳定的判断方法介绍压杆稳定的判断方法，如临界力计算、稳定系数等第四章：直梁弯曲的计算4.1 剪力与弯矩的计算介绍剪力与弯矩的计算方法给出剪力与弯矩的计算实例4.2 弯曲应力的计算介绍弯曲应力的计算方法给出弯曲应力的计算实例4.3 弯曲变形的计算介绍弯曲变形的计算方法给出弯曲变形的计算实例第五章：组合变形的计算5.1 组合剪力与组合弯矩的计算介绍组合剪力与组合弯矩的计算方法给出组合剪力与组合弯矩的计算实例5.2 组合应力的计算介绍组合应力的计算方法给出组合应力的计算实例5.3 组合变形的计算介绍组合变形的计算方法给出组合变形的计算实例5.4 组合变形的控制讨论组合变形的控制方法，如限制长细比、增加支撑等第六章：压杆稳定的计算与控制6.1 临界力的计算介绍压杆失稳时的临界力计算方法给出临界力的计算实例6.2 稳定系数的计算介绍稳定系数的计算方法给出稳定系数的计算实例6.3 压杆稳定的控制讨论压杆稳定的控制方法，如限制长细比、增加支撑等第七章：直梁弯曲与压杆稳定的应用实例7.1 直梁弯曲的应用实例分析实际工程中的直梁弯曲问题给出直梁弯曲问题的解决方案7.2 压杆稳定的应用实例分析实际工程中的压杆稳定问题给出压杆稳定问题的解决方案第八章：组合变形的应用实例8.1 组合变形的应用实例分析实际工程中的组合变形问题给出组合变形问题的解决方案8.2 组合变形与直梁弯曲、压杆稳定的综合应用实例分析实际工程中的组合变形、直梁弯曲和压杆稳定问题给出综合问题的解决方案第九章：直梁弯曲、组合变形与压杆稳定的实验研究9.1 直梁弯曲的实验研究介绍直梁弯曲实验的方法和步骤分析实验结果与理论计算的对比9.2 组合变形的实验研究介绍组合变形实验的方法和步骤分析实验结果与理论计算的对比9.3 压杆稳定的实验研究介绍压杆稳定实验的方法和步骤分析实验结果与理论计算的对比第十章：直梁弯曲、组合变形与压杆稳定的现代计算方法10.1 有限元法在直梁弯曲、组合变形与压杆稳定分析中的应用介绍有限元法的基本原理分析有限元法在直梁弯曲、组合变形与压杆稳定分析中的应用实例10.2 优化方法在直梁弯曲、组合变形与压杆稳定优化设计中的应用介绍优化方法的基本原理分析优化方法在直梁弯曲、组合变形与压杆稳定优化设计中的应用实例10.3 方法在直梁弯曲、组合变形与压杆稳定分析中的应用介绍方法的基本原理分析方法在直梁弯曲、组合变形与压杆稳定分析中的应用实例重点和难点解析重点环节1：直梁弯曲的受力分析与弯曲应力的计算受力分析中剪力与弯矩的分布是理解直梁弯曲的关键。

【精编】直梁的弯曲-教案2021

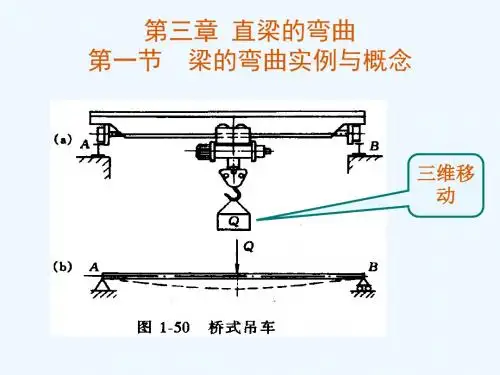
学习必备欢迎下载内蒙古科技大学教案化工设备机械基础课程名称：3 直梁的弯曲授课章节目的要求掌握梁的剪力弯矩方程和剪力弯矩图重点难点剪力弯矩方程举例引入新课一、梁的概念及其分类（约 5 分钟）介绍桥式吊车、卧式容器、受风载荷的塔设备、管道托架的弯曲1、梁的概念及其特点把以弯曲为主要变形的杆称为梁。

介绍及其类梁的概念特点和分工程中的梁横截面一般都是对称的。

（矩形、圆环形、工字形、丁字形）受力特点：力偶或垂直于轴线的外力作用在一个通过轴线平面内。

变形特点：杆件的轴线（力偶或横向力）由直线变为曲线。

2、梁的分类简支梁：（10 分钟）外伸梁（卧式容器）悬臂梁（承受风载荷的塔）二、梁的内力分析对受用的到外力作梁进行内梁在外力作用下、内部将产生力分析内力。

为求出梁横截面1-1 上的内力、采用截面法、外力有支座约束反力Q 1。

截面上还应有一个力偶M 、以满足平衡方程∑M=0 、该力偶与外力对截面1-1形心O 的力矩相平衡。

第7 次第 1 页1、 截面法求内力—剪力 Q 和弯矩 M剪 力 与 弯 矩 概 述剪力 —截面一侧所有竖向分力的代数和 ;弯矩 —截面一侧所有外力对截面形心力矩的代数和。

内力 Q 称为横截面上的剪力。

内力偶 M 称为横截面上的弯矩。

因此、 梁弯曲时的内力包括剪力 Q 与弯矩 M 。

运用静力平衡方程求图中 1-1 和 2-2 截面上 的剪力和弯矩。

（截面法、 合力为零、正；弯矩方向：左顺右逆为正）（10 分钟）2、梁内力的简便求法 —— “外力简化法 ” 梁 的 剪 力 计 算方法a 1 P 1Q R P 1 A 1M 1M 1 R A x P 1(x a 1)oxQ 1R Aa 2 x Q 1 P 2 R B（10 分钟）M 1 R B (l x) P 2(a 2 x)o lQ 1xR B例题：简支梁、 求 1-1、例题分析（1）求支反力 R A 、R BM 0,AF y （2）求内力练习题：试求 1-1、2-2 截面的弯曲内力。

《直梁的弯曲》课件

《直梁的弯曲》PPT课件
本课程将帮助您理解直梁的弯曲，包括定义、应用案例，以及实际应用中的 受力分析等方面。
直梁的定义
1 形态多样
2 材料广泛
直梁可以是长方形、圆形、 梯形、等腰三角形，还可 以是不规则截面，具有很 强的适应性。
直梁可以是钢、木材、混 凝土等多种材料，根据实 际情况选用不同材料可以 使得设计更加符合实际。
3 用途广泛
直梁用于桥梁工程、建筑 工程、机械制造等领域， 是一项非常重要的工程基 础。
采用欧拉-伯努利梁理论
基本假设
梁的截面上任意点的平面仍保 持平面状态，不发生大变形。
导出方程
欧拉-伯努利梁理论是从平衡方 程、应变-位移关系和恒定体积 原理出发导出的。
适用范围
该理论假设梁的变形很小，仅 适用于杆件长度较大、截面尺 寸较小的杆件。
2
跨河大桥建设
建设跨河大桥需要使用钢梁，而钢梁又需要经过精准的计算和设计，方能达到给定的跨度和 承重能力。
3
机械制造中的应用
在机械制造行业，还会使用直梁的弯曲原理来进行设计和计算，准确的计算对机械的使用寿 命和安全性大有裨益。
结论与展望
弯曲问题解决
通过本课程，您已经了解了直梁的弯曲和相关 应用，能够对各种弯曲问题做出准确的分析。
梁受力分析
弯矩分析
计算梁的弯曲应变，通过弯矩分 析得到相关参数。
轴力分析
梁受到压力和张力作用，分析力 的产生和传递。
剪力分析
梁受到剪力的作用，分析梁受剪 切变形带来的影响。
应用案例分析
1
地铁路基工程
地铁是当今城市中交通工具使用最频繁的，而交通干道、大楼和其他设施往往会影响到地铁， 需要使用直梁解决问题。
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018/10/17
14
二、内力图—剪力图和弯矩图
作图时用梁的轴线为横坐标，
表示各截面的位置；用纵坐标 表示相应截面上的弯矩值，并 且规定正弯矩画在横坐标的上 面，负弯矩画在横坐标的下面， 这样画出来的图形就叫弯矩图。
2018/10/17 15

例3-1．管道托架如图a。如AB长为l，单位为 m，作用在其上的管道重P1与P2，单位为kN， a、b以m计。托架可简化为悬臂梁，试画出它 的弯矩图。
2018/10/17

弯矩等于该横截面一侧所有外力对该 截面形心取力矩的代数和。梁上向上 的外力均产生正弯矩；而向下的外力 均产生负弯矩。
截面左侧顺时针转向的力偶或截面右 侧逆时针转向的力偶取正值，反之取 负值
13

2018/10/17
第三节 弯矩方程与弯矩图
一、剪力方程式和弯矩方程式
Q Q( x ) M M ( x)
2018/10/17
5
梁的基本形式
简支梁：一端固定铰链，另一端活动铰链； 外伸梁：简支梁一端或两端伸出支座以外； 悬臂梁：一端固定，另一端自由。
外力—内力—应力—强度条件和刚度条件
2018/10/17
6
第二节 梁横截面上的内力 — 剪力和弯矩
一、截面法求内力—剪力Q和弯矩M
2018/10/17
7
剪力：Q1 RA
弯矩（内力偶矩）： M1 RA x1
2018/10/17 8
Q2=P-RA
M 2 RA x2 Px2 a
2018/10/17 9
内力符号规定如下：
通常根据梁的变形来规定其正负号： 当梁向下凹弯曲，即下侧受拉，弯矩 规定为正值；当梁向上凸弯曲，即上 侧受拉，弯矩规定为负值。
2018/10/17 10
剪力：Q Fy
剪力：Q1 RA
Q2 RA P
左侧梁上向上的外力或右侧梁上向下的 外力引起的剪力为正，反之为负，剪力 等于该侧外力的代数和。
2018/10/17 11
弯矩 : M mO F
弯矩 : M1 RA x1

12
M 2 RA x2 Px2 a
21
1 R A RB ql 2
2018/10/17 22
ql Q( x) RA qx qx 2 x ql qx2 M ( x) RA x qx x 2 2 2
M
max
1 2 ql 8
2018/10/17
23

如果是集中力 P=ql用在梁的中 点，画出来的弯 矩图如下图，最 大弯矩在集中力 P所在的横截面 上，等于，比均 布载荷时大一倍。
Pb RA l
29
Pb Q( x1 ) R A l Pb M ( x1 ) R A x1 x1 l
a Q( x2 ) RA P P l
(0 x1 a) (0 x1 a)
(a x2 l ) (a x2 l )
30
Pb M ( x2 ) RA x2 P( x2 a) x2 P( x2 a) l
第三章 直梁的弯曲
第一节 梁的弯曲实例与概念
2018/10/17
1
以弯曲为主要变形的构件在工程上称 为梁
2018/10/17
2
2018/10/17
3
20向对称平面内，受 到垂直于梁的轴线的力或力偶作用，使构 件的轴线在此平面内弯曲为曲线，这样的 弯曲称为平面弯曲.
2018/10/17
Pa RB l
Pb RA l
(0 x1 a) (0 x1 a)
Pb Q( x1 ) R A l Pb M ( x1 ) R A x1 x1 l
a Q( x 2 ) R A P P l
(a x 2 l ) (a x 2 l )
mC M ( x2 ) RA x2 mC x2 mC l
mC Q( x2 ) RA l
(a x2 l ) (a x2 l )
例3-5．简支梁在C点处受集中荷载P 作用，画出此梁的剪力图和弯矩图。
2018/10/17
28
Pa RB l
2018/10/17
2018/10/17
19

1.写弯矩方程式。以B点为原点，这样可避免 求支座反力，x轴向右为正，从右边自由端考 虑列任意截面n-n处的弯矩方程式：

2.画弯矩图 （考虑如果在B点作用集中力）
20
2018/10/17
例3-3．简支梁受集度为q的均布荷 载作用，画出此梁的剪力图和弯矩 图。
2018/10/17
Pb M ( x 2 ) R A x 2 P( x 2 a) x2 P( x 2 A) l

例3-6．卧式容器可以简化为受均布载荷的 外伸梁。图a表示受均布载荷q作用的筒体 总长L。问支座放在什么位置使设备的受力 情况最好。
2018/10/17
32

1．求支座反力。首先求支座反力RA与RB，显 然
2018/10/17
33

2．写弯矩方程式。
外伸段1-1截面的弯矩方程为： 这一段中，当x=a时，弯矩最大值为 中间段2-2截面的弯矩方程为：
2018/10/17
34
因此，鞍座位置应满足a=0.2L
2018/10/17 35




结论： (1)梁受集中力作用时，弯矩图必为直线， 并且在集中力作用处，弯矩发生转折。 (2)梁受力偶作用时，弯矩图也是直线，但 是，在力偶作用处，弯矩发生突变，突变 的大小等于力偶矩。 (3)梁受均布载荷作用时，弯矩图必为抛物 线，如均布载荷向下，则抛物线开口向下， 如均布载荷向上，则抛物线开口向上。
2018/10/17
16


1．建立弯矩方程。 根据截面左边梁上的外力，按前述直接从外力 计算的方法，写出弯矩方程如下：
2018/10/17
17

2．作弯矩图。
2018/10/17
18

例3-2．塔器可以 简化为具有固定 端支座的悬臂梁， 如图。风压为均 布载荷q，单位为 kN／m，l的单位 用m表示，画它 的弯矩图。
2018/10/17
24
例3-4．简支梁在C处受一集中力偶mC的作 用，画出剪力图和弯矩图。
2018/10/17
25
mC R A RB l
2018/10/17 26
mC Q( x1 ) RA l mC M ( x1 ) RA x1 x1 l
(0 x1 a) (0 x1 a)