三角形的高

各种三角形的高
作者：邹卫东
来源：《小学生学习指导_趣味课堂·中年级》2019年第04期
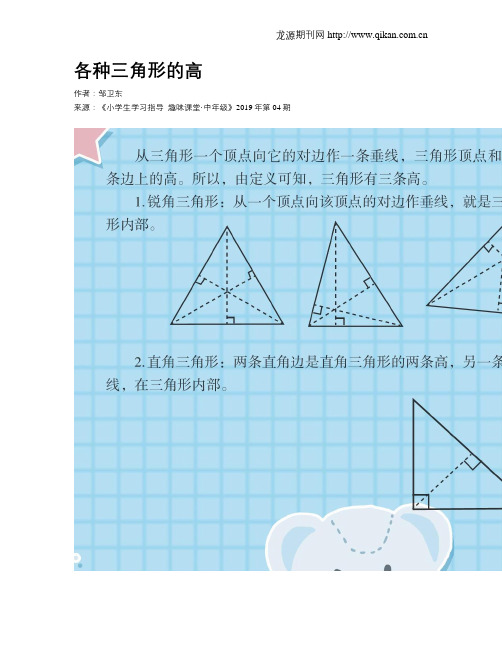
从三角形一个顶点向它的对边作一条垂线，三角形顶点和垂线之间的线段称三角形这条边上的高。

所以，由定义可知，三角形有三条高。

1.锐角三角形：从一个顶点向该顶点的对边作垂线，就是三角形的高，三条高都在三角形内部。

2.直角三角形：两条直角边是直角三角形的两条高，另一条高是直角顶点向斜边作的垂线，在三角形内部。

3.钝角三角形：钝角顶点向对边作垂线是一条高，在三角形内部，钝角的两边上的高在它们的延长线上，在三角形的外部。

《虚虚岛》参考答案
1.4
2.一個考了54分，一个考了0分
3.五十一
4.坐立不安
5.不同凡响
6.0。

三角形面积求高的公式
三角形的高的求法：高=三角形面积×2÷底。

根据公式：三角形面积=（底×高）/2可知：底×高=2面积；底=三角形面积×2÷高。

三角形是由同一平面内不在同一直线上的三条线段“首尾”顺次连接所组成的封闭图形，在数学、建筑学有应用。

三角形的性质：
1、三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点。

2、三角形三条中线的长度的平方和等于它的三边的长度平方和的3/4。

3、等底同高的三角形面积相等。

4、底相等的三角形的面积之比等于其高之比，高相等的三角形的面积之比等于其底之比。

5、三角形的任意一条中线将这个三角形分为两个面积相等的三角形。

计算三角形的高度三角形是几何学中的基础形状，计算三角形的高度是解决许多与三角形相关问题的关键步骤。

本文将介绍如何计算三角形的高度，以及应用高度的一些实际例子。

1. 什么是三角形的高度？在三角形中，高度是从三角形的一个顶点到对边（这条边上不包含这个顶点）所作的垂直连线的长度。

每个三角形都有三条高度，它们交于同一个点，称为三角形的垂心。

2. 如何计算三角形的高度？计算三角形的高度可以利用三角形的面积和底边的长度。

根据公式，三角形的面积等于底边长度乘以高度再除以2。

因此，可以通过重新排列这个公式来计算高度：高度等于2倍的面积除以底边的长度。

具体步骤如下：a) 首先，根据提供的信息确定底边的长度。

b) 然后，根据已知的底边长度和三角形的面积，使用这个公式计算高度。

c) 最后，得到三角形的高度值。

3. 应用高度的实际例子a) 建筑设计：在建筑设计中，计算三角形的高度对于确定建筑物的尺寸和比例非常重要。

例如，在设计一个屋顶的高度时，需要计算房顶三角形的高度。

b) 地理测量：在地理测量中，计算三角形的高度可以用于确定山峰或其他地形的高度。

通过测量两个观测点之间的水平距离和仰角，可以计算出目标地点的高度。

c) 飞行导航：在飞行导航中，计算三角形的高度可以用于确定飞机的高度或飞行路径上的障碍物的高度。

通过测量两个观察点之间的水平距离和仰角，可以计算出目标物体的高度。

d) 水资源管理：在水资源管理中，计算三角形的高度对于确定水库或水塘的蓄水量非常重要。

通过测量水面的面积和底边的长度，可以计算出水的体积。

总结：计算三角形的高度是解决与三角形相关问题的重要步骤。

通过使用三角形的面积和底边的长度，可以计算出三角形的高度。

在建筑设计、地理测量、飞行导航和水资源管理等领域，应用高度的知识非常重要。

了解如何计算三角形的高度可以帮助我们更好地理解和解决各种实际问题。

三角形三个高与对应边的比例关系
三角形的三个高分别与对应边的比例关系如下：
1. 三角形的高与底边之间的比例关系：三角形的高与底边之间的比例是固定的。

无论三角形的形状如何，只要两个三角形有相似关系，它们的高与底边之间的比例就相同。

2. 三角形的高与斜边之间的比例关系：对于直角三角形，高等于斜边乘以正弦角的值；对于非直角三角形，高与斜边之间的比例关系没有固定的公式，而是通过计算三角形的三边长度和角度来确定。

3. 三角形的高与边长之间的比例关系：三角形的高与边长之间没有固定的比例关系，而是依赖于三角形的形状和角度。

总之，三角形的三个高分别与对应边的比例关系取决于三角形的形状、角度和边长。

三角形求高的公式面积=S=1/2×底×高其中，底代表三角形的任意一条边，高代表从底到顶点的垂直距离。

对于一般的三角形，要求得三角形的高需要额外的条件。

下面将讨论两种特殊情况。

1.对于直角三角形：直角三角形是指其中一个角为直角的三角形。

直角三角形的性质是，直角的边被称为斜边，其余两边被称为直角边。

对于一个直角三角形，可以利用勾股定理来求解三角形的高。

勾股定理表述如下：c²=a²+b²其中，c代表斜边的长，a和b分别代表直角边的长。

以直角三角形的直角边a为底，以斜边c作为高，根据面积公式求得：S=1/2×a×c代入勾股定理的表达式：S=1/2×a×√(c²-a²)因此，直角三角形的高公式为：高=√(c²-a²)2.对于等边三角形：等边三角形是指三条边的长度都相等的三角形。

等边三角形的性质是，每个内角都是60度。

对于一个等边三角形，可以利用正弦定理来求解三角形的高。

正弦定理表述如下：a/sinA = b/sinB = c/sinC = 2R其中，a、b、c分别代表三边的长度，A、B、C分别代表对应的内角，R代表三角形外接圆的半径。

对等边三角形来说，每个内角都是60度，由于三角形的三边长度都相等，可以将正弦定理表示为：a/sin60° = b/sin60° = c/sin60° = 2R由sin60°=√3/2，上述表达式可以化简为：a/√3=b/√3=c/√3=2R由此可以得到等边三角形的高公式：高=h=a×√3/2其中，a代表等边三角形的边长，h代表等边三角形的高。

以上就是两种特殊情况下求解三角形高的公式。

对于一般的三角形，我们还可以利用三角形的内切圆来求解三角形高。

三角形的内切圆是指与三角形的三边都接触的一个圆，该圆的半径被称为内切圆的半径。

三角形的高三角形的高，这可是数学世界里一个相当有趣的概念！咱们先来说说什么是三角形的高。

想象一下，你有一个三角形的蛋糕，想要把它切成平均的小块，那从顶点直直切到底边的那条线，就是三角形的高啦。

还记得我之前教过的一个小学生，叫小明。

那时候，我们正在学习三角形的高，小明怎么都搞不明白。

我就给他举了个例子，说：“小明啊，你看咱们教室的房梁，从屋顶到地面，是不是就像三角形的高？”他眨眨眼睛，还是一脸迷茫。

于是我拿出一张纸，画了一个大大的三角形，然后跟他说：“小明，你把这个三角形想象成一座山，山顶有一个小亭子，你要从亭子走到山脚下，走的最短的那条路就是高。

”这次，小明好像有点明白了，但是在做练习题的时候，又犯糊涂了。

三角形的高啊，其实有很多种情况。

比如锐角三角形，它的三条高都在三角形内部；直角三角形呢，两条高就是它的两条直角边；钝角三角形就有点特别啦，它的两条高在三角形外面。

我再给你讲讲我在课堂上的一次小经历。

有一次，我让同学们自己动手画三角形的高，有个同学画得歪歪扭扭的，我就走过去问他：“你这是画的高吗？怎么像小蛇在跳舞呀？”同学们都哈哈大笑起来，那个同学也不好意思地挠挠头。

那怎么来画三角形的高呢？其实很简单。

比如一个锐角三角形，先找到一个顶点，然后对着对边，用直角三角板的一条直角边和三角形的一条边重合，另一条直角边过这个顶点，沿着这条直角边画的线就是高啦。

在生活中，三角形的高也有很多用处呢。

比如说建房子的时候，工人师傅要计算房梁的高度，就得用到三角形的高的知识；还有设计师设计桥梁的时候，也得考虑三角形结构中高的问题，这样才能保证桥梁坚固又美观。

回到学习上，同学们在做关于三角形高的题目时，一定要仔细看清题目要求，是让你画高，还是计算高的长度。

可别像小明一开始那样，迷迷糊糊的。

我希望大家都能像探索宝藏一样，去发现三角形的高的奥秘，把这个知识牢牢地掌握在自己手里。

说不定以后你自己设计个小玩意儿，或者解决一个大难题，都能用到它呢！总之，三角形的高虽然只是数学中的一个小知识点，但它的作用可不小。

三角形的高定理在几何学中，三角形是最基本的几何形状之一，而三角形的高定理是描述三角形内部的高与底边之间的关系的一个重要定理。

本文将介绍三角形的高定理，并探讨其应用和证明。

一、三角形的高定理的表述三角形的高定理指出，在一个三角形中，三条高的长度之和等于这个三角形中最长边的长度。

二、三角形的高定理的应用三角形的高定理在解决几何问题时具有重要的应用价值。

通过这个定理，我们可以求解三角形的高，并进一步获得有关三角形各边长和角度的信息。

以一个具体的例子来说明：假设我们有一个三角形，其中两边长分别为5cm和7cm，夹角为60度。

现在我们想要求解这个三角形的高。

根据三角形的高定理，我们知道，在三角形中，高的长度之和等于最长边的长度。

所以我们可以通过求解最长边来进一步计算出其他两条高的长度。

首先，我们需要确定这个三角形的最长边。

通过观察可知，边长为7cm的一边是最长边。

由于这条边与夹角60度的边相邻，我们可以利用三角函数来求解。

根据三角函数的定义，我们可以得知，三角形中的一个角的正弦等于这个角的对边长度与斜边长度之比。

而在这个例子中，我们已知夹角是60度，边长为7cm的一边为斜边，而我们要求解的是与这个边相邻的边的长度。

通过正弦函数的计算，我们可以得到正弦60度等于根号3除以2。

进一步计算得到与边长为7cm的边相邻的边的长度约为7乘以根号3除以2，约等于6.06cm。

现在，我们已经求解出了三角形的最长边与相邻边的长度，接下来可以使用三角形的高定理求解三角形的高。

根据定理，三条高的长度之和等于最长边的长度。

因此，高的长度之和约为6.06cm 加上5cm，再加上7cm，等于约18.06cm。

三、三角形的高定理的证明三角形的高定理的证明可以通过几何推理和运用三角函数进行。

首先，我们可以通过几何推理证明出三角形的高与底边垂直。

这是因为高与底边之间的连线可以看作是底边所在直线上的垂线，根据几何学的基本概念，垂线与底边相交的角度为90度，即垂直。