三角形的高的画法与表示

数学导案授课教师齐晓宁迟源授课班级七年级授课时间2013年3月5日课题三角形的高、中线与角平分线导学目标1、理解并掌握三角形的三条线段的定义、画法以及表示方法；2、理解三角形的三条线段所表示的意义；3、体会转化数学思想。

导学重难点三角形的三条线段的画法以及表示方法导学流程个案补充一、知识互动1、三角形的高线（1）定义：从三角形的一个顶点向它的对边所在的直线作，和之间的线段。

（2）图形：（3）表示方法：①AD是△ABC的BC边上的高线②AD⊥BC于D③∠ADB=∠ADC=90°（4）请画出△ABC另两条边上的高以及△MAN、△DEF的三条高，从高线的位置角度考虑，得出什么结论?2、三角形的中线（1）定义：三角形中，连接一个顶点和它对边的线段。

（2）图形：（3）表示方法：①AE是△ABC的BC边上的中线②BC EC BE 21== （4）请画出△ABC 另两条边上的中线以及△MAN 、△DEF 的三条中线，从中线的位置考虑，你得出什么结论?（5）三角形的三条中线相交于一点，这个交点叫做三角形的重心。

3、三角形的角平分线（1）定义：三角形的一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段。

（2）图形：（3）表示方法：①AM 是△ABC 的∠BAC 的平分线； ②BAC ∠=∠=∠2121 （4）请画出△ABC 另两条角平分线以及△MAN 、△DEF 的三条角平分线，从角平分线的位置考虑，你得出什么结论?（5）三角形的三条角平分线相交于一点，这个交点叫做三角形的内心。

【注】三角形的高、中线、角平分线都是 ；二垂线是 ； 角平分线是 。

二、例题讲解例1 如图1所示，图中共有 6 个三角形，若BC=CD=DE ，则AC 、AD 分别是 △ABD 、 △ACE 的中线。

图1 图2例2 如图2所示，已知AD、AE分别是△ABC的高和中线，AB=6cm,AC=8cm ,BC=10cm，∠CAB=90°。

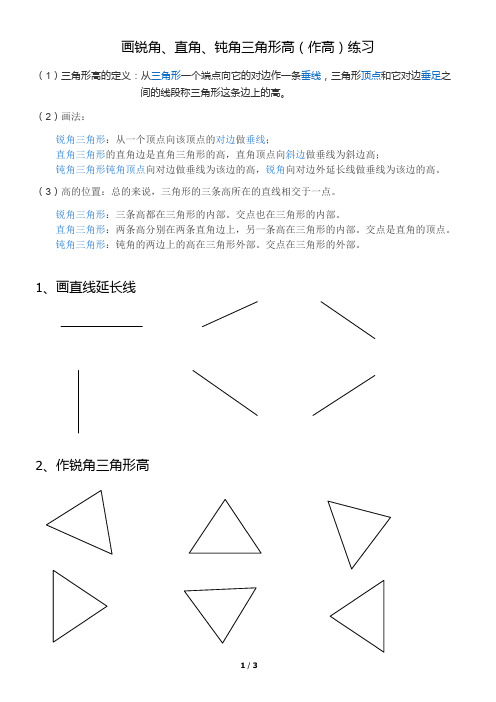
画锐角、直角、钝角三角形高（作高）练习
（1）三角形高的定义：从三角形一个端点向它的对边作一条垂线，三角形顶点和它对边垂足之
间的线段称三角形这条边上的高。

（2）画法：
锐角三角形：从一个顶点向该顶点的对边做垂线；
直角三角形的直角边是直角三角形的高，直角顶点向斜边做垂线为斜边高；
钝角三角形钝角顶点向对边做垂线为该边的高，锐角向对边外延长线做垂线为该边的高。

（3）高的位置：总的来说，三角形的三条高所在的直线相交于一点。

锐角三角形：三条高都在三角形的内部。

交点也在三角形的内部。

直角三角形：两条高分别在两条直角边上，另一条高在三角形的内部。

交点是直角的顶点。

钝角三角形：钝角的两边上的高在三角形外部。

交点在三角形的外部。

1、画直线延长线
2、作锐角三角形高。

小学三角形知识点总结_小学三角形面积公式大全_小学三角形的定义
·小学数学：三角形知识点
1、三角形的特性
①、三角形的定义：由三条线段围成的图形每相邻两条线段的端点相连或重合，叫做三角形。

②、从三角形的一个顶点到它的对边做一条垂线，顶点和垂足间的线段叫做三角形的高，这条对边叫做三角形的底。

三角形只有3条高。

重点：三角形高的画法。

画高：三角板的一条直角边与底对齐重合，另外一条直角边通过底相对应的顶点，沿着直角边画一条虚线，标上直角符号和高。

简记：一重，二过，三画，四标。

分别画出它的三条高：
锐角三角形的三条高都在三角形内;直角三角形有两条高落在两条直角边上直角三角形的两条直角边互为“底”和“高”;钝角三角形有两条高在三角形外
规定：为了表达方便，用字母A、B、C分别表示三角形的三个顶点，三角形可表示成三角形ABC。

切记：三角形有三条边，三个内角，三个顶点。

易错题：直角三角形只有一条高。

×
③、三角形的特性：三角形具有稳定性也就是当一个三角形的三条边的长度确定后，这个三角形的形状和大小都不会改
变，生活中很多物体利用了这样的特性。

如：人字梁、斜拉桥、自行车车架。

④、三角形边的特性：三角形任意两边的和大于第三边。

方法：已知三角形的两边分别是a和b,则第三边的范围是：
a-b第三边
技巧:判断三条线段是否能围成三角形，只要把最短的两
条边相加与最长变比较即可。

如果最短的两条边之和大于第三边，也就证明任意两条边之和大于第三边。

梯形、平行四边形和三角形的高的画法
问题导入你能画出下面图形中给定底边上的高吗？试一试，画一画。

（教材51页例题）
方法讲解
1．梯形高的画法
把三角尺的一条直角边与梯形的一条底边重合，另一条直角边与另一条底边相交于一点，从这一点向对应底边（或底边延长线）作垂线，这点到对应底边（或底边延长线）的垂直线段就是梯形的高，如下图所示：
2．平行四边形高的画法
把三角尺的一条直角边与平行四边形的一条底边重合，另一条直角边与平行四边形这条底边所对的边相交于一点，从这一点向底边（或底边延长线）作垂线，这点到底边（或底边沿长线）的垂直线段就是平行四边形的高，如下图所示：
3．三角形高的画法
(1)把三角尺的一条直角边与一条底边重合，沿着这个底边平移三角尺，使另一条直角
边通过底边所对的顶点。

(2)从顶点向底边画一条垂线，顶点到底边（或底边延长线）的垂直线段就是三角形底
边上的高。

如果是直角三角形，两条直角边就分别是三角形的底和高；如果是钝角三角形，画从两个锐角顶点所引的高时，可将底边延长（延长部分用虚线），再画高，如下图所示：
归纳总结
1．梯形的高的画法：从梯形的上底（或下底）任意找一点，向下底（或上底）画垂线，两底之间的垂直线段就是梯形的高。

2．平行四边形的高的画法：以任意一边为底，从对边的一点向底边画垂线，两底之间的垂直线段就是平行四边形的高。

3．三角形的高的画法：可以选三角形任意一边为底，从底边所对的顶点作底边的垂线，顶点和底边之间的垂直线段就是三角形的高。