解实系数一元二次方程

如何分解一元二次方程分解一元二次方程是解决一元二次方程的重要方法之一，也是应用数学中经常使用的技巧。

通过分解一元二次方程，我们可以将复杂的方程化简为两个一次方程，并进一步求解得到方程的根。

本文将详细介绍一元二次方程的分解方法，帮助读者有效地解决类似的数学问题。

首先，我们需要了解一元二次方程的一般形式：ax^2 + bx + c = 0。

其中，a、b、c分别是方程的系数，x代表未知数，0表示等式的右边为零。

解一元二次方程的关键是找到方程的两个因式，使得它们的乘积等于c，而求和等于b。

接下来，我们将详细介绍两种常见的一元二次方程分解方法：因式分解与配方法。

一、因式分解方法：1. 如果c是一个正数，我们需要找到两个正数的乘积等于c。

例如，对于方程x^2 + 5x + 6 = 0，我们需要找到两个正数，使得它们的乘积等于6，同时它们的和等于5。

显然，这两个数是2和3，因此我们可以将方程分解为(x + 2)(x + 3) = 0。

根据乘法的零乘性质，我们可以令(x + 2) = 0或(x + 3) = 0，并解得x的值分别为-2和-3。

2. 如果c是一个负数，我们需要找到一个负数和一个正数的乘积等于c，并且它们的和等于b。

例如，对于方程x^2 - 4x - 5 = 0，我们需要找到一个负数和一个正数，使得它们的乘积等于-5，同时它们的和等于-4。

通过试探法，我们可以得到这两个数是-5和1，因此我们可以将方程分解为(x- 5)(x + 1) = 0。

同样地，根据乘法的零乘性质，我们可以令(x - 5) = 0或(x + 1) = 0，并解得x的值分别为5和-1。

二、配方法：配方法是一种通过变形的方式将一元二次方程转化为一个可以因式分解的形式。

这种方法适用于当我们很难直接找到两个数使得其乘积等于c，而a的值不等于1的情况。

1. 首先，我们将一元二次方程的首项与末项进行乘法运算。

例如，对于方程2x^2 - 7x - 3 = 0，我们可以得到2*(-3) = -6。

解一元二次方程课标解读一、课标要求包括配方法、公式法、因式分解法解一元二次方程．?义务教育数学课程标准〔 2022年版〕?对解一元二次方程一节相关内容提出的要求如下。

1．理解配方法，能用配方法、公式法、因式分解法解数字系数的一元二次方程．2．会用一元二次方程根的判别式判别方程是否有实根和两个实根是否相等．3．了解一元二次方程的根与系数的关系．二、课标解读1．学生已经学习一元一次方程的解法和实际应用，知道可以利用运算律、等式的根本性质，通过去括号、移项、合并同类项等求出它的解．学生还学过二元一次方程组以及三元一次方程组的解法和实际应用，知道可以通过消元，将它们转化为一元一次方程．从数学知识的内部开展看，二元、三元一次方程组可以看成是对一元一次方程在“元〞上的推广．自然地，如果在次数上做推广，首先就是一元二次方程．类比二〔三〕元一次方程组的解法，可以想到：能否将一元二次方程转化为一元一次方程？如何转化？因此，利用什么方法将“二次〞降为“一次〞，这是本章学习的另一条主线．与一元一次方程、二元一次方程组的解法相比，一元二次方程的解法涉及更多的知识，可以根据方程的具体特点，选择相关的知识和方法，对方程进行求解．这是培养学生的思维品质，特别是思维的敏捷性、灵活性、深刻性的时机．根据?课程标准〔 2022年版〕?的规定，教科书着重介绍了配方法、公式法和因式分解法等一元二次方程的解法，而且限定解数字系数的一元二次方程．2．解一元二次方程的根本策略是降次，即通过配方、因式分解等，将一个一元二次方程转化为两个一元一次方程来解．具体地，根据平方根的意义，可得出方程和的解法；通过配方，可将一元二次方程转化为的形式再解；一元二次方程的求根公式，就是对方程配方后得出的．如能将分解为两个一次因式的乘积，那么可令每个因式为0来解．一元二次方程的三种解法——配方法、公式法和因式分解法各有特点．一般地，配方法是推导一元二次方程求根公式的工具．掌握了公式法，就可以直接用公式求一元二次方程的根了．当然，也要根据方程的具体特点，选择适当的解法，因式分解法就显示了这样的灵活性．配方法是一种重要的、应用广泛的数学方法，如后面研究二次函数时也要用到它．在推导求根公式的过程中，从到再到，是方程形式的不断推广，表达了从特殊到一般的过程；而求解方程的过程那么是将推广所得的方程转化为已经会解的方程，表达了化归思想．显然，这个过程对于培养学生的推理能力、运算能力等都是很有作用的．3．与?课程标准〔实验稿〕?相比，?课程标准〔 2022年版〕?重新强调了一元二次方程根的判别式和一元二次方程根与系数关系的重要性，要求“会用一元二次方程根的判别式判别方程是否有实根和两个实根是否相等〞，“了解一元二次方程的根与系数的关系〞，这是需要注意的一个变化．这里不仅是为了一元二次方程理论的完整性，更重要的是为了解决初高中衔接问题．实际上，一元二次方程根的判别式、一元二次方程根与系数关系在高中数学中有着广泛的应用，是学习高中数学的必备根底．教科书先以一个设计人体雕像的实际问题作为开篇，并在第一节中又给出两个实际问题，通过建立方程，并引导学生思考这些方程的共同特点，从而归纳得出一元二次方程的概念、一般形式，给出一元二次方程根的概念．在这个过程中，通过归纳具体方程的共同特点，定义一元二次方程的概念，表达了研究代数学问题的一般方法；一般形式也是对具体方程从“元〞〔未知数的个数〕、“次数〞和“项数〞等角度进行归纳的结果；a ≠0的规定是由“二次〞所要求的，这实际上也是从不同侧面理解一元二次方程概念的契机．一元二次方程的解法，包括配方法、公式法和因式分解法等，是全章的重点内容之一．教科书在第二节中，首先通过实际问题，建立了一个最简单的一元二次方程，并利用平方根的意义，通过直接开平方法得到方程的解；然后将它一般化为，通过分类讨论得到其解的情况，从而完成解一元二次方程的奠基．接着，教科书安排“探究〞栏目，自然引出解并总结出“降次〞的策略，从而为用配方法解比拟复杂的一元二次方程做好铺垫，然后教科书重点讲解了配方的步骤，并归纳出通过配方将一元二次方程转化为后的解的情况．以配方法为根底，教科书安排了“探究〞栏目，引导学生自主地用配方法解一般形式的一元二次方程(a≠0)，得到求根公式．最后，通过实际问题，获得一个显然可以用“提取公因式法〞而到达“降次〞目的的方程，从而引出因式分解法解一元二次方程，并在“归纳〞栏目中总结出几种解法的根本思路、各自特点和适用范围等．上述过程的思路自然，表达了从简单的、特殊的问题出发，通过逐步推广而获得复杂的、一般的问题，并通过将一般性问题化归为特殊问题，获得这一类问题的解．这是具有普适性的数学思想方法．由于限定在实数范围，因此对求根公式，首先要关注判别式的讨论．这是使学生领悟分类讨论数学思想方法的契机．另一方面，求根公式不仅直接反映了方程的根由系数唯一确定〔系数a，b，c确定，方程就确定，其根自然就唯一确定〕，而且也反映了根与系数的联系．这里表达了一种多角度看问题的思想观点，而根与系数的联系表达非常简洁．教科书仍然采用从特殊到一般的方法，先讨论“将方程化为的形式，，与p，q之间的关系〞，在“+，〞的启发下，利用求根公式求和，进而得到根与系数的关系．让学生学习根与系数的关系，不仅能深化对一元二次方程的理解，提高用一元二次方程分析和解决问题的能力，而且也是培养学生发现和提出问题的能力的时机．根与系数的关系是求根公式的自然延伸，得出它的过程并不复杂，而其中蕴含的思想很重要．所以，对于根与系数的关系，教科书着重在其数学思想的启发和引导上，而对用根与系数的关系去解决问题，严格地控制了难度．。

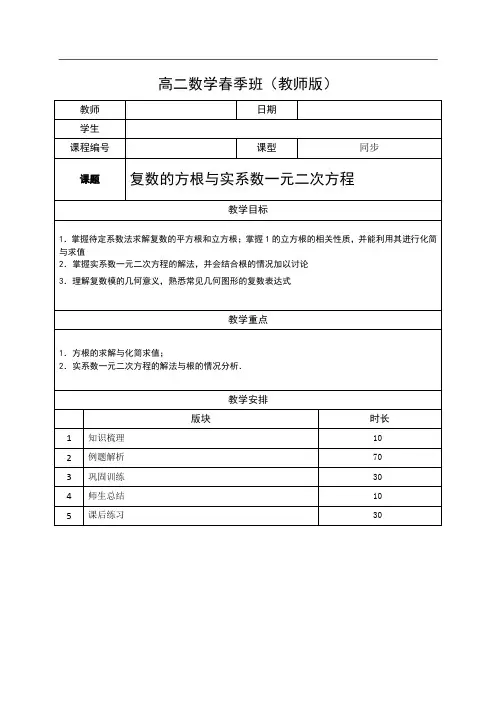
高二数学春季班（教师版）一、复数的平方根与立方根 1．复数的平方根的定义若复数1z ，2z 满足212z z =，则称1z 是2z 的平方根．2．复数的平方根的求法2()(,,,)a bi c di a b c c +=+∈R即利用复数相等，把复数平方根问题转化为实数方程组来求． 3．复数的平方根的性质复数(0)z z ≠总有两个平方根1z ，2z ，且120z z +=（见图1）． 4．复数的立方根的定义类似的，若复数1z ，2z 满足312z z =，则称1z 是2z 的立方根．5．1的立方根设复数12ω=-+，则21,,ωω都是1的立方根． 6．ω的性质 ①210ωω++=， ②31ω=，③212ωω==-． 可运用这些性质化简相关问题（见图2）． 7．其他有用结论2(1)2i i -=-，2(1)2i i +=二、实系数一元二次方程实系数一元二次方程20(,,,0)ax bx c a b c a ++=∈≠R 中的24b ac ∆=-为根的判别式，那么（1）0∆>⇔方程有两个不相等的实根2b a-±；复数的方根与实系数一元二次方程知识梳理（2）0∆=⇔方程有两个相等的实根2b a-； （3）0∆<⇔，在（3）的情况下，方程的根与系数关系（韦达定理）仍然成立． 求解复数集上的方程的方法：（1）设(,)z x yi x y =+∈R 化归为实数方程来解决（化归思想）．（2）把z 看成一个未知数（而不是实部和虚部两个未知数），用复数的性质来变形（整体思想）． （3）对二次方程，直接用一元二次方程的求根公式（公式法）．三、常见几何图形的复数表达式复数1z ，2z 为定值，且12z z ≠．（1）线段12Z Z 的中垂线方程：12||||z z z z -=-； （2）以1Z 为圆心，半径为r 的圆方程：1||z z r -=； （3）以1Z 、2Z 为焦点，长轴长为2(0)a a >的椭圆方程：12||||2z z z z a -+-=（其中12||2z z a -<）； （4）以1Z 、2Z 为焦点，实轴长为2(0)a a >的双曲线方程：12||||||2z z z z a ---=（其中12||2z z a ->）．1、复数的平方根与立方根 【例1】求4-及86i -的平方根．【难度】★【答案】4-的平方根为2i 或2i -；86i -的平方根为3i -或3i -+ 【例2】计算：（112112(1)22i i i ⎛⎫-+ ⎪⎝⎭；（2）50820028)i +-++⎝⎭． 【难度】★★【答案】（1）513；（2）247+【例3】记12ω=-，求1ωω+，221ωω+． 【难度】★★ 【答案】11ωω+=-，2211ωω+=-【例4】已知等比数列123,,,,n z z z z ，其中11z =，2z x yi =+，3z y xi =+（,,0x y x ∈>R ）．（1）求,x y 的值； （2）试求使1230n z z z z ++++=的最小正整数n ；（3）对（2）中的正整数n ，求123n z z z z 的值．【难度】★★【答案】（1）12x y ⎧=⎪⎪⎨⎪=⎪⎩；（2）12n =；（3）1-．【巩固训练】1．复数34i +的平方根是 ．例题解析【难度】★ 【答案】(2)i ±+2．计算：（11996= ． （2）151512(1)(1)(1)i -+=-+ ．【难度】★ 【答案】（1）12-；（2）03．已知ω满足等式210ωω++=．（1）计算4(1)ωω++；304050ωωω++；224(1)(1)ωωωω-+-+；（2）求证：对任意复数u ，有恒等式33233(1)()()3(1)u u u u ωω+++++=+； （3）计算：21n n ωω++，*n ∈N ． 【难度】★★【答案】（1）1-；0；4；（2）略；（3）*2**33()1031()032()n n n k k n k k n k k ωω⎧=∈⎪++==-∈⎨⎪=-∈⎩N N N2、复数中的代数式和方程【例5】在复数范围内分解因式：2223x x ++ 【难度】★【答案】22232x x x x ⎛++=-⎝⎭⎝⎭11222x x ⎛⎫⎛⎫-+=+- ⎪⎪ ⎪⎪⎝⎭⎝⎭【例6】复数z 满足方程210z z ++=，求()41z z ++的值 【难度】★★【答案】由210z z ++=得，21102z w z w w w ==-+=∴++=或 所以原式()()4428211w w ww w w w w =++=-+=+=+=-【巩固训练】1．若虚数z 满足327z =，则32315z z z +++的值为 ． 【难度】★★ 【答案】332．，，求的值.【难度】★★【答案】12ω=-时，原式=15-；12ω=-时，原式；3、实系数一元二次方程【例7】已知方程2350()x x m m -+=∈R ，求方程的解． 【难度】★【答案】920m ∆=- 当0∆>时，即920m <时，32x ±=；当0∆=时，即920m =时，32x =； 当0∆<时，即920m >时，32i x =．【例8】已知βα,是实系数一元二次方程02=++c bx ax 的两个虚根，且2αβ∈R ，求βα的值．【难度】★★【答案】∵2αβ∈R ，∴2222ααβαββαβ=⇒=，即330αβ-=∴12αβ=-± 1≠ω13=ω32302ωωω+++【例9】已知12,x x 是实系数方程20x x p ++=的两个根，且满足12||3x x -=，求实数p 的值． 【难度】★★ 【答案】14p ∆=-， （1）当0∆≥时，即14p ≤时，12,x x 是实根，∴12||3x x -==，即32p =⇒=-； （2）当0∆<时，即14p >时，12,x x 是共轭虚根，设1(,)x a bi a b =+∈R ，则2x a bi =-， ∴123|||2|2||32x x bi b b -===⇒=±，由1221x x a +==-，得12a =-．从而21215||2p x x x ===．综上，2p =-或52．【例10】已知,αβ是实系数一元二次方程230x mx -+=的两个根，求||||αβ+的值． 【难度】★★【答案】212m ∆=-，（1）当0∆≥时，即m ≥m ≤-30αβ=>，∴||||||||m αβαβ+=+=； （2）当0∆<时，即m -<<||||2||αβα+===．【例11】已知复数12,z z 满足1||2z =，2||1z =，12||2z z -=，求12z z ． 【难度】★★【答案】212121211121222||()()4z z z z z z z z z z z z z z -=--=⋅-⋅-⋅+⋅=， ∴12121z z z z ⋅+⋅=， ∴122211211z zz z z z z z ⋅⋅+⋅⋅=， ∴122141z zz z +=． 令12z t z =，则141t t+=，∴240t t -+=，∴122t =±，即12122z i z =±．【例12】（1）方程20()x px k p -+=∈R 有一个根为12i +，求实数k 的值； （2）方程240x x k -+=有一个根为12i +，求k 的值． 【难度】★【答案】（1）由题意：另一个根为12i -，∴(12)(12)5k i i =+-=； （2）由题意2(12)4(12)074i i k k i +-++=⇒=+．【例12】关于x 的方程2(2i)i 0x a b x a b --+-=有实根，且一个根的模是2，求实数a 、b 的值． 【难度】★★【答案】设()t t ∈R 是方程的一实根，则2(2)()i 0t at a bt b -++-=．则220,0t at a bt b ⎧-+=⎨-=⎩．（1）当0b =时，此方程为220x ax a -+=． ①有实根，0∆≥即1a ≥或0a ≤．当根为2时，440a a -+=．得43a =． 当根为2-时，440a a ++=．得45a =-．②有一对共轭虚根即01a <<．模为2，即有4a =（舍）．（2）当0b ≠时，则1t =，此时1a =．又因为模为2，所以b =所以4,30a b ⎧=⎪⎨⎪=⎩或4,50a b ⎧=-⎪⎨⎪=⎩或1,a b =⎧⎪⎨=⎪⎩1,a b =⎧⎪⎨=⎪⎩【巩固训练】1．下列命题在复数集中是否正确？为什么？（1）若,,a b c ∈R ，0a ≠，且240b ac -≥，则方程20ax bx c ++=有两个实数根；（2）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则12b x x a +=-，12cx x a=； （3）若,,a b c ∈R ，0a ≠，且12,x x 是方程20ax bx c ++=的两个根，则221212||()x x x x -=-；（4）若,,a b c ∈R ，0a ≠，且α是方程20ax bx c ++=的根，则α也是方程的根． 【难度】★★ 【答案】（1）、（2）、（4）正确，（3）不正确2．若12,x x 为方程270x x -+=的两个根，则212||x x -= ．【难度】★★ 【答案】273．已知,0x y ≠且，求20092009()(x y x y x y+++的值. 【难度】★★【答案】14．关于x 的方程222(31)10x m x m --++=的两根为αβ、，且||||3αβ+=，求实数m 的值． 【难度】★★【答案】53m =-或2m =5．设αβ、为方程220x x t ++=，（t ∈R ）的两个根，()||||f t αβ=+， （1）求()f t 的解析式；（2）证明关于t 的方程()f t m =，当2m >时恰有两个不等的根，且两根之和为定值． 【难度】★★【答案】（1）0()2,010t f t t t ⎧<⎪=<≤⎨⎪<⎩．．．（2）证明：函数()y f t =的图像关于直线12t =对称（证略） 当(1,)t ∈+∞时，()f t 为增函数，且()(2,)f t ∈+∞；022=++y xy x当(,0)t ∈-∞时，()f t 为减函数，且()(2,)f t ∈+∞．所以当2m >，方程()f t m =在区间(1,)+∞上有唯一解1t ，在区间(,0)-∞上也有唯一解2t ， 则121212t t +=⨯=．4、复数方程综合问题【例13】关于x 的二次方程2120x z x z m +++=中，1z ，2z ，m 都是复数，且21241620z z i -=+，设这个方程的两个根α、β满足||αβ-=||m 的最大值和最小值． 【难度】★★【答案】根据韦达定理有12z z mαβαβ+=-⎧⎨=+⎩∵22212()()444z z m αβαβαβ-=+-=-- ∴2212|()||4(4)|28m z z αβ-=--=．∴2121|(4)|74m z z --=，即|(45)|7m i -+=， 这表明复数m 在以(4,5)C 为圆心，7为半径的圆周上，∴max ||7m =min ||7m =当5001,150log 22m t m t >⎧⎪<<⎨<-⎪⎩即2log 215050m t -<<．【例14】已知22016220160122016(1)x x a a x a x a x ++=++++，试求0362016a a a a ++++的值。

公式法解一元二次方程的例题20道一元二次方程是中学数学学习中的重要内容，公式法是解一元二次方程的一种常见方法。

通过求根公式，可以解任意形式的一元二次方程，这在代数学习中具有重要意义。

接下来，我将结合公式法解一元二次方程的例题，带你一起深入理解这一知识点。

1. 解题思路在使用公式法解一元二次方程时，我们首先要将方程化为标准形式：$ax^2+bx+c=0$，然后利用求根公式：$$x=\frac{-b\pm\sqrt{b^2-4ac}}{2a}$$来求得方程的解。

在实际解题中，我们需要注意判别式$\Delta=b^2-4ac$的正负与零，以确定方程的解的个数及性质。

2. 例题1已知一元二次方程$2x^2-5x+2=0$，求方程的根。

解：根据公式法，首先计算判别式$\Delta=(-5)^2-4\times2\times2=1$，由于$\Delta>0$，则方程有两个不相等的实根。

代入求根公式，得$x_1=\frac{5+\sqrt{1}}{4}=\frac{7}{4}$，$x_2=\frac{5-\sqrt{1}}{4}=\frac{3}{2}$。

方程的解为$x_1=\frac{7}{4}$，$x_2=\frac{3}{2}$。

3. 例题2求一元二次方程$3x^2-4x+1=0$的根。

解：计算判别式$\Delta=(-4)^2-4\times3\times1=0$，由于$\Delta=0$，则方程有两个相等的实根。

代入求根公式，得$x_1=x_2=\frac{4}{6}=\frac{2}{3}$。

方程的解为$x_1=x_2=\frac{2}{3}$。

4. 例题3已知一元二次方程$4x^2-12x+9=0$，求方程的根。

解：计算判别式$\Delta=(-12)^2-4\times4\times9=-48$，由于$\Delta<0$，则方程没有实数根，只有一对共轭复数根。

代入求根公式，得$x_1=\frac{12+\sqrt{-48}}{8}=1+\frac{\sqrt{3}}{2}i$，$x_2=\frac{12-\sqrt{-48}}{8}=1-\frac{\sqrt{3}}{2}i$。

第3天一元二次方程的根与系数的关系与解决实际问题【知识回顾】1．根的判别式利用一元二次方程根的判别式（△＝b2﹣4ac）判断方程的根的情况．一元二次方程ax2+bx+c＝0（a≠0）的根与△＝b2﹣4ac有如下关系：△当△＞0时，方程有两个不相等的两个实数根；△当△＝0时，方程有两个相等的两个实数根；△当△＜0时，方程无实数根．上面的结论反过来也成立．2．根与系数的关系（1）若二次项系数为1，常用以下关系：x1，x2是方程x2+px+q＝0的两根时，x1+x2＝﹣p，x1x2＝q，反过来可得p＝﹣（x1+x2），q＝x1x2，前者是已知系数确定根的相关问题，后者是已知两根确定方程中未知系数．（2）若二次项系数不为1，则常用以下关系：x1，x2是一元二次方程ax2+bx+c＝0（a≠0）的两根时，12bx xa+=-，12cx xa⋅=．（3）常用根与系数的关系解决以下问题：△不解方程，判断两个数是不是一元二次方程的两个根．△已知方程及方程的一个根，求另1一个根及未知数．△不解方程求关于根的式子的值，如求，x12+x22等等．△判断两根的符号．△求作新方程．△由给出的两根满足的条件，确定字母的取值．这类问题比较综合，解题时除了利用根与系数的关系，同时还要考虑a≠0，△≥0这两个前提条件．3．由实际问题抽象出一元二次方程在解决实际问题时，要全面、系统地申清问题的已知和未知，以及它们之间的数量关系，找出并全面表示问题的相等关系，设出未知数，用方程表示出已知量与未知量之间的等量关系，即列出一元二次方程．一．选择题（共10小题）1．（2020·云南一模）若α、β是一元二次方程x2+2x﹣6＝0的两根，则11+αβ的值是（）A．13-B．13C．﹣3D．3【答案】B【解析】△α、β是一元二次方程x2+2x﹣6＝0的两根，△α+β＝﹣2，αβ＝﹣6，则11+-21 +===-63αβαβαβ，故选B．2．（2020·四川省射洪县射洪中学外国语实验学校期中）下列一元二次方程两实数根和为-42的是（）A．2240x x--=B．2440x x-+= C．24100x x++=D．2450x x-=+【答案】D【解析】A中1222 1x x -+=-=，故错误；B中12-44 1x x+=-=，故错误；C中24164024＜0b ac∆=-=-=-，故错误；D中124-4 1x x+=-=，故准确；故答案选D．3．（2020·四川省射洪县射洪中学外国语实验学校月考）方程22310m m-+=和方程224m m-=-所有实数根之和为（）A．72B．32C．32-D．92【答案】B【解析】34△方程22310m m -+=根的判别式2=(-3)42110∆-⨯⨯=＞△方程22310m m -+=有两个实数根△两根之和为32△方程224m m -=-的根的判别式2=(-2)414-120∆-⨯⨯=＜△方程224m m -=-无实数根△方程22310m m -+=和方程224m m -=-所有实数根之和为32故选：B 4．（2020·渠县第四中学期中）已知x 1，x 2是一元二次方程x 2－2x －1＝0的两根，则x 1＋x 2－x 1·x 2的值是（ ）A ．1B ．3C ．－1D ．－3 【答案】B【解析】由题意知：122x x +=，12-1x x ⋅=，△原式＝2－（－1）＝3故选B ．5．（2020·江苏如东二模）若x 1，x 2是方程x 2﹣3x ﹣2＝0的两个根，则x 1+x 2﹣x 1•x 2的值是（ ） A ．﹣5B ．﹣1C ．5D ．15【答案】C【解析】根据题意得x 1+x 2=3，x 1x 2=﹣2，所以x 1+x 2﹣x 1•x 2=3﹣(﹣2)=5．故选：C ．6．（2020·内蒙古海勃湾期末）一元二次方程2310x x -+=的两个根为12,x x ，则2121232x x x x ++-的值是（ ）A ．10B ．9C ．8D ．7【答案】D【解析】 1x 为一元二次方程2310x x -+=的根，21131x x ∴=-，2121232x x x x ∴++-=()12121212313233x x x x x x x x -++-=++-．根据题意得123x x +=，121=x x ，212123233137x x x x ∴++-=⨯+-=．故选：D ．7．（2020·银川市第十五中学一模）已知关于x 的方程x 2－4x ＋c ＋1＝0有两个相等的实数根，则常数c的值为( )A．－1B．3C．1D．0【答案】B【解析】△方程x2−4x+c+1=0有两个相等的实数根，△△=(−4)2−4(c+1)=12−4c=0，解得：c=3.故答案选B.8．（2019·广东郁南月考）某中学要组织一次篮球比赛，赛制为单循环形式（毎两队之间都赛一场），计划安排21场比赛，求参加的球队支数，如果设参加的球队支数为x，则可列方程为（）A．12x（x+1）=21B．x（x+1）=21C．12x（x﹣1）=21D．x（x﹣1）=21【答案】C【解析】解：设邀请x个队，每个队都要赛（x-1）场，但两队之间只有一场比赛，由题意得：12x（x-1）=21，故选：C．9．（2020·深圳市宝安区北亭实验学校）若一个三角形的两边长分别为2和6，第三边是方程x2－10x＋21＝0的一根，则这个三角形的周长为( )67A ．7B ．3或7C ．15D ．11或15【答案】C【解析】x 2−10x+21=0，(x−3)(x−7)=0，则x−3=0，x−7=0，解得：x=3或7， 当x=3时，2+3=5<6，不能组成三角形，故x=3不合题意舍去，当x=7时，2+6=8>7，可以组成三角形，则三角形的周长为2+6+7=15，故答案选C.10．（2020·湖南隆回一模）扬帆中学有一块长30m ，宽20m 的矩形空地，计划在这块空地上划出四分之一的区域种花，小禹同学设计方案如图所示，求花带的宽度．设花带的宽度为xm ，则可列方程为（ ）A ．()()3302020304x x --=⨯⨯B ．()()130********x x --=⨯⨯8C ．130********x x +⨯=⨯⨯ D ．()()33022020304x x --=⨯⨯ 【答案】D【解析】 设花带的宽度为xm ，则可列方程为330220203(4())0x x --=⨯⨯， 故选D ．二．填空题（共5小题） 11．（2020·江苏高淳期末）一元二次方程x 2+mx+2m=0的两个实根分别为x 1，x 2，若x 1+x 2=1，则x 1x 2=______.【答案】-2．【解析】根据题意得x 1+x 2=-m=1，x 1x 2=2m ，所以m=-1，所以x 1x 2=-2．12．（2020·温州市第二十三中学）已知关于x 的方程260x x a ++=有一个根是-2，则方程的另一个根是___________．【答案】-4【解析】因为已知关于x 的方程260x x a ++=有一个根是-2，9 所以由12b x x a+=-得2226,4x x -+=-∴=-． 故答案为-4． 13．（2020·四川省射洪县射洪中学外国语实验学校期中）若,a b 是方程2220060x x +-=的两根，则23a a b ++= ．【答案】2004．【解析】2220060x x +-=的两根△a+b=-2，222006a a +=，△223=2+a =2006-2=2004++++a a b a a b故答案为：200414．（2020·四川省射洪县射洪中学外国语实验学校期中）如果关于x 的一元二次方程()20ax b ab =>的两个根分别是11x m =+与224x m =-，那么b a的值为__________. 【答案】4【解析】方程化为一般式为：ax 2-b=0x 1+x 2=m+1+2m -4=0 △x 1·x 2=（m+1）（2m -4）=-b a △10解方程△，得m=1把m=1代入△，得b a=-2×（-2）=4. 故答案为：4.15．（2019·上海交大附中）设方程( 1) (11)(11)(21)x x x x ++++++(1)(21)0x x ++=的两根为12,x x ，则()()1211x x ++=______． 【答案】2003【解析】(1)(11)(11)(21)1)(20(1)x x x x x x ++++++++=， 221211x x x ∴++++23223122210x x x ++++=， 23662630x x ∴++=．△3a =，66b =，263c =，224664326343563156b ac ∆=-=-⨯⨯=-=12000>， 1212263223x x b a a x c x =-=∴+=-=，． ()()()1212122631112213x x x x x x ++=+++=-+=2003． 故答案为：2003． 三．解析题（共5小题）1116．（2019·广东郁南月考）关于x 的方程x 2﹣2（k ﹣1）x +k 2＝0有两个实数根x 1、x 2． （1）求k 的取值范围；（2）若x 1+x 2＝1﹣x 1x 2，求k 的值．【答案】（1）12k ≤；（2）3k = 【解析】(1)△Δ＝4(k －1)2－4k 2≥0，△－8k ＋4≥0，△k ≤12； (2)△x 1＋x 2＝2(k －1)，x 1x 2＝k 2，△2(k －1)＝1－k 2，△k 1＝1，k 2＝－3.△k ≤12，△k ＝－3. 17．（2020·甘肃省庆阳市第五中学期末）已知关于x 的一元二次方程()222120x k x k k -+++=有两个实数根12,x x ．（1）求实数k 的取值范围．（2）是否存在实数k ，使得()22121216x x x x +-=成立？若存在，请求出k 的值；若不存在，请说明理由．【答案】（1）14k ≤；（2）存在这样的实数k ，k 的值为3-． 【解析】（1）由题意得：方程的根的判别式[]22(21)4(2)0k k k ∆=-+-+≥，12 解得14k ≤； （2）由一元二次方程根与系数的关系得：2121221,2x x k x x k k +=+=+，则()()2222121211221223x x x x x x x x x x +-=++-， ()212123x x x x =+-， ()()222132k k k =+-+， 221k k =-+，当()22121216x x x x +-=时，22116k k -+=， 即22150k k --=，因式分解得：(3)(5)0k k +-=，解得3k =-或154k =>（不符题意，舍去）， 故存在这样的实数k ，k 的值为3-．18．（2020·四川南充月考）关于x 的方程2220x mx m m -+-=有两个不相等的实数根12,x x .（1）求m 的取值范围.（2）若221212x x +=，求211214x x x x +-的值.13【答案】（1）0m >；（3）0【解析】（1）△1a =，2b m =-，2c m m =-，△()()2224241b ac m m m =-=--⨯⨯- 40m =>△0m >；（2）由根与系数的关系，得：212122x x m x x m m +==-，，△221212x x +=，△()21212212x x x x +-=，△()224212m m m --=， △2+60m m -=，解得2m =或3m =-（舍去），△原方程为2420x x -+=，△212112420x x x x =-+=，，△211214220x x x x +-=-+=．19．（2020·湖南茶陵期末）已知关于x 的一元二次方程240x x m -+=．14（1）若方程有实数根，求实数m 的取值范围；（2）若方程的两个实根为12,x x ，且满足12326x x +=，求实数m 的值．【答案】（1）4m ≤；（2）12=-m ．【解析】（1）△原方程有实数根，△方程的根的判别式1640m ∆=-≥，解得4m ≤；（2）由一元二次方程的根与系数的关系得：12441x x -+=-=， 又121211322()246x x x x x x +=++=⨯+=，12x ∴=-，将12x =-代入原方程得：2(2)4(2)0m --⨯-+=，解得12=-m ．20．（2020·渠县第四中学期中）某商场试销一件成本为60元的服装，规定试销期间销售单价不低于成本单价，经试销发现，销售量y(件)与销售单价x(元)符合一次函数y ＝kx ＋b ，且x ＝65时，y ＝55；x ＝75时，y ＝45．(1)求y 与x 的函数关系式；(2)若该商场想获得利润500元，求销售单价．【答案】（1）y ＝－x ＋120(60≤x≤120)；（2）销售单价为70元或110元．【解析】解：(1)根据题意，得6555 7545k bk b+=⎧⎨+=⎩解得1120 kb=-⎧⎨=⎩△一次函数关系式为y＝－x＋120(60≤x≤120)．(2)(－x＋120)(x－60)＝500，整理得x2－180x＋7700＝0．解得x1＝70，x2＝110，答：当销售单价为70元或110元时，该商场获得500元利润．15。

一元二次方程的解法汇总1．直接开方法解一元二次方程(1)直接开方法解一元二次方程：利用平方根的定义直接开平方求一元二次方程的解的方法称为直接开平方法.(2)直接开平方法的理论依据：平方根的定义.(3)能用直接开平方法解一元二次方程的类型有两类：（点击图片可放大阅览）要点诠释：用直接开平方法解一元二次方程的理论依据是平方根的定义，应用时应把方程化成左边是含未知数的完全平方式，右边是非负数的形式，就可以直接开平方求这个方程的根.2.因式分解法解一元二次方程（1）用因式分解法解一元二次方程的步骤:①将方程右边化为0；②将方程左边分解为两个一次式的积；③令这两个一次式分别为0，得到两个一元一次方程；④解这两个一元一次方程，它们的解就是原方程的解.（2）常用的因式分解法提取公因式法，公式法（平方差公式、完全平方公式），十字相乘法等.要点诠释：（1）能用分解因式法来解一元二次方程的结构特点：方程的一边是0，另一边可以分解成两个一次因式的积；（2）用分解因式法解一元二次方程的理论依据：两个因式的积为0，那么这两个因式中至少有一个等于0；（3）用分解因式法解一元二次方程的注意点：①必须将方程的右边化为0；②方程两边不能同时除以含有未知数的代数式.【典型例题】类型一、用直接开平方法解一元二次方程（点击图片可放大阅览）【总结升华】应当注意，如果把x+m看作一个整体，那么形如(x+m)2=n(n≥0)的方程就可看作形如x2=k的方程，也就是可用直接开平方法求解的方程；这就是说，一个方程如果可以变形为这个形式，就可用直接开平方法求出这个方程的根．所以，(x+m)2=n可成为任何一元二次方程变形的目标．举一反三：（点击图片可放大阅览）类型二、因式分解法解一元二次方程（点击图片可放大阅览）【总结升华】若把各项展开，整理为一元二次方程的一般形式，过程太烦琐．观察题目结构，可将x+1看作m，将(2-x)看作n，则原方程左端恰好为完全平方式，于是此方程利用分解因式法可解．举一反三：【变式】方程(x-1)(x+2)＝2(x+2)的根是________．【答案】将(x+2)看作一个整体，右边的2(x+2)移到方程的左边也可用提取公因式法因式分解．即(x-1)(x+2)-2(x+2)＝0，(x+2)[(x-1)-2]＝0．∴ (x+2)(x-3)＝0，∴ x+2＝0或x-3＝0．∴ x1＝-2 x2＝3．（点击图片可放大阅览）【总结升华】如果把视为一个整体，则已知条件可以转化成一个一元二次方程的形式，用因式分解法可以解这个一元二次方程．此题看似求x、y 的值，然后计算，但实际上如果把看成一个整体，那么原方程便可化简求解。

一元二次方程两个解的公式一元二次方程是高中数学中的重要内容，解一元二次方程的方法有很多，其中最常用的就是求解一元二次方程的两个解的公式。

这个公式被广泛使用，可以用来求解各种实际问题，如物理、工程等领域中的应用问题。

本文将详细介绍一元二次方程两个解的公式及其应用。

一元二次方程的一般形式为：ax^2 + bx + c = 0，其中a、b、c 为已知系数，x为未知数。

为了求解这个方程，我们可以使用求根公式。

一元二次方程的两个解的公式为：x = (-b ± √(b^2 - 4ac)) / 2a。

这个公式中，±表示两个解，√表示求平方根，b^2 - 4ac被称为判别式。

判别式的值决定了方程的解的性质。

我们来讨论判别式的值对方程解的影响。

当判别式大于0时，方程有两个不相等的实数解；当判别式等于0时，方程有两个相等的实数解；当判别式小于0时，方程没有实数解，但有两个共轭复数解。

接下来，我们通过几个例子来说明一元二次方程两个解的求解过程。

例子1：解方程x^2 - 4x + 3 = 0根据一元二次方程两个解的公式，我们可以得到解的表达式为：x = (4 ± √(4^2 - 4×1×3)) / 2×1。

计算判别式的值：b^2 - 4ac = 4^2 - 4×1×3 = 16 - 12 = 4。

判别式大于0，所以方程有两个不相等的实数解。

代入公式进行计算：x1 = (4 + √4) / 2 = (4 + 2) / 2 = 3， x2 = (4 - √4) / 2 = (4 - 2) / 2 = 1。

所以，方程x^2 - 4x + 3 = 0的解为x1 = 3，x2 = 1。

例子2：解方程2x^2 + 4x + 2 = 0根据一元二次方程两个解的公式，我们可以得到解的表达式为：x = (-4 ± √(4^2 - 4×2×2)) / 2×2。

高中一元二次方程的解法如下：1. 直接开平方法：如果一元二次方程的二次项系数为a，一次项系数为b，常数项为c，且a≠0，那么x^2=b/a，那么这样的方程就可以通过直接开平方的方法解出其解。

2. 配方法：把一元二次方程配成(x+m)^2=n的形式，再利用直接开平方法求解，这样可以使计算简化。

3. 因式分解法：利用乘法公式来分解因式，通过因式分解来求解一元二次方程。

首先要通过观察或分析，确定一元二次方程的最高项和一次项的分母为1时可能有几个因式在x^2±2bx+c=0；或b^2-4ac≥0时可用公式求得解。

下面我们以一些例题的形式展示这些解法：例1：（1）方程x^2-4x+3=0；（2）方程（x-1）^2-2（x-1）+2=0；解：（1）由原方程，得（x-1.5）^2-2.25=0。

直接开平方得：x-1.5=±1.5，所以x?=3，x?=0；（2）由原方程，得（x-1-1）^2=0，所以x?=x?=2。

例2：用因式分解法解方程：x^2-3x+2=0。

解：原式=（x-1）（x-2）=0，得x?=1，x?=2。

除了上述两种方法外，还有公式法等其他解法。

公式法需要用到一元二次方程的求根公式，通过使用根公式来解一元二次方程。

具体步骤包括将一元二次方程化为一般形式，确定判别式的值，根据判别式的值确定根的个数，然后使用根的公式求出方程的根。

总结：高中一元二次方程的解法包括直接开平方法、配方法、因式分解法和公式法等。

选择哪种方法取决于方程的特点和需要，有时候可能需要多种方法联合使用来解决问题。

理解和掌握这些解法对于解决一元二次方程问题非常重要。

另外需要注意的是，在实际应用中，一元二次方程往往需要通过数学模型建立、数据处理和分析等方法进行求解。

这就需要结合实际问题和数学知识进行综合应用和创新思考。

一元二次方程配方法公式一元二次方程是我们在学习数学的过程中经常遇到的一个重要内容，它在数学中有着广泛的应用。

解一元二次方程的方法有很多种，其中配方法是一种常用且有效的解法。

本文将介绍一元二次方程配方法的公式及其应用。

首先，我们来回顾一下一元二次方程的一般形式，ax^2 + bx + c = 0，其中a、b、c分别为方程的系数，x为未知数。

解一元二次方程的一般步骤是先利用配方法将方程化为完全平方的形式，然后再进行求解。

下面我们将详细介绍一元二次方程配方法的公式及其应用。

一元二次方程配方法的公式如下：1. 将方程化为完全平方的形式，ax^2 + bx + c = a(x^2 + (b/a)x) + c = a[(x +b/(2a))^2 (b/(2a))^2] + c。

2. 化简方程，ax^2 + bx + c = a(x + b/(2a))^2 (b^2 4ac)/(4a)。

3. 令u = x + b/(2a)，则方程化为，au^2 (b^2 4ac)/(4a) + c = 0。

通过以上公式，我们可以将一元二次方程化为完全平方的形式，从而更容易求解。

接下来，我们将通过一个具体的例子来演示一元二次方程配方法的应用。

例题，解方程x^2 + 6x + 9 = 0。

解：首先，根据配方法的公式，我们可以将方程化为完全平方的形式：x^2 + 6x + 9 = (x + 3)^2。

因此，方程化为，(x + 3)^2 = 0。

接着，我们可以通过开平方的方法求解方程：x + 3 = 0。

x = -3。

所以，方程x^2 + 6x + 9 = 0的解为x = -3。

通过以上例子，我们可以看到一元二次方程配方法的应用非常简便，通过将方程化为完全平方的形式，我们可以更加直观地求解方程，避免了繁琐的计算过程。

总结一元二次方程配方法的公式及其应用，可以帮助我们更好地理解和掌握解一元二次方程的方法。

在实际问题中，我们可以通过配方法来快速求解一元二次方程，为数学建模和实际应用提供了便利。

新教材高中数学教师用书：第2课时 复数的除法及实系数一元二次方程在复数范围内的解集[课程目标] 1.掌握复数的除法法则，并能运用复数的除法法则进行计算.2.会在复数范围内解实系数一元二次方程．知识点一 复数的除法[填一填](1)复数的除法如果复数z 2≠0，则满足zz 2＝z 1的复数z 称为z 1除以z 2的商，并记作z ＝z 1z 2(或z ＝z 1÷z 2)，z 1称为被除数，z 2称为除数．(2)复数的倒数给定复数z ≠0，称1z 为z 的倒数，z 1除以z 2的商z 1z 2也可以看成z 1与z 2的倒数之积．(3)运算法则(a ＋b i)÷(c ＋d i)＝a ＋b ic ＋d i ＝(a ＋b i)(1c ＋d i )＝(a ＋b i)·c －d ic 2＋d2＝ac ＋bd ＋bc －ad i c 2＋d 2＝ac ＋bd c 2＋d 2＋bc －adc 2＋d2i.[答一答]怎样理解和应用复数代数形式的除法法则？提示：(1)复数代数形式的除法是复数代数形式的乘法的逆运算． (2)复数除法的运算法则不必死记，在实际运算时，只需把商a ＋b ic ＋d i看作分数，分子、分母同乘以分母的共轭复数c －d i ，把分母变为实数，化简后，就可以得到运算结果． 知识点二 实系数一元二次方程[填一填]当a ，b ，c 都是实数且a ≠0时，关于x 的方程ax 2＋bx ＋c ＝0称为实系数一元二次方程，这个方程在复数范围内总是有解的，而且(1)当Δ＝b 2－4ac >0时，方程有两个不相等的实数根； (2)当Δ＝b 2－4ac ＝0时，方程有两个相等的实数根； (3)当Δ＝b 2－4ac <0时，方程有两个互为共轭的虚数根．复数的模的运算性质．设z ＝a ＋b i(a ，b ∈R )，|z |＝a 2＋b 2， (1)|z |＝|z －|；(2)|z 1·z 2|＝|z 1|·|z 2|；(3)|z 1z 2|＝|z 1||z 2|(z 2≠0)；(4)|z n|＝|z |n； (5)|z |＝1⇔z ·z －＝1；(6)|z |2＝|z －|2＝|z 2|＝|z －2|＝z ·z －.类型一 复数的除法运算[例1] 计算下列各式： (1)1－4i 1＋i ＋2＋4i3＋4i ；(2)i －2i －11＋ii －1＋i.[分析] 题中既有加、减、乘、除运算，又有括号，同实数的运算顺序一致，先算括号里的，再算乘除，最后算加减．[解] (1)1－4i1＋i ＋2＋4i3＋4i＝1＋4＋－4＋1i ＋2＋4i 3＋4i ＝7＋i3＋4i＝7＋i3－4i 3＋4i 3－4i ＝21＋4＋3－28i 25＝25－25i25＝1－i. (2)i －2i －11＋ii －1＋i ＝－1－i －2i ＋2i －1－1－i ＋i ＝1－3i－2＋i＝1－3i －2－i －2＋i －2－i ＝－2－3＋6－1i5＝－5＋5i5＝－1＋i.复数的运算顺序与实数运算顺序相同，都是先进行高级运算乘方、开方，再进行次级运算乘、除，最后进行低级运算加、减.如i 的幂运算，先利用i 的幂的周期性，将其次数降低，然后再进行四则运算.[变式训练1] 计算：(1)2－i 3－4i 1＋i2＋(1－i)2；(2)i －231＋23i ＋(5＋i 3)－(1＋i 2)6.解：(1)2－i3－4i 1＋i2＋(1－i)2＝2－i 3－4i ·2i －2i ＝2－i 8＋6i －2i ＝2－i8－6i8＋6i8－6i－2i＝10－20i 100－2i ＝110－115i.(2)i －231＋23i ＋(5＋i 3)－(1＋i 2)6＝1＋23ii 1＋23i ＋(5＋i 2·i)－[(1＋i 2)2]3＝i ＋5－i －i 3＝5＋i.类型二 实系数一元二次方程的解集[例2] 求下列一元二次方程的解： (1)3x 2＋5x ＋1＝0； (2)2x 2－3x ＋3＝0； (3)4x 2－5x ＋2＝0.[分析] 求一元二次方程的根，最实用的方法是用求根公式法，如果Δ>0，则在实数系中有解，若Δ<0，则在复数系中有解.[解] (1)Δ＝52－4×3×1＝13， 故x ＝－5±132×3＝－5±136.(2)Δ＝(－3)2－4×2×3＝－15，故x ＝3±15i 2×2＝3±15i 4.(3)Δ＝(－5)2－4×4×2＝－7， 故x ＝5±7i 2×4＝5±7i8.在解一元二次方程的解时，要注意Δ的符号.[变式训练2] 已知关于x 的方程x 2－2ax ＋a 2－4a ＋4＝0(a ∈R )的两根为α、β，且|α|＋|β|＝3，求实数a 的值．解：由已知有Δ＝(－2a )2－4(a 2－4a ＋4)＝16a －16. ①当Δ≥0即a ≥1时，由⎩⎪⎨⎪⎧α＋β＝2a >0，αβ＝a －22≥0可知两根都是非负实根，∴|α|＋|β|＝α＋β＝3＝2a ⇒a ＝32；②当Δ<0即a <1时，此时方程两根为共轭虚根， 设α＝m ＋n i ，则β＝m －n i.∴⎩⎪⎨⎪⎧α＋β＝2m ＝2a ，αβ＝m 2＋n 2＝a －22.∴|α|＋|β|＝2m 2＋n 2＝2|a －2|＝3⇒a ＝12；综上，a ＝32或12.类型三 复数运算的综合应用[例3] 设z 是虚数，ω＝z ＋1z是实数，且－1<ω<2.(1)求|z |的值及z 的实部的取值范围； (2)设u ＝1－z1＋z ，求证：u 为纯虚数；(3)求ω－u 2的最小值．[分析] (1)ω是实数可得到哪些结论？(ω的虚部为0或ω＝ω)(2)u 为纯虚数可得到哪些结论？(u 的实部为0且虚部不为0，或u ＝－u )[解] (1)∵z 是虚数，∴可设z ＝x ＋y i ，x ，y ∈R ，且y ≠0.∴ω＝z ＋1z ＝x ＋y i ＋1x ＋y i＝x ＋y i ＋x －y i x 2＋y 2＝x ＋x x 2＋y 2＋(y －yx 2＋y 2)i. ∵ω是实数，且y ≠0，∴y －yx 2＋y 2＝0，∴x 2＋y 2＝1，即|z |＝1.此时ω＝2x . ∵－1<ω<2，∴－1<2x <2，从而有－12<x <1.即z 的实部的取值范围是(－12，1)．(2)证明：u ＝1－z 1＋z ＝1－x ＋y i1＋x ＋y i＝1－x －y i1＋x －y i 1＋x2＋y 2＝1－x 2－y 2－2y i1＋x 2＋y2＝－y1＋xi.∵x ∈(－12，1)，y ≠0，∴y1＋x ≠0.∴u 为纯虚数．(3)ω－u 2＝2x －(－y1＋x i)2＝2x ＋(y1＋x )2＝2x ＋1－x21＋x 2＝2x ＋1－x 1＋x ＝2x －1＋21＋x＝2(x ＋1)＋21＋x－3. ∵－12<x <1，∴1＋x >0.于是ω－u 2＝2(x ＋1)＋21＋x－3≥22x ＋1·21＋x－3＝1. 当且仅当2(x ＋1)＝21＋x ，即x ＝0时等号成立．∴ω－u 2的最小值为1，此时z ＝±i.该题涉及复数的基本概念和四则运算以及均值不等式等知识.只要概念清楚，运算熟练，按常规思路顺其自然不难求解.注意：解决后面的问题时，可以使用前面已经得到的结论.[变式训练3] 设z 2＝8＋6i ，求z 3－16z －100z.解：z 3－16z －100z ＝z 4－16z 2－100z＝z 2－82－164z＝6i2－164z ＝－200z ＝－200zz ·z＝－200z |z |2.∵|z |2＝|z 2|＝|8＋6i|＝10，又由z 2＝8＋6i ，得z ＝±(3＋i)，∴z ＝±(3－i)， ∴原式＝－200z|z |2＝－60＋20i 或60－20i.1．已知a 为正实数，i 为虚数单位，若a ＋ii的模为2，则a ＝( B ) A ．2 B. 3 C. 2 D ．1解析：因为a ＋ii＝1－a i ，所以1＋a 2＝2，又a >0，故a ＝3，故选B.2．在复平面内，复数10i3＋i 对应的点的坐标为( A )A ．(1,3)B ．(3,1)C ．(－1,3)D ．(3，－1) 解析：本题考查复数的乘法与除法． 10i3＋i＝10i 3－i 3＋i 3－i ＝10＋30i10＝1＋3i.∴复数10i3＋i对应的点的坐标为(1,3)．3．复数z 满足(z －i)(2－i)＝5，则z ＝( D ) A ．－2－2i B ．－2＋2i C ．2－2iD ．2＋2i解析：由题意可得，z －i ＝52－i ＝52＋i2－i 2＋i ＝2＋i ，所以z ＝2＋2i. 4．若x ，y ∈R ，且x1－i －y 1－2i ＝51－3i，则x ＝－1，y ＝－5. 解析：∵x 1－i －y 1－2i ＝51－3i，∴x 1－2i －y 1－i1－i1－2i＝51＋3i 1－3i 1＋3i ，∴x －y ＋y －2x i －1－3i＝1＋3i2，∴(x －y )＋(y －2x )i ＝－1＋3i22＝4－3i ，∴⎩⎪⎨⎪⎧x －y ＝4，y －2x ＝－3，解得⎩⎪⎨⎪⎧x ＝－1，y ＝－5.。

初中数学-二元一次方程和一元二次方程详解我选择介绍初中数学中的二元一次方程和一元二次方程的基本概念和解法。

一、二元一次方程二元一次方程是形如ax+by=c的方程，其中a,b,c为已知系数，x,y为未知数，且a,b不同时为0。

二元一次方程可以通过联立两个方程组成，例如：2x+y=53x-2y=8将这两个方程进行联立，可以得到：2x+y=5-6x+4y=-16然后我们采用消元法即可：将第二个方程乘以1/2，得到：2x+y=5-3x+2y=-8然后我们将第二个方程中的y消去，得到：2x+y=5-3x+2y=-8===================7x=-15因此，x=-15/7。

将x的值代回到第一个方程式中，可以解得y=25/7。

因此，原方程组的解为(x,y)=(-15/7,25/7)。

二、一元二次方程一元二次方程是形如ax²+bx+c=0的方程，其中a,b,c为已知系数，x为未知数，且a≠0。

求解一元二次方程通常有三种方法：配方法、公式法和图像法。

1）配方法：通过将方程式拆分成两个平方形式的式子，进而进行配方运算，最终得到方程的解。

例如，对于方程x²+6x+8=0，可以将其化为(x+2)(x+4)=0的形式，从而解得x=-2或x=-4。

2）公式法：对于形如ax²+bx+c=0的一元二次方程，可以使用求根公式：x = (-b ± √b²-4ac) / 2a来解方程。

其中，±表示两个解，√表示根号。

需要注意的是，一元二次方程的根数量可能为0、1或2个，具体取决于方程的判别式：b²-4ac。

3）图像法：将一元二次方程表示为y=ax²+bx+c的形式，可以得到一条开口朝上或朝下的抛物线。

通过观察或绘制这个抛物线，可以得到方程的解。

例如，对于方程x²-4x+3=0，我们可以将其表示为y=x²-4x+3的形式。

一元二次方程二次函数一元二次不等式知识归纳一元二次方程、二次函数和一元二次不等式知识归纳一元二次方程、二次函数和一元二次不等式是高中数学中的重要内容，掌握了这些知识可以帮助我们解决实际问题和推导数学关系。

本文将对一元二次方程、二次函数和一元二次不等式进行归纳总结，以帮助读者更好地理解和掌握这些知识。

一、一元二次方程一元二次方程是形如ax^2 + bx + c = 0（其中a ≠ 0）的方程，其中x 表示未知数。

解一元二次方程的常用方法有因式分解法、配方法和求根公式法。

1. 因式分解法当一元二次方程可以因式分解为两个一次因子相乘时，我们可以通过将方程两边置零，将每个因子等于零来求解。

例如，对于方程x^2 -5x + 6 = 0，我们可以将其因式分解为(x - 2)(x - 3) = 0，从而得到x = 2和x = 3两个解。

2. 配方法当一元二次方程无法直接因式分解时，我们可以通过配方法将方程转化为完全平方式，然后再进行求解。

例如，对于方程x^2 - 5x + 6 = 0，我们可以通过将常数项进行拆分，得到x^2 - 2x - 3x + 6 = 0，进而变为(x(x - 2) - 3(x - 2) = 0，再经过合并同类项和提取公因式的步骤得到(x -2)(x - 3) = 0，进而求得x = 2和x = 3两个解。

3. 求根公式法对于一元二次方程ax^2 + bx + c = 0，我们可以通过求根公式x = (-b ± √(b^2 - 4ac)) / (2a)来求解。

其中，±表示两个相反的解，而√表示平方根。

这种方法适用于所有一元二次方程的求解，包括没有实数解的情况。

二、二次函数二次函数是形如f(x) = ax^2 + bx + c的函数，其中a、b、c是实数且a ≠ 0。

二次函数的图像通常是一个开口朝上或朝下的抛物线。

掌握了二次函数的性质和图像特点可以帮助我们分析函数的变化趋势和解决实际问题。

已知实系数一元二次方程
已知实系数的一元二次方程是指形式为ax²+bx+c=0的方程，其中a、b、c都是实数且a≠0。

其中，a、b、c分别代表二次项、一次项和常数项的系数。

在求解这样的方程时，常用的方法有配方法、公式法和图解法等。

配方法是指通过变形，将一元二次方程转化成平方差或完全平方的形式，从而求解方程。

公式法则是指利用一元二次方程的求根公式：x=(-b±√(b²-4ac))/(2a)，求解方程的根。

图解法是指通过绘制方程的图像，找到方程的根。

根据判别式Δ=b²-4ac的值，我们可以判断一元二次方程有1个、2个或0个实数根。

用求根公式法解一元二次方程一元二次方程是数学中常见的一类方程，它的一般形式为ax^2+bx+c=0，其中a、b、c为已知常数，x为未知数。

求解一元二次方程的方法有很多，其中一种常用的方法是求根公式法。

求根公式法是通过使用一元二次方程的根的公式来求解方程。

一元二次方程的根的公式如下：x = (-b±√(b^2-4ac))/(2a)其中，±表示两个解，一个为加号，一个为减号。

根据这个公式，我们可以计算出一元二次方程的解。

下面我们通过一个具体的例子来说明求根公式法的应用。

例题：解方程x^2-5x+6=0解：首先，我们将方程的系数代入根的公式中，得到：x = (5±√((-5)^2-4*1*6))/(2*1)化简得：x = (5±√(25-24))/2继续化简得：x = (5±√1)/2由于√1=1，所以我们可以得到：x1 = (5+1)/2 = 3x2 = (5-1)/2 = 2因此，方程x^2-5x+6=0的解为x1=3和x2=2。

通过这个例子，我们可以看到求根公式法的求解过程。

首先，我们将方程的系数代入根的公式中，然后化简得到最终的解。

这种方法简单直接，适用于所有的一元二次方程。

需要注意的是，当方程的判别式b^2-4ac小于0时，方程没有实数解，此时方程的解为虚数解。

此时，我们可以通过计算出的根的实部和虚部得到方程的解。

求根公式法是解一元二次方程的常用方法之一，它的原理简单清晰，适用范围广泛。

在实际问题中，我们经常需要求解一元二次方程，求根公式法可以帮助我们快速准确地求解方程的解。

除了求根公式法外，还有其他方法可以用来解一元二次方程，比如配方法、因式分解法等。

每种方法都有其特点和适用范围，我们可以根据具体情况选择合适的方法来求解方程。

求根公式法是解一元二次方程的一种简单有效的方法。

通过代入方程的系数，利用根的公式进行计算，可以得到方程的解。

在实际应用中，我们可以根据具体问题选择合适的求解方法，以便更好地解决问题。

小学数学认识一元二次方程一元二次方程是小学数学中较为复杂的一个概念，需要对数学概念有一定的了解才能理解和解决。

一元二次方程包含一个未知数和其次方的方程，通常写作ax^2 + bx + c = 0，其中a、b、c为已知系数，a不等于0。

本文将介绍一元二次方程的基本概念、解法以及应用。

一、基本概念在学习一元二次方程之前，我们需要了解一些基本概念。

1.1 平方数：一个数的平方，例如1、4、9、16等。

1.2 二次方程：方程中含有未知数的平方项的方程，例如x^2 + 2x + 1 = 0就是一个二次方程。

1.3 一元二次方程：方程中只有一个未知数的平方项的方程，例如3x^2 - 2x + 1 = 0就是一个一元二次方程。

二、解法解一元二次方程通常有以下两种方法：因式分解法和求根公式法。

2.1 因式分解法：对于一些特殊的一元二次方程，可以通过因式分解的方法得到方程的解。

例如，对于方程x^2 - 4x + 3 = 0，我们可以将其分解为(x - 3)(x - 1) = 0，从而得到x的解为x = 3或x = 1。

2.2 求根公式法：对于一般的一元二次方程，我们可以使用求根公式来求解。

求根公式为x = (-b ± √(b^2 - 4ac)) / (2a)。

例如，对于方程2x^2 + 5x + 2 = 0，我们可以代入a = 2，b = 5，c = 2，然后计算得到x的解为x = -1/2或x = -2。

三、应用一元二次方程在现实生活中有着广泛的应用。

3.1 抛物线运动：抛出的物体在空中的运动轨迹可以用一元二次方程来表示。

例如，投掷一颗子弹的运动轨迹可以表示成y = -5x^2 + 10x + 3的形式，其中y为高度，x为时间。

3.2 建模和预测：一元二次方程可以用来对一些现实问题进行建模和预测。

例如，根据某商品的销售数据，可以建立销售量和价格之间的一元二次方程，从而预测不同价格下的销售量。

3.3 几何问题：一元二次方程也可以用来解决几何问题。