第5章随机信号分析

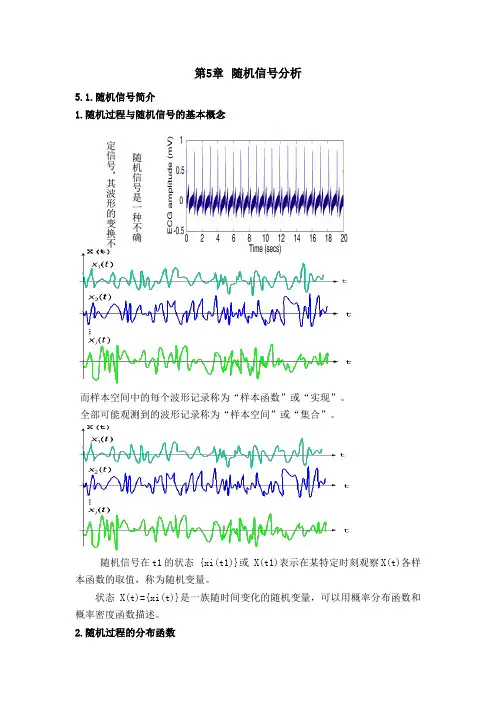
第5章 随机信号分析5.1.随机信号简介1.随机过程与随机信号的基本概念而样本空间中的每个波形记录称为“样本函数”或“实现”。

全部可能观测到的波形记录称为“样本空间”或“集合”。

随机信号在t1的状态 {xi(t1)}或 X(t1)表示在某特定时刻观察X(t)各样本函数的取值，称为随机变量。

状态X(t)={xi(t)}是一族随时间变化的随机变量，可以用概率分布函数和概率密度函数描述。

2.随机过程的分布函数随机信号是一种不确定信号，其波形的变换不存在。

任何确定的规律。

因而无法准确预测未来值{X[k], k ∈Z}表示一个随机过程一维分布函数 )][();(x k X P k x F ≤=二维分布函数 )][,][(),;,(22112121x k X x k X P k k x x F ≤≤= 三维分布函数 ),,;,,,(2121N N k k k x x x F)][,][(11N N x k X x k X P ≤≤=3.随机信号的数字特征均值 ]}[{][k X E k m x =方差 ]}[][{}])[][{(][2222k m k X E k m k X E k x x x-=-=σ 自相关函数 ]}[][{],[2121k X k X E k k R x =互相关函数 ]}[][{],[2121k Y k X E k k R xy = 4.平稳各态遍历随机信号的时域描述 （1） 平稳随机序列指统计特性不随时间的平移而变化的那一类随机序列 严平稳随机序列：),,;,,,(),,;,,,(21212121n k n k n k x x x F k k k x x x F N N N N +++=宽平稳随机序列：x m k X E =]}[{ ][]}[][{n R n k X k X E x =+平稳随机信号自相关函数特性：1）对称性 ][][n R n R x x -=2）极限值 0=n ]}[{]0[2k X E R x =∞→n 2][xx m R =∞ 3）不等式 ][]0[n R R x x ≥（2）各态遍历随机信号:时间平均等于统计平均 ∑-=∞→+==NNk N xk x N k X E m ][121lim ]}[{ ∑-=∞→-+=-=NNk x N x xm k x N m k X E 222]][[121lim }]][{[σ][][121lim ]}[][{][n k x k x N n k X k X E n R NNk N x ++=+==∑-=∞→ 5.平稳各态遍历随机信号的频域描述 随机信号的平均功率定义为][121lim 2k x N P NNk N x ∑-=∞→+= 对平稳、各态遍历的随机过程上式可写为]0[x x R P = 随机信号的功率谱定义为(维纳—辛钦定理)]}[{DTFT )(n R P x x =Ω由IDTFT 可得：ΩΩ==⎰-d )(π21]0[ππx x x P P R5.2、经典功率谱估计1.谱估计的质量估计量的偏差 θθθ-=}ˆ{}ˆ{bia E 估计量的方差 })}ˆ{ˆ({}ˆvar{2θθθE E -= 的一致估计为ˆ则称,0}ˆvar{lim ,0}ˆ{bia 若θθθθ==∞→N2.相关法(间接法)进行功率谱估计 相关法的理论基础维纳—辛钦定理 )(][DTFTΩ−−−−→←x x P n R 估计的方法：1) 由随机序列一个样本的N 个观测值计算自相关函数的估计][ˆn R x 2) 对][ˆn Rx 进行DTFT 即得该随机序列的功率谱估计 （2） 自相关函数的估计X[k]是宽平稳各态遍历随机信号，x[k]是其一个样本∑-=∞→++=N Nk N x n k x k x N n R ][][121lim ][ 已知x[k]的N 个观测值x[0],x[1],⋯,x[N-1]，则自相关函数的估计为][][1][ˆ1n k x k x Nn RN kx +=∑-=][*][1n x n x N-=1)1(-≤≤--N n N][ˆn Rx 的计算过程：10-≤≤N n][][1][ˆ10n k x k x Nn RnN kx +=∑--=)1(≤≤--n N∑--=+=1][][1][ˆN nk x n k x k x Nn R∑+-=-=n N ln l x l x N10][][11][][1][10-≤+=∑--=N n n k x k x Nn R nN kx（3） 相关法进行功率谱估计∑-=∧+=10][][1][N kx n k x k x Nn RΩ--=∑=Ωn LLn x x n R P j e ][ˆ)(ˆ}e ][ˆRe{2]0[ˆj 11Ω--=∑+=n N n n R R(4） 相关法功率谱估计的质量功率谱估计的质量与自相关函数估计的质量密切相关][]}[{bia n R Nn n R x x -=∧])[][][(1]}[ˆvar{2n r R n r R r R Nn R r-++≈∑∞-∞=][ˆ),(ˆDFT DTFT,][ˆ估计][m P P n R k x x x x Ω−−−−−−→−−−−−→−N →∞，偏差、方差趋于零，是一致估计。

5.1 求题图5.1中三个电路的传输函数（不考虑输出负载）。

RRC1C 2C 1C 2C 1R 2R题图5.1解根据电路分析、信号与系统的知识， 第一个图中系统的传输函数 1/1()1/1j C H j R j C j RCωωωω==++ 第二个图中系统地传输函数 ()21112211/1()/11/1/j C j RC H j R j C j R C C j C R j C ωωωωωωω+==++++ 第三个图中系统地传输函数()2222212111221212121122/1/()//1/1/R j C R j C R j R R C H j R j C R j C R R j R R C C R j C R j C ωωωωωωωωω++==++++++5.2若平稳随机信号)(t X 的自相关函数||2)(ττ-+=BeA R X ，其中，A 和B 都是正常数。

又若某系统冲击响应为()()wth t u t te -=。

当)(t X 输入时，求该系统输出的均值。

解： 因为[]()22X EX R A =∞=所以[]E X A A =±=±。

()()()()()20wt A E Y t E h X t d E X t h d A te dt wξξξξξ∞∞∞--∞-∞±⎡⎤=-==±=⎡⎤⎡⎤⎣⎦⎣⎦⎢⎥⎣⎦⎰⎰⎰ 5.35.4 若输入信号00()cos()X t X t ω=++Φ作用于正文图5.2所示RC 电路，其中0X 为[0,1]上均匀分布的随机变量，Φ为[0,2π]上均匀分布的随机变量，并且0X 与Φ彼此独立。

求输出信号Y(t)的功率谱与相关函数。

解：首先我们求系统的频率响应()H j ω。

根据电路分析、信号与系统的知识，/1/11()()()1/1t RCj C H j h t e u t R j C j RCRCωωωω-==↔=++ 然后，计算)(t X 的均值与自相关函数，[]()1/2X m E X t ==[]{}(){}{}0000(,)cos cos X R t t EXt X t τωωτ+=++Φ+++Φ=⎡⎤⎣⎦()01/31/2cos ωτ+可见)(t X 是广义平稳的。

第9章 随机信号分析随机信号和确定信号是两类性质完全不同的信号，对它们的描述、分析和处理方法也不相同。

随机信号是一种不能用确定数学关系式来描述的，无法预测未来某时刻精确值的信号，也无法用实验的方法重复再现。

随机信号分为平稳和非平稳两类。

平稳随机信号又分为各态历经和非各态历经。

本章所讨论的随机信号是平稳的且是各态历经的。

在研究无限长信号时，总是取某段有限长信号作分析。

这一有限长信号称为一个样本（或称子集），而无限长信号x(t)称为随机信号总体（或称集）。

各态历经的平稳随机过程中的一个样本的时间均值和集的平均值相等。

因此一个样本的统计特征代表了随机信号总体，这使得研究大大简化。

工程上的随机信号一般均按各态历经平稳随机过程来处理。

仅在离散时间点上给出定义的随机信号称为离散时间随机信号，即随机信号序列。

随机信号序列可以是连续随机信号的采样结果，也可以是自然界里实际存在的物理现象，即它们本身就是离散的。

平稳随机过程在时间上是无始无终的，即其能量是无限的，本身的Fourier 变换也是不存在的；但功率是有限的。

通常用功率谱密度来描述随机信号的频域特征，这是一个统计平均的频谱特性。

平稳随机过程统计特征的计算要求信号x(n)无限长，而实际上这是不可能的，只能用一个样本，即有限长序列来计算。

因此得到的计算值不是随机信号真正的统计值，而仅仅是一种估计。

本章首先介绍随机信号的数字特征，旨在使大家熟悉描述随机信号的常用特征量。

然后介绍描述信号之间关系的相关函数和协方差。

这些是数字信号时间域内的描述。

在频率域内，本章介绍功率谱及其估计方法，并给出了功率谱在传递函数估计方面的应用。

最后介绍描述频率域信号之间关系的函数---相干函数。

9.1 随机信号的数字特征9.1.1 均值、均方值、方差若连续随机信号x(t)是各态历经的，则随机信号x(t)均值可表示为： []⎰∞→==TT x dt t x Tt x E 0)(1)(limμ （9-1）均值描述了随机信号的静态（直流）分量，它不随时间而变化。

随机信号是一种不能用确定的数学关系式来描述的、无法预测未来时刻精确值的信号，也无法用实验的方法重复再现。

换言之，随机信号是指不能用确定性的时间函数来描述，只能用统计方法研究的信号。

其统计特性：概率分布函数、概率密度函数。

统计平均：均值、方差、相关。

随机信号分为平稳和非平稳两大类。

平稳随机信号又分为各态历经和非各态历经。

1） 各态历经信号——指无限个样本在某时刻所历经的状态，等同于某个样本在无限时间里所经历的状态的信号。

2） 平稳随机信号——其均值和相关不随时间变化。

注：各态历经信号一定是随机信号，反之不然。

工程上的随机信号通常都按各态历经平稳随机信号来处理。

仅在离散时间点上给出定义的随机信号称为离散时间随机信号，即随机信号序列。

平稳随机信号在时间上的无限的，故其能量是无限的，只能用功率谱密度来描述随机信号的频域特性。

1. 随机信号的数字特征 均值、均方值、方差若连续随机信号x(t)是各态历经的，则随机信号x(t)的均值可表示为：⎰→∞==TT x dt t x Tt x E 0)(1lim)]([μ均值描述了随机信号的静态分量（直流）。

随机信号x(t)的均方值表达式为：dt t x TTT x)(1lim22⎰→∞=ψ2xψ表示信号的强度或功率。

随机信号x(t)的均方根值表示为：⎰→∞=T T x dt t x T 02)(1limψ x ψ也是信号能量的一种描述。

随机信号x(t)的方差表达式为：⎰-==-→∞Tx T x x dx t x Tx E 0222])([1lim])[(μσμ2xσ是信号的幅值相对于均值分散程度的一种表示，也是信号纯波动分量（交流）大小的反映。

随机信号x(t)的均方差（标准差）可表示为⎰-=→∞T x T x dx t x T 02])([1limμσ 它和2x σ意义相同。

平稳随机过程统计特征的计算要求信号x(t)无限长，而实际上只能用一个样本即有限长序列来计算。

读书报告——随机信号分析基础本读书报告主要分为三部分： 一、 自学计划。

二、理论原理知识。

三、个人总结及心得体会。

一、 自学计划。

在研究生第一学期，开设了随机信号分析基础课，这门课程是在信号分析基础上对信号分析与处理的更深一步的学习。

11月末，在老师的安排下我们开始进行关于由王永德、王军主编的，由电子工业出版社出版的《随机信号分析基础》（第二版），第5章随机信号通过线性系统的自学。

（1） 时间安排11月末至12月末，每周的周一下午，周四上午设定为学习时间。

（2） 目标要求理解第五章关于5.2，5.3，5.5的相关内容，随时做好学习相关知识的笔记及心得体会。

二、 理论原理知识。

在学习本书之前我已经完成了《高等数学》、《复变函数》、《信号与系统》等基础课程的学习。

并且在学习第5章之前，学习了前四章的相关知识。

第2、3、4章讨论了随机过程的一般概念及其统计特征。

各种电子系统尽管种类繁多，作用各异，但基本上可分为两大类：即线性统计与非线性统计。

第五章研究的是现性系统问题并在5.5节开始随机序列通过线性离散系统后统计特性的变化，并介绍随机序列模型的概念与现代谱值的基本思想。

以下为关于5.2，5.3及5.5的读书笔记。

5.2 随机信号通过线性系统 主要研究输入信号为随机过程时，线性、稳定性、是不变系统的统计特征。

5.2.1线性系统输出的统计特征 1.系统的输出系统的输入输出样本函数之间的关系：()()()Y t h X t d τττ+∞-∞=-⎰，输入随机过程为()X t ，通过系统产生的新过程为()Y t ，对于有收敛的样本函数都可以通过此关系求得输出。

2.系统输出的均值与自相关函数 主要为解决已知输入随机过程的均值和自相关函数，求系统的输出随机过程的均值和自相关函数。

（1） 系统输出均值若()X t 是有界平稳过程，于是[()][()()] ()X E Y t E h X t d m h d τττττ+∞-∞+∞-∞=-=⎰⎰显然X m 是与时间无关的常数。