【德阳二模】·2014届四川省德阳市高三二诊考试文科数学试题(含答案解析)扫描版
- 格式:pdf
- 大小:384.02 KB
- 文档页数:9

四川省德阳市2022-2021学年高一下学期期末数学试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U={1,2,3,4,5},A={1,2},B={2,3,4},则(∁U A)∩B=()A.{2,3} B.{3,4} C.{3} D.{4}2.已知各项均不为0的数列{a n}满足:a n+1﹣3a n=0,则=()A.B.3C.D.273.过点(1,﹣1)的直线l与直线:﹣5x+y=0平行,则l在纵轴上的截距是()A.﹣4 B.4C.﹣6 D.64.设m<0,﹣1<n<0,则m,mn,mn2三者的关系大小为()A.m<mn2<mn B.m<mn<mn2C.m n2<m<mn D.mn2<mn<m5.指数函数y=a x(a>0,a≠1)在区间[﹣1,1]上的最大值与最小值之差等于,则常数a的值是()A.2B.C.2或D.2或6.要得到函数的图象,只要将函数y=sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位7.已知平面直角坐标系xOy上的区域D 由不等式组确定,若M(x,y)为D上的动点,则Z=x+y的最大值为()A.4B.4C.3D.38.在△ABC中,sin2C=(sinA﹣sinB)2+sinAsinB,则C的值是()A.B.C.D .9.三角形ABC满足,||=||,点M为边BC的中点,且||=4,=0,则边AC的长度为()A.4B.4C.8D.810.已知二次函数f(x)=x2﹣2x+ab(a≠b)有唯一的零点,则代数式||的最小值是()A.8B.6C.4D.4二、填空题(本大题共5小题,每小题5分,共25分,把正确答案填在答题卡的横线上)11.原点到直线3x﹣4y﹣5=0的距离为.12.设tanα,tanβ是方程x2﹣3x+2=0的两个根,则tan(α+β)的值为.13.已知等差数列{a n}的前n项和S n=n2+n,则a3=.14.已知直线l1∥l2,A是l1,l2之间的肯定点,并且A点到l1,l2的距离分别为h1,h2,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC面积的最小值为.15.有以下5个命题:①若P(a,b),Q(c,d)是直线y=kx+m上两个不同的点,则|PQ|可以表示为|c﹣a|;②若||=1.||=,且()⊥,则与的夹角为45°;③三角形的三边分别是4,5,6,则该三角形的最大内角是最小内角的两倍;④在平面直角坐标系中全部直线都有倾斜角,但不是全部直线都有斜率,且倾斜角越大,则斜率越大;⑤若三角形ABC的重心为P ,则.其中正确的命题是.(写出全部正确命题的序号)三、解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤)16.已知O(0,0),M(﹣1,﹣2),N(3,n)均在直线l上,(1)求n的值及直线l的斜率;(2)若点P为直线l上一个动点,A(1,5),B(7,1),求的最小值.17.已知向量=(1,1),=(x,3),,;(1)若,求x 的值,并推断与同向还是反向;(2)若向量在向量方向上的投影为,求x的值.18.已知函数f(x)=sinωx+cosωx(ω>0)的最小正周期为π,(1)求ω的值与函数f(x)的图象的对称轴方程;(2)若角A为△ABC的最小内角,求f(A)的取值范围.19.已知△ABC的内角A,B,C所对的边分别为a,b,c,且满足bcosA+acosB=2ccosC,c=;(1)若A=,求边b的长;(2)求△ABC面积的最大值.20.已知数列{a n}是公比为d的等比数列,且a1与a2的算术平均数恰好是a3;(1)求d;(2)设{b n}是以2为首项,d为公差的递减等差数列,其前n项和为S n,比较S n与b n的大小.21.已知实数a>0,定义域为(﹣1,1)的函数f(x)=+a;(1)当a=1时,用定义判定f(x)的奇偶性并求(x)的最小值.(2)用定义证明函数g(x)=x+(k>0)在(0,)上单调递减,则(,+∞)上单调递增;(3)利用(2)的结论求实数a的取值范围,使得对于区间[0,]上的任意三个实数r,s,t,都存在以f(r),f(s),f(t)为边长的三角形.四川省德阳市2022-2021学年高一下学期期末数学试卷(文科)一、选择题(本大题共10小题,每小题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集U={1,2,3,4,5},A={1,2},B={2,3,4},则(∁U A)∩B=()A.{2,3} B.{3,4} C.{3} D.{4}考点:交、并、补集的混合运算.专题:集合.分析:依据集合的基本运算进行求解即可.解答:解:∵U={1,2,3,4,5},A={1,2},B={2,3,4},∴(∁U A)∩B={3,4,5}∩{2,3,4}={3,4},故选:B点评:本题主要考查集合的基本运算,比较基础.2.已知各项均不为0的数列{a n}满足:a n+1﹣3a n=0,则=()A.B.3C.D.27考点:等比数列的通项公式.专题:等差数列与等比数列.分析:依据条件a n+1﹣3a n=0,得到数列{a n}为等比数列,依据等比数列的通项公式进行求解即可.解答:解:a n+1﹣3a n=0,∴a n+1=3a n,则数列{a n}为等比数列,公比q=3,则=q3=33=27,故选:D.点评:本题主要考查等比数列的性质和通项公式的应用,推断数列是等比数列是解决本题的关键.3.过点(1,﹣1)的直线l与直线:﹣5x+y=0平行,则l在纵轴上的截距是()A.﹣4 B.4C.﹣6 D.6考点:直线的一般式方程与直线的平行关系.专题:直线与圆.分析:由平行关系可得直线的斜率,可得直线的方程,令x=0解得y值即为截距.解答:解:由题意可得直线﹣5x+y=0的斜率为5,由平行关系可得直线l的斜率也为5,∴所求直线方程为y+1=5(x﹣1),令x=0可得y=﹣6,∴l在纵轴上的截距为﹣6故选:C.点评:本题考查直线的一般式方程和平行关系,属基础题.4.设m<0,﹣1<n<0,则m,mn,mn2三者的关系大小为()A.m<mn2<mn B.m<mn<mn2C.m n2<m<mn D.mn2<mn<m考点:不等式的基本性质.专题:不等式的解法及应用.分析:利用不等式的基本性质即可得出.解答:解:∵m<0,﹣1<n<0,∴n<n2<1,∴m<mn2<mn.故选:A.点评:本题考查了不等式的基本性质,属于基础题.5.指数函数y=a x(a>0,a≠1)在区间[﹣1,1]上的最大值与最小值之差等于,则常数a的值是()A.2B.C.2或D.2或考点:指数函数的图像与性质.专题:函数的性质及应用.分析:对底数a分类争辩,分别依据指数函数的单调性求出函数的最大、小值,由条件列出方程求出a的值.解答:解:①当a>1时,y=a x在区间[﹣1,1]上的最大值是a ,最小值是,∴a ﹣=,则2a2﹣3a﹣2=0,解得a=2或(舍去),则a=2;②当a>1时,y=a x在区间[﹣1,1]上的最小值是a ,最大值是,∴﹣a=,则2a2+3a﹣2=0,解得a=或﹣2(舍去),则a=,综上可得,a 的值是或2,故选:C.点评:本题考查指数函数的单调性,以及分类争辩思想,属于基础题.6.要得到函数的图象,只要将函数y=sin2x的图象()A.向左平移个单位B.向右平移个单位C.向左平移个单位D.向右平移个单位考点:函数y=Asin(ωx+φ)的图象变换.专题:计算题.分析:依据平移的性质,,依据平移法则“左加右减”可知向右平移个单位.解答:解:∵故选:D点评:本题主要考查三角函数的平移.三角函数的平移原则为左加右减上加下减.但要留意平移量是而不是,平移量是指x的变化量.7.已知平面直角坐标系xOy上的区域D 由不等式组确定,若M(x,y)为D上的动点,则Z=x+y的最大值为()A.4B.4C.3D.3考点:简洁线性规划.专题:不等式的解法及应用.分析:画出满足已知不等式组确定的可行域,并求出各角点的坐标,代入目标函数中分别求出目标函数的值,比较后可得目标函数的最大值解答:解:满足不等式组确定的可行域如下图中阴影部分所示:∵z=x+y,则y=﹣x+z,∴z O=0,z A=3,z B=4,z C=2,故z=的最大值为4;故选A.点评:本题考查的学问点是简洁的线性规划,娴熟把握角点法是快速精确的解答线性规划题的关键;考查了数形结合的思想.8.在△ABC中,sin2C=(sinA﹣sinB)2+sinAsinB,则C的值是()A.B.C.D .考点:余弦定理;正弦定理.专题:解三角形.分析:原式可化简为a2+b2﹣c2=ab,由余弦定理知cosC==,即可求得C的值.解答:解:∵已知等式sin2C=(sinA﹣sinB)2+sinAsinB=sin2A+sin2B﹣sinAsinB,∴sin2C+sinAsinB=sin2A+sin2B,利用正弦定理化简得:c2+ab=a2+b2,即a2+b2﹣c2=ab,∴cosC==,又0<C<π,∴C=;故选:C.点评:本题主要考察了正弦定理、余弦定理的综合应用,属于中档题.9.三角形ABC满足,||=||,点M为边BC的中点,且||=4,=0,则边AC的长度为()A.4B.4C.8D.8考点:平面对量数量积的运算.专题:平面对量及应用.分析:依据平面对量的加减法的几何意义分析以AB,AC为邻边的平行四边形的外形,求AC.解答:解:由三角形ABC满足,||=||,依据平行四边形法则,可知以AB,AC为邻边的平行四边形对角线相等,所以是矩形,又点M为边BC的中点,且||=4,=0,所以得到对角线垂直,所以AC=AM=4;故选:A.点评:本题考查了平面对量的加法和减法的几何意义以及数量积为0的几何意义的运用.10.已知二次函数f(x)=x2﹣2x+ab(a≠b)有唯一的零点,则代数式||的最小值是()A.8B.6C.4D.4考点:二次函数的性质.专题:函数的性质及应用.分析:由二次函数f(x)有唯一零点,便有△=0,这样便得到ab=1,从而2ab=2,从而有,依据基本不等式即可求出原代数式的最小值.解答:解:二次函数f(x)有唯一零点;∴△=4﹣4ab=0;∴ab=1;∴=;∴原代数式的最小值是4.故选:D.点评:考查函数零点的概念,二次函数有一个零点时的判别式△的取值状况,分别常数法的运用,基本不等式用于求最小值.二、填空题(本大题共5小题,每小题5分,共25分,把正确答案填在答题卡的横线上)11.原点到直线3x﹣4y﹣5=0的距离为1.考点:点到直线的距离公式.专题:直线与圆.分析:利用点到直线的距离公式解答.解答:解:原点到直线3x﹣4y﹣5=0的距离为:=1;故答案为:1.点评:本题考查了点到直线的距离公式的运用;熟记公式是关键.12.设tanα,tanβ是方程x2﹣3x+2=0的两个根,则tan(α+β)的值为﹣3.考点:两角和与差的正切函数.专题:计算题.分析:由tanα,tanβ是方程x2﹣3x+2=0的两个根,利用根与系数的关系分别求出tanα+tanβ及tanαtanβ的值,然后将tan(α+β)利用两角和与差的正切函数公式化简后,将tanα+tanβ及tanαtanβ的值代入即可求出值.解答:解:∵tanα,tanβ是方程x2﹣3x+2=0的两个根,∴tanα+tanβ=3,tanαtanβ=2,则tan(α+β)==故答案为:﹣3点评:此题考查了两角和与差的正切函数公式,以及根与系数的关系,利用了整体代入的思想,娴熟把握公式是解本题的关键.13.已知等差数列{a n}的前n项和S n=n2+n,则a3=6.考点:等差数列的通项公式.专题:综合题;分类争辩.分析:依据等差数列的前n项和公式,分两种状况考虑:当n=1时,得到a1=S1;当n大于等于2时,利用a n=S n﹣S n﹣1即可得点a n的通项公式,把n=1代入也满足,进而得到数列的通项公式,然后令n=3代入通项公式即可求出a3的值.解答:解:当n=1时,得到a1=S1=2,当n≥2时,a n=S n﹣S n﹣1=(n2+n)﹣[(n﹣1)2+(n﹣1)]=2n,把n=1代入a n得:a1=2满足,所以等差数列{a n}的通项公式a n=2n,则a3=2×3=6.故答案为:6点评:此题考查同学机敏运用数列的递推式求出通项公式,机敏运用等差数列的通项公式化简求值,是一道中档题.求等差数列通项公式时留意把n=1代入检验.14.已知直线l1∥l2,A是l1,l2之间的肯定点,并且A点到l1,l2的距离分别为h1,h2,B是直线l2上一动点,作AC⊥AB,且使AC与直线l1交于点C,则△ABC 面积的最小值为h 1•h2.考点:点到直线的距离公式.专题:直线与圆.分析:过A 作l1、l 2的垂线,分别交l1、l2于E、F .设∠FAC=θ,由直角三角形中三角函数的定义,算出AC=且AB=,从而得到△ABC面积S=AB•AC=,利用正弦函数的有界性,可得θ=时△ABC面积有最小值h1•h2.解答:解:过A作l1、l2的垂线,分别交l 1、l2于E、F,则AF=h1,AE=h2,设∠FAC=θ,则Rt△ACF中,AC=,Rt△ABE中,∠ABE=θ,可得AB=,∴△ABC面积为S=AB•AC=,∵θ∈(0,)∴当且仅当θ=时,sin2θ=1达到最大值1,此时△ABC面积有最小值h1•h2,故答案为:h1•h2点评:此题考查了直角三角形中锐角三角函数定义,正弦函数的定义域及值域及二倍角的正弦函数公式,利用了数形结合的思想,属于中档题.15.有以下5个命题:①若P(a,b),Q(c,d)是直线y=kx+m上两个不同的点,则|PQ|可以表示为|c﹣a|;②若||=1.||=,且()⊥,则与的夹角为45°;③三角形的三边分别是4,5,6,则该三角形的最大内角是最小内角的两倍;④在平面直角坐标系中全部直线都有倾斜角,但不是全部直线都有斜率,且倾斜角越大,则斜率越大;⑤若三角形ABC的重心为P,则.其中正确的命题是①③⑤.(写出全部正确命题的序号)考点:命题的真假推断与应用.专题:简易规律.分析:由条件利用两点间的距离公式、两个向量的夹角公式、余弦定理、直线的倾斜角和斜率、三角形的重心的性质,逐一推断各个选项是否正确,从而得出结论.解答:解:∵P(a,b),Q(c,d)是直线y=kx+m上两个不同的点,则b=ka+m,d=kc+m,∴|PQ|===|c﹣a|,故①正确.②若||=1,||=,且()⊥,则()⊥=+•=1+1×2×cos<,>=0,求得cos<,>=﹣,可得与的夹角<,>=120°,故②不正确.③三角形的三边分别是4,5,6,则该三角形的最大内角为α,最小内角为β,则由余弦定理可得cosα==,cosβ==,2cos2β﹣1==cosα,∴α=2β,即该三角形的最大内角是最小内角的两倍,故③正确.在平面直角坐标系中全部直线都有倾斜角,但不是全部直线都有斜率,但不是倾斜角越大,则斜率越大,如倾斜角为60°的直线斜率为,而倾斜角为120°的直线的斜率为﹣,故④不正确.⑤若三角形ABC的重心为P,线段BC的中点为D,则由三角形的重心的性质可得PA=2PD,而=2,则有+=﹣,即,故⑤正确,故答案为:①③⑤.点评:本题主要考查命题的真假的推断,两点间的距离公式、两个向量的夹角公式、余弦定理、直线的倾斜角和斜率、三角形的重心的性质,属于中档题.三、解答题(本大题共6小题,共75分,解答应写出文字说明、证明过程或演算步骤)16.已知O(0,0),M(﹣1,﹣2),N(3,n)均在直线l上,(1)求n的值及直线l的斜率;(2)若点P为直线l上一个动点,A(1,5),B(7,1),求的最小值.考点:平面对量数量积的运算;直线的斜率.专题:平面对量及应用;直线与圆.分析:(1)利用O,M两点求直线方程,再由N在直线l上求n;(2)由(1)设P(x,2x),利用坐标表示,依据表达式求最小值.解答:解:(1)由题意直线l 的方程为y=2x,所以n=6,直线l的斜率为2.(2)由(1)设p(x,2x),则=(1﹣x,5﹣2x)•(7﹣x,1﹣2x)=5x2﹣20x+12=5(x﹣2)2﹣8,所以当x=2时,即P(2,4)时,的最小值为﹣8.点评:本题考查了直线方程的求法以及平面对量的数量积、二次函数求最值;属于基础题.17.已知向量=(1,1),=(x,3),,;(1)若,求x 的值,并推断与同向还是反向;(2)若向量在向量方向上的投影为,求x的值.考点:平面对量数量积的运算;平面对量共线(平行)的坐标表示.专题:平面对量及应用.分析:(1)先写出向量的坐标,依据平行向量的坐标关系即可建立关于x的方程,解出x,从而便得到的坐标,依据坐标即可推断的方向;(2)依据投影的计算公式有,进行数量积的坐标运算即可解出x.解答:解:(1)=(1+2x,7),;∵∥;∴﹣(1+2x)﹣7(2﹣x)=0;∴x=3,此时;∴;∴与反向;(2)向量在方向上的投影为;∴解得x=﹣1.点评:考查向量坐标的加法、减法,及数乘运算,平行向量的坐标关系,数乘的几何意义,以及向量投影的计算公式,向量数量积的坐标运算.18.已知函数f(x)=sinωx+cosωx(ω>0)的最小正周期为π,(1)求ω的值与函数f(x)的图象的对称轴方程;(2)若角A为△ABC的最小内角,求f(A)的取值范围.考点:三角函数中的恒等变换应用;正弦函数的图象.专题:三角函数的求值;三角函数的图像与性质.分析:(1)由三角函数中的恒等变换应用化简可得f(x)=2sin(ωx+),利用周期公式可求ω,令2x+=k,则x=,即求得函数f(x)的图象的对称轴方程.(2)由题意可得0<A,可得2A,求得2sin(2A+)∈[0,2],即可得解.解答:解:(1)由题意可得f(x)=2sin(ωx+),∵,可得ω=2.即f(x)=2sin(2x+),令2x+=k,则x=,即函数f(x)的图象的对称轴方程为:x=(k∈Z)…6分(2)由题意可得0<A,∴2A,∴sin(2A+)∈[0,1],∴2sin(2A+)∈[0,2],即f(A)的取值范围为[0,2]…12分点评:本题主要考查了三角函数中的恒等变换应用,正弦函数的图象和性质,属于基本学问的考查.19.已知△ABC的内角A,B,C所对的边分别为a,b,c,且满足bcosA+acosB=2ccosC,c=;(1)若A=,求边b的长;(2)求△ABC面积的最大值.考点:余弦定理;正弦定理.专题:解三角形.分析:(1)由正弦定理化简已知等式可得sinC=2sinCcosC,结合范围C∈(0,π),可求C,B的值,利用正弦定理即可求得B的值.(2)利用余弦定理及基本不等式的应用可得3=a2+b2﹣ab≥2ab﹣ab=ab(当且仅当a=b时取等号),利用三角形面积公式即可得解.解答:解:(1)由题意可得sinBcosA+sinAcosB=2sinCcosC,∴sin(A+B)=2sinCcosC,即sinC=2sinCcosC,又sinC≠0,∴cosC=,又C∈(0,π),∴C=,∴B=,又c=,在△ABC中,∵,∴b=…6分(2)在△ABC中,∵c2=a2+b2﹣2abcosC,且c=,C=,∴3=a2+b2﹣ab≥2ab﹣ab=ab(当且仅当a=b时取等号),∴S△ABC =(当且仅当a=b时取等号),即当△ABC为正三角形时,△ABC 面积的最大值为…12分点评:本题主要考查了正弦定理,余弦定理,三角形面积公式,基本不等式的综合应用,属于基本学问的考查.20.已知数列{a n}是公比为d的等比数列,且a1与a2的算术平均数恰好是a3;(1)求d;(2)设{b n}是以2为首项,d为公差的递减等差数列,其前n项和为S n,比较S n与b n的大小.考点:等比数列的通项公式;等比数列的前n项和.专题:等差数列与等比数列.分析:(1)依据条件建立方程关系即可求d;(2)求出S n与b n的表达式,利用作差法进行比较即可.解答:解:(1)∵a1与a2的算术平均数恰好是a3;∴a1+a1d=2a1d2,∵a1≠0,∴2d2﹣d﹣1=0,解得d=1或d=﹣.(2)∵{b n}是以2为首项,d为公差的递减等差数列,∴d=﹣,则b n=2+(n﹣1)()=+.前n项和为S n =2n+=,S n﹣b n =﹣(+)==,故当n=1或n=10时,S n=b n,当1<n<10时,S n>b n,当n>10,且n∈N时,S n<b n.点评:本题主要考查等比数列和等差数列的通项公式和前n项和公式的应用,考查同学的运算力量.21.已知实数a>0,定义域为(﹣1,1)的函数f(x)=+a;(1)当a=1时,用定义判定f(x)的奇偶性并求(x)的最小值.(2)用定义证明函数g(x)=x+(k>0)在(0,)上单调递减,则(,+∞)上单调递增;(3)利用(2)的结论求实数a的取值范围,使得对于区间[0,]上的任意三个实数r,s,t,都存在以f(r),f(s),f(t)为边长的三角形.考点:奇偶性与单调性的综合;函数奇偶性的性质.专题:函数的性质及应用.分析:(1)依据函数奇偶性的定义进行推断函数的奇偶性,化简函数,即可求f(x)的最小值;(2)利用函数单调性的定义,利用定义法进行证明;(3)利用换元法将结合(2)的结论将问题转化为在区间上,恒有2y min>y max.解答:解:(1)当a=1时,f(x)=+,定义域为(﹣1,1),则f(﹣x)=+=f(x),则函数f(x)为偶函数,f(x)=+==,∵x∈(﹣1,1),∴1﹣x2∈(0,1],∴∈(0,1],∴当=1时,f(x)取得最小值为2;(2)设0<x1<x2<,则f(x1)﹣f(x2)=x1+﹣(x2+)=(x1﹣x2)•.由0<x1<x2<,可得(x1﹣x2)<0,0<x1x2<k,∴(x1﹣x2)•>0,f(x1)>f(x2),故函数在(0,)上单调递减.设<x1<x2,同理可得f(x1)﹣f(x2)=(x1﹣x2)•<0,即f(x1)<f(x2),故函数在(,+∞))上单调递增.(3)设t=,则当x∈[0,]时,可得,∴从而原问题等价于求实数a的范围,使得在区间上,恒有2y min>y max.①当时,在上单调递增,∴,由2y min>y max得,从而;②当时,在上单调递减,在上单调递增,∴,由2y min>y max得,从而;③当时,在上单调递减,在上单调递增,∴y min=2,y max=a+1,由2y min>y max得,从而;④当a≥1时,在上单调递减,∴,由2y min>y max得,从而;综上,.点评:本题考查函数的奇偶性和单调性的推断,以及函数y=x+(k>0)的单调性的证明和应用,利用定义法是解决本题的关键.考查同学分析转化问题的力量,运算量较大,属于难题.。

德阳市高中2015级“二诊”考试数学试卷(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知为虚数单位,实数,满足,则()A. 1B.C.D.【答案】D【解析】,则故选D.2. 已知集合,集合,若,则()A. B. C. D.【答案】A【解析】得到,故选A.3. 函数的图象向右平移个单位后所得的图象关于原点对称,则可以是()A. B. C. D.【答案】B【解析】由题函数的图象向右平移个单位后所得的图象关于原点对称,即平移后得到的函数为奇函数,即为奇函数,对照选项可知选B.4. 实验测得四组数对的值为,,,,则与之间的回归直线方程是()参考公式:,.A. B.C. D.【答案】A【解析】样本中心点为,计算得,代入验证可知选项正确.5. 如图所示的三视图表示的几何体的体积为,则该几何体的外接球的表面积为()A. B. C. D.【答案】C【解析】由三视图可得该几何体为底面边长为,一条侧棱垂直底面的四棱锥,设高为4,则,将该几何体补成一个长方体,则其外接球半径为故这个几何体的外接球的表面积为.故选C.【点睛】本题考查了由三视图,求体积和表面积,其中根据已知的三视图,判断几何体的形状是解答的关键.属于中档题.6. 《九章算术》是我国古代一部数学名著,某数学爱好者阅读完其相关章节后编制了如图的程序框图,其中表示除以的余数,例如.若输入的值为8时,则输出的值为()A. 2B. 3C. 4D. 5【答案】B【解析】模拟执行程序框图,可得:满足条件,满足条件满足条件,不满足条件,,满足条件,满足条件,…,可得:2, 4, 8,∴共要循环3次,故.故选B.7. 已知,则、、的大小排序为()A. B.C. D.【答案】A【解析】为正实数,且,可得:即因为函数单调递增,∴.故选A.8. 以等腰直角三角形的斜边上的中线为折痕,将与折成互相垂直的两个平面,得到以下四个结论:①平面;②为等边三角形;③平面平面;④点在平面内的射影为的外接圆圆心.其中正确的有()A. ①②③B. ②③④C. ①②④D. ①③④【答案】C【解析】由于三角形为等腰直角三角形,故,所以平面,故①正确,排除选项.由于,且平面平面,故平面,所以,由此可知,三角形为等比三角形,故②正确,排除选项.由于,且为等边三角形,故点在平面内的射影为的外接圆圆心, ④正确,故选.9. 已知双曲线的离心率为,其一条渐近线被圆截得的线段长为,则实数的值为()A. 3B. 1C.D. 2【答案】D【解析】双曲线的离心率为,则故其一条渐近线不妨为,圆的圆心,半径为2,双曲线的一条渐近线被圆截得的线段长为,可得圆心到直线的距离为:故选D.10. 已知函数,若,使得成立,则实数的取值范围是()A. B. C. D.【答案】A【解析】由于,函数为增函数,且,函数为奇函数,故,即在上存在.画出的图象如下图所示,由图可知,,故选.【点睛】本小题主要考查函数的单调性与奇偶性,考查利用导数研究函数的单调性,考查恒成立问题的解题思路.给定一个函数的解析式,首先要分析这个函数的定义域,单调性与奇偶性等等性质,这些对于解有关函数题目可以有个方向,根据基本初等函数的单调性要熟记.11. 如图,过抛物线的焦点作倾斜角为的直线,与抛物线及其准线从上到下依次交于、、点,令,,则当时,的值为()A. 3B. 4C. 5D. 6【答案】C【解析】设,则又,可得同理可得,故选B.12. 已知、是函数(其中常数)图象上的两个动点,点,若的最小值为0,则函数的最大值为()A. B. C. D.【答案】B【解析】由题,当点、分别位于分段函数的两支上,且直线分别与函数图像相切时,最小,设当时,直线因为点在直线直线上,解得同理可得则,且函数在上单调递增,在上单调递见,故函数的最大值为. 故选B.第Ⅱ卷(非选择题共90分)二、填空题:共4小题,每小题5分,共20分.将答案填在答题卡上.13. 已知实数,满足条件,则的最大值为__________.【答案】8【解析】画出可行域如图所示,则当目标函数y经过点时取代最大值,即答案为4.14. 为弘扬我国优秀的传统文化,某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则的值为__________.【答案】【解析】,解得,根据中位数为,可知,故.15. 如图,在三角形中,、分别是边、的中点,点在直线上,且,则代数式的最小值为__________.【答案】【解析】不妨设为直角,且,以分别为轴,此时为点的坐标,表示到原点的距离,最短时为点到直线的距离,由于是中位线,故最短的等于点到距离的一半,即.16. 已知中,角、、所对的边分别是、、且,,,若为的内心,则的面积为__________.【答案】【解析】由于,所以,展开化简得.由正弦定理得,所以,解得.设,设外切圆半径为,根据海伦公式有,解得,故.【点睛】本小题主要考查正弦定理和余弦定理解三角形,考查了三角形的面积公式,包括海伦公式及有关内切圆的面积公式.首先根据,及,得到,利用两角和与差的正弦公式和二倍角公式,化简这个式子可求得的值.利用海伦公式可求得面积.三、解答题:解答应写出文字说明、证明过程或演算步骤.17. 已知数列满足,.(1)求证:数列为等比数列;(2)求数列的前项和.【答案】(1)见解析;(2).【解析】【试题分析】(1)利用配凑法将已知配凑成等比数列的形式,由此证得为等比数列.(2)由(1)求得的通项公式,利用裂项求和法求得数列的前项和.【试题解析】(1)∵,∴.又,∴,.∴是以2为首项,2为公比的等比数列.(2)由(1)知,∴,∴.18. 省环保厅对、、三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:城城城已知在这180个数据中随机抽取一个,恰好抽到记录城市空气质量为优的数据的概率为0.2.(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在城中应抽取的数据的个数;(2)已知,,求在城中空气质量为优的天数大于空气质量为良的天数的概率.【答案】(1)9;(2).【解析】【试题分析】(1)由计算出,再由总数计算出,按比例计算得应抽人数.(2)由(1)知,且,,利用列举法和古典概型计算公式计算得相应的概率.【试题解析】(1)由题意得,即.∴,∴在城中应抽取的数据个数为.(2)由(1)知,且,,∴满足条件的数对可能的结果有,,,,,,,共8种.其中“空气质量为优的天数大于空气质量为良的天数”对应的结果有,,共3种.∴在城中空气质量为优的天数大于空气质量为良的天数的概率为.19. 如图,在四棱锥中,底面为菱形,,平面,,点、分别为和的中点.(1)求证:直线平面;(2)求点到平面的距离.【答案】(1)见解析;(2).【解析】【试题分析】(1)取的中点,连结、,通过证明四边形为平行四边形,得到,由此证得平面.(2)利用等体积法,通过建立方程,由此求得点到面的距离.【试题解析】(1)取的中点,连结、,由题意,且,且,故且,所以,四边形为平行四边形,所以,,又平面,平面,所以,平面.(2)设点到平面的距离为.由题意知在中,,在中,在中,故,,,,所以由得:,解得.20. 已知椭圆:的两个焦点与短轴的一个端点构成的三角形的面积为,且椭圆的离心率为.(1)求椭圆的方程;(2)过点且斜率不为零的直线与椭圆交于两点、,点,试探究:直线与的斜率之积是否为常数.【答案】(1);(2)见解析.【解析】【试题分析】(1)根据三角形面积公式和离心率建立方程,解方程组可求得的值.(2)设出直线的方程联立直线的方程和椭圆的方程,写出韦达定理,通过计算.化简后可得为常数. 【试题解析】(1)由题意得(其中椭圆的半焦距),解得.所以椭圆的方程为:.(2)由题意设直线的方程为:,,,由得:,所以,故,,(常数).21. 已知函数.(1)若是的一个极值点,求的最大值;(2)若,,都有,求实数的取值范围.【答案】(1);(2).【解析】【试题分析】(1)求出函数的导数,通过求得的值,根据单调区间求得函数的最大值.(2)将原不等式转化为,构造函数,对求导,对两者比较大小,分成两类,利用分离常数法求得的取值范围.【试题解析】(1),由题意得,即,所以,所以,当时,;当时,,所以在上单调递增,在上单调递减.所以.(2)由题意得,都有,令函数,当时,在上单调递增,所以在上恒成立,即在上恒成立,令,,则,所以在上单调递减,故,所以实数的取值范围为.同理,当时,在上单调递减,所以在上恒成立,即在上恒成立,令,,则,所以在上单调递减,故.所以实数的取值范围为,综上,实数的取值范围为.【点睛】本小题主要考查函数导数与极值,考查函数导数与不等式恒成立问题. 与函数最值有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.请考生在22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一题记分,做答时,请用2B铅笔在答题卡上将所选题号后的方框涂黑.22. 在平面直角坐标系中,直线:(为参数),以坐标原点为极点,轴正半轴为极轴,建立极坐标系,曲线:.(1)求直线的极坐标方程及曲线的直角坐标方程;(2)记射线与直线和曲线的交点分别为点和点(异于点),求的最大值. 【答案】(1)直线的极坐标方程为:,曲线的直角坐标方程为:;(2). 【解析】试题分析:(1)根据极坐标方程、参数方程与普通方程的对应关系即可得出答案;(2)由(1),,所以,即可得到的最大值.试题解析:(1)由题意得直线的普通方程为:,所以其极坐标方程为:.由得:,所以,所以曲线的直角坐标方程为:.(2)由题意,,所以,由于,所以当时,取得最大值:.23. 已知函数.(1)解关于的不等式;(2)若关于的不等式的解集非空,求实数的取值范围. 【答案】(1);(2).【解析】试题分析:(1)由题意或,由此可解不等式;(2)由于关于的不等式的解集非空,函数的最小值为-1,由此解得的范围.试题解析:(1)由题意或,所以或,即或,或或,故原不等式的解集为.(2),由于,所以当时,的最小值为-1.所以实数的取值范围为:.【点睛】本题主要考查绝对值的意义,绝对值不等式的解法,体现了等价转化的数学思想,属于中档题。
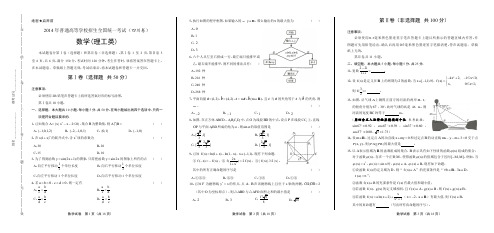
数学试卷 第1页(共18页) 数学试卷 第2页(共18页) 数学试卷 第3页(共18页)绝密★启用前2014年普通高等学校招生全国统一考试(四川卷)数学(理工类)本试题卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题).第Ⅰ卷1至2页,第Ⅱ卷3至6页,共6页.满分150分.考试时间120分钟.考生作答时,须将答案答在答题卡上,在本试题卷、草稿纸上答题无效.考试结束后,将本试题卷和答题卡一并交回.第Ⅰ卷(选择题 共50分)注意事项:必须使用2B 铅笔在答题卡上将所选答案对应的标号涂黑. 第Ⅰ卷共10小题.一、选择题:本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知集合2{|20}A x x x =--≤,集合B 为整数集,则A B = ( )A .{1,0,1,2}-B .{2,1,0,1}--C .{0,1}D .{1,0}- 2.在6(1)x x +的展开式中,含3x 项的系数为( )A .30B .20C .15D .103.为了得到函数sin(21)y x =+的图象,只需把函数sin 2y x =的图象上所有的点( )A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度 4.若0a b >>,0c d <<,则一定有( )A .a bc d > B .a b c d < C .a b d c> D .a b d c<5.执行如图的程序框图,如果输入的x ,y ∈R ,那么输出的S 的最大值为( )A .0B .1C .2D .36.六个人从左至右排成一行,最左端只能排甲或乙,最右端不能排甲,则不同的排法共有( ) A .192 种B .216 种C .240 种D .288 种7.平面向量a (1,2)=,b (4,2)=,c m =a +b ()m ∈R ,且c 与a 的夹角等于c 与b 的夹角,则m =( )A .2-B .1-C .1D .28.如图,在正方体1111ABCD A B C D -中,点O 为线段BD 的中点.设点P 在线段1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是 ( )A.B .C .[]33D .[39.已知()ln(1)ln(1)f x x x =+--,(1,1)x ∈-.现有下列命题:①()()f x f x -=-;②22()2()1xf f x x =+;③|()|2||f x x ≥.其中的所有正确命题的序号是( )A .①②③B .②③C .①③D .①②10.已知F 为抛物线2y x =的焦点,点A ,B 在该抛物线上且位于x 轴的两侧,2OA OB =(其中O 为坐标原点),则ABO △与AFO △面积之和的最小值是( )A .2B .3CD 第Ⅱ卷(非选择题 共100分)注意事项:必须使用0.5毫米黑色墨迹签字笔在答题卡上题目所指示的答题区域内作答.作图题可先用铅笔绘出,确认后再用0.5毫米黑色墨迹签字笔描清楚.答在试题卷、草稿纸上无效.第Ⅱ卷共11小题.二、填空题:本大题共5小题,每小题5分,共25分. 11.复数22i1i-=+ . 12.设()f x 是定义在R 上的周期为2的函数,当[1,1)x ∈-时,242,10,(),01,x x f x x x ⎧-+-=⎨⎩≤<≤<则3()2f = .13.如图,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67,30,此时气球的高是46 m ,则河流的宽度BC 约等于m .(用四舍五入法将结果精确到个位.参考数据:sin670.92≈,cos670.39≈,sin370.60≈,cos370.80≈ 1.73≈)14.设m ∈R ,过定点A 的动直线0x my +=和过定点B 的动直线30mx y m --+=交于点(,)P x y ,则||||PA PB 的最大值是 .15.以A 表示值域为R 的函数组成的集合,B 表示具有如下性质的函数()x ϕ组成的集合:对于函数()x ϕ,存在一个正数M ,使得函数()x ϕ的值域包含于区间[,]M M -.例如,当31()x x ϕ=,2()sin x x ϕ=时,1()x A ϕ∈,2()x B ϕ∈.现有如下命题:①设函数()f x 的定义域为D ,则“()f x A ∈”的充要条件是“b ∀∈R ,a D ∃∈,()f a b =”; ②函数()f x B ∈的充要条件是()f x 有最大值和最小值;③若函数()f x ,()g x 的定义域相同,且()f x A ∈,()g x B ∈,则()()f x g x B +∉; ④若函数2()ln(2)1xf x a x x =+++(2x >-,a ∈R )有最大值,则()f xB ∈. 其中的真命题有 (写出所有真命题的序号).-------------在--------------------此--------------------卷--------------------上--------------------答--------------------题--------------------无--------------------效----------------姓名________________ 准考证号_____________三、解答题:本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤.16.(本小题满分12分)已知函数π()sin(3)4f x x=+.(Ⅰ)求()f x的单调递增区间;(Ⅱ)若α是第二象限角,4π()cos()cos2354fααα=+,求cos sinαα-的值.17.(本小题满分12分)一款击鼓小游戏的规则如下:每盘游戏都需击鼓三次,每次击鼓要么出现一次音乐,要么不出现音乐;每盘游戏击鼓三次后,出现一次音乐获得10分,出现两次音乐获得20分,出现三次音乐获得100分,没有出现音乐则扣除200分(即获得-200分).设每次击鼓出现音乐的概率为12,且各次击鼓出现音乐相互独立.(Ⅰ)设每盘游戏获得的分数为X,求X的分布列;(Ⅱ)玩三盘游戏,至少有一盘出现音乐的概率是多少?(Ⅲ)玩过这款游戏的许多人都发现,若干盘游戏后,与最初的分数相比,分数没有增加反而减少了.请运用概率统计的相关知识分析分数减少的原因. 18.(本小题满分12分)三棱锥A BCD-及其侧视图、俯视图如图所示.设M,N分别为线段AD,AB的中点,P为线段BC上的点,且MN NP⊥.(Ⅰ)证明:P为线段BC的中点;(Ⅱ)求二面角A NP M--的余弦值.19.(本小题满分12分)设等差数列{}na的公差为d,点(,)n na b在函数()2xf x=的图象上(n*∈N).(Ⅰ)若12a=-,点87(,4)a b在函数()f x的图象上,求数列{}na的前n项和nS;(Ⅱ)若11a=,函数()f x的图象在点22(,)a b处的切线在x轴上的截距为12ln2-,求数列{}nnab的前n项和nT.20.(本小题满分13分)已知椭圆C:22221x ya b+=(0)a b>>的焦距为4,其短轴的两个端点与长轴的一个端点构成正三角形.(Ⅰ)求椭圆C的标准方程;(Ⅱ)设F为椭圆C的左焦点,T为直线3x=-上任意一点,过F作TF的垂线交椭圆C于点P,Q.(ⅰ)证明:OT平分线段PQ(其中O为坐标原点);(ⅱ)当||||TFPQ最小时,求点T的坐标.21.(本小题满分14分)已知函数2()e1xf x ax bx=---,其中,a b∈R,e 2.71828=⋅⋅⋅为自然对数的底数.(Ⅰ)设()g x是函数()f x的导函数,求函数()g x在区间[0,1]上的最小值;(Ⅱ)若(1)0f=,函数()f x在区间(0,1)内有零点,求a的取值范围.数学试卷第4页(共18页)数学试卷第5页(共18页)数学试卷第6页(共18页)101{A B-=,【提示】由题意,可先化简集合【考点】交集及其运算32最大值,画出可行域如图:1x=⎧【解析】解:如图:31tan45tan30-︒-︒tan1560AD︒=,∴tan6060DC AD=︒=120(31)(m)-.数学试卷第7页(共18页)数学试卷第8页(共18页)数学试卷第9页(共18页)数学试卷 第10页(共18页) 数学试卷 第11页(共18页) 数学试卷 第12页(共18页)2OA OB =,∴12122x x y y +=,结合,B 位于x 轴的两侧,∴122y y =-,故不妨令点A 在轴上方,则0y >,又1123y y =. 面积之和的最小值是【提示】可先设直线方程和点的坐标,联立直线与抛物线的方程得到一个一元二次方程,再利用韦达定理及2OA OB =消元,最后将面积之和表示出来,探求最值问题【考点】直线与圆锥曲线的关系【答案】2【解析】(,2)c a b m m m =+=||||||||a c b ca cbc =,即2252051620525m m m =+++,即584m +=解得2m =.【提示】利用向量的坐标运算、数量积运算、向量的夹角公式即可得出.数学试卷 第13页(共18页) 数学试卷 第14页(共18页) 数学试卷 第15页(共18页)4cos sin 5α(﹣是第二象限角,∴cos α-ABAC A =1BC AA AC A =,,11BC ACC A ⊥平面AB 的中点M 1DEA MC 平面1DE A MC 平面231142434(1)44n nn n -++++-+2341142434(1)44n n n n +++++-+114(13)4443n n n n ++----⋅=,∴1(31)449n n n T +-+=. 是平行四边形,∴OP QT =,∴(1=±.2122242|||242333m y y m m -⎛⎫-=-= ⎪++⎝⎭. 22(,)Q x y .直线方程与椭圆方程可得根与系可得OP QT =,即可解得21|||y y -. 【考点】直线与圆锥曲线的综合问题数学试卷 第16页(共18页) 数学试卷 第17页(共18页) 数学试卷 第18页(共18页)11ln 2x x ⎫=-⎪⎭上单调递增,在区间。

四川省德阳五中2014-2015学年高二上学期第二次月考数学试卷一、选择题(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)设全集U={﹣2,﹣1,0,1,2},集合A={1,2},B={﹣2,1,2},则A∪(∁U B)等于()A.∅B.{1} C.{1,2} D.{﹣1,0,1,2}2.(5分)设φ∈R,则“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件3.(5分)若a∈{﹣2,0,1,},则方程x2+y2+ax+2ay+2a2+a﹣1=0表示的圆的个数为()A.0 B.1 C.2 D.34.(5分)如图所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是()A.45°B.60°C.90°D.120°5.(5分)已知函数f(x)=是(﹣∞,+∞)上的减函数,那么a的取值范围是()A.(0,3)B.(0,3] C.(0,2)D.(0,2]6.(5分)已知在m、n、l1、l2表示直线,α、β表示平面,若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是()A.m∥β且l1∥αB.m∥β且n∥βC.m∥β且n∥l2D.m∥l1且n∥l2 7.(5分)已知某几何体的三视图如图所示,则该几何体的体积为()A.B.32 C.D.+8.(5分)已知A,B,P是双曲线上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积,则该双曲线的离心率为()A.B.C.D.9.(5分)已知直线L:与曲线仅有三个交点,则实数m的取值范围是()A.B.C.D.10.(5分)在平面直角坐标系中,A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x ﹣4y≥0}则P={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为()A.6 B.6+πC.12+πD.18+π二、填空题(本大题共5小题,每小题5分)11.(5分)抛物线y=4x2的焦点坐标是.12.(5分)设等差数列{a n}的前9项和S9=18,则a1+a3+a11=.13.(5分)已知点A(2,﹣3),B(﹣3,﹣2),直线l过点P(1,1)且与线段AB有交点,则直线l的斜率k的取值范围为.14.(5分)正四棱锥S﹣ABCD的底面边长为2,高为2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为.15.(5分)下列命题中,正确的是.①平面向量与的夹角为60°,=(2,0),||=1,则|+|=②已知=(sinθ,),=(1,),其中θ∈,则⊥③O是△ABC所在平面上一定点,动点P满足:=+λ(+),λ∈(0,+∞),则直线AP一定通过△ABC的内心④双曲线﹣=1的左焦点为F1,顶点为A1、A2,P是双曲线上任意一点,则分别以线段PF1、A1A2为直径的两圆的位置关系为内切或外切;⑤命题“∃x∈R,x2﹣2x+4>0”的否定是“∀x∈R,x2﹣2x+4≤0”.三、解答题(本大题共75分,其中16、17、18、19题各12分,20题13分,21题14分)16.(12分)已知a>0,命题p:函数y=a x为减函数.命题q:当x∈[,2]时,函数f(x)=x+>恒成立,如果p或q为真命题,p且q为假命题,求a的取值范围.17.(12分)在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.(Ⅰ)求角A的大小;(Ⅱ)若△ABC的面积S=5,b=5,求sinBs in C的值.18.(12分)根据下列条件,分别求出相应椭圆的标准方程:(1)焦点在y轴上,长轴是短轴的3倍且经过点A(3,0);(2)已知一个焦点是F(1,0),且短轴的两个三等分点M,N与F构成正三角形.19.(12分)设数列{b n}的前n项和为S n,且b n=2﹣2S n;数列{a n}为等差数列,且a5=14,a7=20.(1)求数列{b n}的通项公式;(2)若c n=a n•b n(n=1,2,3…),T n为数列{c n}的前n项和.求T n.20.(13分)如图所示,圆柱的高为2,底面半径为,AE、DF是圆柱的两条母线,过AD 作圆柱的截面交下底面于BC.(1)求证:BC∥EF;(2)若四边形ABCD是正方形,求证B C⊥BE;(3)在(2)的条件下,求四棱锥A﹣BCE的体积.21.(14分)设椭圆C:的右、右焦点分别为F1、F2,上顶点为A,过A与AF2垂直的直线交x轴负半轴于Q点,且2+=0.(1)求椭圆C的离心率;(2)若过A、Q、F2三点的圆恰好与直线x﹣y﹣3=0相切,求椭圆C的方程;(3)在(2)的条件下,过右焦点F2的直线交椭圆于M、N两点,点P(4,0),求△PM N面积的最大值.四川省德阳五中2014-2015学年高二上学期第二次月考数学试卷参考答案与试题解析一、选择题(本大题共10小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.(5分)设全集U={﹣2,﹣1,0,1,2},集合A={1,2},B={﹣2,1,2},则A∪(∁U B)等于()A.∅B.{1} C.{1,2} D.{﹣1,0,1,2}考点:交、并、补集的混合运算.专题:计算题.分析:先求出集合B的补集,再根据两个集合的并集的意义求解即可.解答:解:∵全集U={﹣2,﹣1,0,1,2},集合A={1,2},B={﹣2,1,2},∴C U B={﹣1,0},A∪(C U B)={﹣1,0,1,2},故选:D.点评:本题主要考查了交、并、补集的混合运算,是集合并集的基础题,也是2015届高考常会考的题型.2.(5分)设φ∈R,则“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的()A.充分而不必要条件B.必要而不充分条件C.充分必要条件D.既不充分也不必要条件考点:必要条件、充分条件与充要条件的判断;函数奇偶性的判断.专题:简易逻辑.分析:直接把φ=0代入看能否推出是偶函数,再反过来推导结论即可.解答:解:因为φ=0时,f(x)=cos(x+φ)=cosx是偶函数,成立;但f(x)=cos(x+φ)(x∈R)为偶函数时,φ=kπ,k∈Z,推不出φ=0.故“φ=0”是“f(x)=cos(x+φ)(x∈R)为偶函数”的充分而不必要条件.故选:A.点评:判断充要条件的方法是:①若p⇒q为真命题且q⇒p为假命题,则命题p是命题q的充分不必要条件;②若p⇒q为假命题且q⇒p为真命题,则命题p是命题q的必要不充分条件;③若p⇒q为真命题且q⇒p为真命题,则命题p是命题q的充要条件;④若p⇒q为假命题且q⇒p为假命题,则命题p是命题q的即不充分也不必要条件.⑤判断命题p与命题q所表示的范围,再根据“谁大谁必要,谁小谁充分”的原则,判断命题p与命题q的关系.3.(5分)若a∈{﹣2,0,1,},则方程x2+y2+ax+2ay+2a2+a﹣1=0表示的圆的个数为()A.0 B.1 C.2 D.3考点:圆的标准方程.专题:直线与圆.分析:方程即(x﹣)2+(y+a)2=1﹣a﹣a2 ,把a的值逐一代入检验,可得结论.解答:解:方程x2+y2+ax+2ay+2a2+a﹣1=0 即方程(x﹣)2+(y+a)2=1﹣a﹣a2 ,可以表示以(,﹣a)为圆心、半径为的圆.当a=﹣2时,圆心(1,2)、半径为0,不表示圆.当a=0时,圆心(0,0)、半径为1,表示一个圆.当a=1时,圆心(,﹣1)、1﹣a﹣a2<0,不表示圆.当a=时,圆心(,﹣)、1﹣a﹣a2<0,不表示圆.综上可得,所给的方程表示的圆的个数为1,故选:B.点评:本题主要考查圆的标准方程的特征,属于基础题.4.(5分)如图所示,在三棱柱ABC﹣A1B1C1中,AA1⊥底面ABC,AB=BC=AA1,∠ABC=90°,点E、F分别是棱AB、BB1的中点,则直线EF和BC1所成的角是()A.45°B.60°C.90°D.120°考点:异面直线及其所成的角.专题:计算题.分析:先将EF平移到AB1,再利用中位线进行平移,使两条异面直线移到同一点,得到所成角,求之即可.解答:解:连接AB1,易知AB1∥EF,连接B1C交BC1于点G,取AC的中点H,连接GH,则GH∥AB1∥EF.设AB=BC=AA1=a,连接HB,在三角形GHB中,易知GH=HB=GB=a,故两直线所成的角即为∠HGB=60°.故选B点评:本题主要考查了异面直线及其所成的角,平移法是研究异面直线所成的角的最常用的方法,属于基础题.5.(5分)已知函数f(x)=是(﹣∞,+∞)上的减函数,那么a的取值范围是()A.(0,3)B.(0,3] C.(0,2)D.(0,2]考点:分段函数的应用.专题:计算题;函数的性质及应用.分析:由条件可得,a﹣3<0①,2a>0②,(a﹣3)×1+5≥2a③,求出它们的交集即可.解答:解:由于函数f(x)=是(﹣∞,+∞)上的减函数,则x≤1时,是减函数,则a﹣3<0①x>1时,是减函数,则2a>0②由单调递减的定义可得,(a﹣3)×1+5≥2a③由①②③解得,0<a≤2.故选D.点评:本题考查分段函数的性质和运用,考查函数的单调性和运用,注意各段的单调性,以及分界点的情况,属于中档题和易错题.6.(5分)已知在m、n、l1、l2表示直线,α、β表示平面,若m⊂α,n⊂α,l1⊂β,l2⊂β,l1∩l2=M,则α∥β的一个充分条件是()A.m∥β且l1∥αB.m∥β且n∥βC.m∥β且n∥l2D.m∥l1且n∥l2考点:平面与平面平行的判定;必要条件、充分条件与充要条件的判断.专题:计算题.分析:根据题意,要使α∥β,只要一个平面内有两条相交直线和另一个平面平行即可.解答:解:由题意得,m、n 是平面α内的两条直线,l1、l2是平面β内的两条相交直线,要使α∥β,只要一个平面内有两条相交直线和另一个平面平行即可,故选 D.点评:本题考查两个平面平行的判定定理的应用,明确已知条件的含义是解题的关键.7.(5分)已知某几何体的三视图如图所示,则该几何体的体积为()A.B.32 C.D.+考点:由三视图求面积、体积.专题:计算题.分析:由几何体的三视图知,分析可得该几何体的形状,进而分为两个棱锥,分别求出其体积并相加就能求出该几何体的体积.解答:解:由几何体的三视图知,该几何体是如图所示的几何体,其体积V=V F﹣ABC+V A﹣CDEF,三棱锥F﹣ABC中底面是等腰直角三角形,FC⊥面ABCD,FC=4,∴该几何体的体积V==,同理四棱锥A﹣CDEF的体积V A﹣CDEF=×(×6×4)×4=16,几何体的体积为故选C.点评:本题考点是由三视图求几何体的面积、体积,考查对三视图的理解与应用,主要考查三视图与实物图之间的关系,用三视图中的数据还原出实物图的数据,再根据相关的公式求表面积与体积,本题求的是三棱锥的体积.三视图的投影规则是:“主视、俯视长对正;主视、左视高平齐,左视、俯视宽相等”.三视图是2015届高考的新增考点,不时出现在2015届高考试题中,应予以重视.8.(5分)已知A,B,P是双曲线上不同的三点,且A,B连线经过坐标原点,若直线PA,PB的斜率乘积,则该双曲线的离心率为()A.B.C.D.考点:双曲线的简单性质;直线的斜率.专题:计算题.分析:根据双曲线的对称性可知A,B关于原点对称,设出A,B和P的坐标,把A,B点坐标代入双曲线方程可求得直线PA和直线PB的斜率之积,进而求得a和b的关系,进而根据a,b和c的关系求得a和c的关系即双曲线的离心率.解答:解:根据双曲线的对称性可知A,B关于原点对称,设A(x1,y1),B(﹣x1,﹣y1),P(x,y),则,,.故选D点评:本题主要考查了双曲线的简单性质.涉及了双曲线的对称性质,考查了学生对双曲线基础知识的全面掌握.9.(5分)已知直线L:与曲线仅有三个交点,则实数m的取值范围是()A.B.C.D.考点:直线与圆锥曲线的关系.专题:数形结合.分析:分析曲线C的方程可得是椭圆的上半部分与双曲线的上半部分,由图形可得找出两个临界值即直线平移到(0,1)与直线和椭圆相切(△=16m2﹣8(4m2﹣4)=0)的时候,得到答案.解答:解:由题意得曲线∴即4y2=|4﹣x2|(y≥0)当4﹣x2≥0时得到4y2=4﹣x2即当4﹣x2<0时得到由以上可得曲线C的图形为∵直线L:与双曲线的渐近线平行∴把直线向上平移平移到(0,1)点时有两个交点,此时m=1.继续向上平移则有3个交点.当直线与椭圆的上半部分相切时此时有两个交点.联立直线与椭圆的方程代入整理得2x2+4mx+4m2﹣4=0△=16m2﹣8(4m2﹣4)=0即(舍去)由图示可得由以上可得1<m<故答案为C.点评:解决此类问题的根据是灵活运用平面几何的相关知识与结论,结合图形解决问题,即数形结合的是想是高中数学的一个重点也是2015届高考必考的知识点.10.(5分)在平面直角坐标系中,A={(x,y)|x2+y2≤1},B={(x,y)|x≤4,y≥0,3x ﹣4y≥0}则P={(x,y)|x=x1+x2,y=y1+y2,(x1,y1)∈A,(x2,y2)∈B}所表示的区域的面积为()A.6 B.6+πC.12+πD.18+π考点:简单线性规划.专题:不等式的解法及应用.分析:把x=x1+x2,y=y1+y2,中的x1,y1代入x2+y2≤1,可得点集Q的轨迹方程,然后求出点Q所表示的区域的面积.解答:解:由x=x1+x2,y=y1+y2,得x1=x﹣x2,y1=y﹣y2,∵(x1,y1)∈A,∴把x1=x﹣x2,y1=y﹣y2,代入x2+y2≤1,∴(x﹣x2)2+(y﹣y2)2≤1点集Q所表示的区域是以集合B={(x,y)|x≤4,y≥0,3x﹣4y≥0},的区域的边界为圆心轨迹半径为1 的圆内部分,如图,其面积为:5+6+4+3+π=18+π故选:D.点评:本题考查二元一次不等式组与平面区域的关系问题,考查转化数学思想,作图能力,难度较大.二、填空题(本大题共5小题,每小题5分)11.(5分)抛物线y=4x2的焦点坐标是.考点:抛物线的简单性质.专题:计算题.分析:先化简为标准方程,进而可得到p的值,即可确定答案.解答:解:由题意可知∴p=∴焦点坐标为故答案为点评:本题主要考查抛物线的性质.属基础题.12.(5分)设等差数列{a n}的前9项和S9=18,则a1+a3+a11=6.考点:等差数列的前n项和.专题:等差数列与等比数列.分析:由S9=18和求和公式以及性质可得a5=2,再由性质可得a1+a3+a11=3a5,代值计算可得.解答:解:∵等差数列{a n}的前9项和S9=18,∴S9=9•=9•=9a5=18,∴a5=2,∴a1+a3+a11=a3+(a1+a11)=a3+(a5+a7)=a5+(a3+a7)=a5+2a5=3a5=3×2=6故答案为:6点评:本题考查等差数列的求和公式和等差数列的性质,转化为a5是解决问题的关键,属中档题.13.(5分)已知点A(2,﹣3),B(﹣3,﹣2),直线l过点P(1,1)且与线段AB有交点,则直线l的斜率k的取值范围为(﹣∞,﹣4]∪[,+∞).考点:直线的斜率.专题:直线与圆.分析:由题意画出图形,求出PA和PB的斜率,数形结合得答案.解答:解:如图,,.∴直线l的斜率k的取值范围为(﹣∞,﹣4]∪[,+∞).故答案为:(﹣∞,﹣4]∪[,+∞).点评:本题考查了直线的斜率,考查了数形结合的解题思想方法,是中档题.14.(5分)正四棱锥S﹣ABCD的底面边长为2,高为2,E是边BC的中点,动点P在表面上运动,并且总保持PE⊥AC,则动点P的轨迹的周长为.考点:点、线、面间的距离计算.专题:计算题.分析:根据题意可知点P的轨迹为三角形EFG,其中G、F为中点,根据中位线定理求出EF、GE、GF,从而求出轨迹的周长.解答:解:由题意知:点P的轨迹为如图所示的三角形EFG,其中G、F为中点,∴EF=BD=,GE=GF=SB=,∴轨迹的周长为+.答案:+点评:本题主要考查了轨迹问题,以及点到面的距离等有关知识,同时考查了空间想象能力,计算推理能力,属于中档题.15.(5分)下列命题中,正确的是①②③④⑤..①平面向量与的夹角为60°,=(2,0),||=1,则|+|=②已知=(sinθ,),=(1,),其中θ∈,则⊥③O是△ABC所在平面上一定点,动点P满足:=+λ(+),λ∈(0,+∞),则直线AP一定通过△ABC的内心④双曲线﹣=1的左焦点为F1,顶点为A1、A2,P是双曲线上任意一点,则分别以线段PF1、A1A2为直径的两圆的位置关系为内切或外切;⑤命题“∃x∈R,x2﹣2x+4>0”的否定是“∀x∈R,x2﹣2x+4≤0”.考点:命题的真假判断与应用.专题:简易逻辑.分析:①由模的计算公式|+|==,即可得出;②由=sinθ+=sinθ﹣sinθ=0,可得⊥;③O是△ABC所在平面上一定点,动点P满足:=+λ(+),λ∈(0,+∞),由正弦定理可得:,,可得与∠BAC的平分线共线;④双曲线﹣=1的左焦点为F1,顶点为A1、A2,P是双曲线上任意一点,假设点P在双曲线上的左支,F2为双曲线的右焦点,线段PF1的中点为O1,连接OO1,可得|OO1|===a+,此时⊙O与⊙O1外切;同理当点P在双曲线的右支上,两圆内切时,即可判断出;⑤利用命题的否定定义即可判断出.解答:解:①平面向量与的夹角为60°,=(2,0),||=1,则|+|===,正确;②∵,=sinθ+=sinθ﹣sinθ=0,∴⊥,正确;③O是△ABC所在平面上一定点,动点P满足:=+λ(+),λ∈(0,+∞),∴=λ(+),由正弦定理可得:,∴,∴与∠BAC的平分线共线,则直线AP一定通过△ABC的内心,正确;④双曲线﹣=1的左焦点为F1,顶点为A1、A2,P是双曲线上任意一点,假设点P在双曲线上的左支,F2为双曲线的右焦点,线段PF1的中点为O1,连接OO1,则|OO1|===a+,此时⊙O与⊙O1外切;同理当点P在双曲线的右支上,两圆内切时,因此分别以线段PF1、A1A2为直径的两圆的位置关系为内切或外切,正确;⑤命题“∃x∈R,x2﹣2x+4>0”的否定是“∀x∈R,x2﹣2x+4≤0”,正确.综上可得:①②③④⑤都正确.故答案为:①②③④⑤.点评:本题考查了简易逻辑的判定、向量的模的计算公式、向量垂直与数量积的关系、三角形的内心的向量表示、双曲线的性质、两圆的位置关系,考查了推理能力与计算能力,属于难题.三、解答题(本大题共75分,其中16、17、18、19题各12分,20题13分,21题14分)16.(12分)已知a>0,命题p:函数y=a x为减函数.命题q:当x∈[,2]时,函数f(x)=x+>恒成立,如果p或q为真命题,p且q为假命题,求a的取值范围.考点:复合命题的真假.专题:简易逻辑.分析:由a>0,命题p:函数y=a x为减函数.可得0<a<1.命题q:当x∈[,2]时,函数f(x)=x+>恒成立,可得,利用基本不等式即可得出.由p或q为真命题,p且q为假命题,可得p,q中必然一个真命题一个为假命题.解出即可.解答:解:由a>0,命题p:函数y=a x为减函数.∴0<a<1.命题q:当x∈[,2]时,函数f(x)=x+>恒成立,∴,∵x∈[,2]时,函数f(x)=x+=2,当且仅当x=1时取等号.∴,又a>0,∴.∵p或q为真命题,p且q为假命题,∴p,q中必然一个真命题一个为假命题.①当p真q假时,,解得,a的取值范围是.②当q真p假时,,解得a≥1,a的取值范围是[1,+∞).点评:本题考查了指数函数的单调性、基本不等式、不等式组的解法、“或”“且”“非”命题的真假的判断等基础知识,考查了分类讨论的思想方法,考查了推理能力和计算能力,属于难题.17.(12分)在△ABC中,角A,B,C对应的边分别是a,b,c,已知cos2A﹣3cos(B+C)=1.(Ⅰ)求角A的大小;(Ⅱ)若△ABC的面积S=5,b=5,求sinBsinC的值.考点:余弦定理;正弦定理.专题:解三角形.分析:(I)利用倍角公式和诱导公式即可得出;(II)由三角形的面积公式即可得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,即可得出a.又由正弦定理得即可得到即可得出.解答:解:(Ⅰ)由cos2A﹣3cos(B+C)=1,得2cos2A+3cosA﹣2=0,即(2cosA﹣1)(cosA+2)=0,解得(舍去).因为0<A<π,所以.(Ⅱ)由S===,得到bc=20.又b=5,解得c=4.由余弦定理得a2=b2+c2﹣2bccosA=25+16﹣20=21,故.又由正弦定理得.点评:熟练掌握三角函数的倍角公式和诱导公式、三角形的面积公式、余弦定理得、正弦定理是解题的关键.18.(12分)根据下列条件,分别求出相应椭圆的标准方程:(1)焦点在y轴上,长轴是短轴的3倍且经过点A(3,0);(2)已知一个焦点是F(1,0),且短轴的两个三等分点M,N与F构成正三角形.考点:椭圆的标准方程.专题:圆锥曲线的定义、性质与方程.分析:首先设出椭圆的方程然后根据题中的相关量的关系求出具体的a和b,进一步确定方程.解答:解(1)因椭圆的焦点在y轴上,设其方程为:(a>b>0)∵椭圆过点A(3,0)∴∴b=3又2a=3•2b∴a=9∴方程为(2)由△FMN为正三角形则c=|OF|=|MN|=×b=1∴b=a2=b2+c2=4故椭圆方程为:故答案为:(1)(2)点评:本题考查的知识点:椭圆的方程,椭圆中a、b、c的关系运算.19.(12分)设数列{b n}的前n项和为S n,且b n=2﹣2S n;数列{a n}为等差数列,且a5=14,a7=20.(1)求数列{b n}的通项公式;(2)若c n=a n•b n(n=1,2,3…),T n为数列{c n}的前n项和.求T n.考点:等差数列与等比数列的综合.专题:计算题.分析:(1)由已知条件b n=2﹣2S n;当n=1时先求出,再利用b n﹣b n﹣1=﹣2(S n﹣S n ﹣1)=﹣2bn得到{b n}是以为首项,为公比的等比数列,利用等比数列的通项公式求出通项.(2)求出,是一个等差数列与一个等比数列的乘积,所以利用错位相减的方法求出和.解答:解:(1)由b n=2﹣2S n,令n=1,则b1=2﹣2S1,又S1=b1所以…(2分)当n≥2时,由b n=2﹣2S n,可得b n﹣b n﹣1=﹣2(S n﹣S n﹣1)=﹣2b n即…(4分)所以{b n}是以为首项,为公比的等比数列,于是…(6分)(2)数列{a n}为等差数列,公差,可得a n=3n﹣1…(7分)从而∴,∴…(11分).…(12分)点评:求一个数列的前n项和,应该先求出数列的通项,根据通项的特点选择合适的求和方法.20.(13分)如图所示,圆柱的高为2,底面半径为,AE、DF是圆柱的两条母线,过AD 作圆柱的截面交下底面于BC.(1)求证:BC∥EF;(2)若四边形ABCD是正方形,求证BC⊥BE;(3)在(2)的条件下,求四棱锥A﹣BCE的体积.考点:直线与平面垂直的性质;棱柱、棱锥、棱台的体积;空间中直线与直线之间的位置关系.专题:计算题.分析:(1)在圆柱中:由上底面∥下底面,知BC∥AD,由AE、DF是圆柱的两条母线,知ADFE是平行四边形,由此能够证明BC∥EF.(2)由AE是圆柱的母线,知AE⊥下底面,由BC⊂下底面,知AE⊥B C.由此入手能够证明BC⊥BE.(3)因为母线AE垂直于底面,所以AE是三棱锥A﹣BCE的高,EO就是四棱锥E﹣ABCD的高.设正方形ABCD的边长为x,则AB=EF=x,,由此利用题设条件,能够求出四棱锥A﹣BCE的体积.解答:(本题满分14分)(1)证明:在圆柱中:∵上底面∥下底面,且上底面∩截面ABCD=AD,下底面∩截面ABCD=BC,∴BC∥AD….(2分)又∵AE、DF是圆柱的两条母线,∴,∴ADFE是平行四边形,所以AD∥EF,又BC∥AD∴BC∥EF….(5分)(2)∵AE是圆柱的母线,∴AE⊥下底面,又BC⊂下底面,∴AE⊥BC….(7分)又∵截面ABCD是正方形,所以BC⊥AB,又AB∩AE=A,∴BC⊥面ABE,又BE⊂面ABE,∴BC⊥BE…(9分)(3)因为母线AE垂直于底面,所以AE是三棱锥A﹣BCE的高…(10分),EO就是四棱锥E﹣ABCD的高…(10分)设正方形ABCD的边长为x,则AB=EF=x,又∵BC∥EF,且BC⊥BE,∴EF⊥BE,∴BF为直径,即BF=在Rt△BEF中,BF2=BE2+EF2即,∴S ABCD=4×4=16,…(12分),∴.∴四棱锥A﹣BCE的体积===.…(14分)点评:本题考查直线平行和直线垂直的证明,考查棱锥的体积的求法.解题时要认真审题,仔细解答,注意合理地化空间问题为平面问题.21.(14分)设椭圆C:的右、右焦点分别为F1、F2,上顶点为A,过A与AF2垂直的直线交x轴负半轴于Q点,且2+=0.(1)求椭圆C的离心率;(2)若过A、Q、F2三点的圆恰好与直线x﹣y﹣3=0相切,求椭圆C的方程;(3)在(2)的条件下,过右焦点F2的直线交椭圆于M、N两点,点P(4,0),求△PMN面积的最大值.考点:直线与圆锥曲线的综合问题.专题:计算题.分析:(1)欲求椭圆C的离心率,只需得到关于a,c的齐次式,由,2+=0,以及b2=a2﹣c2,就可得到a,c的齐次式,求出椭圆C的离心率.(2)带着参数求出过A、Q、F2三点的圆的圆心坐标以及半径,再根据圆恰好与直线x﹣y ﹣3=0相切,求出参数的值,就可得到椭圆C的方程.(3)设直线MN的方程,欲(2)中求出的椭圆方程联立,求出y1+y2,y1y2的值,就可得到|y1﹣y2|,而△PMN的面积可用=|PF2|•|y1﹣y2|表示,再利用均值不等式求出最大值.解答:解:(1)设Q(x0,0).∵F2(c,0),A(0,b),∴=(﹣c,b),=(x0,﹣b)∵,∴﹣cx0﹣b2=0,故 x0=﹣,又∵2+=0,∴F1为F2Q的中点,故﹣2c=﹣+c,即,b2=3c2=a2﹣c2,∴e==(2)∵e==,∴a=2c,b=c,则F2(c,0),Q(﹣3c,0),A(0,c)∴△AQF2的外接圆圆心(﹣c,0),半径r=|F2Q|=a=2c∴=2c,解得c=1,∴a=2,b=椭圆C的方程为(3)设直线MN:x=my+1,代入,得,(3m2+4)y2+6my﹣9=0设M(x1,y1),n(x2,y2),∴y1+y2=﹣,y1y2=﹣,|y1﹣y2|==∴S△PMN=|PF2|•|y1﹣y2|=,令=λ≥,∴S△PMN==≤=∴△PMN面积的最大值为,此时,m=0点评:本题考查了椭圆离心率,方程的求法,以及直线与椭圆位置关系的判断,注意设而不求思想的应用.。

德阳市高中2015级“二诊”考试数学试卷(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.已知i 为虚数单位,实数x ,y 满足(2)x i i y i ,则xyi ()A .1B .2 C.3 D.52.已知集合2{|40}A x N x x,集合2{|20}B x xx a,若{1,2,3,3}A B ,则AB()A .{1}B .{2} C.{3} D.3.函数()sin(2)f x x 的图象向右平移6个单位后所得的图象关于原点对称,则可以是()A .6B.3C .4D .234.实验测得四组数对(,)x y 的值为(1,2),(2,5),(4,7),(5,10),则y 与x 之间的回归直线方程是()A .1.80.6y x B.1.80.6y x C .1.52.5y x D .0.57.5y x 参考公式:121()()()nii i nii x x y y bx x ,ay bx .5.如图所示的三视图表示的几何体的体积为323,则该几何体的外接球的表面积为()A .12B.24C.36D.486.《九章算术》是我国古代一部数学名著,某数学爱好者阅读完其相关章节后编制了如图的程序框图,其中(,)MOD m n 表示m 除以n 的余数,例如(7,3)1MOD .若输入m 的值为8时,则输出i 的值为()A .2B .3C .4D .57.已知235log log log 0xy z,则2x、3y、5z 的大小排序为()A .235xyzB .325yxzC .523zxyD .532zyx8.以等腰直角三角形ABC 的斜边BC 上的中线AD 为折痕,将ABD 与ACD 折成互相垂直的两个平面,得到以下四个结论:①BD平面ACD ;②ABC 为等边三角形;③平面ADC 平面ABC ;④点D 在平面ABC 内的射影为ABC 的外接圆圆心.其中正确的有()A .①②③B .②③④ C.①②④ D .①③④9. 已知双曲线22221(0,0)x y a b ab的离心率为2,其一条渐近线被圆22()4(0)x m ym截得的线段长为22,则实数m 的值为()A .3B .1 C.2 D.210.已知函数()sin f x x x ,若[2,1]x,使得2()()0f xx f x k 成立,则实数k 的取值范围是()A .[1,3] B.[0,3] C .(,3] D .[0,)11. 如图,过抛物线24yx 的焦点F 作倾斜角为的直线l ,l 与抛物线及其准线从上到下依次交于A 、B 、C 点,令1AF BF,2BC BF,则当3时,12的值为()A .3B .4C .5D .612. 已知A 、B 是函数2,()()(2),()x aex a f x f a x xa (其中常数0a )图象上的两个动点,点(,0)P a ,若PA PB 的最小值为0,则函数()f x 的最大值为()A .21eB .1eC .2e eD .e e第Ⅱ卷(非选择题共90分)二、填空题:共4小题,每小题5分,共20分.将答案填在答题卡上.13.已知实数x ,y 满足条件2300xy x y x y,则3xy 的最大值为.14.为弘扬我国优秀的传统文化,某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则y x的值为.15.如图,在三角形OPQ 中,M 、N 分别是边OP 、OQ 的中点,点R 在直线MN 上,且OR xOP yOQ (,)x yR ,则代数式22xy 的最小值为.16.已知ABC 中,角A 、B 、C 所对的边分别是a 、b 、c 且6a,4sin 5sin B C ,2A C ,若O 为ABC 的内心,则ABO 的面积为.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知数列{}n a 满足11a ,121nna a .(1)求证:数列{1}na 为等比数列;(2)求数列12nn na a 的前n 项和n T .18.省环保厅对A 、B 、C 三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:A 城B 城C 城优(个)28 xy良(个)3230z已知在这180个数据中随机抽取一个,恰好抽到记录B 城市空气质量为优的数据的概率为0.2.(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在C 城中应抽取的数据的个数;(2)已知23y ,24z ,求在C 城中空气质量为优的天数大于空气质量为良的天数的概率.19.如图,在四棱锥P ABCD 中,底面ABCD 为菱形,60DAB ,PD 平面ABCD ,2PD AD ,点E 、F 分别为AB 和PD 的中点.(1)求证:直线//AF 平面PEC ;(2)求点A 到平面PEC 的距离.20.已知椭圆C :22221(0)x y a b ab的两个焦点与短轴的一个端点构成的三角形的面积为23,且椭圆C 的离心率为32.(1)求椭圆C 的方程;(2)过点(4,0)且斜率不为零的直线l 与椭圆C 交于两点M 、N ,点(22,0)T ,试探究:直线MT 与NT 的斜率之积是否为常数.21.已知函数2()ln f x x mxx .(1)若12x是()f x 的一个极值点,求()f x 的最大值;(2)若121,,x x e e,12x x ,都有2112()()x f x x f x 1221()x x x x ,求实数m 的取值范围.请考生在22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一题记分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.22.在平面直角坐标系xOy 中,直线l :22x t yt(t 为参数),以坐标原点为极点,x 轴正半轴为极轴,建立极坐标系,曲线C :2sin.(1)求直线l 的极坐标方程及曲线C 的直角坐标方程;(2)记射线0,02与直线l 和曲线C 的交点分别为点M 和点N (异于点O ),求ON OM的最大值.23.已知函数()1f x x .(1)解关于x 的不等式2()1f x x ;(2)若关于x 的不等式2()1f x a xx 的解集非空,求实数a 的取值范围.德阳市高中2015级“二诊”试题数学参考答案(文史类)一、选择题1-5: DABAC 6-10: BACDA 11、12:CB二、填空题13. 8 14.3515.2416.7三、解答题17.解:(1)∵121nn a a ,∴112(1)nn a a .又11a ,∴1120a ,10n a .∴{1}na 是以2为首项,2为公比的等比数列.(2)由(1)知21nna ,∴1122(21)(21)nnnnn na a 1112121nn ,∴22111212121nT 31111212121nn 11121n .18.解:(1)由题意得0.2180x ,即36x .∴1802832363054yz ,∴在C 城中应抽取的数据个数为30549180. (2)由(1)知54y z ,,y z N 且23y,24z,∴满足条件的数对(,)y z 可能的结果有(23,31),(24,30),(25,29),(26,28),(27,27),(28,26),(29,25),(30,24)共8种.其中“空气质量为优的天数大于空气质量为良的天数”对应的结果有(28,26),(29,25),(30,24)共3种.∴在C 城中空气质量为优的天数大于空气质量为良的天数的概率为38.19.解:(1)取PC 的中点Q ,连结EQ 、FQ ,由题意,//FQ DC 且12FQ CD ,//AE CD 且12AECD ,故//AE FQ 且AEFQ ,所以,四边形AEQF 为平行四边形,所以,//AF EQ ,又EQ 平面PEC ,AF平面PEC ,所以,//AF 平面PEC .(2)设点A 到平面PEC 的距离为d . 由题意知在EBC 中,222cos EC EB BCEB BC EBC11421272,在PDE 中227PE PD DE ,在PDC 中2222PCPDCD,故EQPC ,5EQ AF,1225102PECS,131322AECS,所以由APECPAECV V 得:113102332d,解得3010d.20.解:(1)由题意得2332bcc a(其中c 椭圆的半焦距),解得2282a b.所以椭圆C 的方程为:22182xy. (2)由题意设直线l 的方程为:4xmy,11(,)M x y ,22(,)N x y ,由224182xmy x y得:22(4)880mymy ,所以1221222284846432(4)0m y y m y y mmm,故1212()8x x m y y 2324m,21212124()x x m y y m y y 22648164m m,MT NTk k 1212(22)(22)y y x x 12121222()8y y x x x x 3224(常数).21.解:(1)1'()21(0)f x mx x x,由题意得1'02f ,即210m ,所以1m,所以1'()21f x x x(21)(1)x x x,当102x时,'()0f x ;当12x时,'()0f x ,所以()f x 在10,2上单调递增,在1,2上单调递减.所以max1()2f x f3ln 24.(2)由题意得121,,x x e e,12x x 都有2112()()x f x x f x 1221()x x x x 111()f x x x 222()f x x x ,令函数()()f xg x xx2ln x mx xxxln 1x mx x x ,当12x x 时,()g x 在1,e e上单调递增,所以21ln '()10x g x m x在1,e e上恒成立,即21ln 1x m x在1,e e上恒成立,令21ln ()x h x x,1,xe e,则332ln '()0x h x x,所以()h x 在1,e e上单调递减,故min()()0h x h e ,所以实数m 的取值范围为(,1]. 同理,当12x x 时,()g x 在1,e e上单调递减,所以21ln '()10x g x m x在1,ee上恒成立,即21ln 1x m x在1,e e上恒成立,令21ln ()x h x x,1,xe e,则332ln '()0x h x x,所以()h x 在1,e e上单调递减,故2max1()2h x h e e.所以实数m 的取值范围为2[21,)e ,综上,实数m 的取值范围为2(,1][21,)e .22.解:(1)由题意得直线l 的普通方程为:4x y ,所以其极坐标方程为:4sin cos . 由2sin 得:22sin ,所以222xy y ,所以曲线C 的直角坐标方程为:2220x y y .(2)由题意2sin ON,4sin cosOM ,所以2sin sin cos 2ONOM 21sin 2444,由于02,所以当38时,ON OM取得最大值:214. 23.解:(1)由题意2()1f x x 211x x 211x x 或211x x ,所以220xx 或20x x ,即2x 或1x ,或1x 或0x ,故原不等式的解集为{|01}x x x 或. (2)2()1f x a x x 211ax x x ,由于211x x x 2222,12,112,1x x x x x x x x ,所以当1x时,211x x x 的最小值为-1. 所以实数a 的取值范围为:(1,).。

德阳市高中2021级质量监测考试(二)数学试卷(理工农医类)说明:1.本试卷分第Ⅰ卷和第Ⅱ卷,共4页,考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效.考试结束后,将答题卡交回,2.本试卷满分150分,120分钟完卷.第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若1=+z ,则2zz =-()A.12B.1C.D.22.已知集合{}260A x x x =--≤,10ln B xx ⎧⎫=≥⎨⎬⎩⎭,则A B = ()A.{}12x x <≤B.{}12x x ≤≤C.{}13x x <≤ D.{}13x x ≤≤3.若x ,y 满足约束条件2202201x y x y y +-≥⎧⎪--≤⎨⎪≤⎩,则43z x y =+的最大值为()A.19B.13C.9D.54.已知()9,A m 为抛物线C :22y px =(0p >)上一点,点A 到C 的焦点的距离为12,则p =()A.2B.3C.6D.95.质数(prime number )又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则这个数为质数,数学上把相差为2的两个素数叫做“孪生素数”.如:3和5,5和7……,在1900年的国际数学大会上,著名数学家希尔伯特提出了23个问题,其中第8个就是大名鼎鼎的孪生素数猜想:即存在无穷多对孪生素数.我国著名数学家张益唐2013年在《数学年刊》上发表论文《素数间的有界距离》,破解了困扰数学界长达一个半世纪的难题,证明了孪生素数猜想的弱化形式.那么,如果我们在不超过30的自然数中,随机选取两个不同的数,记事件A ,这两个数都是素数;事件B :这两个数不是孪生素数,则()P B A =()A.1115B.3745C.1315D.41456.一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积为()A.32π12a B.32π24a C.33π12a D.3π24a 7.已知各项不相等的等比数列{}n a 的前n 项和为n S ,若534S S -=,5678a a a =,则1a =()A.116-B.116C.64- D.648.已知函数()f x 的定义域为R ,且满足()()cos 222xxf x x ϕ-=++-,则“sin 1ϕ=”是“()f x 是奇函数”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件9.已知平面向量a ,b ,c 满足1a b == ,2c = ,若b ,c共线,且a b c ++= ,则a b c +-=()A.B.C.D.10.已知双曲线C :22221x y a b -=(0a >,0b >),O 为坐标原点,F 为C 的右焦点,以F为圆心,OF 为半径的圆与C 的渐近线在第一象限的交点为A ,若OAF △的面积为22a ,则双曲线的离心率为()A.B.C.72D.211.若函数()13f x x m x x=++-在[)2,+∞上单调递增,则实数m 的取值范围是()A.3,4⎛⎤-∞ ⎥⎝⎦B.8,9∞⎛⎤- ⎥⎝⎦C.38,49⎡⎤⎢⎥⎣⎦D.83,94⎡⎤-⎢⎥⎣⎦12.已知三棱锥-P ABC 的三条侧棱PA 、PB 、PC 两两互相垂直,O 是ABC 的垂心.若1OBC S =△,4ABC S = ,则PBC S =△()A.85B.2C.52D.第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分,第13~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.二、填空题:共4小题,每小题5分,共20分.将答案填在答题卡上.13.在()()6311x x -+的展开式中,3x 的系数为______.14.已知数列{}n a 满足11a =,且对任意*n ∈N ,有()11nn n a a n +=+-⋅,则22a =______.15.已知函数()ln ln f x a x bx =⋅-在1x =处取得极大值,则ba的取值范围是______.16.已知正实数x ,y ,z 满足26x xy yz xz x z +++++=,则32x y z ++的最小值是______.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且sin cos 32c BC =,3b =.(1)求B ;(2)若ABC 为锐角三角形,求ABC 的面积范围.18.轻食是餐饮的一种形态、轻的不仅仅是食材分量,更是食材烹饪方式简约,保留食材本来的营养和味道,近年来随着消费者健康意识的提升及美颜经济的火热,轻食行业迎来快速发展.某传媒公司为了获得轻食行业消费者行为数据,对中国轻食消费者进行抽样调查.统计其中400名中国轻食消费者(表中4个年龄段的人数各100人)食用轻食的频数与年龄得到如下的频数分布表.使用频数[)12,25[)25,38[)38,51[]51,64偶尔1次3015510每周1~3次40403050每周4~6次25404530每天1次及以上552010(1)若把年龄在[)12,38的消费者称为青少年,年龄在[]38,64的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成22⨯列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;(2)从每天食用轻食1次及以上的样本消费者中按照表中年龄段采用分层抽样,从中抽取8人,再从这8人中随机抽取3人,记这3人中年龄在[)25,38与[]51,64的人数分别为X ,Y ,X Y ξ=-.求ξ的分布列与期望;(3)已知小李每天早餐、晚餐都食用轻食,且早餐与晚餐在低卡甜品、全麦夹心吐司、果蔬汁3种轻食中选择一种,已知小李在某天早餐随机选择一种轻食,如果早餐选择低卡甜品、全麦夹心吐司、果蔬汁,则晚餐选择低卡甜品的概率分别为15,25,23,求小李晚餐选择低卡甜品的概率.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.附:()2P K k ≥0.100.050.010.0050.001k2.7063.8416.6357.87910.82819.如图,已知四棱台1111ABCD A B C D -的上、下底面分别是边长为2和4的正方形,14A A =,且1A A ⊥底面ABCD ,点P ,Q 分别在棱1DD 、BC 上.(1)若P 是1DD 的中点,证明:1AB PQ ⊥;(2)若//PQ 平面11ABB A ,二面角P QD A --的余弦值为49,求四面体ADPQ 的体积.20.已知圆C:22130x y ++-=,点P 是圆C上的动点,点)F是圆C 内一点,线段PF 的垂直平分线交CP 于点M ,当点P 在圆C 上运动时点M 的轨迹为E .(1)求E 的方程;(2)T 为直线l :4x =上的动点,A 、B 为曲线E 与x 轴的左右交点,TA 、TB 分别与曲线E 交于G 、D 两点.证明:GA DT GT DB⋅⋅为定值.21.()2cos 1f x x mx =+-(x ∈R ).(1)当12m ≥时,证明:()0f x ≥;(2)证明:11112111tan1212tan 3tan tan23n n n n n+++⋅⋅⋅+>-+.请考生在22,23二题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,直线l 的参数方程为cos 1sin x t y t αα=⋅⎧⎨=+⋅⎩(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为()21cos 0ρθθ⋅--=.(1)写出直线l 的普通方程及曲线C 的直角坐标方程;(2)已知点())0,1,P Q,直线l 过点Q 且与曲线C 相交于A 、B 两点,设线段AB的中点为M ,求PM 的值.[选修4-5:不等式选讲]23.已知关于x 的不等式2261x x m m +----≥有解.(1)求实数m 的取值范围.(2)若a 、b 、c 均为正数,n 为m 的最大值,且34a b c n ++=.求证:2221252a ab bc +++≥.德阳市高中2021级质量监测考试(二)数学试卷(理工农医类)说明:1.本试卷分第Ⅰ卷和第Ⅱ卷,共4页,考生作答时,须将答案答在答题卡上,在本试卷、草稿纸上答题无效.考试结束后,将答题卡交回,2.本试卷满分150分,120分钟完卷.第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.若1=+z ,则2zz =-()A.12B.1C.D.2【答案】B 【解析】【分析】运用复数的运算求出2zz -,再利用复数模的公式即可求解.【详解】由题,1113i 222z z +--==--,13=i 1222z z ∴-=-.故选:B.2.已知集合{}260A x x x =--≤,10ln B xx ⎧⎫=≥⎨⎬⎩⎭,则A B = ()A.{}12x x <≤B.{}12x x ≤≤C.{}13x x <≤ D.{}13x x ≤≤【答案】C 【解析】【分析】解不等式求得集合,A B ,进而求得A B ⋂.【详解】()()26230x x x x --=+-≤,解得23x -≤≤,所以{}|23A x x =-≤≤.由10ln x≥得ln 0x >,解得1x >,所以{}|1B x x =>.所以{}|13A B x x ⋂=<≤.故选:C3.若x ,y 满足约束条件2202201x y x y y +-≥⎧⎪--≤⎨⎪≤⎩,则43z x y =+的最大值为()A.19B.13C.9D.5【答案】A 【解析】【分析】画出可行域,结合图形计算可得.【详解】根据线性约束条件,画出可行域如下所示:目标函数43z x y =+可转化为433zy x =-+,因此,当直线433zy x =-+在y 上的截距最大时,目标函数43z x y =+取得最大值,由图象可得当直线433zy x =-+过点()4,1A 时,在y 上的截距最大,所以43z x y =+得最大值为max 443119z =⨯+⨯=.故选:A.4.已知()9,A m 为抛物线C :22y px =(0p >)上一点,点A 到C 的焦点的距离为12,则p =()A.2B.3C.6D.9【答案】C 【解析】【分析】根据抛物线的定义列方程来求得p 的值.【详解】根据抛物线的定义可知,912,62pp +==.故选:C5.质数(prime number )又称素数,一个大于1的自然数,除了1和它本身外,不能被其他自然数整除,则这个数为质数,数学上把相差为2的两个素数叫做“孪生素数”.如:3和5,5和7……,在1900年的国际数学大会上,著名数学家希尔伯特提出了23个问题,其中第8个就是大名鼎鼎的孪生素数猜想:即存在无穷多对孪生素数.我国著名数学家张益唐2013年在《数学年刊》上发表论文《素数间的有界距离》,破解了困扰数学界长达一个半世纪的难题,证明了孪生素数猜想的弱化形式.那么,如果我们在不超过30的自然数中,随机选取两个不同的数,记事件A ,这两个数都是素数;事件B :这两个数不是孪生素数,则()P B A =()A.1115B.3745C.1315D.4145【答案】D 【解析】【分析】根据条件概率的计算方法求得正确答案.【详解】不超过30的自然数有30个,其中素数有2,3,5,7,11,13,17,19,23,29共10个,孪生素数有3和5,5和7,11和13,17和29,共4组.所以()210230C 9C 87P A ==,()210230C 441C 435P AB -==,所以()()()41418741435943594587P AB P B A P A ===⨯=.故选:D6.一个球与正四面体的六条棱都相切,若正四面体的棱长为a ,则这个球的体积为()A.32π12a B.32π24a C.33π12a D.33π24a 【答案】B 【解析】【分析】将正四面体放置在正方体中,由正方体的内切球的体积来确定正确答案.【详解】如图所示,正四面体11A B CD -在正方体1111ABCD A B C D -中,一个球与正四面体11A B CD -的六条棱都相切,则该球与正方体1111ABCD A B C D -内切,正四面体的棱长为a,也即是球的直径222R a =,半径24R a =,所以体积为334π22ππ3224a a ⎛⎫⨯= ⎪ ⎪⎝⎭.故选:B7.已知各项不相等的等比数列{}n a 的前n 项和为n S ,若534S S -=,5678a a a =,则1a =()A.116-B.116C.64-D.64【答案】C 【解析】【分析】根据已知条件,以及等比数列的基本量运算求得1a .【详解】设等比数列{}n a 的公比为q ,0q ≠,依题意,345345451135567661444,,822S S a a a a a q a q a a a a a a q -=+=+=⎧+=⎧⎧⎨⎨⎨====⎩⎩⎩,两式相除得()()3425212,212110q q q q q q q q q++==--=+-=,解得12q =-或1q =(舍去),所以15264a q ==-.故选:C8.已知函数()f x 的定义域为R ,且满足()()cos 222xxf x x ϕ-=++-,则“sin 1ϕ=”是“()f x 是奇函数”的()A.充分不必要条件B.必要不充分条件C.充分必要条件D.既不充分也不必要条件【答案】A 【解析】【分析】根据函数的奇偶性、诱导公式、充分和必要条件等知识确定正确答案.【详解】依题意,()()cos 222xxf x x ϕ-=++-,①若sin 1ϕ=,则π2π,Z 2k k ϕ=+∈,所以()πcos 22π22222sin 2x x x x f x x k x --⎛⎫=+++-+- ⎪-⎭=⎝,此时()()sin 222xx f x x f x --=+-=-,()f x 是奇函数.②若()f x 是奇函数,则由于()f x 的定义域是R ,所以()π0cos 0,π2f k ϕϕ===+,此时()()sin 2πcos 2π22π222x x x xf x x x k k --⎛⎫=+++-+- =-⎝+⎪⎭为奇函数,符合题意,所以πsin sin πcos π12k k ϕ⎛⎫=+==± ⎪⎝⎭.所以“sin 1ϕ=”是“()f x 是奇函数”的充分不必要条件.故选:A9.已知平面向量a ,b ,c 满足1a b == ,2c = ,若b ,c共线,且a b c ++= ,则a b c +-=()A.B.C.D.【答案】B 【解析】【分析】由b 与c共线,分共线同向和共线反向讨论,并结合向量模和数量积运算求解.【详解】因为b 与c共线,1a b == ,2c = ,当b 与c共线同向时,则2c b =r r,所以3a b c a b ++=+r r r r u u r,332a b c a b a b ∴++=+≥-=r r r r u u r r u u r,这与a b c ++=矛盾,所以b 与c 共线反向时,则2c b =- ,a b c a b ∴++=-=r r r r r,23a b ∴-=r r ,即2223a b a b +-⋅=r r r r ,解得12a b ⋅=- ,3a b c a b ∴+-=+=r r r r r故选:B.10.已知双曲线C :22221x y a b -=(0a >,0b >),O 为坐标原点,F 为C 的右焦点,以F为圆心,OF 为半径的圆与C 的渐近线在第一象限的交点为A ,若OAF △的面积为22a ,则双曲线的离心率为()A.2B.C.72D.2【答案】A 【解析】【分析】根据三角形OAF 的面积列方程,求得,a b 的关系式,进而求得双曲线的离心率.【详解】双曲线的渐近线OA 的方程为by x a =,设其倾斜角为θ,θ为锐角,且tan b aθ=,由于FO FA c ==,所以()22211sin π2sin 2222OAFa S c θθ=-==,2222222222sin cos 2tan 2sin cos tan 11bab a a b c c a θθθθθθ====+++,所以12b a =,所以52ce a=====.故选:A11.若函数()13f x x m x x=++-在[)2,+∞上单调递增,则实数m 的取值范围是()A.3,4⎛⎤-∞ ⎥⎝⎦B.8,9∞⎛⎤- ⎥⎝⎦C.38,49⎡⎤⎢⎥⎣⎦ D.83,94⎡⎤-⎢⎥⎣⎦【答案】D 【解析】【分析】化简函数()()()113,3113,23m x m x xf x m x m x x ⎧++-≥⎪⎪=⎨⎪-++≤<⎪⎩,分类讨论,结合()0f x '≥恒成立,即可求解.【详解】由函数()()()113,313113,23m x m x xf x x m x x m x m x x ⎧++-≥⎪⎪=++-=⎨⎪-++≤<⎪⎩,当3x ≥时,()()113f x m x m x =++-,可得()211f x m x'=+-,要使得()f x 在[3,)+∞为单调递增函数,则()0f x '≥恒成立,即2110m x +-≥在[3,)+∞恒成立,即211m x ≥-在[3,)+∞恒成立,可得89m ≥-;当23x ≤<时,()()113f x m x m x =-++,可得()211f x m x'=--,要使得()f x 在[2,3)为单调递增函数,则()0f x '≥恒成立,即2110m x --≥在[2,3)恒成立,即211m x ≤+在[2,3)恒成立,可得34m ≤,综上可得,实数m 的取值范围83,94⎡⎤-⎢⎥⎣⎦.故选:D.12.已知三棱锥-P ABC 的三条侧棱PA 、PB 、PC 两两互相垂直,O 是ABC 的垂心.若1OBC S =△,4ABC S = ,则PBC S =△()A.85B.2C.52D.【答案】B【解析】【分析】先证明两个线面垂直“BC ⊥平面APE ”和“PO ⊥平面ABC ”,进而得到90APE POE ∠=∠=︒,得到等式2PE OE AE =⋅,并将其转化为关系式2()PBC S =△OBC ABC S S ⨯ △,求解即可.【详解】连接AO ,并延长AO 交BC 于点E ,连接PE ,连接,,OB OC OP ,由于三条侧棱PA 、PB 、PC 两两互相垂直,易得AP ⊥平面PBC ,又因为PE ⊂平面PBC ,BC ⊂平面PBC ,所以AP PE ⊥,⊥AP BC ,因为O 是ABC 的垂心,所以AE BC ⊥,因为AE BC ⊥,⊥AP BC ,且AE ⊂平面APE ,AP ⊂平面APE ,AE AP A =I ,所以BC ⊥平面APE ,且PO ⊂平面APE ,所以BC PO ⊥,同理可得AC PO ⊥,因为BC PO ⊥,AC PO ⊥,且BC ⊂平面ABC ,AC ⊂平面ABC ,BC AC C ⋂=,所以PO ⊥平面ABC ,AE ⊂平面ABC ,所以PO AE ⊥,因为90,APE POE PEO AEP ∠=∠=︒∠=∠,所以APE POE ,PE OEAE PE=,即2PE OE AE =⋅,所以2111()()()222PE BC OE BC AE BC ⨯=⨯⋅⨯,由BC ⊥平面APE ,易得,BC PE BC AE ⊥⊥,所以2()PBC S =△144OBC ABC S S ⨯=⨯= △,所以2PBC S = .故选:B.第Ⅱ卷(非选择题共90分)本卷包括必考题和选考题两部分,第13~21题为必考题,每个试题考生都必须作答,第22、23题为选考题,考生根据要求作答.二、填空题:共4小题,每小题5分,共20分.将答案填在答题卡上.13.在()()6311x x -+的展开式中,3x 的系数为______.【答案】25【解析】【分析】分别求解展开式()61x +中含2x ,3x 的项,再求出展开式()()6311x x -+中含3x 的项的系数即可.【详解】()61x +的展开式中2x 项为426C x ,3x 的项为363C x ,所以()()6311x x -+中含3x 的项的系数为43663C C 25-=.故答案为:25.14.已知数列{}n a 满足11a =,且对任意*n ∈N ,有()11nn n a a n +=+-⋅,则22a =______.【答案】10-【解析】【分析】利用累加法求得22a .【详解】依题意,211a a =-,322a a =+,433=-a a ,544a a =+,……212020a a =+,222121a a =-,上述21个式子相加得2211012111110a a =+⨯-=-=-.故答案为:10-15.已知函数()ln ln f x a x bx =⋅-在1x =处取得极大值,则ba的取值范围是______.【答案】10,e⎛⎤ ⎥⎝⎦【解析】【分析】由()10f '=以及导数、极大值等知识对问题进行分析,利用构造函数法,结合导数来求得ba的取值范围.【详解】()f x 的定义域是()0,∞+,()ln ln a bx af x b x x-+'=-=,由于函数()ln ln f x a x bx =⋅-在1x =处取得极大值,所以()1ln 0,ln ,e bf b a a b a '=-+===,且()f x 在()0,1上()()0,f x f x '>单调递增,在()1,+∞上()()0,f x f x '<单调递减,所以ln y bx a =-+单调递减,所以0,0b b -<>,所以()0e b b bb a =>,构造函数()()0e x x g x x =>,显然()0g x >,()1ex xg x ='-,所以()g x 在区间()0,1上()()0,g x g x '>单调递增,在区间()1,+∞上()()0,g x g x '<单调递减,所以()11e g =是()g x 的极大值也即是最大值,所以()10,e g x ⎛⎤∈ ⎥⎝⎦,也即ba 的取值范围是10,e ⎛⎤ ⎥⎝⎦.故答案为:10,e⎛⎤ ⎥⎝⎦16.已知正实数x ,y ,z 满足26x xy yz xz x z +++++=,则32x y z ++的最小值是______.【答案】2-【解析】【分析】因式分解得到61x z x y +=++,变形后得到()13622x z y x y x y +=+++++,利用基本不等式求出最小值.【详解】因为,,x y z 为正实数,故()()()2266xxy yz xz x z x xzxyyz x z +⇒,即()()()()()66161x x z y x z x z x y x z x z x y ++++=⇒+++=⇒+=+++,()()()132622x y z x y x x y y z x ++=+++++++=()6222121x y x y =-≥-=+++++,当且仅当()1261y y x x ++++=,即1x y +=-,此时61x z x y +==++,所以32x y z ++的最小值为2-.故答案为:2-三、解答题:解答应写出文字说明、证明过程或演算步骤.17.在ABC 中,角A 、B 、C 所对的边分别为a 、b 、c ,且sin cos 32c BC =,3b =.(1)求B ;(2)若ABC 为锐角三角形,求ABC 的面积范围.【答案】(1)π3(2)3393(,]24【解析】【分析】(1)根据sin cos 32c BC =,3b =,利用正弦定理得到sin sin sin cos 2B BC C =,再利用三角恒等变换求解;(2)设ABC 的外接圆半径为R ,得到2sin bR B==1sin 2ABC S ac B =△33π33sin 2264A ⎛⎫=-+ ⎪⎝⎭求解.【小问1详解】因为sin cos 32c BC =,3b =,所以sin sin sin cos 2BB C C =,因为sin 0C ≠,所以sin cos 2B B =,则2sin cos cos 222B B B =,因为cos02B≠,所以1sin 22B =,又π0,22B ⎛⎫∈ ⎪⎝⎭,则π26B =,所以π3B =.【小问2详解】设ABC 的外接圆半径为R ,则2sin bR B==所以112πsin 2sin 2sin sin sin 223ABC S ac B R A R C B A A ⎛⎫===- ⎪⎝⎭,1cos sin22A A A⎛⎫=+⎪⎪⎝⎭,2991cos2sin cos sin sin222422AA A A A-=+=+⋅,93333sin2cos2444A A=-+,πsin2264A⎛⎫=-+⎪⎝⎭,因为ABC为锐角三角形,所以π22ππ32AA⎧<<⎪⎪⎨⎪<-<⎪⎩,解得ππ62A<<,则ππ5π2666A<-<,则1πsin2126A⎛⎫<-≤⎪⎝⎭,所以339324ABCS<≤,所以ABC的面积范围(24.18.轻食是餐饮的一种形态、轻的不仅仅是食材分量,更是食材烹饪方式简约,保留食材本来的营养和味道,近年来随着消费者健康意识的提升及美颜经济的火热,轻食行业迎来快速发展.某传媒公司为了获得轻食行业消费者行为数据,对中国轻食消费者进行抽样调查.统计其中400名中国轻食消费者(表中4个年龄段的人数各100人)食用轻食的频数与年龄得到如下的频数分布表.使用频数[)12,25[)25,38[)38,51[]51,64偶尔1次3015510每周1~3次40403050每周4~6次25404530每天1次及以上552010(1)若把年龄在[)12,38的消费者称为青少年,年龄在[]38,64的消费者称为中老年,每周食用轻食的频数不超过3次的称为食用轻食频率低,不低于4次的称为食用轻食频率高,根据所给数据,完成22⨯列联表,并根据列联表判断是否有99%的把握认为食用轻食频率的高低与年龄有关;(2)从每天食用轻食1次及以上的样本消费者中按照表中年龄段采用分层抽样,从中抽取8人,再从这8人中随机抽取3人,记这3人中年龄在[)25,38与[]51,64的人数分别为X ,Y ,X Y ξ=-.求ξ的分布列与期望;(3)已知小李每天早餐、晚餐都食用轻食,且早餐与晚餐在低卡甜品、全麦夹心吐司、果蔬汁3种轻食中选择一种,已知小李在某天早餐随机选择一种轻食,如果早餐选择低卡甜品、全麦夹心吐司、果蔬汁,则晚餐选择低卡甜品的概率分别为15,25,23,求小李晚餐选择低卡甜品的概率.参考公式:()()()()()22n ad bc K a b c d a c b d -=++++,n a b c d =+++.附:()2P K k ≥0.100.050.010.0050.001k2.7063.8416.6357.87910.828【答案】(1)列联表见解析,有99%的把握认为食用轻食频率的高低与年龄有关,理由见解析(2)分布列见解析,数学期望为4156(3)1945【解析】【分析】(1)数据分析,得到列联表,计算出卡方,与6.635比较后得到结论;(2)先利用分层抽样得到[)12,25,[)25,38,[)38,51和[]51,64的抽取人数,得到X Y ξ=-的可能取值和对应的概率,得到分布列和数学期望;(3)设出事件,结合全概率公式得到答案.【小问1详解】列联表如下:青少年中老年合计食用轻食频率低12595220食用轻食频率高75105180合计200200400故()()()()()()22240012510595759.091 6.635220180200200n ad bc K a b c d a c b d -⨯⨯-⨯==≈>++++⨯⨯⨯,故有99%的把握认为食用轻食频率的高低与年龄有关;【小问2详解】每天食用轻食1次及以上的样本消费者中按照表中年龄段采用分层抽样,[)12,25的抽取人数为581552010⨯=+++,[)25,38的抽取人数为581552010⨯=+++,[)38,51的抽取人数为2084552010⨯=+++,[]51,64的抽取人数为1082552010⨯=+++,X 的可能取值为0,1,此时Y 的取值为0,1,2,故X Y ξ=-的可能取值为0,1,2,其中0ξ=包含两种情况,即0X Y ==和1X Y ==,故()311151253388C C C C 50C C 14P ξ==+=,1ξ=包含三种情况,0,1X Y ==,1,0X Y ==和1,2X Y ==,故()012102120125125125333888C C C C C C C C C 311C C C 56P ξ==++=,2ξ=包含1种情况,即0,2X Y ==,故()02112538C C C 52C 56P ξ===,故ξ的分布列如下:ξ012P5143156556则数学期望为()53154101214565656E ξ=⨯+⨯+⨯=;【小问3详解】记小李早餐选择低卡甜品、全麦夹心吐司、果蔬汁,分别为事件,,A B C ,则()13P A =,()13P B =,()13P C =,小李晚餐选择低卡甜品为事件D ,则()15P D A =,()25P D B =,()23P D C =,故()()()()()()()1112121935353345P D P A P D A P B P D B P C P D C =++=⨯+⨯+⨯=,故小李晚餐选择低卡甜品的概率为1945.19.如图,已知四棱台1111ABCD A B C D -的上、下底面分别是边长为2和4的正方形,14A A =,且1A A ⊥底面ABCD ,点P ,Q 分别在棱1DD 、BC 上.(1)若P 是1DD 的中点,证明:1AB PQ ⊥;(2)若//PQ 平面11ABB A ,二面角P QD A --的余弦值为49,求四面体ADPQ 的体积.【答案】(1)证明见解析(2)83【解析】【分析】(1)建立空间直角坐标系,利用向量法证明异面直线的垂直;(2)求平面法向量,由二面角P QD A --的余弦值为49和//PQ 平面11ABB A ,解得P 点坐标,可求四面体ADPQ 的体积.【小问1详解】以A 为坐标原点,AB ,AD ,1AA 所在直线分别为x ,y ,x轴建立空间直角坐标系,则()0,0,0A ,()12,0,4B ,()0,4,0D ,()10,2,4D ,设()4,,0Q m ,其中m BQ =,04m ≤≤,若P 是1DD 的中点,则()0,3,2P ,()12,0,4AB = ,()4,3,2PQ m =--,于是1880AB PQ ⋅=-= ,∴1AB PQ ⊥,即1AB PQ ⊥.【小问2详解】由题设知,()4,4,0DQ m =- ,()10,2,4DD =-是平面PDQ 内的两个不共线向量.设()1,,n x y z =是平面PDQ 的一个法向量,则()111440,240,n DQ x m y n DD y z ⎧⋅=+-=⎪⎨⋅=-+=⎪⎩ 取4y =,得()14,4,2n m =- .又平面AQD 的一个法向量是()20,0,1n =,∴121212cos ,n nn n n n ⋅==⋅,而二面角P QD A --的余弦值为4949=,解得72m =或92m =(舍去),此时74,,02Q ⎛⎫⎪⎝⎭.设1DP DD λ=(01λ<≤),而()10,2,4DD =- ,由此得点()0,42,4P λλ-,14,2,42PQ λλ⎛⎫=-- ⎪⎝⎭,∵//PQ 平面11ABB A ,且平面11ABB A 的一个法向量是()30,1,0n =,∴30PQ n ⋅= ,即1202λ-=,解得14λ=,从而70,,12P ⎛⎫ ⎪⎝⎭.将四面体ADPQ 视为以ADQ △为底面的三棱锥P ADQ -,则其高1h =,故四面体ADPQ 的体积11184413323ADQ V S h =⋅=⨯⨯⨯⨯= .20.已知圆C:22130x y ++-=,点P 是圆C上的动点,点)F是圆C 内一点,线段PF 的垂直平分线交CP 于点M ,当点P 在圆C 上运动时点M 的轨迹为E .(1)求E 的方程;(2)T 为直线l :4x =上的动点,A 、B 为曲线E 与x 轴的左右交点,TA 、TB 分别与曲线E 交于G 、D 两点.证明:GA DT GT DB⋅⋅为定值.【答案】(1)2214x y +=(2)证明过程见解析【解析】【分析】(1)根据线段垂直平分线的性质,结合椭圆的定义进行求解即可;(2)设出相应直线方程与椭圆方程联立,利用一元二次方程根与系数关系,结合两点间距离公式进行求解即可.【小问1详解】如图所示:连接MF ,由(222213016x y x y++-=⇒++=,所以该圆的圆心坐标为()C ,半径为4,因为线段PF 的垂直平分线交CP 于点M ,所以有MP MF =,由44MC MP PC MC MF CF +==⇒+=>,所以点M 的轨迹是以,C F 为焦点的椭圆,即24,22,1a c a c b =====,所以E 的方程为2214x y +=;【小问2详解】设()4,T m ,()()2,0,2,0A B -,因为直线TA 的斜率为6m ,所以直线TA 的方程为()26my x =+,代入椭圆方程中,得()2222944360m xm x m +++-=,显然有2222436182299G G m m x x m m ---=⇒=++,22218262699G m m m y m m ⎛⎫-=+= ⎪++⎝⎭,即2221826,99m m G m m ⎛⎫- ⎪++⎝⎭,因为直线TB 的斜率为2m ,所以直线TB 的方程为()22my x =-,代入椭圆方程中,得()222214440m xm x m +-+-=,显然有22224422211D D m m x x m m --=⇒=++,2222222211D m m m y m m ⎛⎫--=-= ⎪++⎝⎭,即222222,11m m D m m ⎛⎫-- ⎪++⎝⎭,于是有29GA m ==+,(2239m GT m +==+,(2231m DT m +==+,2241DB m ==+,因此(2222236369132491m GA DT m m GT DB m m +⨯⋅==⋅++为常数.【点睛】关键点睛:本题的关键是利用一元二次方程根与系数的关系求出相关点的坐标.21.()2cos 1f x x mx =+-(x ∈R ).(1)当12m ≥时,证明:()0f x ≥;(2)证明:11112111tan1212tan 3tan tan23n n n n n+++⋅⋅⋅+>-+.【答案】(1)证明过程见解析(2)证明过程见解析【解析】【分析】(1)放缩得到()221cos 1cos 12f x x mx x x =+≥+--,构造()21cos 12g x x x =+-,得到函数的奇偶性,二次求导,得到函数的单调性,结合特殊点的函数值,证明出结论;(2)由(1)知21cos 12x x ≥-,令1x n =,1n ≥且n N *∈放缩得到21211cos 11412121n n n n ⎛⎫>-=-- ⎪--+⎝⎭,再由sin x x ≥得到11cos 1tan n n n >,从而得到111112121tan n n n n⎛⎫>-- ⎪-+⎝⎭,相加后得到结论.【小问1详解】当12m ≥时,()221cos 1cos 12f x x mx x x =+≥+--,令()21cos 12g x x x =+-,()()()()2211cos 1cos 122g x x x g x x x -=-++--==-,故()21cos 12g x x x =+-为偶函数,()sin g x x x '=-+,令()()sin h x g x x x '==-+,()()()()sin sin h x x x x x h x +-=---=-=-,故()()sin h x g x x x '==-+为奇函数,其中()1cos 0h x x '=-≥恒成立,故()()sin h x g x x x '==-+在[)0,∞+上单调递增,其中()00h =,故()0h x ≥在[)0,∞+恒成立,故()21cos 12g x x x =+-在[)0,∞+上单调递增,其中()cos00100g +=-=,故()0g x ≥在[)0,∞+上恒成立,结合()21cos 12g x x x =+-为偶函数,故()0g x ≥在R 上恒成立,故()2cos 10f x x mx =+-≥在R 上恒成立;【小问2详解】由(1)知,21cos 102x x +-≥,即21cos 12x x ≥-,当且仅当0x =时,等号成立,令1x n =,1n ≥且n N *∈,所以101n <≤,故211cos 12n n>-,即222112211cos111124412121n n n n n n ⎛⎫>-=->-=-- ⎪--+⎝⎭,由(1)可知,当0x ≥时,sin x x ≥,当且仅当0x =时,等号成立,当1n ≥且n N *∈时,101n<≤,故1111sin cos tan n n n n >=,故11cos 1tan n n n>,即11cos 1tan n n n >,所以1111cos112121tann n n n n⎛⎫>>-- ⎪-+⎝⎭,故11111111111111tan133521212tan tan2n n n n ⎛⎫⎛⎫⎛⎫+++>--+--++-- ⎪ ⎪ ⎪-+⎝⎭⎝⎭⎝⎭ 1111121335212121n n n n n n ⎛⎫=--+-++-=- ⎪-++⎝⎭.【点睛】方法点睛:导函数证明数列相关不等式,常根据已知函数不等式,用关于正整数的不等式代替函数不等式中的自变量,通过多次求和(常常用到裂项相消法求和)达到证明的目的,此类问题一般至少有两问,已知的不等式常由第一问根据特征式的特征而得到.请考生在22,23二题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做第一个题目计分,做答时,请用2B 铅笔在答题卡上将所选题号后的方框涂黑.[选修4-4:坐标系与参数方程]22.在直角坐标系xOy 中,直线l 的参数方程为cos 1sin x t y t αα=⋅⎧⎨=+⋅⎩(t 为参数).以坐标原点为极点,x 轴的正半轴为极轴建立极坐标系,已知曲线C 的极坐标方程为()21cos 0ρθθ⋅--=.(1)写出直线l 的普通方程及曲线C 的直角坐标方程;(2)已知点())0,1,P Q,直线l 过点Q 且与曲线C 相交于A 、B 两点,设线段AB的中点为M ,求PM 的值.【答案】(1)sin cos cos 0x y ααα-+=;2y =.(2)8【解析】【分析】(1)根据已知方程即可求出直线l 的普通方程及曲线C 的直角坐标方程;(2)求出直线l 的倾斜角,将l 的参数方程代入曲线C 的极坐标方程并化简,结合韦达定理即可求出PM 的值.【小问1详解】由题意,在cos :1sin x t l y t αα=⋅⎧⎨=+⋅⎩(t 为参数)中,cos 1sin x y αα=-,即:sin cos cos 0x y ααα-+=,在()21cos0ρθθ⋅--=中,()221cos cos 0ρθθ⋅--=,∵22sin cos 1,cos ,sin x y θθρθρθ+===∴()222221coscos sin cos 0y ρθθρθθ⋅--=⋅--==,∴曲线C的直角坐标方程为:2y =【小问2详解】由题意,())0,1,P Q,在:sin cos cos 0l x y ααα-+=中,直线l 过点Q ,cos 0αα+=,解得:3tan 3α=-,∴1sin ,cos 22αα==-,32:112x t l y t⎧=-⎪⎪⎨⎪=+⎪⎩,将l 的参数方程代入曲线C 的极坐标方程,并化简得21640t t ++=,∴1216t t +=-设点,,A B M 对应的参数为120,,t t t ,∴12016822t t P t M +-====.[选修4-5:不等式选讲]23.已知关于x 的不等式2261x x m m +----≥有解.(1)求实数m 的取值范围.(2)若a 、b 、c 均为正数,n 为m 的最大值,且34a b c n ++=.求证:2221252a ab bc +++≥.【答案】(1)(,3]-∞(2)证明见解析【解析】【分析】(1)根据题意,由绝对值不等式可得()max2265x x +--=,再将不等式有解转化为51m m ≥+-,即可得到结果;(2)根据题意,由(1)可知3n =,再由柯西不等式代入计算,即可证明.【小问1详解】由题意可得,2261x x m m +----≥,即2261x x m m+--≥+-令8,2()22634,238,3x x f x x x x x x x -≤-⎧⎪=+--=--<<⎨⎪-+≥⎩,当(],2x ∞∈--时,()(],10f x ∞∈--,当()2,3x ∈-时,()()10,5f x ∈-,当[)3,x ∞∈+,()(],5f x ∞∈-所以()f x 的最大值为5,关于x 的不等式2261x x m m +--≥+-有解等价于()max 51f x m m =≥+-,当m 1≥时,不等式转化为51m m ≥+-,即521m ≥-,解得3m ≤,所以13m ≤≤,当1m <时,不等式转化为51m m ≥+-,即51≥,解集R ,所以1m <,综上所述,实数m 的取值范围为(,3]-∞.【小问2详解】由(1)可知,m 的取值范围为(3],-∞,且n 为m 的最大值,所以3n =,则343a b c ++=,即243a b b c +++=,由柯西不等式可得()()()()22222222114249a b b c a b b c ⎡⎤+++++≥+++=⎣⎦,当且仅当2114a b b c +==时,即12123,a b c ===时,等号成立,又()222222254a ab b c a b b c +++=+++,所以()22218259a ab b c +++≥,即2221252a ab bc +++≥.【点睛】方法点睛:绝对值不等式的解法,法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想;法二:利用“零点分段法”求解,体现了分类讨论的思想;法三:通过构造函数,利用函数的图象求解,体现了函数与方程的思想.。
四川省德阳市2014-2015学年高二下学期期末数学试卷(文科)一、选择题(本大题共10个小题,每小题5分,满分50分,在每小题给出的四个选项中,只有一个项是符合题目要求的。
)1.复数(i为虚数单位)的共轭复数为( )A.1+i B.1﹣i C.﹣1+i D.﹣1﹣i考点:复数代数形式的乘除运算.专题:计算题.分析:复数分母实数化,然后求出复数的共轭复数即可.解答:解:==1+i.∴所求复数的共轭复数为:1﹣i.故选:B.点评:本题考查复数的基本运算,复数的基本概念,考查计算能力.2.已知集合P={x|y=lg(2﹣x)},Q={x|x2﹣5x+4≤0},则P∩Q=( )A.{x|1≤x<2} B.{x|1<x<2} C.{x|0<x<4} D.{x|0≤x≤4}考点:一元二次不等式的解法;对数函数的定义域.专题:集合.分析:先求出集合P与集合Q,再进行交集运算即可.解答:解:∵2﹣x>0,∴x<2.∴P={x|x<2},解x2﹣5x+4≤0,得﹣4≤x≤﹣1,则Q={x|1≤x≤4},∴P∩Q={x|1≤x<2}.故选:A.点评:本题考查交集及其运算以及对数函数的定义域和不等式的解法,正确化简集合P和Q 是解题的关键.3.执行如图所示的程序框图,若输入如下四个函数:①f(x)=sinx②f(x)=cosx③f(x)=④f(x)=log2x则输出的函数是( )A.f(x)=sinx B.f(x)=cosx C.f(x)=D.f(x)=log2x考点:余弦函数的奇偶性.专题:三角函数的图像与性质.分析:由程序框图可得,本题输出的结果是存在零点的奇函数,再利用所给函数的奇偶性、零点,从而得出结论.解答:解:由程序框图可得,本题输出的结果是存在零点的奇函数,二所给的4个函数中,只有f(x)=sinx是存在零点的奇函数,其余的三个函数都不满足此条件,②f(x)=cosx是偶函数;③f(x)=是奇函数但它没有零点;④f(x)=log2x是非奇非偶函数,故选:A.点评:本题主要考查程序框图,三角函数的奇偶性、函数的零点的定义,术语基础题.4.将长方体截去一个四棱锥,得到的几何体如图所示,则该几何体的左视图( )A.B.C.D.考点:简单空间图形的三视图.专题:作图题;压轴题.分析:根据三视图的特点,知道左视图从图形的左边向右边看,看到一个正方形的面,在面上有一条对角线,对角线是由左下角到右上角的线,得到结果.解答:解:左视图从图形的左边向右边看,看到一个正方形的面,在面上有一条对角线,对角线是由左下角到右上角的线,故选D.点评:本题考查空间图形的三视图,考查左视图的做法,本题是一个基础题,考查的内容比较简单,可能出现的错误是对角线的方向可能出错.5.以(2,﹣1)为圆心且与直线3x﹣4y+5=0相交所得弦长为8的圆的标准方程为( ) A.(x﹣2)2+(y+1)2=9 B.(x+2)2+(y﹣1)2=9 C.(x﹣2)2+(y+1)2=25 D.(x+2)2+(y﹣1)2=25考点:直线与圆相交的性质.专题:直线与圆.分析:设圆的半径为r,由题意可得弦心距d==,求得r的值,可得圆的标准方程.解答:解:设圆的半径为r,由于(2,﹣1)为圆心,弦长为8,可得弦心距d==,求得 r=5,可得圆的标准方程为(x﹣2)2+(y+1)2=25,故选:C.点评:本题主要考查直线和圆相交的性质,点到直线的距离公式,弦长公式的应用,术语中档题.6.已知a是实数,则<1是a>1的( )A.既不充分又不必要条件B.充要条件C.充分不必要条件D.必要不充分条件考点:充要条件.专题:简易逻辑.分析:解出关于a的不等式,结合充分必要条件的定义,从而求出答案.解答:解:解不等式<1得:a<0或a>1,故<1是a>1的必要不充分条件,故选:D.点评:本题考查了充分必要条件,考查解不等式问题,是一道基础题.7.将函数f (x)=sin2x (x∈R)的图象向右平移个单位,则所得到的图象对应的函数的一个单调递增区间是( )A.(﹣,0)B.(0,)C.(,)D.(,π)考点:函数y=Asin(ωx+φ)的图象变换;复合三角函数的单调性.专题:计算题.分析:将函数f (x)=sin2x (x∈R)的图象向右平移个单位,可得到g(x)=f (x﹣)=sin2(x﹣)=﹣cos2x (x∈R),求得其单调递增区间,再判断即可.解答:解:f (x)=sin2x (x∈R)g(x)=f (x﹣)=sin2(x ﹣)=﹣cos2x=cos(2x+π )(x∈R),∵g(x)=cos(2x+π )的单调递增区间由2kπ﹣π≤2x+π≤2kπ得:kπ﹣π≤x≤kπ﹣(k∈Z).∴当k=1时,0≤x≤.而(0,)⊆[0,],故选B.点评:本题考查函数y=Asin(ωx+φ)的图象变换,关键在于掌握图象变换的规则(方向与单位),属于中档题.8.设b、c、m是空间色三条不同直线,α、β、γ是空间的三个不同平面,在下面给出的四个命题中,正确的命题是( )A.若b⊥m,c⊥m,则b∥c B.m∥a,α⊥β,则m⊥βC.若b⊥α,c∥α,则b⊥c D.若β⊥α,γ⊥β,则γ∥α考点:四种命题.专题:空间位置关系与距离.分析:①若b⊥m,c⊥m,则b∥c,由线线平行的条件判断;②若m∥α,α⊥β,则m⊥β,由线面垂直的条件判断;③若b⊥α,c∥α,则b⊥c,由线面垂直的条件判断;④若β⊥α,γ⊥β,则γ∥α,由面面垂直的条件判断;解答:解:①若b⊥m,c⊥m,则b∥c,此命题不正确,因为垂直于同一条直线的两条直线可能相交,平行异面;②若m∥α,α⊥β,则m⊥β,此命题不正确,在此条件下,m∥β也是可以的;③若b⊥α,c∥α,则b⊥c,此命题正确,因为垂直于同一平面的两条直线一定平行;④若β⊥α,γ⊥β,则γ∥α,此命题不正确,可能平行也可能相交;故选:C.点评:本题考查空间中直线与平面之间的位置关系,解题的关键是有着较好的空间想像能力,以及对每个命题涉及的定理定义等熟练掌握并能灵活运用它们解题.9.直线4kx﹣4y﹣k=0与抛物线y2=x交于A,B两点,若|AB|=4,则弦AB的中点到直线x=﹣的距离等于( )A.B.C.2 D.4考点:直线与圆锥曲线的关系.专题:直线与圆;圆锥曲线的定义、性质与方程.分析:根据抛物线的方程求得抛物线的焦点坐标与准线方程,确定直线AB为过焦点的直线,根据抛物线的定义求得AB的中点到准线的距离,即可求得结论.解答:解:直线4kx﹣4y﹣k=0可化为k(4x﹣1)﹣4y=0,故可知直线恒过定点(,0)∵抛物线y2=x的焦点坐标为(,0),准线方程为x=﹣,∴直线AB为过焦点的直线,∴AB的中点到准线的距离==2,∴弦AB的中点到直线x=﹣的距离等于2+=.故选B.点评:本题主要考查了抛物线的简单性质.涉及抛物线的焦点弦的问题常需用抛物线的定义来解决.10.已知两个实数a、b(a≠b)满足ae a=be b,命题p:lna+a=lnb+b;命题q:(a+1)(b+1)<0.则下面命题是真命题的是( )A.p∨(¬q)B.p∧(¬q)C.p∨q D.p∧q考点:复合命题的真假.专题:简易逻辑.分析:由已知ae a=be b可联想构造函数y=xe x,求导后由函数的单调性结合x<﹣1时y恒小于0可得a,b均小于0而且一个比﹣1大一个比﹣1小,由此可以得到选项.解答:解:构造函数y=xe x,则y′=e x+xe x=(x+1)e x,∵e x>0,∴当x<﹣1时,y′<0,函数y=xe x为减函数,当x>﹣1时,y′>0,函数y=xe x为增函数,要使ae a=be b,则a,b必须均小于0而且一个比﹣1大一个比﹣1小,∴命题p为假命题,命题q为真命题.故选:C.点评:本题考查命题的真假判断与应用,训练了函数构造法,考查了利用导数研究函数的单调性,是中档题.二、填空题(共5小题,每小题5分,满分25分)11.用系统抽样法从160名学生中抽取容量为20的样本,将160名学生从1到160编号,按编号顺序平均分成20段(1~8号,9~16号,…,153~160号).若第16段应抽出的号码为125,则第1段中用简单随机抽样确定的号码是5.考点:系统抽样方法.专题:概率与统计.分析:由系统抽样的法则,可知第n组抽出个数的号码应为x+8(n﹣1),即可得出结论.解答:解:由题意,可知系统抽样的组数为20,间隔为8,设第一组抽出的号码为x,则由系统抽样的法则,可知第n组抽出个数的号码应为x+8(n﹣1),所以第16组应抽出的号码为x+8(16﹣1)=125,解得x=5.故答案为:5.点评:系统抽样形象地讲是等距抽样,系统抽样适用于总体中的个体数较多的情况,系统抽样属于等可能抽样.12.△ABC中,a=2,∠A=30°,∠C=45°,则△ABC的面积S的值是+1.考点:三角形的面积公式.专题:解三角形.分析:由正弦定理可得,求出c值,利用两角和正弦公式求出sinB的值,由S△ABC =acsinB 运算结果解答:解:B=180°﹣30°﹣45°=105°,由正弦定理可得,∴c=2.sinB=sin(60°+45°)==,则△ABC的面积S△ABC =acsinB=×2×2×=+1,故答案为:+1点评:本题考查两角和正弦公式,正弦定理的应用,求出sinB的值,是解题的关键.13.已知双曲线﹣=1(a>0,b>0)的一条渐近线方程是y=x,它的一个焦点在抛物线y2=24x的准线上,则双曲线的方程为.考点:抛物线的简单性质;双曲线的简单性质.专题:计算题;圆锥曲线的定义、性质与方程.分析:由抛物线标准方程易得其准线方程为x=﹣6,可得双曲线的左焦点为(﹣6,0),再根据焦点在x轴上的双曲线的渐近线方程渐近线方程是y=x,得a、b的另一个方程,求出a、b,即可得到双曲线的标准方程.解答:解:因为抛物线y2=24x的准线方程为x=﹣6,所以由题意知,点F(﹣6,0)是双曲线的左焦点,所以a2+b2=c2=36,①又双曲线的一条渐近线方程是y=x,所以a=b,②由①②解得a2=18,b2=18,所以双曲线的方程为.故答案为:.点评:本题主要考查双曲线和抛物线的标准方程与几何性质,考查学生的计算能力,属于基础题.14.在棱长都相等的四面体ABCD中,E、F分别是CD、BC的中点,则异面直线AE、DF所成角的余弦值是.考点:余弦定理的应用;异面直线及其所成的角.专题:解三角形;空间角.分析:画出四面体ABCD,并设BC=4,取CF的中点为M,则∠AEM或其补角便是异面直线AE、DF所成角,这时候可以求出CM,CE,ME,而由余弦定理可以求出AM,从而在△AEM中由余弦定理即可求出cos∠AEM,这便得到异面直线AE、DF所成角的余弦值.解答:解:如图,设BC=4,取CF中点M,连接AM,ME;∵E是CD中点;∴ME∥DF;∴∠AEM或其补角便是异面直线AE,DF所成角;则:,,,CE=2,CM=1;∴在△ACM中,由余弦定理得:AM2=CA2+CM2﹣2CA•CM•cos60°=16+1﹣4=13;∴在△AME中,由余弦定理得:cos∠AEM=;∴异面直线AE、DF所成角的余弦值是.故答案为:.点评:考查异面直线所成角的概念及其求法,清楚异面直线所成角的范围,等边三角形的中线也是高线,直角三角形边角的关系,以及余弦定理的应用.15.下列命题中正确的序号是②③①平面向量与的夹角为60°,=(2,0),||=1,则在上的投影为.②有一底面积半径为1,高为2的圆柱,点O为这个圆柱底面的圆心,在这个圆柱内随机抽取一点P,则点P到O点的距离大于1的概率为.③命题:“∀x∈(0,+∞),不等式cosx>1﹣x2恒成立”是真命题.④在约束条件下,目标函数z=ax+by(a>0,b>0)的最大值为6,则的最大值等于.考点:命题的真假判断与应用.专题:综合题.分析:①根据投影公式代入求出即可判断;②根据球和圆柱的体积公式求出即可;③构造函数,求出函数的导数,得到函数的单调性,从而得到结论;④画出平面区域,结合基本不等式的性质从而求出代数式的最大值.解答:解:①则在上的投影为:||cos60°=2×=1,故①错误;②∵到点O的距离等于1的点构成一个球面,如图,,则点P到点O的距离大于1的概率为:P====,故②正确;③构造函数h(x)=cosx﹣1+x2,h′(x)=﹣sinx+x,h″(x)=﹣cosx+1≥0,∴h′(x)在(0,+∞)上单调增∴h′(x)>h′(0)=0,∴函数h(x)在(0,+∞)上单调增,∴h(x)>0,∴cosx>1﹣x2,即不等式恒成立,故③正确;④:约束条件对应的平面区域如图3个顶点是(1,0),(1,2),(﹣1,2),由图易得目标函数在(1,2)取最大值6,此时a+2b=6,∵a>0,b>0,∴由不等式知识可得:a+2b=6≥2,∴ab≤,当且仅当:a=2b即:a=3,b=时“=”成立,要求的最大值转化为求的最小值即可,而=+≥2=2≥2=,∴的最大值等于,故④错误,故答案为:②③.点评:本题考查了向量的运算,考查概率问题,考查函数恒成立问题,基本不等式性质的应用以及线性规划问题,是一道综合题.三、解答题(本大题共6小题,满分75分解答应写出文字说明及演算步骤。
德阳市高中2015级“二诊”考试数学试卷(文史类)第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1. 已知为虚数单位,实数,满足,则()A. 1B.C.D.【答案】D【解析】,则故选D.2. 已知集合,集合,若,则()A. B. C. D.【答案】A【解析】得到,故选A.3. 函数的图象向右平移个单位后所得的图象关于原点对称,则可以是()A. B. C. D.【答案】B【解析】由题函数的图象向右平移个单位后所得的图象关于原点对称,即平移后得到的函数为奇函数,即为奇函数,对照选项可知选B.4. 实验测得四组数对的值为,,,,则与之间的回归直线方程是()参考公式:,.A. B.C. D.【答案】A【解析】样本中心点为,计算得,代入验证可知选项正确.5. 如图所示的三视图表示的几何体的体积为,则该几何体的外接球的表面积为()A. B. C. D.【答案】C【解析】由三视图可得该几何体为底面边长为,一条侧棱垂直底面的四棱锥,设高为4,则,将该几何体补成一个长方体,则其外接球半径为故这个几何体的外接球的表面积为.故选C.【点睛】本题考查了由三视图,求体积和表面积,其中根据已知的三视图,判断几何体的形状是解答的关键.属于中档题.6. 《九章算术》是我国古代一部数学名著,某数学爱好者阅读完其相关章节后编制了如图的程序框图,其中表示除以的余数,例如.若输入的值为8时,则输出的值为()A. 2B. 3C. 4D. 5【答案】B【解析】模拟执行程序框图,可得:满足条件,满足条件满足条件,不满足条件,,满足条件,满足条件,…,可得:2, 4, 8,∴共要循环3次,故.故选B.7. 已知,则、、的大小排序为()A. B.C. D.【答案】A【解析】为正实数,且,可得:即因为函数单调递增,∴.故选A.8. 以等腰直角三角形的斜边上的中线为折痕,将与折成互相垂直的两个平面,得到以下四个结论:①平面;②为等边三角形;③平面平面;④点在平面内的射影为的外接圆圆心.其中正确的有()A. ①②③B. ②③④C. ①②④D. ①③④【答案】C【解析】由于三角形为等腰直角三角形,故,所以平面,故①正确,排除选项.由于,且平面平面,故平面,所以,由此可知,三角形为等比三角形,故②正确,排除选项.由于,且为等边三角形,故点在平面内的射影为的外接圆圆心, ④正确,故选.9. 已知双曲线的离心率为,其一条渐近线被圆截得的线段长为,则实数的值为()A. 3B. 1C.D. 2【答案】D【解析】双曲线的离心率为,则故其一条渐近线不妨为,圆的圆心,半径为2,双曲线的一条渐近线被圆截得的线段长为,可得圆心到直线的距离为:故选D.10. 已知函数,若,使得成立,则实数的取值范围是()A. B. C. D.【答案】A【解析】由于,函数为增函数,且,函数为奇函数,故,即在上存在.画出的图象如下图所示,由图可知, ,故选.【点睛】本小题主要考查函数的单调性与奇偶性,考查利用导数研究函数的单调性,考查恒成立问题的解题思路.给定一个函数的解析式,首先要分析这个函数的定义域,单调性与奇偶性等等性质,这些对于解有关函数题目可以有个方向,根据基本初等函数的单调性要熟记.11. 如图,过抛物线的焦点作倾斜角为的直线,与抛物线及其准线从上到下依次交于、、点,令,,则当时,的值为()A. 3B. 4C. 5D. 6【答案】C【解析】设,则又,可得同理可得,故选B.12. 已知、是函数(其中常数)图象上的两个动点,点,若的最小值为0,则函数的最大值为()A. B. C. D.【答案】B【解析】由题,当点、分别位于分段函数的两支上,且直线分别与函数图像相切时,最小,设当时,直线因为点在直线直线上,解得同理可得则,且函数在上单调递增,在上单调递见,故函数的最大值为.故选B.第Ⅱ卷(非选择题共90分)二、填空题:共4小题,每小题5分,共20分.将答案填在答题卡上.13. 已知实数,满足条件,则的最大值为__________.【答案】8【解析】画出可行域如图所示,则当目标函数y经过点时取代最大值,即答案为4.14. 为弘扬我国优秀的传统文化,某小学六年级从甲、乙两个班各选出7名学生参加成语知识竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83,则的值为__________.【答案】【解析】,解得,根据中位数为,可知,故.15. 如图,在三角形中,、分别是边、的中点,点在直线上,且,则代数式的最小值为__________.【答案】【解析】不妨设为直角,且,以分别为轴,此时为点的坐标,表示到原点的距离,最短时为点到直线的距离,由于是中位线,故最短的等于点到距离的一半,即.16. 已知中,角、、所对的边分别是、、且,,,若为的内心,则的面积为__________.【答案】【解析】由于,所以,展开化简得.由正弦定理得,所以,解得.设,设外切圆半径为,根据海伦公式有,解得,故.【点睛】本小题主要考查正弦定理和余弦定理解三角形,考查了三角形的面积公式,包括海伦公式及有关内切圆的面积公式.首先根据,及,得到,利用两角和与差的正弦公式和二倍角公式,化简这个式子可求得的值.利用海伦公式可求得面积.三、解答题:解答应写出文字说明、证明过程或演算步骤.17. 已知数列满足,.(1)求证:数列为等比数列;(2)求数列的前项和.【答案】(1)见解析;(2).【解析】【试题分析】(1)利用配凑法将已知配凑成等比数列的形式,由此证得为等比数列.(2)由(1)求得的通项公式,利用裂项求和法求得数列的前项和.【试题解析】(1)∵,∴.又,∴,.∴是以2为首项,2为公比的等比数列.(2)由(1)知,∴,∴.18. 省环保厅对、、三个城市同时进行了多天的空气质量监测,测得三个城市空气质量为优或良的数据共有180个,三城市各自空气质量为优或良的数据个数如下表所示:城城城优(个)28良(个)3230已知在这180个数据中随机抽取一个,恰好抽到记录城市空气质量为优的数据的概率为0.2.(1)现按城市用分层抽样的方法,从上述180个数据中抽取30个进行后续分析,求在城中应抽取的数据的个数;(2)已知,,求在城中空气质量为优的天数大于空气质量为良的天数的概率.【答案】(1)9;(2).【解析】【试题分析】(1)由计算出,再由总数计算出,按比例计算得应抽人数.(2) 由(1)知,且,,利用列举法和古典概型计算公式计算得相应的概率.【试题解析】(1)由题意得,即.∴,∴在城中应抽取的数据个数为.(2)由(1)知,且,,∴满足条件的数对可能的结果有,,,,,,,共8种.其中“空气质量为优的天数大于空气质量为良的天数”对应的结果有,,共3种.∴在城中空气质量为优的天数大于空气质量为良的天数的概率为.19. 如图,在四棱锥中,底面为菱形,,平面,,点、分别为和的中点.(1)求证:直线平面;(2)求点到平面的距离.【答案】(1)见解析;(2).【解析】【试题分析】(1) 取的中点,连结、,通过证明四边形为平行四边形,得到,由此证得平面.(2)利用等体积法,通过建立方程,由此求得点到面的距离.【试题解析】(1)取的中点,连结、,由题意,且,且,故且,所以,四边形为平行四边形,所以,,又平面,平面,所以,平面.(2)设点到平面的距离为.由题意知在中,,在中,在中,故,,,,所以由得:,解得.20. 已知椭圆:的两个焦点与短轴的一个端点构成的三角形的面积为,且椭圆的离心率为.(1)求椭圆的方程;(2)过点且斜率不为零的直线与椭圆交于两点、,点,试探究:直线与的斜率之积是否为常数.【答案】(1);(2)见解析.【解析】【试题分析】(1)根据三角形面积公式和离心率建立方程,解方程组可求得的值.(2)设出直线的方程联立直线的方程和椭圆的方程,写出韦达定理,通过计算.化简后可得为常数...................【试题解析】(1)由题意得(其中椭圆的半焦距),解得.所以椭圆的方程为:.(2)由题意设直线的方程为:,,,由得:,所以,故,,(常数).21. 已知函数.(1)若是的一个极值点,求的最大值;(2)若,,都有,求实数的取值范围.【答案】(1);(2).【解析】【试题分析】(1)求出函数的导数,通过求得的值,根据单调区间求得函数的最大值.(2)将原不等式转化为,构造函数,对求导,对两者比较大小,分成两类,利用分离常数法求得的取值范围.【试题解析】(1),由题意得,即,所以,所以,当时,;当时,,所以在上单调递增,在上单调递减.所以.(2)由题意得,都有,令函数,当时,在上单调递增,所以在上恒成立,即在上恒成立,令,,则,所以在上单调递减,故,所以实数的取值范围为.同理,当时,在上单调递减,所以在上恒成立,即在上恒成立,令,,则,所以在上单调递减,故.所以实数的取值范围为,综上,实数的取值范围为.【点睛】本小题主要考查函数导数与极值,考查函数导数与不等式恒成立问题. 与函数最值有关的参数范围问题,往往利用导数研究函数的单调区间和极值点,并结合特殊点,从而判断函数的大致图像,讨论其图象与轴的位置关系,进而确定参数的取值范围;或通过对方程等价变形转化为两个函数图象的交点问题.请考生在22、23两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的第一题记分,做答时,请用2B铅笔在答题卡上将所选题号后的方框涂黑.22. 在平面直角坐标系中,直线:(为参数),以坐标原点为极点,轴正半轴为极轴,建立极坐标系,曲线:.(1)求直线的极坐标方程及曲线的直角坐标方程;(2)记射线与直线和曲线的交点分别为点和点(异于点),求的最大值.【答案】(1)直线的极坐标方程为:,曲线的直角坐标方程为:;(2).【解析】试题分析:(1)根据极坐标方程、参数方程与普通方程的对应关系即可得出答案;(2)由(1),,所以,即可得到的最大值.试题解析:(1)由题意得直线的普通方程为:,所以其极坐标方程为:.由得:,所以,所以曲线的直角坐标方程为:.(2)由题意,,所以,由于,所以当时,取得最大值:.23. 已知函数.(1)解关于的不等式;(2)若关于的不等式的解集非空,求实数的取值范围.【答案】(1);(2).【解析】试题分析:(1)由题意或,由此可解不等式;(2)由于关于的不等式的解集非空,函数的最小值为-1,由此解得的范围.试题解析:(1)由题意或,所以或,即或,或或,故原不等式的解集为.(2),由于,所以当时,的最小值为-1.所以实数的取值范围为:.【点睛】本题主要考查绝对值的意义,绝对值不等式的解法,体现了等价转化的数学思想,属于中档题。