水力学第四章第一部分
- 格式:ppt
- 大小:1.22 MB
- 文档页数:76

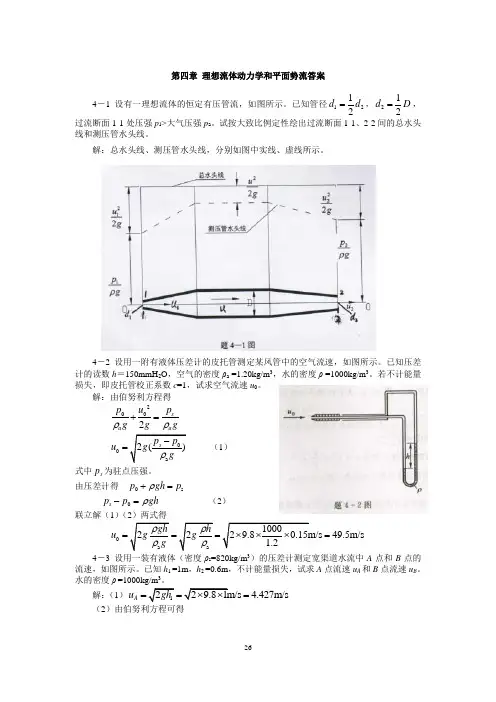
第四章 理想流体动力学和平面势流答案4-1 设有一理想流体的恒定有压管流,如图所示。
已知管径1212d d =,212d D =,过流断面1-1处压强p 1>大气压强p a 。
试按大致比例定性绘出过流断面1-1、2-2间的总水头线和测压管水头线。
解:总水头线、测压管水头线,分别如图中实线、虚线所示。
4-2 设用一附有液体压差计的皮托管测定某风管中的空气流速,如图所示。
已知压差计的读数h =150mmH 2O ,空气的密度ρa =1.20kg/m 3,水的密度ρ =1000kg/m 3。
若不计能量损失,即皮托管校正系数c =1,试求空气流速u 0。
解:由伯努利方程得2002s a a p u p g g gρρ+= 00a 2()s p p u g gρ-=(1) 式中s p 为驻点压强。
由压差计得 0s p gh p ρ+=0s p p gh ρ-= (2)联立解(1)(2)两式得0a a 10002229.80.15m/s 49.5m/s 1.2gh h u gg g ρρρρ===⨯⨯⨯= 4-3 设用一装有液体(密度ρs =820kg/m 3)的压差计测定宽渠道水流中A 点和B 点的流速,如图所示。
已知h 1 =1m ,h 2 =0.6m ,不计能量损失,试求A 点流速u A 和B 点流速u B 。
水的密度ρ =1000kg/m 3。
解:(1)1229.81m/s 4.427m/s A u gh ==⨯⨯= (2)由伯努利方程可得22A AA u p h g gρ+= (1)22B BB u p h g gρ+= (2)式中A h 、A p 和B h 、B p 分别为A 点和B 点处的水深和驻点压强。
由(1)、(2)式可得2222A B A BA B p p u u h h g g gρ-=+-- (3) 由压差计得,22ρρρρ--++=A A s B B p gh gh gh gh p ,所以220.82A BA B p p h h h h gρ-=+-- (4) 由(3)式、(4)式得2222 4.427(10.82)0.6(10.82)0.8922229.8B A u u h g g =--=--=⨯ 29.80.892m/s 4.18m/s B u =⨯⨯=。






4.3水在变直径竖管中流动,已知粗管直径1d =300mm ,流速1v =6s m /。
为使两断面的压力表读值相同,试求细管直径(水头损失不计)。
解: 以过下压力表处的水平面为基准面,列伯努利方程如下:22111222121222w p v p v z z h g g g gααρρ-++=+++∵120w h -=,13z =m ,20z = 取12αα=,当12p p =时,有:222211229.8073694.842v gz v =+=⨯⨯+=29.74v =(m/s )由连续性方程 2211v A vA = ∴2300235.5d d ===(mm ) 答:细管直径为235.5mm 。
4-4 一变直径的管段AB ,直径A d =0.2m ,B d =0.4m ,高差h ∆=1.5m ,今测得A p =302/m kN ,B p =402/m kN , B 处断面平均流速B v =1.5s m /.。
试判断水在管中的流动方向。
解: 以过A 的水平面为基准面,则A 、B 点单位重量断面平均总机械能为:42323010 1.0 1.50.40 4.89210009.80729.8070.2A A A A A p v H z g g αρ⨯⨯⎛⎫=++=++⨯= ⎪⨯⨯⎝⎭(m )2324010 1.0 1.51.5 5.69210009.80729.807B B B B B p v H z g g αρ⨯⨯=++=++=⨯⨯(m )∴水流从B 点向A 点流动。
答:水流从B 点向A 点流动。
4-5 利用皮托管原理,测量水管中的点速度v 。
如读值h ∆=60mm ,求该点流速。
解: 3.85u ====(m/s )u m/s。
答:该点流速 3.85D d4-13 3d=0.1m,水头损失不计,求水流作用在喷嘴上的力。
D d解:(1)取过轴线的水平面为基准面,列螺栓断面与出口断面的伯努利方程:2211122022p v v g g gααρ+=+∴()4222211212122v d p v v d ρρ⎡⎤⎛⎫⎢⎥=-=- ⎪⎢⎥⎝⎭⎣⎦()22100050.93 3.181291.8542=⨯-=(kPa ) 1210.44 3.180.4Q v A π⨯===⨯(m/s ) 2220.4450.930.1Q v A π⨯===⨯(m/s ) (2)取控制体如图所示,列动量方程。


第四章+水轮机的空化与空蚀第四章水轮机的空化与空蚀第一节水流的空化一、水流的空化现象认识到空化空蚀的破坏:发现轮船高速金属螺旋桨在很短时间内就被破坏。
固体围绕固定位置振动液体质点位置易迁移常温下液体质点会从液体中离析,取决于该种液体的汽化特性。
标准大气压力下,水温达到100℃时,发生沸腾汽化;当周围环境压力降低到0.24mH2O时,发生空化现象。
由于液体具有汽化特性:液体汽化:1、恒压加热;2、恒温降压沸腾:液体在衡定压力下加热,当温度高于某一温度时,液体开始汽化形成汽泡。
空化:当液体温度一定,降低压力到某一临界压力时,液体也会汽化或溶解于液体中的空气发育形成空穴。
气蚀现象:包括空化和空蚀两个过程。
空化:液体中形成空穴使液相流体的连续性遭到破坏,发生在压力下降到某一临界值的流动区域,空穴中主要充满着液体的蒸汽以及从溶液中析出的气体。
可以发生在液体内部,也可以发生在固定边界上。
空蚀:当空穴进入压力较低的区域时,就开始发育成长为较大的气泡,然后气泡被流体带到压力高于临界值的区域,气泡就将溃灭,在空泡溃灭过程中伴随着机械、电化、热力、化学等过程的作用,引起过流表面的材料损坏。
只发生在固体边界上。
空蚀是空化的直接后果。
水轮机气蚀:水流通过水轮机时,如果某些地方流速增高了,根据水力学能量方程,必然引起该处的局部压力降低,如果该处水流速度增加很大,以致使压力降低到在该水温下的汽化压力时,则此低压区的水开始汽化,便会产生气蚀。
水轮机的空化现象是水流在能量转换过程中产生的特殊现象。
二、空蚀机理空蚀的形成与水的汽化现象有密切的联系。
水的汽化压力:在给定温度下水开始汽化的临界压力。
水在各种温度下的汽化压力值水的温度(℃)汽化压力(mH2O) 0 0.06 5 0.09 10 0.12 20 0.24 30 0.43 40 0.72 50 1.26 60 2.03 70 3.18 80 4.83 90 7.15 100 10.33空蚀对金属材料表面的侵蚀破坏有机械作用、化学作用和电化作用三种,以机械作用为主。

1.平板边界层
✧平板上满足无滑移条件,u=0;
✧沿平板法线方向,流速很快增大到来流速度U0;
✧平板以上存在两个性质不同的流动区域:必须考虑粘性的
边界层;粘性可以忽略,相当于理想液体的边界层外的流动;
✧边界层在平板前缘处厚度为零,随流动距离增加而增加;
✧随着流速梯度由大边小,边界层内也存在层流和紊流两种
流态,在紊流区同样存在层流底层(粘性底层);
✧管道进口段的边界层
2.曲面边界层及其分离现象
圆柱面上
DE段:加速减压,压能向动能转化并克服摩阻力做功;
E点之后:减速加压,动能转化为压能并继续克服摩阻力做功;
S点:由于摩阻耗能和逆压的双重作用,此处流速为零。
由于连续性,质点立即被外侧流动所带走,边界层在此分离;SF段:形成回流并发展成旋涡,消耗大量能量;
F点:压强小于D点压强。
✧压差阻力:
摩阻耗能和旋涡耗能使得尾流区(边界层下游形成的旋涡区)物体表面的压强低于来流压强,形成压差阻力,因与物体形状有很大关系,也称形状阻力。
分离点越靠近下游,或尾流区越小,压差阻力就越小。
✧卡门涡街:
尾流的形态变化主要取决于来流的雷诺数,见下图:
雷诺数达到一定数值时,旋涡从物体下游两侧交替脱落,排成两列带往下游,称之卡门涡街。
卡门涡街使物体受到交替变向的横向力。
当雷诺数继续增大,规则的卡门涡街消失代之以随机的紊流运动。
第四章 思考题:4-1:N-S 方程的物理意义是什么?适用条件是什么?物理意义:N-S 方程的精确解虽然不多,但能揭示实际液体流动的本质特征,同时也作为检验和校核其他近似方程的依据,探讨复杂问题和新的理论问题的参考点和出发点。
适用条件:不可压缩均质实际液体流动。
4-2 何为有势流?有势流与有旋流有何区别?答:从静止开始的理想液体的运动是有势流. 有势流无自身旋转,不存在使其运动的力矩.4—3 有势流的特点是什么?研究平面势流有何意义?有势流是无旋流,旋转角速度为零。
研究平面势流可以简化水力学模型,使问题变得简单且于实际问题相符,通过研究平面势流可以为我们分析复杂的水力学问题。
4-4.流速势函数存在的充分必要条件是流动无旋,即xu y u yx ∂∂=∂∂时存在势函数,存在势函数时无旋。
流函数存在的充分必要条件是平面不可压缩液体的连续性方程,即就是0=∂∂+∂∂yu x u yx存在流函数。
4—5何为流网,其特征是什么?绘制流网的原理是什么 ?流网:等势线(流速势函数的等值线)和流线(流函数的等值线)相互正交所形成的网格 流网特征:(1)流网是正交网格(2)流网中的每一网格边长之比,等于流速势函数与流函数增值之比。
(3)流网中的每个网格均为曲线正方形 原理:自由表面是一条流线,而等势线垂直于流线。
根据入流断面何处流断面的已知条件来确定断面上 流线的位置。
4-6.利用流网可以进行哪些水力计算?如何计算?解:可以计算速度和压强。
计算如下:流场中任意相邻之间的单宽流量∆q 是一常数。
在流场中任取1、2两点,设流速为,,两端面处流线间距为∆m1,∆。
则∆q=∆m1=∆,在流网中,各点处网格的∆m 值可以直接量出来,根据上式就可以得出速度的相对变化关系。
如果流畅中某点速度已知,就可以其他各点的速度。
流畅中的压强分布,可应用能量方程求得。
z1++=++当两点位置高度z1和为已知,速度,u2已通过流亡求出时,则两点的压强差为-=-+-如果流畅中某一点压强已知,则其他个点压强均可求得4.7利用流网计算平面势流的依据是什么?(参考4.6的解释)4-8流网的形状与哪些因素有关?网格的疏密取决于什么因素?答:流网由等势线和流线构成,流网的形状与流函数φ(x,y)和流速势函数ψ(x,y)有关;由∆q=∆ψ=常数,∆q=u1∆m1=常数,得两条流线的间距愈大,则速度愈小,若间距愈小,则速度愈大。
4-1如图 4-26 所示,在一管路上测得过流断面1-1的测压管高度 g 为1.5m ,过流面积A 1为0.05m 2;过流断面 2-2的面积 A 2为 0.02m 2;两断面间水头损失量 Q 为 20l/s ; z 1为 2.5m , z 2为 2.0m 。
试求断面 2-2 的测压管高度 p 2 。
(提示:注意流动12g方向)。
解:依题知Q 20l s 0.02m 3 s由连续性方程知断面 1-1 和断面 2-2 的平均流速Q 0.02 v 22 A 2 0.021-1 和断面 2-2 水流可近似看做渐变流,以图示水平面0-0 为基准面,列两断面的总流能量方程22Z 1Pg121v g 1 Z 2Pg222g v 2h w1g 2g2g2gw令动能修正系数 1 2 1,p2z1 z2p1v1 v 20.5 v 12.5 2 1.5(0.41 )0.5(0.4)1.953mg1 2g2g 2g2 9.82 9.84-2 如图 4-27 所示,从水面保持恒定不变的水池中引出一管路, 水流在管路末端流入大气, 管路由三段直径不等的管道组成,其过水面积分别是 A 1=0.05m 2, A 2=0.03m 2, A 3=0.04m 2,若水池容积很大,行近流速可以忽略( v 0≈0),当不计管路的水头损失时,试求: ( 1)出口2h 0.52gv1A 10.020.4m s 0.051m s因管路直径直径变化缓慢,断面流速 v 3 及流量 Q ;(2)绘出管路的测压管水头线及总水头线。
如图选择管轴线为 0-0 基准面,对水池的水面 1-1 和管路出口断面 2-2 应用能量方程, 列两断面的总流能量方程22h p1o v o2h4 p 43v 32g 2g 4g 2g令动能修正系数 o 3 1,由于选择管轴线为 0-0 基准面,水池的水面和管路出口断面的相对压强P 1 0 ,P 4 0且h 5,h 4 02h 0 0 0 0 v32g故v 3 2gh 2 9.8 5 9.899m sQ v 3A 3 9.899 0.04 0.396m 3 s( 2)测压管水头线 (虚线)及总水头线 (实线 )由题知,断面 A1 处的流速 v1 Q 0.396 7.92m s 和断面 A2 处的流速 A 1 0.05Q 0.396 A 2 0.03解:(1)依题知A 3vA 2总水头线v0A1A2 A34-3 在水塔引出的水管末端连接一个消防喷水枪,将水枪置于和水塔液面高差H 为10m 的地方,如图4-28 所示。