4第四单元思维导图
- 格式:doc
- 大小:39.00 KB
- 文档页数:1


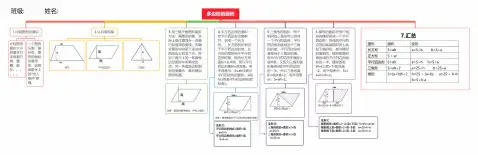
多边形的面积1.比较图形的面积①比较图形面积大小的基本方法有数方格、重叠、割补。
②一个图形分割、移补后,图形的面积没有改变,这就是数学上的“出入相补”原理。
2.认识底和高3.用三角尺画图形高的方法:画图形的高,实际上是过直线外一点画已知直线的垂线。
先确定图形中的某个顶点或图形边上的某个点,然后三角尺上的一条直角边过图形中所确定的点,另一条直角边和图形的底重合,最后画出图形的高。
注意:画高时要用虚线,并标上垂足。
4.平行四边形的面积:把平行四边形沿高剪开,拼成一个长方形,,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高,因为长方形面积=长X宽,所以平行四边形面积=底X高。
用字母表示:S=ah(S表示平行四边形的面积,a和h分别是平行四边形的底和高)。
注意:等底等高的平行四边形的面积相等变形式:平行四边形的底=面积÷高a=S÷h平行四边形的高=面积÷底h=S÷a5.三角形的面积:两个相同的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底,平行四边形的高相当于三角形的高,因为平行四边形的面积=底X高,又因为三角形面积是拼成的平行四边形的一半,所以三角形面积=底X高÷2,用字母表示:S=ah÷2。
变形式:三角形的底=面积×2÷高a=2S÷h三角形的高=面积×2÷底h=2S÷a6.梯形的面积:把两个相同的梯形拼成一个平行四边形,拼成的平行四边形的底是梯形的上底和下底的和,高与梯形的高相同,梯形的面积是拼成的平行四边形面积的一半。
梯形的面积=(上底+下底)X高÷2,用字母表示:S=(a+b)×h÷2。
变形式梯形的高=面积×2÷(上底+下底) h=2S÷(a+b) 梯形的上底=面积×2÷高-下底 a=2S÷h-b 梯形的下底=面积×2÷高-上底 a=2S÷h-a7.汇总。

多边形的面积1.比较图形的面积①比较图形面积大小的基本方法有数方格、重叠、割补。
②一个图形分割、移补后,图形的面积没有改变,这就是数学上的“出入相补”原理。
2.认识底和高3.用三角尺画图形高的方法:画图形的高,实际上是过直线外一点画已知直线的垂线。
先确定图形中的某个顶点或图形边上的某个点,然后三角尺上的一条直角边过图形中所确定的点,另一条直角边和图形的底重合,最后画出图形的高。
注意:画高时要用虚线,并标上垂足。
4.平行四边形的面积:把平行四边形沿高剪开,拼成一个长方形,,长方形的长相当于平行四边形的底,长方形的宽相当于平行四边形的高,因为长方形面积=长X宽,所以平行四边形面积=底X高。
用字母表示:S=ah(S表示平行四边形的面积,a和h分别是平行四边形的底和高)。
注意:等底等高的平行四边形的面积相等变形式:平行四边形的底=面积÷高a=S÷h平行四边形的高=面积÷底h=S÷a5.三角形的面积:两个相同的三角形可以拼成一个平行四边形,平行四边形的底相当于三角形的底,平行四边形的高相当于三角形的高,因为平行四边形的面积=底X高,又因为三角形面积是拼成的平行四边形的一半,所以三角形面积=底X高÷2,用字母表示:S=ah÷2。
变形式:三角形的底=面积×2÷高a=2S÷h三角形的高=面积×2÷底h=2S÷a6.梯形的面积:把两个相同的梯形拼成一个平行四边形,拼成的平行四边形的底是梯形的上底和下底的和,高与梯形的高相同,梯形的面积是拼成的平行四边形面积的一半。
梯形的面积=(上底+下底)X高÷2,用字母表示:S=(a+b)×h÷2。
变形式梯形的高=面积×2÷(上底+下底) h=2S÷(a+b) 梯形的上底=面积×2÷高-下底 a=2S÷h-b 梯形的下底=面积×2÷高-上底 a=2S÷h-a7.汇总。


初中上学期第四单元数学思维导图图片4、1几何图形1、几何图形:从形形色色的物体外形中得到的图形叫做几何图形。
2、立体图形:这些几何图形的各部分不都在同一个平面内。
3、平面图形:这些几何图形的各部分都在同一个平面内。
立体图形中一些部分是平面图形。
5、三视图:从左面看,从正面看,从上面看6、展开图:有些立体图形是由一些平面图形围成的,将它们的表面适当剪开,可以展开成平面图形。
这样的平面图形称为相应立体图形的展开图。
7、⑴几何体简称体;包围着体的是面;面面相交形成线;线线相交形成点;⑵点无大小,线、面有曲直;⑶几何图形都是由点、线、面、体组成的;⑷点动成线,线动成面,面动成体;⑸点:是组成几何图形的基本元素。
4、2直线、射线、线段1、直线公理:经过两点有一条直线,并且只有一条直线。
即:两点确定一条直线。
2、当两条不同的直线有一个公共点时,我们就称这两条直线相交,这个公共点叫做它们的交点。
3、把一条线段分成相等的两条线段的点,叫做这条线段的中点。
4、线段公理:两点的所有连线中,线段做短(两点之间,线段最短)。
5、连接两点间的线段的长度,叫做这两点的距离。
6、直线的表示方法:如图的直线可记作直线AB或记作直线m。
(1)用几何语言描述右面的图形,我们可以说:点P在直线AB外,点A、B都在直线AB上。
(2)如图,点O既在直线m上,又在直线n上,我们称直线m、n相交,交点为O。
7、在直线上取点O,把直线分成两个部分,去掉一边的一个部分,保留点0和另一部分就得到一条射线,如图就是一条射线,记作射线OM或记作射线a。
注意:射线有一个端点,向一方无限延伸。
8、在直线上取两个点A、B,把直线分成三个部分,去掉两边的部分,保留点A、B和中间的一部分就得到一条线段。
如图就是一条线段,记作线段AB或记作线段a。
注意:线段有两个端点。
4、3角1、角的定义:有公共端点的两条射线组成的图形叫角。
这个公共端点是角的顶点,两条射线为角的两边。