第四单元思维导图

人教版小学数学四年级上册18单元思维导图一、第一单元：认识更大的数1. 数位顺序表2. 整数的读法和写法3. 整数的比较和大小关系4. 整数的加减法5. 乘法口诀表二、第二单元：角的初步认识1. 角的概念2. 角的分类3. 角的度量4. 角的加减法5. 角的周长三、第三单元：观察物体与几何图形1. 长方形和正方形的特征2. 三角形的特征3. 四边形的特征4. 圆的特征5. 立体图形的特征四、第四单元：分数的初步认识1. 分数的概念2. 分数的读法和写法3. 分数的比较和大小关系4. 分数的加减法5. 分数的应用五、第五单元：两位数乘两位数1. 乘法口诀表的应用2. 两位数乘两位数的计算方法3. 两位数乘两位数的进位和借位4. 两位数乘两位数的估算5. 两位数乘两位数的应用六、第六单元：小数的初步认识1. 小数的概念2. 小数的读法和写法3. 小数的比较和大小关系4. 小数的加减法5. 小数的应用七、第七单元：简易方程1. 方程的概念2. 方程的解法3. 方程的应用4. 一元一次方程5. 方程的变形八、第八单元：观察物体与几何图形（二）1. 立体图形的表面积2. 立体图形的体积3. 立体图形的切割与拼接4. 立体图形的应用5. 立体图形的拓展人教版小学数学四年级上册18单元思维导图一、第一单元：认识更大的数1. 数位顺序表：掌握数位的名称和顺序，了解数位之间的关系。

2. 整数的读法和写法：学习如何正确地读出和写出整数，掌握整数的基本表达方式。

3. 整数的比较和大小关系：通过比较整数的大小，建立数的大小概念，培养逻辑思维能力。

4. 整数的加减法：掌握整数加减法的计算方法，能够熟练地进行整数加减运算。

5. 乘法口诀表：学习乘法口诀表，掌握乘法的基本规律，提高计算速度和准确性。

二、第二单元：角的初步认识1. 角的概念：理解角的概念，掌握角的定义和特征。

2. 角的分类：学习不同类型的角，如锐角、直角、钝角等，了解它们之间的区别和联系。

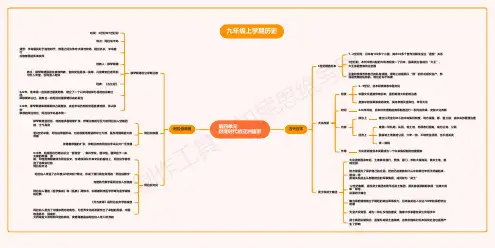
第四单元封建时代的亚洲国家古代日本6世纪前的日本1~2世纪时，日本有100多个小国，其中30多个曾与汉朝发生过“通使”关系5世纪时，本州中部兴起的大和政权统一了日本，最高统治者成为“大王”，大王依靠贵族统治全国王室和贵族各有自己的私有领地，领地上的居民以“部”的形式组织生产，部民是贵族的私有民，地位近似于奴隶大化改新背景6~9世纪，日本积极吸收中国文化中国文化直接影响日本，强烈刺激大和的统治者皇族中的改革派发动政变，扶持孝德天皇即位，年号大化时间646年开始，日本仿效唐朝的典章制度进行一系列的改革，史称大化改新内容政治上建立以天皇为中心的中央集权制度，地方设国、郡、里三级，由中央派管理治理经济上废除一切私地，私民，将土地、部民收归国有，成为公地、公民国家将土地攽给公民，六年一放，不能终生使用，也不能买卖统一赋税作用大化改新使日本发展成为一个中央集权制的封建国家武士和武士集团大化改新百余年后，土地兼并盛行，贵族、豪门、寺院大量购买、兼并土地，组成庄园地方豪强为了保护自己的庄园，把自己的家族和仆从中的青壮年男子武装起来，组成一种血缘关系的主从制相结合的军事集团，成员称为“武士”12世纪晚期，源氏武士集团击败平氏武士集团，源氏首领源赖朝获得“征夷大将军”称号，设幕府于镰仓镰仓幕府拥有独立于朝廷的政治军事权力，日本由此进入长达700年的幕府统治时期天皇大权旁落，成为一种礼仪性的摆设。

国家大权掌握在武士阶层手中武士集团长期统治，逐渐形成武土道精神。

这种价值观对日本民间社会也逐渐产生了影响阿拉伯帝国穆罕默德创立伊斯兰教时间：6世纪末7世纪初地点：阿拉伯半岛背景：半岛居民处于游牧时代，部落之间为争夺水源与牧场，相互仇杀；半岛盛行氏族部落的多神崇拜创教人：穆罕默德教义：穆罕默德最初在麦加传教，宣扬安拉是独一真神，凡信奉安拉者死后可升入天堂，否则堕入地狱经典：《古兰经》622年，他率领一些信徒迁居麦地那，建立了一个以共同信仰为基础的宗教社团，即穆斯林公社。

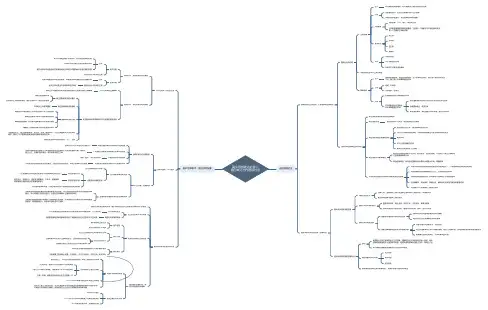
高中思想政治必修二第四单元当代国际社会走近国际社会国际社会的主要成员：主权国家和国际组织国际社会的构成主权国家含义对内具有最高管辖权，对外具有独立权的国际社会成员分类按国家性质分：社会主义国家和资本主义国家按经济发展程度分：发达国家和发展中国家构成要素构成要素：人口、领土、政权和主权主权是最重要的国家构成要素：主权是一个国家不可分割的最高权力，是一个国家的生命和灵魂基本权利独立权平等权自卫权管辖权义务不侵犯别国不干涉他国的内政以和平方式解决国际争端未被国际社会承认主权的地区国际组织含义国际组织是国家、地区或民间团体，出于各种特定目的，通过签订条约或协议的方式，建立有一定规章制度的团体分类政府、非政府世界性的、区域性作用对国际组织的作用要做具体分析许多国际组织在国际社会中发挥重要的作用促进国家间的政治经济文化科学技术的交流与合作协调国际政治、经济关系调节国际争端，缓和国家之间的矛盾，维护世界和平活跃在联合国舞台上的中国联合国是世界性政府间的国际组织联合国的宗旨维护国际和平与安全，促进国际合作与发展联合国会员国应遵循的原则各会员国主权平等，履行宪章规定的义务以和平方式解决国际争端，不得对其他国家进行武力威胁或使用武力集体协作不干涉任何国家的内政确保非会员国遵守上述原则联合国的作用和局限性联合国在维护世界和平与安全，促进经济、社会的发展，以及实行人道主义援助等方面发挥着积极作用联合国局限性：如何适应国际形势发展以发挥更大作用，需要改革中国在联合国的活动表明中国是负责任的国家中国作为联合国的创始国和安理会常任理事国之一，一贯遵循联合国的宗旨和原则支持按照联合国宪章精神进行工作，支持联合国的改革积极参加联合国及其专门机构有利于世界和平与发展的活动在世界裁军、环境保护，保障人权、解决地区冲突等方面发挥重要作用对世界和平与发展做出了重大的贡献国际关系的决定性因素：国家利益国际关系及其决定因素国际关系的含义国家之间，国际组织之间以及国家与国际组织之间的关系，叫国际关系最主要是国家与国家之间的关系国际关系的内容和形式国际关系内容：政治关系、经济关系、文化关系、军事关系等国际关系的形式是多样的。

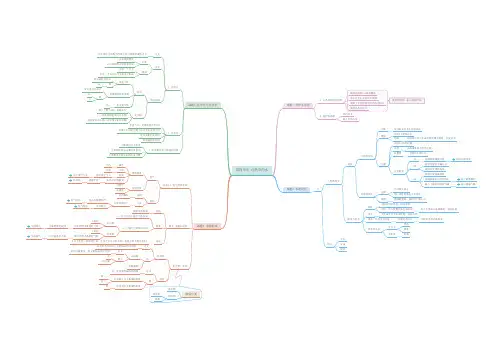
要节约用水，防止水体污染第四单元 自然界的水课题1 爱护水资源课题2 水的净化课题3 水的组成课题4 化学式与化合价人类拥有的水资源1.爱护水资源2.化学式1.化合价2.有关相对分子质量的计算3.地球表面约71%被水覆盖海水中含有大量化学资源地球上可供直接使用的淡水较少我国人均水量少节约用水防止水体污染水自然界的水纯水不溶性杂质可溶性杂质沉降吸附过滤蒸馏过滤例：活性炭除去水中臭味可以除去部分可以除去较大不溶性杂质明矾明矾溶于水后生成的胶状物会吸附、沉淀杂质实验4-2水的过滤实验4-1明矾净水目的分离液体和不溶性杂质注意事项一贴二低三靠滤纸紧贴滤纸内壁加快过滤速度滤纸边缘低于漏斗口液面低于滤纸边缘烧杯口紧靠玻璃棒装置图教材P75 图4-16玻璃棒靠在三层滤纸上漏斗下端防止液体飞溅防止滤纸破损防止液滴飞溅杂质硬水与软水硬水软水含较多可溶性钙、镁化合物不含或含较少可用性钙、镁化合物硬水、软水区分方法用肥皂水区分含较多浮渣的是硬水饮水变软水生活中煮沸暴晒实验室蒸馏加热、长久放置后易生成水垢水垢主要成分是碳酸钙、氢氧化镁蒸馏装置图：教材P77 图4-20无色无味透明实验4-5 氢气燃烧实验探究 电解水试验氢气验纯目的防止爆炸方法点燃少量氢气发出尖锐爆鸣声声音很小氢气不纯氢气较纯物理性质颜色气味无味无色密度比空气小密度向下排空气法排水法难溶于水在水中的溶解度化学性质可燃性还原性目的现象结论化合物、单质探索水的组成1、两个点击上都有气体生成2、生成的气体体积不同连正极连负极1体积2体积用点燃的木条检验气体木条燃烧更剧烈生成氧气用点燃的木条检验气体产生淡蓝色火焰生成氢气水分子含氢、氧两种元素，且每个水分子中含氢、氧原子的个数比为2:1化合物由两种及两种以上元素组成的纯净物单质由一种元素组成的纯净物例氧化物水二氧化碳由氧元素和另一种元素组成的化合物定义定义例子高锰酸钾定义例氧气氢气铁由双原子分子构成的单质直接由原子构成的单质物质分类混合物纯净物化合物单质由元素符号和数字的组合表示物质组成的式子定义意义书写规则宏观微观表示某种物质表示某物质由某元素组成表示一个分子表示一个分子由几个某原子组成单质化合物稀有气体金属和固态非金属非金属气体用元素符号表示用元素符号表示例Ne例FeCO 原子个数为1时，省略不写氧化物的把氧写在右侧金属元素在左侧，非金属元素在右侧单质当中，元素的化合价为0元素在不同化合物中的化合价可能不同常见元素的化合价常见根的化合价计算相对分子质量计算物质组成元素的质量比计算物质中某元素的质量分数。

五年级上册数学第四单元多边形面积思维
导图
多边形面积思维导图多边形面积思维导图是一种指导学生运用数学思维方法来解决多边形面积问题的图表，它包含了多边形面积概念、多边形面积计算方法、多边形面积思维关系等内容。

一、多边形面积概念多边形面积是指一个多边形内部的凹凸的表面积。

它的概念是由等边三角形的面积公式推导而来：S=1/2×a×h ，其中a是三角形的底，h是三角形的高。

二、多边形面积计算方法多边形面积的计算方法主要有三种：（1）边长乘高法：将多边形拆分成多个等边三角形，利用每个三角形的面积公式S=1/2×a×h来计算多边形的面积；（2）公式法：根据不同的多边形，有不同的面积计算公式，如正方形的面积计算公式S=a×a，其中a是正方形的边长；（3）矩形法：将多边形拆分成多个矩形，利用矩形的面积公式S=a×b来计算多边形的面积。

三、多边形面积思维关系多边形面积思维关系应该牢记的是：多边形的面积其实就是所有的三角形面积的和，而每个三角形的面积可以由S=1/2×a×h来计算，因此，多边形面积的公式就可以表示为：S=1/2×（a1×h1+a2×h2+a3×h3+……）。

以上就是多边形面积思维导图的内容，它帮助我们理解了多边形面积的计算方法和思维关系，我们可以根据这个思维导图，把不同的多边形拆分成多个等边三角形或矩形，然后再根据相应的公式来计算它们的面积，最终把它们的面积相加，就可以得到多边形的面积了。

通过多边形面积思维导图，我们可以把复杂的多边形面积计算问题分解成一个一个简单的问题，这样就能更加方便快捷地解决多边形面积问题，同时也增强了我们的数学思维能力。