六年级上第四单元比集体备课思维导图
- 格式:ppt
- 大小:3.17 MB
- 文档页数:16

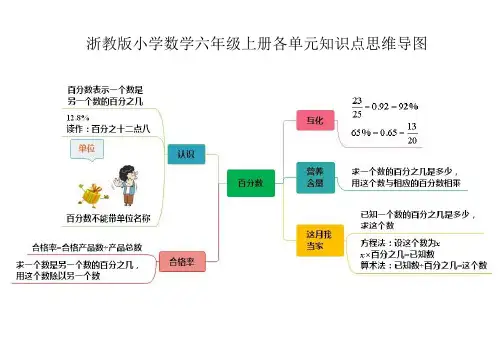
小学数学六年级上册各单元思维导图第一部分:数的认识一、整数1. 自然数:0、1、2、3、4、5、6、7、8、9、10……2. 整数:自然数和它们的相反数3. 整数的分类:正整数、0、负整数二、分数1. 分数的意义:表示一个整体被平均分成若干份,其中的一份或几份2. 分数的表示:分子/分母3. 分数的分类:真分数、假分数、带分数三、小数1. 小数的意义:表示一个整体被平均分成若干份,其中的一份或几份,用小数点表示2. 小数的表示:整数部分和小数部分3. 小数的分类:有限小数、无限小数第二部分:数的运算一、加法1. 整数加法:相同符号的整数相加,异号整数相加2. 分数加法:同分母分数相加,异分母分数相加3. 小数加法:小数点对齐,逐位相加二、减法1. 整数减法:相同符号的整数相减,异号整数相减2. 分数减法:同分母分数相减,异分母分数相减3. 小数减法:小数点对齐,逐位相减三、乘法1. 整数乘法:相同符号的整数相乘,异号整数相乘2. 分数乘法:分子相乘,分母相乘3. 小数乘法:小数点对齐,逐位相乘四、除法1. 整数除法:相同符号的整数相除,异号整数相除2. 分数除法:分子相除,分母相除3. 小数除法:小数点对齐,逐位相除第三部分:数的性质一、数的性质1. 整数的性质:奇数、偶数、质数、合数2. 分数的性质:分子分母同乘(除)一个数,分数的值不变3. 小数的性质:小数点向左(右)移动一位,小数的值缩小(扩大)10倍二、数的运算定律1. 加法交换律:a + b = b + a2. 加法结合律:(a + b) + c = a + (b + c)3. 乘法交换律:a × b = b × a4. 乘法结合律:(a × b) × c = a × (b × c)5. 乘法分配律:a × (b + c) = a × b + a × c三、数的运算顺序1. 先算乘除,后算加减2. 同级运算,从左到右依次计算3. 括号内的运算优先级最高第四部分:数的应用一、整数应用1. 计算长度、面积、体积等2. 解决实际问题,如购物、分配、比较等二、分数应用1. 计算比例、比率等2. 解决实际问题,如分物品、分配资源等三、小数应用1. 计算长度、面积、体积等2. 解决实际问题,如购物、分配、比较等第五部分:几何图形一、平面图形1. 线段、射线、直线:线段是有限长的直线,射线有一个端点,直线无限长2. 角:由两条射线共同确定的图形,有一个顶点和两条边3. 三角形:由三条线段围成的图形,有三个角和三个边4. 四边形:由四条线段围成的图形,有四个角和四个边5. 圆:平面内到一个固定点距离相等的所有点组成的图形二、立体图形1. 长方体:由六个长方形围成的立体图形,有六个面、十二条边和八个顶点2. 正方体:由六个正方形围成的立体图形,有六个面、十二条边和八个顶点3. 圆柱:由两个底面和一个侧面围成的立体图形,底面是圆形4. 圆锥:由一个底面和一个侧面围成的立体图形,底面是圆形5. 球:由一个点向外无限延伸,到该点的距离相等的所有点组成的立体图形第六部分:几何图形的性质一、平面图形的性质1. 线段的性质:线段有长度,线段之间可以比较大小2. 角的性质:角有度数,角之间可以比较大小3. 三角形的性质:三角形的内角和为180度,等腰三角形的底角相等,直角三角形的勾股定理4. 四边形的性质:四边形的内角和为360度,矩形、正方形的对角线互相平分5. 圆的性质:圆的周长与直径的比例是圆周率,圆的面积与半径的平方成正比二、立体图形的性质1. 长方体的性质:长方体的体积等于长、宽、高的乘积2. 正方体的性质:正方体的体积等于边长的立方3. 圆柱的性质:圆柱的体积等于底面积乘以高4. 圆锥的性质:圆锥的体积等于底面积乘以高除以35. 球的性质:球的体积等于半径的立方乘以4/3π第七部分:几何图形的测量一、长度测量1. 线段长度:使用直尺或卷尺进行测量2. 角度测量:使用量角器进行测量二、面积测量1. 平面图形面积:根据公式计算,如长方形面积=长×宽,圆面积=πr²2. 立体图形表面积:根据公式计算,如长方体表面积=2(长×宽+长×高+宽×高)三、体积测量1. 立体图形体积:根据公式计算,如长方体体积=长×宽×高,圆柱体积=底面积×高2. 容器体积:使用量筒或量杯进行测量第八部分:数学应用与拓展一、数学在生活中的应用1. 购物:计算价格、找零等2. 测量:计算长度、面积、体积等3. 分配:分配物品、资源等二、数学在科学中的应用1. 物理学:计算速度、加速度、力等2. 化学:计算物质的量、浓度等3. 生物:计算种群数量、增长率等三、数学在艺术中的应用1. 音乐:计算音高、节奏等2. 绘画:计算比例、透视等3. 建筑设计:计算结构、空间等第九部分:数学问题解决策略一、问题解决步骤1. 理解问题:仔细阅读题目,明确已知条件和求解目标2. 制定计划:根据问题类型和条件,选择合适的解决方法3. 执行计划:按照计划进行计算和推导4. 检查结果:验证计算过程和结果的正确性二、常见问题解决方法1. 图形法:通过绘制图形,直观地表示问题条件,便于理解和解决2. 列表法:将问题条件列成表格,便于分析和比较3. 代数法:使用代数表达式和方程,进行符号运算和推导4. 逻辑推理法:根据已知条件和数学规律,进行逻辑推理和证明第十部分:数学思维培养一、培养逻辑思维能力1. 通过解决数学问题,锻炼逻辑推理和证明能力2. 学习数学定义、定理和公式,理解其背后的逻辑关系二、培养空间想象能力1. 学习几何知识,通过绘制图形和想象空间关系,培养空间想象力2. 参与数学建模活动,将实际问题转化为数学模型,提高空间想象能力三、培养数学建模能力1. 学习数学建模方法,将实际问题转化为数学问题2. 参与数学建模竞赛和活动,提高数学建模能力第十一部分:数学学习资源一、教材和辅导书1. 选择适合自己水平的教材和辅导书,进行系统学习2. 利用辅导书中的例题和习题,巩固所学知识二、在线资源和应用程序1. 利用在线教育平台和数学学习网站,获取丰富的学习资源2. 数学学习应用程序,进行互动式学习和练习三、数学竞赛和活动1. 参与数学竞赛,提高数学水平和竞争意识2. 参加数学讲座、研讨会等活动,拓宽数学视野。

第4讲比(思维导图+知识梳理+例题精讲+易错专练)一、思维导图二、知识点梳理知识点一:比的意义和各个部分的名称1、比:两个数相除也叫两个数的比;2、比式中,比号(∶)前面的数叫前项,比号后面的项叫做后项,比号相当于除号,比的前项除以后项的商叫做比值。
3、比的读法、写法:a比b记作a:b,读作a比b。
4、比表示的是两个数的关系,可以用分数表示,写成分数的形式,读作几比几。
例:12∶20= =12÷20= =0.6 12∶20读作:12比20知识点二:比的基本性质和化简比1、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变,这叫做比的基本性质。
2、化简比化简之后结果还是一个比,不是一个数。
(1)用比的前项和后项同时除以它们的最大公因数。
(2)两个分数的比,用前项后项同时乘分母的最小公倍数,再按化简整数比的方法来化简。
也可以求出比值再写成比的形式。
(3)两个小数的比,可以先把小数比化成整数比,再按整数比的化简方法化简。
知识点三:比的应用按比例分配问题的解决方法:1、已知单位“1”的量用乘法。
2、未知单位“1”的量用除法。
3、分数应用题基本数量关系(把分数看成比)(1)甲是乙的几分之几?甲=乙×几分之几乙=甲÷几分之几几分之几=甲÷乙(2)甲比乙多(少)几分之几?4、画线段图:(1)找出单位“1”的量,先画出单位“1”,标出已知和未知。
(2)分析数量关系。
(3)找等量关系。
(4)列方程。
两个量的关系画两条线段图,部分和整体的关系画一条线段图。
三、例题精讲考点一:比的意义、比各部分的名称【典型一】一根绳子,用去,用去的和剩下的比是3:2,剩下的是总长度的。
【分析】把一根绳子总长度看作5份,用去,也就是用去5×=3份。
据此可求出用去的和剩下的比,再用除法求出剩下的是总长度的几分之几。
【解答】解:5×=3(份)5﹣3=2(份)用去的和剩下的比是3:2。

人教版
六年级上册数学全册思维导图
3、分数除法
4、比7、扇形统计图
9、总复习5、圆
8、数学广角——数与形
6、百分数(一)1、分数乘法
2、位置与方向(二)
第一单元
分数乘法分数乘整数
1、分数乘整数的意义:表示几个相同分数的和
2、计算方法(1、先计算再约分;2、先约分再计算)
分数乘分数
1、分数乘分数的意义:求这个数的几分之几是多少
2、计算方法(1、先计算再约分;2、先约分再计算)
3、分数乘分数的应用
分数乘小数
1、分数化小数
2、小数化分数
分数混合运算
1、没有括号的先算乘法,再算加减法
2、有括号的先算括号里面的,再算括号外面的
分数运算定律整数乘法中的交换律、结合律、分配律在分数运算中同样适用,可以使计算简便
解决问题
1、求一个数的几分之几是多少
2、求比一个数多(或少)几分之几的数是多少
(1)单位“1”的量×【1±这个数量比单位“1”的量多(或少)的几分之几】=这个数量
(2)单位“1”的量±单位“1”的量×这个数比单位“1”的量多(或少)的几分之几=这个数量。

PEP六年级上册unit4复习思维导图(word版可编辑修改)
PEP六年级上册unit4复习思维导图(word版可编辑修改)
编辑整理:
尊敬的读者朋友们:
这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(PEP六年级上册unit4复习思维导图(word版可编辑修改))的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为PEP六年级上册unit4复习思维导图(word版可编辑修改)的全部内容。

六年级数学上册比和比的应用(一)、比的意义1、比的意义:两个数相除又叫做两个数的比。
2、在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
比的前项除以后项所得的商,叫做比值。
例如 15 :10 = 15÷10=3/2(比值通常用分数表示,也可以用小数或整数表示)∶ ∶ ∶ ∶前项比号后项比值3、比可以表示两个相同量的关系,即倍数关系。
也可以表示两个不同量的比,得到一个新量。
例:路程÷速度=时间。
4、区分比和比值比:表示两个数的关系,可以写成比的形式,也可以用分数表示。
比值:相当于商,是一个数,可以是整数,分数,也可以是小数。
5、根据分数与除法的关系,两个数的比也可以写成分数形式。
6、比和除法、分数的联系:比前项比号“:”后项比值除法被除数除号“÷”除数商分母分数值分数分子分数线“—”7、比和除法、分数的区别:除法是一种运算,分数是一个数,比表示两个数的关系。
8、根据比与除法、分数的关系,可以理解比的后项不能为0。
体育比赛中出现两队的分是2:0等,这只是一种记分的形式,不表示两个数相除的关系。
(二)、比的基本性质1、根据比、除法、分数的关系:商不变的性质:被除数和除数同时乘或除以相同的数(0除外),商不变。
分数的基本性质:分数的分子和分母同时乘或除以相同的数时(0除外),分数值不变。
比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、最简整数比:比的前项和后项都是整数,并且是互质数,这样的比就是最简整数比。
3、根据比的基本性质,可以把比化成最简单的整数比。
4.化简比:(2)用求比值的方法。
注意:最后结果要写成比的形式。
如:15∶10 = 15÷10 = 3/2 = 3∶25.按比例分配:把一个数量按照一定的比来进行分配。
这种方法通常叫做按比例分配。
如:已知两个量之比为,则设这两个量分别为。
路程一定,速度比和时间比成反比。

第四单元比一、比的意义。
1、比的意义:两个数相除又叫做两个数的比。
2、比的各部分名称。
(1)比号:“:”叫做比号,读作“比”。
(2)比的前项和后项:在两个数的比中,比号前面的数叫做比的前项,比号后面的数叫做比的后项。
(3)比值:比的前项除以后项所得的商,叫做比值。
3、比与分数,除法的关系。
(1)联系:比的前项相当于分数的分子、除法中的被除数;比号相当于分数的分数线、除法中的除号;比的后项相当于分数的分母、除法中的除数;比值相当于分数的分数值、除法中的商。
(2)区别:比表示两个量的倍数关系,分数是一个数,除法是一种运算。
二、比的基本性质。
1、比的基本性质:比的前项和后项同时乘或除以相同的数(0除外),比值不变。
2、化简比:把两个数的比化成最简单的整数比。
(1)整数比的化简方法:比的前项和后项同时除以它们的最大公因数。
(2)分数比的化简方法:比的前项和后项同时乘它们分母的最小公倍数,先转化成整数比,再进行化简;也可以利用求比值的方法化简。
(3)小数比的化简方法:先用恰当的方法转化成整数比,再进行化简。
三、比的应用。
按比例分配问题的解题方法:(1)先求出总份数,再求出各部分量占总量的几分之几,最后求出各部分量。
(2)先求出每份是多少,再用每份数乘各部分量所占的份数,最后求出各部分量。
一、选择题1.(2023秋·江西赣州·六年级统考期末)一条路,已行路程与全部路程之比是3∶7,则已行路程与剩下路程之比是()。
A.3∶7 B.7∶3 C.3∶4 D.4∶32.(2023秋·河南郑州·六年级统考期末)某儿童医院上个月新生男婴儿48名,男、女婴儿人数之比是4∶5。
上月新生女婴儿有()名。
A.108 B.60 C.123.(2023秋·河北保定·六年级校考期末)甲、乙两人从学校走到广场,甲要8分钟,乙要10分钟,甲、乙两人速度的比是()。
A.4∶5 B.5∶4 C.10∶8 D.8∶104.(2022春·浙江绍兴·六年级统考期末)某次数学竞赛中,女生和男生人数的比是3∶4,全体学生的平均成绩是82分,男生的平均成绩是80.5分,女生的平均成绩是()分。