film thickness 化学信息学
- 格式:pdf
- 大小:546.40 KB
- 文档页数:10

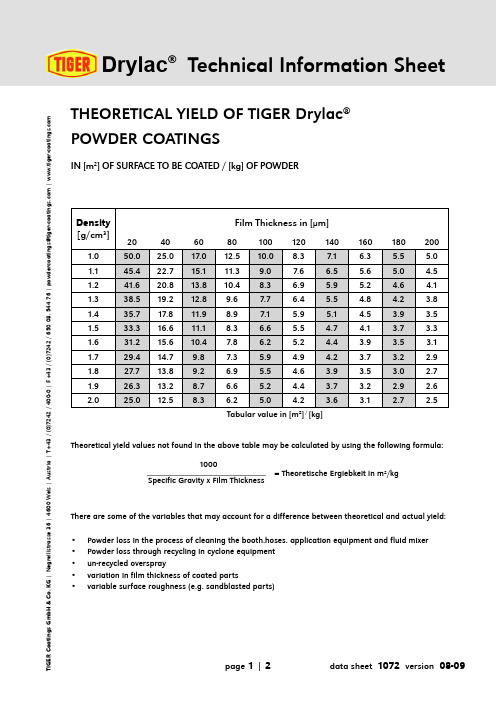
Drylac ®Technical Information SheetR C o a t i n g s G m b H & C o . K G | N e g r e l l i s t r a s s e 36 | 4600 W e l s | A u s t r i a | T +43 / (0)7242 / 400-0 | F +43 / (0)7242 / 650 08. 544 76 | p o w d e r c o a t i n g s @t i g e r -c o a t i n g s .c o m | w w w .t i g e r -c o a t i n g s .c o mTHEORETICAL YIELD OF TIGER Drylac ® POWDER COATINGSIN [m 2] OF SURFACE TO BE COATED / [kg] OF POWDERTheoretical yield values not found in the above table may be calculated by using the following formula:There are some of the variables that may account for a difference between theoretical and actual yield:• Powder loss in the process of cleaning the booth.hoses. application equipment and fluid mixer • Powder loss through recycling in cyclone equipment • un-recycled overspray• variation in film thickness of coated parts•variable surface roughness (e.g. sandblasted parts)1000Specific Gravity x Film Thickness= Theoretische Ergiebkeit in m 2/kgTabular value in [m 2] / [kg]Drylac ®Theoretical YieldR C o a t i n g s G m b H & C o . K G | N e g r e l l i s t r a s s e 36 | 4600 W e l s | A u s t r i a | T +43 / (0)7242 / 400-0 | F +43 / (0)7242 / 650 08. 544 76 | p o w d e r c o a t i n g s @t i g e r -c o a t i n g s .c o m | w w w .t i g e r -c o a t i n g s .c o mTIGER Coatings GmbH & Co. KG Negrellistraße 364600 Wels | Austria T +43 / (0)7242 / 400-0F +43 / (0)7242 / 650 08E powdercoatings@ W certified according toEN ISO 9001 / 14001Our verbal and written recommendations for the use of our products are based upon experience and in accordance with present technological standards. These are given in order to support the buyer or user. They are non-committal and do not create any additional commitments to the purchase agreement. They do not release the buyer from verifying the suitability of our products for the intended application. We warrant that our products are free of flaws and defects to the extent as stipulated in our Terms of Delivery and Payment.As a part of our product information program each of our Product Data Sheets are periodically updated, so that the latest version shall prevail. Therefore, please contact our sales department to make sure that this Product Data Sheet is the most current version. The information in our Product Data Sheets is subject to change without notification.This Product Data Sheet substitutes any and all previous Product Data Sheets and notes for customers published on this subject matter and is only intended to give a general product overview. Please request specific information for products outside of our standard product list (latest version).The Technical Information Sheets and the Terms of Delivery and Payment each in their latest version, available as a download at , form an integral part of this Product Data Sheet.。

第29卷第5期1999年9月 东 南 大 学 学 报JOURNA L OF S OUTHE AST UNI VERSITY Vol 129No 15Sept.1999 T iO 2薄膜厚度及其光学常数的测量王德育 袁春伟(东南大学分子与生物分子电子学实验室,南京210096)摘 要 描述了非线性回归模型在T iO 2薄膜的光学常数及其厚度测量中的应用.利用薄膜在可见光范围内的光谱特性使用曲线拟合技术对它的光学常数进行了测量.研究结果表明,这种方法可以简单、高效地应用于对薄膜厚度及其光学常数的测量.关键词 非线性回归模型;薄膜;光学常数分类号 O433.4 收稿日期:1999-03-01. 第一作者:男,1967年生,博士研究生.干涉测量是常见的测量薄膜厚度及其光学常数的方法之一[1~4].一般说来,如果薄膜具有足够的厚度,则可以方便地测量出薄膜的厚度及其光学常数[5~8],它的根本依据在于标化的透射/反射光谱的相邻的极大或极小点的级数相差1.这种根据极值测量的方法具有一些明显的缺点:①为了在光谱中有足够多的极大或极小值,薄膜必须有足够的厚度,其厚度一般要求在几百nm 以上.所以,这种方法不能用于超薄薄膜的测量;②为了分辨光谱的极大/极小值,基底和干涉层之间必须进行折射率匹配.而往往由于系统噪声的影响,很难直接得到极值对波长的精确定位,从而必须进行多种方法的校正;③对于厚度不均匀的薄膜,不能直接观察到极值.本文通过拟合光谱的以折射率、薄膜厚度及吸光系数为自变量的相对光强的分布函数,利用非线性回归模型同时测定了T iO 2薄膜的多项光学常数.本方法隶属于曲线拟合的范畴,同传统的方法相比具有简单实用的特点,可以用于超薄薄膜的研究.1 相对光强的分布函数垂直入射光I 0可以在不同的折射率界面上发生反射和透射.如果薄膜厚度为d ,折射率为n (n +α/λ2),基底折射率为s ,则本底的透射光谱为[9] t s =I 02s s 2+1(1)当薄膜在基底沉积之后,其透射光谱为[9] t =I 0Ax B -Cx +Dx2(2)式中,A =16sn 2;B =(n +1)3(n +s 2);C =2(n 2-1)(n 2-s 2)cos φ,φ=4πnd/λ;D =(n -1)3(n -s )2;x =exp (8-kλ2)d .为了消除入射光谱和基底的影响,对t s 校正,其相对光强表达式为 t/t s =(n ,s ,d ,λ,k )(3)此相对光强是以薄膜的折射率、厚度和吸光系数为函数的,从而可以以此函数为基础进行薄膜光学特性的研究.非线性回归的拟合过程可概括为2个主要的步骤.第1步,使用所有的初始化值组合进行计算,具有最小均方根(Root 2Mean 2Square ,RMS )的组合被选定进行迭代计算.第2步,通过迭代计算测量光谱与理论光谱间的误差最小,其目的可用式(4)来表示: δT =1j ∑j i =1[T (λi )calc -T (λi )means ]21/2(4)式中,T (λi )calc 为拟合的光谱;T (λi )means 为相对应的测量光谱;j 为每一光谱的采样次数.利用此函数做为非线性拟合的模型.2 数值模拟表1 不同方法对α-Si :H 膜模型的测量结果比较理论值Envelope 曲线拟合95%可信限厚度/μm11.00811,1吸光系数/fm -11.51.521.51.5,1.5折射率n 2.62.5952.6002.599,2.601折射率系数a/μm 20.30.3030.30.3,0.3 为了检验本方法的有效性,引用了参考文献[6]中的模型和数据.从表1给出的结果看出,在没有系统噪声的影响下,曲线拟合技术可以十分精确地测定薄膜的厚度及各项光学常数,并且其厚度结果不受色散的影响,测量的结果同理论值完全一致.为了检验系统噪声对测量结果的影响,在模型中引入了Poisson 分布的系统噪声[10].限定检测极限的定义为:在统计学一类误差的概率p <0105的前提下测量的结果同给定值误差小于10%.系统噪声水平与薄膜厚度的检测极限的关系见图1,两者呈线性关系.模拟结果指出,在一定噪声水平下,随着薄膜厚度的增加,理论值和测量值间的差别越来越小.同时,给出的95%可信限范围也更小.当系统信噪比达到98dB 时,薄膜检测极限为11132nm.图1 系统噪声水平与检测极限的关系3 实 验抛光的玻璃彻底清洗后氮气风干备用.用真空溅射法在载波片表面涂布TiO 2薄膜.透射光谱的测量使用分光光度计(岛津UV 2001,K yoto ,Japan ).光谱波长记录范围在λ=400~800nm 之间.扫描损失忽略不记.光谱数据的分析使用统计分析系统(SAS T M release 6112,SAS Institute Inc ,Cary ,NC ,USA.)中的非线性回归模块,迭代选用了高斯牛顿法,显著性水平定义为0105[11,12].为了得到最小RMS ,选定了多种初始参数组合进行运算.使用台阶仪标定薄膜的厚度做对照.4 结果和讨论利用公式(2),通过测量无干涉层的玻璃基底而折算出基底的色散折射率.其Cauchy 常数和消光常数分别为a =11497640μm 2,b =43311841648nm 2和α=01031fm -1.TiO 2在玻璃基底沉积的透射光谱见图2.从透射光谱曲线可以看出,在扫描光谱范围内没有产生极大或极小601东南大学学报第29卷值,采用非线性模型计算结果表明,其厚度分别为55,90,94和96nm ,其色散折射率为1.8572+4751nm 2/λ2,吸光系数为1131fm -1,同已知的光学常数结果相比[6],具有较好的一致性.在图2和表2中比较了台阶仪标定的薄膜厚度与基于透射光谱的比较,结果显示了较好的一致性.图2 4个T iO 2薄膜样品的透射光谱同依赖于极大或极小值的计算方法相比,光谱拟合的方法具有更高的精度.在表1中,我们比较了同一种假设薄膜的2种不同方法的测量结果.不考虑系统噪声的影响,“envelope ”法在测定的薄膜的厚度上存在“色散”,其最终结果依赖于对各“包络”点膜厚的最终的平均,并且需要借助于经验对一些结果进行必要的取舍.其最终的误差为018%.在没有系统噪声影响的理想状态下,基于回归模型的测量精度为100%.同时,由于非线性拟合方法不依赖于透射光谱的极大极小点,所以可以测定超薄膜的光学特性.表2 基于不同方法测定的T iO 2薄膜厚度样品序号台阶仪测定厚度/nm 光谱仪测定厚度/nm 95%可信限/nm RMS 16154.8554.66 55.056.43×10-828689.9689.58 90.346.41×10-839195.6595.65 96.326.37×10-8 全光谱拟合的可以测定的极限完全依赖于系统的信噪比.所使用的分光光度计中,较为可靠的检测极限为11132nm (98dB ).虽然薄膜光学常数的测量也可以通过其它的一些光谱拟合方法进行[13,14],但是,在这些方法中,为了消除折射率色散的影响,通常只对某特定波长的光谱数据进行拟合,其结果必然出现多个结果.为了排除这个影响,必须对薄膜在不同的角度进行重复多次的测量.基于非线性回归模型的方法,则完全利用采集到的全光谱信息,通过一次迭代计算得到包括Cauchy 折射率常数、吸光系数、薄膜厚度等在内的多项薄膜参数.由于结果的决定取决于最小RMS ,所以不会出现多解的问题,不需要对薄膜进行多次测量.同以往的方法相比,本方法的另一个优点在于吸收系数的测量是直接从光谱数据计算的,选取的计算数据没有光谱区域的限制.相反,现有的方法一般采用从无吸收区测量的结果外推吸收区的方法测量光学常数[7].应用这种方法存在着极其严格的前提条件,即吸收系数与波长之间必须存在着单一的函数关系.这一条件限制了“envelop ”法的广泛的应用.而非线性拟合方法是完全依赖于光谱的测量技术,对于吸收系数与波长的特殊关系,可以采用分段拟合技术进行计算.使用本方法需要注意以下几点:①相对准确的初始值可以极大地减少迭代运算的次数从而提高测量效率;②应该强调,对于统计学的结论,并不完全等同于专业的结论.所以,基于可信限的统计学的结论不仅合理而且十分有用,特别是对于结果的比较,而最终的结论应该是基于测量的结果和专业知识的解释;③一次可以计算的薄膜参数的数量取决于光谱的分701第5期王德育等:T iO 2薄膜厚度及其光学常数的测量801东南大学学报第29卷辨率.较高的光谱分辨率可以同时进行较多参数的测量.5 小 结本文阐述了非线性回归方法在薄膜光学常数测量中的应用.这种方法利用单一入射角度的白光光谱,通过一次计算,可以准确地计算多项薄膜参数,包括厚度、色散折射率、吸收系数等,所有的参数都排除了其它因素的混杂作用.本方法不仅在测量精度上有了提高,同时还克服了传统方法在不同波长下薄膜厚度测量结果不完全一致的现象.这种方法可以用于多种状态下薄膜光学常数及薄膜厚度的测量.参考文献1 Eugene H,Alfred Z.Optics.New Y ork:Addis on2Wesley,1985.277~3082 Max Born,Emil W olt.Principles of optics.Berlin:Pergam on,1990.512~5203 Lin Y,M otesharei K,Dancil S,et al.A porous silicon2based optical interferometric bilsens or.Science,1997,278(31):840~8434 G auglitz G,Brecht A,K raus G.Chemical and biochemical sens ors based on interferometry at him(multi2)layers.Sen2 s ors and Actuators B,1993(11):21~275 S wanepoel R.Determination of the thickness and optical constants of am orphous silicon.J Phys E Sci Instrum,1983, 16(6):1214~12226 Chiao C,Bovard G,Macleod A.Optical2constant calculation over an extended spectral region:application to titanium dioxide film.Applied Optics,1995,34(31):7355~73607 C orales C,Ramirez2Maol B,Fernandez2Pena P,et al.Determining the refractive index and average thickness of AsSe semiconducting glass films from wavelength measurements only.Applied Optics,1995,34(34):7907~79138 Heavens S.Optical properties of thin s olid films.New Y ork:D over,1991.1~979 G oodman F.S tatistical optics.New Y ork:Academic Press,1985.19910Watts G.Estimating parameters in nonlinear rate equations.The Canagian Journal of Chemical Engineering,1994,72(8):701~71011 D obrow olski J,H o C,Waldorf A.Determination of optical constants of thin film coating materials base on inverse syn2 thesis.Applied Optics,1983,22(20):3191~3200Determination of the Thickness andOptical Constants of TiO2FilmWang Deyu Y uan Chunwei(National Laboratory of M olecular and Biom olecular E lectronics,S outheast University,Nanjing210096) Abstract: In this paper,a nonlinear regression m odel is utilized to measure the optical constants ofT iO2thin film.We measured the optical constants by fitting the visible transmission spectra.The results suggest that this method can be applied to estimate optical constants,such as dispersion refractive index, thickness and abs orption coefficient effectively for its versatility.K ey w ords: nonlinear regression m odel;thin film;optical constant。



visual test色彩測定colour measurement膜厚測定film thickness measurement顕微鏡断面厚さ測定法measuring method of coating thickness by microscopical examination of電解式厚さ測定法coulometric method for measuring thickness渦電流式厚さ測定法eddy current method for measuring thickness磁力式厚さ測定法magnetic method for measuring thickness蛍光X線式厚さ測定法X-ray spectrometric method for measureing thicknessβ線式厚さ測定法bata back-scatter method fore measuring thickness測微計厚さ測定法thickness test of coating by micrometer質量計測によるめっき付着量測定法coating weight measurement by gravimetric method滴下法dropping test密着性adhesion密着性試験adhesion test陰極電解式試験cathode electrolysis method for adhesion test押出し試験push out testけい線試験ruled line method for adhesion test研削試験grinding method for adhesion testたがね打込試験chisel drive in testと石試験wetstone testやすり試験file test,file adhesion test熱試験heat test加熱試験heat method for adhesion test熱衝撃試験thermal shock testヒートサイクルテストthermo cycle testバレル試験barrel test 顕微鏡を用皮膜の垂直特定の電解を求める試験。
保留时间retention time被分离样品组分从进样开始到柱后出现该组分浓度极大值时的时间,也既从进样开始到出现某组分色谱峰的顶点时为止所经历的时间,称为此组分的保留时间,用tR表示,常以分(min)为时间单位。
保留时间是由色谱过程中的热力学因素所决定,在一定的色谱操作条件下,任何一种物质都有一确定的保留时间,可作为定性的依据。
半峰宽peak width at half-height又称半宽度、半峰宽度、区域宽度、区域半宽度,是色谱峰高一半处的峰宽度,用y1/2(或W1/2)表示。
半峰宽与标准偏差的关系为:倍频overtune基频以外的其他振动能级跃迁产生的红外吸收频率统称为倍频。
v=0至v=2的跃迁称为第一个倍频2ν,相应地3ν, 4ν……等均称为倍频。
表面增强拉曼Surface-Enhanced Raman Scattering简称SERS。
用通常的拉曼光谱法测定吸附在胶质金属颗粒如银、金或铜表面的样品,或吸附在这些金属片的粗糙表面上的样品。
尽管原因尚不明朗,人们发现被吸附的样品其拉曼光谱的强度可提高103-106倍。
主要用于吸附物种的状态解析等。
薄膜法thin film method适用于高分子化合物的红外光谱测定。
将样品溶于挥发性溶剂后倒在洁净的玻璃板上,在减压干燥器中使溶剂挥发后形成薄膜,固定后进行测定。
差示分光光度法differential spectrophotometry分光光度法中,样品中被测组分浓度过大或浓度过小(吸光度过高或过低)时,测量误差均较大。
为克服这种缺点而改用浓度比样品稍低或稍高的标准溶液代替试剂空白来调节仪器的100%透光率(对浓溶液)或0%透光率(对稀溶液)以提高分光光度法精密度、准确度和灵敏度的方法,称为差示分光光度法。
差示分光光度法又可分高吸光度差示法,低吸光度差示法,精密差示分光光度法等。
超临界流体色谱supercritical fluid chromatography, SFC以超临界流体作流动相,以固体吸附剂(如硅胶)或键合在载体(或毛细管壁)上的有机高分子聚合物作固定相的色谱方法。
TiO2覆膜层厚度的拉曼光谱测定李耿;刘燕【摘要】Titanium dioxide (TiO2 ) is often used as the film material covered on the bottom material .In order to measure the layer thickness of TiO2 coating , the vertical direction of Raman spectra of one‐dimensional mapping technology is used .The data are calculated according to the intensity of rutile A1 g vibration ,located at the 610 cm-1 .The result shows that the thickness of rutile film is 25 μm ,which indicates the Raman mapping is a nondestructive method for measuring film thichness .%为解决T iO2覆膜层厚度值测定和验证问题,采用拉曼光谱一维线扫描技术,对金红石型T iO2覆膜的厚度和物相进行了测定。
研究表明,通过金红石型T iO2位于610 cm-1处的峰A1 g振动的拉曼谱峰强度信息,无损测得了微米级金红石型T iO2覆膜的厚度。
【期刊名称】《实验技术与管理》【年(卷),期】2015(000)010【总页数】3页(P49-51)【关键词】金红石型二氧化钛;覆膜厚度;拉曼光谱扫描【作者】李耿;刘燕【作者单位】中国地质大学北京珠宝学院,北京100083;北京高等珠宝研修学院,北京 100013【正文语种】中文【中图分类】O484.5合成TiO2薄膜材料具有广泛的用途,并常覆于衬底材料上[1-4]。
地铁15号线制动控制箱体及安装支架喷底漆工艺TECHNICAL DATE SHEET技术参数表1. GENERAL INFORMATION一般参数PRODUCT NAME 产品名称:2K-EP-METALLGRUND,CHROMATFREI,AIRLESS 双组分环氧金属底漆,无铬酸盐。
PRODUCT CODE产品代码:SG 64-1002/3COLOUR颜色:BEIGE RED RAL 3012 / 米黄色GLOSS光泽:MAT / 哑光HARDENER固化剂:EH 23-0000/0MIXING RATIO (WEIGHT)混合比例(重量比):5 :1MIXING RATIO (VOLUE)混合比例(体积比):3 : 1POT LIFE存罐时间:6 - 8 h (20 ºC)RAW MATERIAL BASE基础材料:EPPOXIDE RESIN / 环氧树脂THINNER稀释剂:DV20-2183/0APPLICATION 用途:ZINK-PHOSPHAT-RUST PROTECTION-PRIMER FOR INDUSTRIAL GOODS AND VEHICLES.IS SUITABLE AS FINISH-COATING AT A FILMTHICKNESS UP TO 20μm .THE SYSTEM IS SUITABLE FOR ALL ATMOSHPERIC IMPACTS AS WELL AS STRONG CHEMICAL AND STRONG HUMIDITY IMPACTS.磷酸锌防锈底漆,适用于工业产品及交通车辆。
如果膜厚大于20微米也可单独作为面漆使用。
适合于大多数气候条件,耐化学品,耐湿。
2. TECHNICAL INFORMATION技术参数MOTHER LACQUER原漆地铁15号线制动控制箱体及安装支架喷底漆工艺DELIVERY VISCOSITY供货粘度:thixotropic / 触变性SOLID CONTENTS WEIGHT %重量固含量:approx 69%SOLID CONTENTS VOLUME %体积固含量:approx 48 %DENSITY密度:approx 1.52 g / mlVOC−VALUE有机挥发物含量:approx 472.7 g / lVOC−VALUE PER AREA AND MYM每平米每微米厚时有机挥发物含量:0.98 g / ( qm * μm )MIXTURE WITH HARDENER与固化剂混合后SOLID CONTENTS WEIGHT %重量固含量:approx 66 %SOLID CONTENTS VOLUME %体积固含量:approx 49 %DENSITY密度:approx 1.38 g / mlTHEORETICAL FERTILITY 理论覆盖率:approx 351 qm. μm /kg = 2.84 g/qm. Μm(FOR FURTHER INFORMATION REGARDING THE FERTILITY, PLEASE READ THE APPLICATION INFORMATION.)VOC−VALUE有机挥发物含量:approx 472.2 g / lVOC−VALUE PER AREA AND MYM每平米每微米厚时有机挥发物含量:0.97 g / ( qm * μm )RESISTANT TO TEMPERATUREUP TO / 耐温: 120℃DRYING TIME AT 20 DEGREES CENTIGRAD AND 60 μm FILMTHICKNESS 20ºC 60μm膜厚时的干燥时间DUSTDRY不粘尘时间:2 hTOUCHDRY指触干:4 hRECOATABLE可重涂时间:8 hOVEN DRYING强制干燥:20 Minutes80℃地铁15号线制动控制箱体及安装支架喷底漆工艺STORAGE LIFE 储存时间:12 MONTHS next to ROOM−TEMPERATURE IN ORIGINAL PACKING.原包装,室温下可储存12个月。
ORIGINAL PAPERThe Effect of Load (Pressure)for Quantitative EHL Film ThicknessIvan Krupka •Punit Kumar •Scott Bair •M.M.Khonsari •Martin HartlReceived:2October 2009/Accepted:4December 2009/Published online:19December 2009ÓSpringer Science+Business Media,LLC 2009Abstract New quantitative numerical simulations of the elastohydrodynamic lubrication (EHL)film thickness using realistic pressure and shear-dependent rheology and real-istic compressibility have indicated that the dependence of central film thickness upon Hertz pressure (or load)for the classic Newtonian,slightly compressible solution is merely a lower limit with magnitudes three times as great being possible.Experimental measurements of central film thickness employing Hertz pressures from 1.0to 2.6GPa confirm that for a neat mineral oil,the classical pressure dependence is accurate,while for two gear oils the experimental pressure dependence is much larger.Shear-dependent viscosity is a major factor and compressibility plays a lesser role,while there is evidence that mechanical degradation is also important.New experimental evidence of the enhanced scale sensitivity resulting from shear-thinning has also been obtained.These results for the pressure and scale dependence have dire implicationsfor the usual practice of extrapolation of film thickness from experimental measurements at large scale and low pressure using effective pressure–viscosity coefficients.For machines of small scale and high pressure,the extrapola-tion will sometimes result in substantially overestimated film thicknesses.Keywords Elastohydrodynamic ÁFilm thickness ÁEHL ÁRheology ÁCompressibilityList of Symbols B Doolittle parameter b Hertzian contact radius,m a *Redness-greenness coordinate a V Thermal expansivity,K -1E 0Reduced Young’s modulus of two surfaces,Pa f i i th areal fraction F Contact load,N ^G Dimensionless material parameter G i i th shear modulus,Pa h Film thickness,m h c Central film thickness,m H Dimensionless film thickness H =hR x /b 2K Isothermal bulk modulus,Pa K 0Isothermal bulk modulus at p =0,Pa K 00Isothermal bulk modulus at p =0,T =0K,Pa K 00Pressure rate of change of isothermal bulkmodulus at p =0L *Psychometric lightness coordinate M Molecular weight,kg/kmol N Number of flow units n i i th power-law exponent P Pressure,Pa P H Hertz (maximum)pressure,PaI.Krupka ÁM.HartlInstitute of Machine and Industrial Design,Faculty of Mechanical Engineering,Brno University of Technology,Brno 61669,Czech RepublicP.KumarNational Institute of Technology Kurukshetra,Kurukshetra,Haryana 136119,IndiaS.Bair (&)Georgia Institute of Technology,Center for High-Pressure Rheology,George W.Woodruff School of Mechanical Engineering,Atlanta,GA 30332-0405,USA e-mail:scott.bair@M.M.KhonsariDepartment of Mechanical Engineering,Louisiana StateUniversity,2508Patrick Taylor Hall,Baton Rouge,LA 70803,USATribol Lett (2010)37:613–622DOI 10.1007/s11249-009-9559-7R Reduced radius in the rolling direction,ball radius for a ball-on-disk geometry,mR g Universal gas constant=8314.34Pa m3/kmol/K T Temperature,KT R Reference temperature,Ku1,u2Velocities of lower and upper surfaces,respectively;m/sU Dimensionless speed parameter"u Average surface velocity or rolling velocity,m/s V Volume at T and p,m3V R Volume at reference state,T R,p=0,m3V0Volume at p=0,m3V Occupied volume,m3V R Occupied volume at reference state,T R,p=0,m3 ^W Dimensionless load parameterx,X Coordinate in the direction of surface velocity,m, X=x/by,Y Coordinate in the transverse direction,m,Y=y/b z,Z Coordinate along the surface normal to the surface velocity,m,Z=z/ha Reciprocal asymptotic isoviscous pressurecoefficient,Pa-1b K Temperature coefficient of K0,K-1e Occupied volume thermal expansivity,K-1g Rate-dependent shear viscosity,Pa sl Limiting low-shear viscosity,Pa sl0Low-shear viscosity at p=0,Pa sl R Low-shear viscosity at reference state,T R,p=0,Pa sl r Low-shear viscosity at T,p for shear-dependent viscosity measurement,Pa sq Mass density,kg/m3q0Inlet mass density,kg/m3s Shear stress,Pa1IntroductionA new‘‘quantitative approach’’to elastohydrodynamic lubrication(EHL)has emerged recently[1,2]wherein the behavior of the lubricated concentrated contact is calcu-lated using accurate,measurable rheological properties of the liquid.For example,a full generalized Newtonian thermal EHL analysis,including the temperature and pressure dependence of the thermal properties of the liquid, has been obtained[3]for thefilm thickness and friction showing excellent agreement with experiment.This quan-titative approach is superior to the technique of adjusting the viscosity to match simple but inaccurate models to EHL contact behavior.With the quantitative approach,the contribution of each property of the liquid tofilm formation and friction may now be assessed individually;the differ-ent contributions of thermal softening and shear-thinning may be discriminated;differences in performance among liquids of different chemical structure may be understood; and extrapolation of experimental results to very severe contact conditions may be made with improved confidence.A quantitative EHL analysis recently led to an exciting prediction of new EHL behavior from calculation before it was observed experimentally.This involved the sensitivity of the centralfilm thickness,h c,to scale of contact, q(log h c)/q(log R),characterized by the reduced radius, R.The sensitivity of thefilm thickness to scale of contact was shown to be dependent upon the shear dependence of viscosity in the inlet zone[4,5]before this effect was validated by direct measurement[6].New results showing the scale effect are shown in Fig.1a and b for a linear perfluorinated polyalkylether,Z25[7],and a polyglycol gear oil,PG460[8],respectively,for a steel ball rolling against a glassflat.The ball diameter,equal to2R,is given in the legend and other conditions are given in[6].The curves in Fig.1represent the centralfilm thickness cal-culated from the Hamrock and Dowson[9]equation for a slightly compressible Newtonian liquid in circular contact, h c¼1:55a0:53ðl0"uÞ0:67E00:061R0:33pÀ0:201Hð1Þwhich predicts that q(log h c)/q(log R)=0.33.Figure1 clearly reveals that the discrepancy between the Newtonian prediction and the measuredfilm thickness increases as the scale decreases.Specifically,q(log h c)/q(log R)=0.45 and0.48for Z25and PG460,respectively.Similarly,in1996,a simple inlet zone calculation[4] showed that,for an increase in Hertz pressure,p H,from0.5 to1.0GPa,the sensitivity of thefilm thickness to pressure, expressed as D(log h c)/D(log p H)was-0.22for a Newto-nian liquid and-0.46for a Carreau-like liquid with Newtonian limit,G=0.1MPa,and power-law exponent, n=0.5at10m/s and R=1cm.Kudish[5]used a per-turbation analysis to arrive at afilm thickness formula for an Ostwald-deWaele liquid which yieldsh c/pÀ13nþ1Hð2ÞThe prediction is thus h cµp H-0.25for Newtonian and h cµp H-0.4for n=0.5.An Ostwald-deWaele liquid has no Newtonian plateau.Also,a line-contact simulation was performed in preparation for the experimental work pre-sented here.For a shear-thinningfluid in a glass/steel contact with G=0.01MPa and n=0.4,D(log h c)/ D(log p H)was found to be-0.63,much greater than the -0.23of the Newtonian result.Of course,the Hamrock and Dowson Equation1for circular contact gives q(log h c)/q(log p H)=-0.201.This article presents an experimental and analytical investigation of the effect of load on EHLfilm thickness.In a significant departure from previous study,viscosity has not been adjusted to ensure agreement between the two approaches;the viscosities have been measured in visc-ometers known to be accurate.2Experimental LiquidsFour liquids are the subject of thefilm thickness mea-surements and computations reported here.They are a linear perfluorinated polyalkylether,Z25[7];a polyglycol gear oil,PG460[8];a mineral-based,polybutene-thickened gear oil,LF5346,formulated about40years ago for which the viscosity is quite shear-dependent and an abundance of rheological data exists[10];and a mineral oil,SR600, which has been previously employed to assess thefilm dependence on contact load[11].New measurements of low-shear viscosity,l,are reported in this study for SR600 at shear stress of less than70Pa in a falling-body vis-cometer[12],and the results are listed in Table1.Similar data for the Z25and PG460can be found in[12]and for LF5346in[6].Low-shear viscosity data were used to obtain the parameters of the Tait-Doolittle free volume model given in Table2.The equation of state most widely used in high-pressure physics is the empirical Tait equation[12]often held to be the most accurate for extrapolation of volume,V, to very high pressures.VV0¼1À11þK00ln1þpK0ð1þK00Þ!ð3ÞThe ambient pressure bulk modulus may be represented as exponential in temperature.K0¼K00expðÀb K TÞð4Þand a relation between ambient pressure volume and temperature is required.V0V R¼1þa VðTÀT RÞð5ÞThe most widely used model in high-pressure physics for the variation of the low-shear viscosity with temperatureTable1New low-shear viscosity measurementsSR600Temperature/C:40Pressure/MPa0.10.099500.3091000.885200 5.86030031.64001775001250550ThixotropicViscosity in Pa s for SR600Table2The Parameters of the Tait Equation of State(3–5)and the Doolittle Viscosity Equation6 Fluid Doolittle equation parameters Tait equation parametersl R(Pa s)T R(C)B V1RV R K0K00(GPa)b K(K-1)a V(C-1)Z250.36025 5.6800.597611.0150 5.127 6.119910-3 1.0384910-3 PG4600.43740 2.6000.6938119 6.5910-38910-4 LF5346 3.4550 4.3250.666910.8597.428 6.48910-38910-4 SR6000.09940 3.1750.7191119 6.5910-38910-4and pressure has been the free-volume model,using the Doolittle equation.l¼l R exp B V1RV R1VV RÀV1RV RÀ11ÀV1RV R!"#ð6ÞThe viscosity data do not encompass the pressure–viscosity inflection[13]for all materials and,therefore,the Doolittle parameters in Table2should not be unique.In addition, there was no compressibility data available for PG460and SR600to regress the Tait parameters;the‘‘universal’’parameters suggested in[12]were employed instead.The shear stress,s,dependent viscosity,g of Z25was measured in[14],the shear-dependent viscosity of PG460 was measured in[15],and the shear-dependent viscosity of LF5346was measured in[10].Here,the mixture model of reference[16]is employed as the viscosity function.g¼lX Ni¼1f i1þsG i2"#1À1n iðÞ2;X Ni¼1f i¼1ð7ÞThe parameters are listed in Table3.The average molecular weight,M,of the mineral oil, SR600,was estimated from data for a similar paraffinic mineral oil to be520kg/kmol resulting in a Newtonian limit in terms of shear stress using Einstein-Debye[17]of about G=q R g T/M=5MPa.Among EHL lubricants,the shear-thinning response in the inlet zone displayed by SR600and LF5346should represent the low and high extremes,respectively.3EHL Experimental ProcedureFilm thickness measurements were performed using an optical test rig[18].In this apparatus,a circular EHD contact is formed between a transparent disk and a ball. The lower surface of the disk is coated with semi-reflective chromium layer to obtain optimal contrast of chromatic interferograms forfilm thickness evaluation.The contact-ing bodies are enclosed in a thermally isolated,heated chamberfilled with lubricant to ensure fullyflooded con-ditions at constant test temperature,which is checked by a small thermocouple located close to the contact inlet.A halogen lamp is used as a light source,and chromatic interferograms are recorded with a color digital video camera attached to a reflected light microscope.Film thickness values are evaluated from interferograms by thin film colorimetric interferometry[19],which provides lubricantfilm thickness measurement through the colori-metric analysis of chromatic interferograms using an appropriate color matching algorithm and color/film thickness calibration curves.These calibration curves are obtained before each measurement for the specific lubri-cant and contacting bodies.It is believed that thefilm thickness resolution is approximately1nm.The configu-ration of the optical test rig was slightly different for the study of the scale effect and the effect of load(pressure).Results shown in Fig.1were obtained with balls having diameter of5.5,9,25.4,and35mm[6].The root-mean-square surface roughnesses of the balls and the glass disk are about0.005and0.002l m,respectively.Balls having 35and25.4mm in diameter were attached to the shaft driven by servomotor through the planetary gearbox.In this case,the disk was driven by the ball in nominally pure rolling.Balls having9and5.5mm in diameter were sup-ported by four small rolling bearings and were driven by the disk in nominally pure rolling conditions.Film thick-ness experiments were carried out at the loads of1.4,3.8, 30.2,and57N for 5.5-,9-,25.4-and35-mm ball, respectively.The loads correspond to the same maximum contact pressure of518MPa,and the lubricated contact diameters of72,118,334,and458l m for5.5-,9-,25.4-, and35-mm ball,respectively.Lubricant bath temperature was set to25°C for Z25and40°C for PG460.The effect of load(pressure)on centralfilm thickness was studied in a circular EHD contact formed between a sapphire disk and a tungsten carbide(WC)ball of25.4mm in diameter.The disk is115mm in diameter.The root-mean-square surface roughnesses of the ball and disk are about0.006and0.002l m,respectively.The ball is attached to a shaft that is driven by servomotor through a planetary gearbox.The disk is driven by the ball in nom-inally pure rolling.Material properties of the contacting bodies are summarized in Table4.Experimental condi-tions in terms of dimensionless parameters are given in Table5.Lubricant bath temperature was set to40°C for PG460and SR600and50°C for LF5346.Film thickness experiments were carried out at the loads of12,85,and 195N that correspond to the maximum contact pressure of 1029,1977,and2607MPa,respectively.It should be pointed out that material properties of WC ball and sapphire disk given in Table4were obtained from the manufacturers.However,these parameters are used inTable3Parameters for the Mixture Model(7)Liquid Z25PG460LF5346l r(Pa s)102102103N112f1110.96f20.04n10.820.660.6n20.013G1(Pa)7910449105 5.49103 G2(Pa) 1.29107the numerical solution,and it will be shown later that the pressure sensitivity is dependent upon these elastic prop-erties so that the error in their estimation can influence calculations.Therefore,static contact experiments were carried out to check the elastic modulus of the sapphire disk and the WC ball.The constant load of65N was used. Atfirst,the static contact between the glass disk and the WC ball was evaluated.Figure2shows a chromatic interferogram and corresponding cross section providing L*and a*color coordinates across the contact.L*is a psychometric lightness coordinate and a*is a redness-greenness coordinate of the CIELAB uniform color space that is recommended by the Commission Internationale d’Eclairage laboratory for the use in the colorimetric applications.The colorimetric analysis of these color val-ues within chromatic interferogram captured under static contact conditions can be used to evaluate the contact diameter because the Hertzian contact can be recognized as aflat region on the L*and a*curves plotted across the contact.Then,the contact diameter can be used to check the material properties of the WC ball as the modulus of elasticity and Poisson’s ratio of the glass disk is well known.The contact diameter obtained from chromatic interferogram was found to be402.3l m which compares well with value(403.5l m)calculated from data in Table4.Similar comparison was done using the sapphire disk and WC ball(Fig.3)and the measured and calculated contact diameter was263.3l m and262.1l m,respec-tively.Therefore the values given in Table3can be used in this study with confidence.Centralfilm thickness values were obtained from3Dfilm thickness maps evaluated from EHD chromatic interferograms.Figure4shows the com-parison of EHD chromatic interferograms andfilm thick-ness profiles for LF5346captured at rolling speed of 0.0585m/s.4Theoretical AnalysisThe governing equations and the numerical solution scheme are reported in[20].Briefly,the pressure distri-bution is obtained by solving the generalized Reynolds Equation which can be expressed in dimensionless form as follows:Table4Properties of contacting bodiesGlass DiscModulus of elasticity(GPa)81 Poisson’s ratio0.208 Sapphire DiscModulus of elasticity(GPa)420 Poisson’s ratio0.29 Steel ballModulus of elasticity(GPa)210Poisson’s ratio0.3 WC ballModulus of elasticity(GPa)641 Poisson’s ratio0.26Table5Experimental conditionsp H/GPa^U^W^GSR6001.0297.57E-13to4.56E-12 1.35E-07126541.9779.51E-13to4.57E-129.58E-07126542.6079.68E-13to4.95E-12 2.97E-0612654 PG4601.0299.65E-12to1.25E-12 1.35E-0772071.9779.65E-12to1.25E-129.58E-0772072.6079.65E-12to1.25E-12 2.97E-067207 LF53461.0297.62E-11to9.85E-12 1.35E-07131491.9777.62E-11to9.85E-129.58E-07131492.6077.62E-11to9.85E-12 2.97E-0613149(a) L*o o X "q "F 2o P o X þo o Y "q "F 2o P o Y ¼k o o X ð"q H Þþk S 2oo X "q H 1À2"F 1"F 0!ð8Þwhere X ¼x b ,Y ¼y b ,P ¼p p h ,"q ¼q q o,k ¼U E 0p h R b ÀÁ3and S ¼ðu 2Àu 1Þu o is the slide-to-roll ratio with u o representing the average rolling velocity.The present simulations pertain to pure rolling,i.e.,S =0.The integral functions in dimensionless form are:"F0¼Z 11"gd Z ;"F1¼Z 1Z "g d Z and "F 2¼Z 10Z "gZ À"F 1"F 0 d Zð9Þwhere Z =z /h and "g ¼g =l o The pressure distributionobtained numerically satisfies the load balance condition given below in dimensionless form:ZZP d X d Y ¼2p3ð10ÞThe solution domain in the present simulations ranges from X =-4to 1.5,Y =-3to 3discretized using a uniform mesh of 5519601points.It has been verified that thecontacts are fully flooded and any further mesh refinement cause negligible change in the results.5ResultsFilm thickness measurements and calculations are pre-sented for comparison in Figs.5,6,7for LF5346,PG460,and SR600,respectively.The Newtonian solution is seen to be accurate for the neat mineral oil,SR600,at all pressures in Fig.7and for the polyglycol,PG460,at the lowest pressure in Fig.6.As load increases in Fig.6,the mea-sured film thickness becomes progressively less than the Newtonian prediction.That is to say,the Newtonian pre-diction understates the load sensitivity.In Fig.5,the Newtonian prediction is extremely inaccurate for LF5346at all loads,and the load sensitivity is understated.In both Figs.5and 6,the generalized Newtonian solutions offer improvements in the accuracy of prediction of film thickness.It is difficult to compare the pressure sensitivity,q (log h c )/q (log p H ),of experiment and simulation from the plots in Figs.5,6,7.This comparison is made in Table 6where the sensitivities were obtained from a power-law regression of results at the indicated velocities.Clearly,the generalized Newtonian calculation is a major improvement over the classical Newtonian,q (log h c )/q (log p H )&-0.20.However,the magnitude of the pressure sensitivity is understated by the generalized Newtonian calculation as well.6DiscussionThe simulations presented here are quantitative in the sensethat the viscosities used in the calculations were not adjusted to fit experiment or to improve numerical stability;the viscosities were measured in viscometers.Therefore,conclusions generated from the comparisons with experi-ment should provide insight into the real behavior of liquids in the operating contacts.6.1Shear-Dependent ViscosityIn the previous study of the scale effect [6],q (log h c )/q (log R ),the generalized Newtonian calculation also understated the increase of scale effect as a result of shear-thinning for LF5346.In that study,mechanical degradation was advanced as a likely possibility for the increased effect.The same reduction in molecular weight as a result of the imposed shear stress may be responsible here.However,in the course of the viscosity measurements,(a)L*shear stresses of up to 2and 8MPa were applied to PG460and LF5346,respectively,without loss of repeatability.Some insight may be gained from the computed values of shear stress in the inlet.Figure 8shows the evolution of pressure and shear stress along the inlet sweep for two loads.For comparison,x =0has been shifted to the edge of the Hertz boundary.Increasing the load results in increased pressure gradient and shear stress in theimportant region near the Hertz boundary.Since viscosity is reduced by an increase in shear stress when the stress exceeds G 1,the increase in load (contact pressure)must result in a greater decrease in film thickness for the shear-thinning case than for the Newtonian case where viscosity is unaffected by shear.(a)35012 N85 N 195 N 12NN 591N58An additional interesting effect was discovered in the course of the calculations.The load(pressure)effect is dependent upon the elastic modulus of the contacting bodies.Table7summarizes the calculatedfilm thicknesses for different values of E0where conditions have been adjusted to have similar centralfilm thickness.Small val-ues of E0lead to greater load(pressure)sensitivity.This result means that the usual simple power-law form of Eq.1 will not be useful for generalized Newtonian response.The individual exponents may not be independent of the other terms.Clearly,there must be some combination of small scale, R,and high contact pressure,which will result in shear-thinning of even an unformulated low-molecular-weight mineral oil in the inlet zone with the attending departures from classical Newtonianfilm behavior.Table6Pressure sensitivities,q(log h c)/q(log p H),for experiment and analysis for rolling velocity of0.1m/s for PG460and LF5346 and0.2m/s for SR600LF5346PG460SR600Experimental-0.49-0.39-0.21 Analytical-0.31-0.28-0.19The classical Newtonian result is q(log h c)/q(log p H)&-0.20 Table7The pressure effect for variable E0Lubricant E0(GPa)h c/nm(p H=1GPa)h c/nm(p H=2GPa)q(log h c)/q(log p H)Shear-thinning,l o=1Pa.s(G=10kPa,n=0.6)123580433-0.42 Newtonian,l o=0.0978Pa.s123580469-0.30 Shear-thinning,l o=0.79Pa.s(G=10kPa,n=0.6)550580482-0.27 Newtonian,l o=0.0797Pa.s550580494-0.23 Shear-thinning,l o=1Pa.s(G=10kPa,n=0.4)12313189-0.56 Newtonian,l o=0.0118Pa.s123131105-0.32 Shear-thinning,l o=0.715Pa.s(G=10kPa,n=0.4)55013196-0.45 Newtonian,l o=0.0093Pa.s550131108-0.286.2CompressibilityThe compressibility of the liquid further complicates any discussion of the sensitivity of centralfilm thickness to load.Equation19of Venner and Bos[21]can be written ash c¼h incompc Vðp¼p HÞV0ð11Þwhere h c incomp is the centralfilm thickness of an incompressible liquid.Differentiating yieldso h c o p H ¼o h incompco p HVV0p¼p Hþh incompc1V0o Vo pp¼p Hð12Þwhich can be recast aso log h c o log p H ¼h incompch cVV0p¼p Ho log h incompco log p Hþp HVo Vo pp¼p H"#ð13ÞApplication of Eq.11and the definition of bulk modulus K(p)=-V d p/d V giveso log h c o log p H ¼o log h incompco log p HÀp HKðp¼p HÞIn other words,q(log h c)/q(log p H)is the superposition of a component that results from the effect of pressure on geometry,stress and rheology,q(log h c incomp)/q(log p H) with a component resulting from effect of pressure on liquid volume,-p H/K.Differentiation of Eq.3yieldsK¼1À11þK0ln1þpK0ð1þK00Þ!&'½K0þpð1þK00Þð14ÞThe component of q(log h c)/q(log p H)that results from compressibility alone,-p H/K,is listed in Table8for the experimental liquids for which compressibility data are available and for the Tait equation of state with the uni-versal parameters and for the Dowson and Higginson (D&H)equation of state[9]which was used in the simu-lations which resulted in the Hamrock and Dowson Equa-tion1.Clearly,from Table8,a large component(about one-third)of[q(log h c)/q(log p H)]E0,R=const=-0.201for the Hamrock and Dowson Equation1comes from com-pressibility,which is understated by the D&H equation of state except for low pressure and press-ibility increases exponentially with temperature[22].A portion of the discrepancy between the classical prediction of load sensitivity and experiment is therefore a result of compressibility.The glass transition has not been considered above where the equation of state describes liquid-like behavior only. When the viscosity reaches to some very large value of107to 1012Pa s,further liquid-like compression is restricted by the viscosity and a solid-like compressibility governs.7Conclusions1.Quantitative calculations of EHLfilm thickness usingrealistic pressure and shear-dependent rheology and realistic compressibility have indicated that the classical pressure sensitivity,[q(log h c)/q(log p H)]E0,R=const= -0.2,is merely a lower limit with values as great as-0.6 being possible.2.Experimental measurements employing Hertz pressuresfrom1.03to2.6GPa reveal that the pressure sensitivity may be as great as[q(log h c)/q(log p H)]E0,R=const= -0.5.3.The distribution of shear stress along the inlet sweepdepends upon the contact load(pressure).If the viscosity is shear-dependent for the shear stress existing along the inlet,then the viscosity will have a dependence on the load,which differs from the Newtonian case.4.Realistic compressibility accounts for a portion of theenhanced pressure dependence in some cases.5.Mechanical degradation of large lubricant moleculesmay play a part in the pressure sensitivity.5.New experimental evidence of the enhanced scale sensi-tivity resulting from shear-thinning has been obtained. 6.Most published pressure–viscosity coefficients haveresulted from thefitting of a classicalfilm thickness formula to a measurement offilm thickness rather than from a direct measurement of viscosity under pressure.These results have dire implications for the usual practice of extrapolation offilm thickness from experimental measurements at large scale and low pressure using the adjusted pressure–viscosity coeffi-cient.For machines of small scale and high pressure, the extrapolation will sometimes result in substantially overestimatedfilm thickness.Acknowledgments Film thickness measurements were carried out with the support of the Ministry of Education,Youth and Sports of the Czech Republic—Project No.ME09025.Bair was supported by the National Science Foundation under grant number EEC#0540834.Table8The component of q(log h c)/q(log p H)that results from compressibility alone,-p H/KT=20°C T=150°Cp H(GPa)=0.5120.512LF5346-0.084-0.097-0.109-0.100-0.112-0.124 Z25-0.088-0.100-0.112-0.102-0.113-0.125 Universal Tait-0.079-0.093-0.105-0.095-0.107-0.119 D&H-0.075-0.067-0.049-0.075-0.067-0.049。