典型环节及其传递函数

一、实验目的1. 理解并掌握典型环节（比例、惯性、比例微分、比例积分、积分、比例积分微分）的原理及其在控制系统中的应用。

2. 通过实验验证典型环节的阶跃响应特性，分析参数变化对系统性能的影响。

3. 熟悉MATLAB仿真软件的使用，掌握控制系统仿真方法。

二、实验原理控制系统中的典型环节是构成复杂控制系统的基础。

本实验主要研究以下典型环节：1. 比例环节（P）：输出信号与输入信号成比例关系，传递函数为 \( G(s) = K \)。

2. 惯性环节：输出信号滞后于输入信号，传递函数为 \( G(s) = \frac{K}{T s + 1} \)。

3. 比例微分环节（PD）：输出信号是输入信号及其导数的线性组合，传递函数为\( G(s) = K + \frac{K_d}{s} \)。

4. 比例积分环节（PI）：输出信号是输入信号及其积分的线性组合，传递函数为\( G(s) = K + \frac{K_i}{s} \)。

5. 积分环节（I）：输出信号是输入信号的积分，传递函数为 \( G(s) =\frac{K_i}{s} \)。

6. 比例积分微分环节（PID）：输出信号是输入信号、其导数及其积分的线性组合，传递函数为 \( G(s) = K + \frac{K_i}{s} + \frac{K_d}{s^2} \)。

三、实验设备1. 计算机：用于运行MATLAB仿真软件。

2. MATLAB仿真软件：用于控制系统仿真。

四、实验步骤1. 建立模型：根据典型环节的传递函数，在MATLAB中建立相应的传递函数模型。

2. 设置参数：设定各环节的参数值，例如比例系数、惯性时间常数、微分时间常数等。

3. 仿真分析：在MATLAB中运行仿真，观察并记录各环节的阶跃响应曲线。

4. 参数分析：改变各环节的参数值，分析参数变化对系统性能的影响。

五、实验结果与分析1. 比例环节：阶跃响应曲线为一条直线，斜率为比例系数K。

2. 惯性环节：阶跃响应曲线呈指数衰减，衰减速度由惯性时间常数T决定。

典型环节及其传递函数1．比例环节（放大环节）运动方程：，传递函数为：)t (Kr )t (c K )s (G，比例环节的典型例子有运算放大器、齿轮变速箱、电位器、测速发电机等。

2．惯性环节运动方程：)()()(t r t c dtt dc T+，传递函数：0011)(ωω++s Ts s G ，T 10ωT 称为惯性时间常数，只有一个实数极点T 1−，没有零点。

若输入为阶跃函数)()(t ul t r ，则该惯性环节的输出为：()[(0)]t T c t u c u e −=+−，为的初值。

)0(c c 典型的实例有一阶RC 电路。

3．积分环节运动方程：)()(t r dtt dc T 或∫t dt t r T t c 0)(1)(，即环节输出为输入信号的积分，环节由此得名。

传递函数：ss G 1)(积分环节的特点是除非输入信号恒为0，否则积分环节的输出量不可能维持为常数不变。

)(t r )(t c 4．微分环节运动方程：dtt dr Tt c )()(，即环节输出量为输入信号的微分，环节由此得名。

传递函数：，有时Ts s G )(1)(+Ts s G 也称为微分环节。

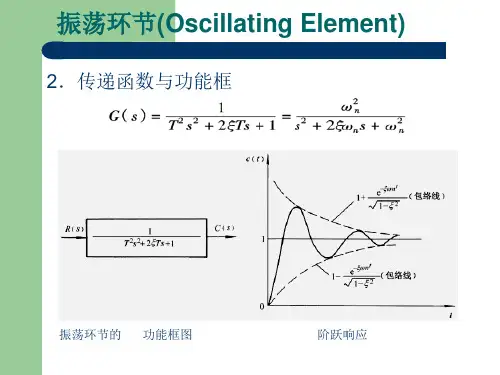
5．振荡环节运动方程：)()()(2)(222t r t c dt t dc T dtt c d T ++ξ传递函数：222222222121121)(nn n s s T T s s T Ts s T s G ωξωωξξ++++++其中T n 1ω，10<≤ξ。

该环节具有一对共轭复数极点，无零点。

其单位阶跃响应呈典型的振荡衰减形式。

6．延时环节运动方程：)()(τ−t r t c ，这个方程实际上不是微分方程而是差分方程。

传递函数：，是的无理函数，函数在s e s G τ−)(s s e τ−∞s 点有无穷多个极点和零点。

====================微分环节不能单独存在只能与其它环节配合使用，。