虚位移原理 第二章(格式整齐)
- 格式:ppt
- 大小:2.49 MB
- 文档页数:9


第十五(1)章 虚位移原理虚位移原理应用功的概念分析系统的平衡问题,是研究静力学平衡问题的另一途径。
虚位移原理与达朗贝尔原理结合起来组成动力学普遍方程,为求解复杂系统的动力学问题提供了另一种普遍的方法,构成了分析力学的基础。
本书只介绍虚位移原理的工程应用,而不按分析力学的体系追求其完整性和严密性。
§15-1 约束·虚位移·虚功1.约束及其分类在第一章,我们将限制物体位移的周围物体称为该物体的约束。
为研究上的方便,现将约束定义为:限制质点或质点系运动的条件称为约束,表示这些限制条件的数学方程称为约束方程。
我们从不同的角度对约束分类如下。
(1)几何约束和运动约束 限制质点或质点系在空间的几何位置的条件称为几何约束。
例如图15-1所示单摆,其中质点M 可绕固定点O 在平面Oxy 内摆动,摆长为l 。
这时摆杆对质点的限制条件是:质点M 必须在以点O 为圆心、以l 为半径的圆周上运动。
若以x ,y 表示质点的坐标,则其约束方程为222l y x =+。
又如,质点M 在图15-2所示固定曲面上运动,那么曲面方程就是质点M 的约束方程,即()0,,=z y x f又例如,在图15-3所示曲柄连杆机构中,连杆AB 所受约束有:点A 只能作以点O 为圆心,以r 为半径的圆周运动;点B 与点A 间的距离始终保持为杆长l ;点B 始终沿滑道作直线运动。
这三个条件以约束方程表示为()()0222222==-+-=+B A B A B A A y l y y x x r y x上述例子中各约束都是限制物体的几何位置,因此都是几何约束。
在力学中,除了几何约束外,还有限制质点系运动情况的运动学条件,称为运动约束。
例如,图5-4所示车轮沿直线轨道作纯滚动时,车轮除了受到限制其轮心A 始终与地面保持距离为r 的几何约束r y A =外,还受到只滚不滑的运动学的限制,即每一瞬时有0=-ϖr v A上述约束就是运动约束,该方程即为约束方程。

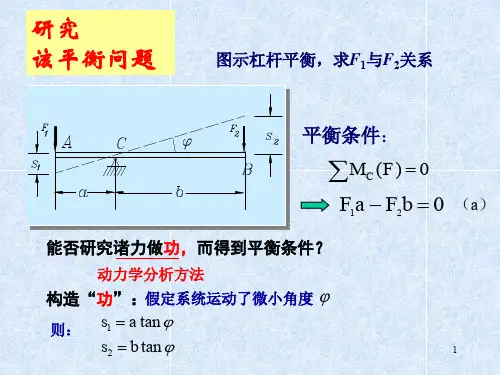
§5、2虚功原理(虚位移原理)一、虚位移和实位移实位移:由于运动而实际发生的位移 dt v r d= 对应时间间隔dt ,同时满足运动微分方程虚位移:t 时刻,质点在约束允许情况下可能发生的无限小位置变更虚位移是可能位移,纯几何概念(非运动学概念),以i rδ表示(1)特点(本质):想象中可能发生的位移,它只取决于质点在t 时刻的位置和约束方程,并不对应一段时间间隔()0=t δ,它是一个抽象的等时变分概念(2)直观意义(求法):对于非稳定约束,在t 时刻将约束“冻结”,然后考察在约束允许情况下的可能位移,即视约束方程中的t 不变()0=t δ,对约束方程进行等时变分运算(同微分运算,注意)0=t δ即可得虚位移;对于稳定约束,由于约束方程中不显含t ,“冻结”已无实际意义,等时变分运算与微分运算完全相同。
Example 质点被限制在以等速u 匀速上升的水平面内运动,约束方程为 0=-ut z 0=z δ udt dz =(3)实位移是唯一的,虚位移可若干个;对稳定约束,实位移为若干个虚位移中的某一个;对非稳定约束,实位移与虚位移不一致。
见273p 图5.2-1二、理想约束实功-作用在质点上的力(含约束力i R )在实位移rd中所作的功 dW虚功-作用在质点上的力(含约束力i R )在任意虚位移rδ中所作的功 W δ其中 i R为第i 个质点受的约束力 若∑=⋅ii i r R 0δ体系所受诸约束反力在任意虚位移中所作元功之和等于零⇒理想约束例如 光滑曲面、曲线约束,刚性杆,不可伸长的绳索等刚性杆约束 022112111='+'-=⋅+⋅r f r f r f r f δδδδ (21f f-= 21f f =; 21r r '='δδ 刚性杆约束所允许) 由于引入了虚位移,巧妙的消取了约束反力(优点 亦是缺点)三、虚功原理(分析力学重要原理之一)(受约束力学体系的力学原理之一)体系受k 个几何约束,在主动力和约束力的共同作用下处于平衡状态,则其中每个质点均处于平衡状态,即 0=+i i R F (2,1=i ……)n 0=⋅+⋅ii i i r R r F δδ⇒对系统求和⇒0=⋅+⋅∑∑i i ii i ir R r Fδδ 对于理想约束∑=⋅ii i r R 0δ 则=W δ0=⋅∑i i ir Fδ∑=++ii iz i iy i ixz F y F x F)(δδδ 虚功原理⇒具有理想约束力学体系,其平衡的充要条件是所有主动力在任意虚位移中所作元功之和等于零 (1717 伯努利)说明:1、由=W δ0=⋅∑i i ir Fδ ,只能求出平衡条件,不能求出约束反力,欲求约束反力i R,需用拉格朗日未定乘数法2、运用虚功原理求平衡条件的方法步骤(1)确定系统自由度,选择合适的广义坐标;(2)将i r表示为广义坐标q的函数,并求出i rδ(i i i z y x δδδ,,);(3)由虚功原理列出平衡方程,并令αδq 的系数为零,求出平衡条件。