第六章一阶电路习题解答

电路习题解答第一章 电路模型和电路定律【题1】：由U A B =5V 可得：I AC .=-25A ：U D B =0：U S .=125V 。

【题2】：D 。

【题3】：300；-100。

【题4】：D 。

【题5】：()a i i i =-12；()b u u u =-12；()c ()u u i i R =--S S S ；()d ()i i R u u =--S SS 1。

【题6】：3；-5；-8。

【题7】：D 。

【题8】：P US1=50 W ；P U S 26=- W ；P U S 3=0；P I S 115=- W ；P I S 2 W =-14；P I S 315=- W 。

【题9】：C 。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

【题14】：3123I +⨯=；I =13A 。

【题15】：I 43=A ；I 23=-A ；I 31=-A ；I 54=-A 。

【题16】：I =-7A ；U =-35V ；X 元件吸收的功率为P U I =-=-245W 。

【题17】：由图可得U E B =4V ；流过2 Ω电阻的电流I E B =2A ；由回路ADEBCA 列KVL 得 U I A C =-23；又由节点D 列KCL 得I I C D =-4；由回路CDEC 列KVL 解得；I =3；代入上 式，得U A C =-7V 。

【题18】：P P I I 12122222==；故I I 1222=；I I 12=； ⑴ KCL ：43211-=I I ；I 185=A ；U I I S =-⨯=218511V 或16.V ；或I I 12=-。

⑵ KCL ：43211-=-I I ；I 18=-A ；U S =-24V 。

第二章电阻电路的等效变换【题1】：[解答]I=-+9473A=0.5A；U Ia b.=+=9485V；IU162125=-=a b.A；P=⨯6125.W=7.5W；吸收功率7.5W。

答案及解析115答案第一章电路模型和电路定律【题1】：由U A B 5 V 可得：IA C 2.5 A：U DB 0 ：U S 125. V。

【题2】：D。

【题3】：300；-100。

【题4】：D。

【题5】： a i i 1 i 2 ； b u u1 u2 ； c u u S i i S R S ； d i iS1RSu u S 。

【题6】：3；-5；-8。

【题7】：D。

【题8】：PU S 1 50 W ；P U S 2 6 W ；P U S3 0 ；P I S 1 15 W ；P I S2 14 W ；P I S 3 15 W 。

【题9】：C。

【题10】：3；-3。

【题11】：-5；-13。

【题12】：4（吸收）；25。

【题13】：0.4。

1【题14】：3 I 1 2 3 ；IA 。

3【题15】：I 4 3 A；I 2 3 A；I 3 1A；I 5 4 A。

【题16】：I 7 A；U 35 V；X 元件吸收的功率为P U I 245 W。

【题17】：由图可得U E B 4 V；流过 2 电阻的电流I E B 2 A；由回路ADEBCA 列KVL 得U A C 2 3I ；又由节点 D 列KCL 得I C D 4 I ；由回路CDEC 列KVL 解得；I 3 ；代入上式，得U A C 7 V。

【题18】：P1 P2 2 II212222 ；故I I122；I 1 I 2 ；⑴KCL：43I I ；I 11 12858A；U I 1 I 1 V 或 1.6 V；或I 1 I2 。

S 2 15⑵KCL：43I I ；I1 121 8 A；U S 24V。

第二章电阻电路的等效变换【题1】：[解答]I9 47 3ab 9 4 8.5 V；A =0 .5 A ；U II 1 U 6ab . A ；P 6 1.2 5 W = 7 .5 W ；吸1 252收功率7.5W。

【题2】：[解答]【题3】：[解答] C。

第六章一阶电路——经典分析法（微分方程描述）——运算分析法（代数方程描述）见第十三章一、重点和难点1. 动态电路方程的建立和动态电路初始值的确定；2. 一阶电路时间常数、零输入响应、零状态响应、冲激响应、强制分量、自由分量、稳态分量和暂态分量的概念及求解；3. 求解一阶电路的三要素方法；电路初始条件的概念和确定方法；1.换路定理（换路规则）仅对动态元件（又称储能元件）的部分参数有效。

①电容元件：u C(0-) = u C(0+)；（即：q C(0-) = q C(0+)）；i C(0-) ≠i C(0+)。

②电感元件：i L(0-) = i L(0+)；（即：ΨL(0-) = ΨL(0+)）；u C(0-) ≠u C(0+)。

③电阻元件：u R(0-) ≠u R(0+)；i R(0-) ≠i R(0+)。

因此，又称电容的电压、电感的电流为状态变量。

电容的电流、电感的电压、电阻的电压和电流为非状态变量。

如非状态变量的数值变化前后出现相等的情况则视为一种巧合，并非是一种规则。

2.画t=0+时刻的等效电路画t=0+时刻等效电路的规则：①对电容元件，如u C(0-) = 0，则把电容元件短路；如u C(0-) ≠ 0，则用理想电压源（其数值为u C(0-)）替代电容元件。

②对电感元件，如i L(0-) = 0，则把电感元件开路；如i L(0-) ≠ 0，则用理想电流源（其数值为i L(0-)）替代电感元件。

画t=0+时刻等效电路的应用：一般情况下，求解电路换路后非状态变量的初始值，然后利用三要素法求解非状态变量的过渡过程。

3. 时间常数τ①物理意义：衡量过渡过程快慢的技术指标(即等于一阶微分方程的特征方程的特征根)。

仅取决于电路的结构和元件的参数。

②几何意义：状态变量变化曲线中时间坐标轴上任意一点次切距的长度（即曲线上任意一点，如果以该点的斜率为固定变化率衰减，则经过τ时间后为零值）。

③单位：m(秒)、ms(毫秒)。

第6章一阶动态电路分析6.1 如图6.3所示电路，在开关S断开前已处于稳态，试求开关S断开后瞬间电压u C和电流i C、i1、i2的初始值。

分析先在时的等效电路中求，因为时电路已处于稳态，电路中各处的电流和电压都是常数，电容中的电流，所以这时电容C可看作开路。

然后在时的等效电路中求、和，这时电容C可用电压为的恒压源代替。

解画出时的等效电路，如图6.4（a）所示。

根据分压公式，得时电容两端的电压为：（V）根据换路定理，时电容两端的电压为：（V）在瞬间，电容C可用电压为V的恒压源代替，由此可画出时的等效电路，如图6.4（b）所示。

由于4Ω电阻支路已断开，故时的电流i2为：（A）根据欧姆定律，得时的电流i1为：（A）根据KCL，得时的电流i C为：（A）图6.3 习题6.1的图图6.4 习题6.1解答用图6.2 如图6.5所示电路，在开关S闭合前已处于稳态，试求开关S闭合后瞬间电压u L和电流i L、i1、i2的初始值。

分析先在时的等效电路中求，因为时电路已处于稳态，电路中各处的电流和电压都是常数，电感两端的电压，所以这时电感L可看作短路。

然后在时的等效电路中求、和，这时电感L可用电流为的恒流源代替。

解画出时的等效电路，如图6.6（a）所示。

根据欧姆定律，得时电感中的电流为：（A）根据换路定理，时电感中的电流为：（A）图6.5 习题6.2的图图6.6 习题6.2解答用图在瞬间，电感可用电流为A的恒流源代替，由此可画出时的等效电路，如图6.6（b）所示。

根据欧姆定律，得时电感两端的电压为：（V）根据分流公式，得时的电流i1和i2分别为：（A）6.3 如图6.7所示电路，在开关S闭合前已处于稳态，试求开关S闭合后瞬间电压u C、u L和电流i L、i C、i的初始值。

分析先在时的等效电路中求和，因为时电路已处于稳态，电路中各处的电流和电压都是常数，电容中的电流，电感两端的电压，所以这时电容C可看作开路，电感L可看作短路。

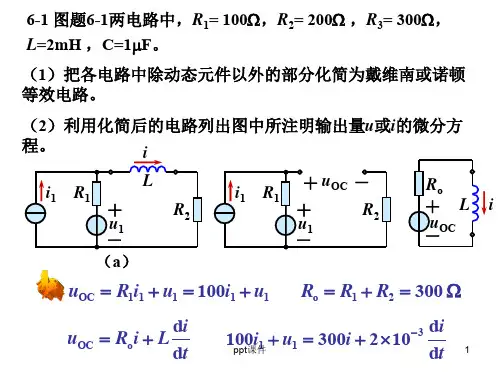
第六章 一阶电路6-1图示各电路中开关S 在0t =时动作，试求各电路在0t +=时刻的电压，电流。

(a)(b)题6-1图2F3ΩΩ3解：(a)在0t <时，电路处于稳固状态，电容看做断路，电路如题解图(a1)所示。

电容上的电压别离为：()1200610363c u V -=⨯=++()220035363c u V -=⨯=++依照换路时电容电压不能跃变，得()()110010c c u u V +-== ()()22005c c u u V +-==画出0+等效电路如题解图(a2)所示。

由图可得结点电压()10n u +为()1111201050363336n u +⎛⎫++=++ ⎪⎝⎭()1013n u V +=故各支路电流为()()112007033n u i A ++-==()()12054063n u i A ++-== ()()13010013n u i A ++-==电阻上得电压为()11307R u i V +=⨯= ()22608R u i V +=⨯= ()33303R u i V +=⨯=(a1)题解6-1图3Ω3Ω－＋3ΩΩ(a2)V(b)中：在0t <时，电路处于稳固状态，电感看做短路，电路如题解图(b1)所示。

依照分流关系有()3200 1.22030L i A -⨯==+由换路定律()()00 1.2L L i i A -+==t +=时等效电路图如题解图(b2)所示。

由图可知()1060R u V += ()2018R u V += ()3036R u V +=()()()2300054L R R u u u V +++=--=-题解6-1图(b1)33A(b2)6-2开关S 原在位置1已久，0t =时合向位置2，求()c u t 和()i t 。

题6-2图解：0t <时的电路如题解6-2图(a)所示。

由图可知()5010*******c u V -=⨯=+故可得电容电压的初始值()()004c c u u V -+==0t >后的电路如题解图(b)所示。

6—1 为什么调幅,检波和混频都必须利用电子器件的非线性特性才能实现？它们之间各有何异同之处? 分析 非线性器件可以产生新的频率分量，而调幅,检波和混频都为了产生新的频率分量.调幅、检波和混频不同点是输入的信号不同，输出的滤波器不同.解 由于调幅、检波和混频均属于频率变换，即输出信号中产生了新的频率分量，而线性器件不可能产生新的频率分量，只有利用非线性器件才能完成频率变换的功能。

调幅、检波和混频三者相同之处是都属于线性频率变换，即实现频谱搬移,它们实现的原理框图都可用下图表示。

非线性器件都可采用乘法器.调幅、检波和混频不同点是输入的信号不同，输出的滤波器不同。

调幅输入的是调制信号()v t Ω和载波()o v t ,即1v =()v t Ω，2v =()o v t ，滤波器是中心频率为载波频率ω0的带通滤波器。

检波输入的是已调制的中频信号()i v t 和本地振荡信号()o v t ,即1v = ()i v t ，2v =()o v t ，滤波器是RC 低通滤波器。

混频输入的是已调制信号vs(t ）和本地振荡信号()o v t ，即1v =()s v t ,2v =()o v t ，滤波器是中心频率为中频频率ωi 的带通滤波器。

6-2 为什么调幅系数m a 不能大于1？ 分析 调幅系数大于1，会产生过量调制。

解 若调幅系数ma>1,调幅波产生过量调制。

如下图所示，该信号传送到接收端经包络检波后使解调出的调制信号产生严重的失真。

6-3 试画下列调幅信号的频谱图，确定信号带宽，并计算在单位电阻上产生的信号功率. (1) )V )(t (102cos )t 32002cos 1.0t 4002cos 2.01(20)t (6⨯π⨯π+⨯π+=v (2） )V (t 102cos t 6280cos 4)t (6⨯π=v分析 根据信号带宽公式和信号功率即可求得.解(1）6()20(10.2cos24000.1cos23200)cos210()()t t t t V υπππ=+⨯+⨯⨯的信号频谱图如下图所示。

电路答案——本资料由张纪光编辑整理（C2-241 内部专用）第一章电路模型和电路定律【题 1】：由UAB 5 V可得： I AC 2.5A： U DB0 ： U S12.5V。

【题 2】： D。

【题 3】： 300； -100 。

【题 4】： D。

【题5】：a i i1i 2；b u u1u2；c u u S i i S R S；d i i S 1R Su u S。

【题 6】： 3；-5 ； -8。

【题 7】： D。

【题 8】：P US150 W ；P US26W；P US30 ； P IS115 W ； P IS214W ；P IS315W。

【题 9】： C。

【题 10】：3； -3 。

【题 11】：-5 ； -13 。

【题 12】：4（吸收）； 25。

【题 13】：0.4 。

【题 14】：31I 2 3； I 1A 。

3【题 15】：I43A； I23A； I31A； I5 4 A。

【题 16】：I7A；U35 V；X元件吸收的功率为 P UI245W。

【题 17】：由图可得U EB 4 V；流过 2电阻的电流 I EB 2 A；由回路ADEBCA列KVL得U AC 2 3I ；又由节点D列KCL得 I CD 4I ；由回路CDEC列KVL解得；I 3 ；代入上式，得 U AC7 V。

【题 18】：P122 I12；故 I 22； I 1I 2；P2I 221I 2⑴ KCL：4I 13I 1；I 18；U S 2I1 1 I 18V或16.V；或I I。

2 5 A512⑵ KCL：4I 13I1；I18A；U S。

224 V第二章电阻电路的等效变换【题 1】：[解答 ]94A = 0.5 A ；U ab9I 4 8.5 V；I73U ab66 125. W = 7.5 W ；吸收I 12 1.25 A；P功率 7.5W。

【题 2】：[解答 ]【题 3】：[解答]C 。

【题 4】： [ 解答 ]等效电路如图所示，I 005. A。

《电路分析基础》第六章一阶电路一阶电路是电路分析中最简单的一种电路，由一个电感或一个电容和一个电压源或电流源组成。

一阶电路是电子工程中非常常见的一种电路，它的特点是响应时间快，稳定性好。

一阶电路主要包括RC电路和RL电路两种类型。

RC电路由一个电阻和一个电容组成，RL电路由一个电阻和一个电感组成。

在分析一阶电路之前，我们首先要了解一些电路的基本概念。

电阻是电路中最基本的元件，用来限制电流的大小。

电容是储存电荷的元件，可以在电路中积累能量，并且具有储能的功能。

电感是储存磁场能量的元件，类似于电容，但储存的是磁场能量。

在一阶电路中，电阻、电容和电感之间存在着不同的关系。

在RC电路中，电压和电流之间的关系是指数关系，电压的变化速度随着时间的增加而减小。

而在RL电路中，电压和电流之间的关系是线性关系，电压的变化速度与时间无关。

一阶电路的分析主要通过微分方程的方法进行。

对于RC电路，我们可以通过二阶微分方程来描述电压和电流的关系，即I(t) = C*dV(t)/dt + V(t)/R。

对于RL电路，我们可以通过一阶微分方程来描述电压和电流的关系，即V(t) = L* dI(t)/dt + I(t)*R。

在分析一阶电路时，我们经常需要查看电路的响应时间和稳定性。

响应时间是指电路在接受输入信号后所需要的时间来达到稳定状态。

稳定性是指当电路处于稳态时，对输入信号的响应是否保持稳定。

对于RC电路和RL电路，我们可以通过解微分方程得到它们的解析解。

对于RC电路，我们可以得到V(t)=V0*(1-e^(-t/RC))的解析解，其中V0是初始电压，R是电阻，C是电容。

对于RL电路，我们可以得到I(t)=I0*(1-e^(-t/RL))的解析解，其中I0是初始电流，R是电阻，L是电感。

通过分析一阶电路的响应时间和稳定性，我们可以更好地理解电路的工作原理，并且可以根据需求来设计出合理的电路。

一阶电路是电子工程中非常重要的一部分，它是电路分析的基础，也是电子产品设计的基础。

6-16.2 图示电路中的开关K 在t =0瞬间闭合，开关闭合之前电容C 上有初始电压10)0(=-C u 伏。

计算t =1ms 和t =4ms 时的电流)(t i 值。

解：开关K 闭合前，0)0(=-C i ，10)0(=-C u V ，根据换路定理 10)0()0(==-+C C u u V ； 换路稳定后 20)(=∞C u V ；时间常数 263101011010--=⨯⨯⨯==RC τs ； 根据三要素法[]τtC C C C eu u u t u -+∞-+∞=)()0()()( t e 1001020--= V ；t t Ce e tu Ct i 10010026101010d d )(---=⨯⨯==mA ； 905.0)10(001.01003==⨯--e i mA ； 67.0)104(001.041003==⨯⨯⨯--e i mA ；6.3 图示电路中的开关K 在t =0瞬间断开，试确定)(t i r 、绘出它的波形图并计算t =2s 和t =6s 时的)(t i r 值。

解：k 打开前， 2)0(=-L i A ；根据换路定理 2)0()0(==-+L L i i A ；2)0()0(-=-=++L r i i A ，换路稳定后 0)()(=∞-=∞r L i i ； 时间常数 122===R L τs ； 根据三要素法[]τtr r r r ei i i t i -+∞-+∞=)()0()()(te e---=-=22τ271.02)2(2-=-=-e i r A ；96.42)6(6-=-=-e i r mA6.4 图示电路中的的A t i )2(2S +⋅=ε，试确定)(t i r 、绘出它的波形图并计算t =2s 和t = 6s 时的)(t i r 值。

（提示：Si 在t = -2s 瞬间被接通）解：S i 动作前， 0)2(=--L i ；根据换路定理 0)2()2(=-=--+L L i i A ；1221)(21)2(=⨯==-+t i i S r A ，换路稳定后 2)(=∞L i A ；0)(=∞r i时间常数 212//21===R R L τs ；根据三要素法[]22)()2()()(+-+∞--+∞=t r r r r ei i i t i )2(5.022+-+-==t t e eA ；)2(-≥t)(s t题2图u C (t)r (t ) Ωr (t )Ω题4图6-2135.0)2()22(5.0==+-e i r A ； 018.0)6()62(5.0==+-e i r A ；6.5 图示电路中的开关K 1在t =0瞬间断开，开关K 2在t =3秒瞬间断开，试确定)(t u C 和)(t i C 并绘出它的波形图。

哈尔滨理工大学电气学院理论电工教研室第六章(一阶电路)习题解答、选择题1 •由于线性电路具有叠加性，所以_C_。

A .电路的全响应与激励成正比；B .响应的暂态分量与激励成正比； C .电路的零状态响应与激励成正比； D .初始值与激励成正比2.动态电路在换路后出现过渡过程的原因是A .储能元件中的能量不能跃变；B .电路的结构或参数发生变化； C .电路有独立电源存在；D .电路中有开关元件存在3.图6—1所示电路中的时间常数为 C 。

哄)对q 片g图6—1.—_ . C1C2—G C2A . (R1 + R2 ) ；B . R^ 1 '；G+C2G +C2C. R2 (C1 + C2)； D . (R1 + R2)(C1 +C2)解：图6—1中G和C2并联的等效电容为G +C2，而将两个电容摘除后，余下一端口电路的戴维南等效电阻为R2，所以此电路的时间常数为R2(G ・c2)。

4 .图6—2所示电路中，换路后时间常数最大的电路是A U.(0 ⑹图6—2解：图6—2(A)、( B)、( C)、( D)所示四个电路中的等效电感L eq分别为L1 L2 2M、哈尔滨理工大学电气学院 理论电工教研室L 2、L - L 2 - 2M 和 L - L 2 2M 。

的电感摘除后所得一端口电路的戴维南等效电阻A . 20 -12e J0t C . 10-12e"t解：由求解一阶电路的三要素法UcC ：) =1O V ，二、填空题t = 0时U ci (O ){ 1 ------------------1 -------- ---------------- '------ *4G4Q2i\1(A )所示电路的时间常数最大。

图6-36U0.5H②tTU cb . adRJb —)S 耳讯U c哈尔滨理工大学电气学院理论电工教研室t》0 时，将图6—2( A)、( B)、( c、( D)中R eq分别为R2、R2、R2和R-i R2。