同底数幂的乘法

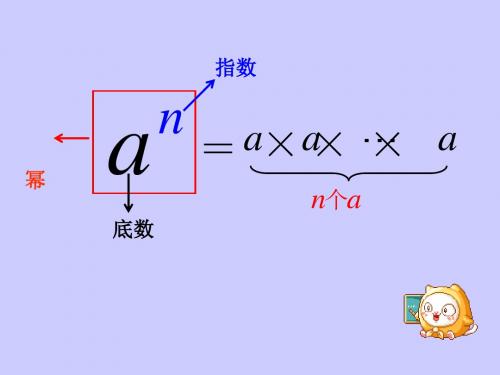
同底数幂的乘法公式首先，我们先明确一些基本概念和符号：- 底数（base）：指数运算中的下标数字，表示要进行乘方运算的数字。

- 幂（exponent）：指数运算中的上标数字，表示底数要进行的乘方运算的次数。

- 乘法（multiplication）：基本数学运算，两个数相乘得到的结果。

a^m*a^n=a^(m+n)其中，a表示底数，m和n表示指数。

这个公式表明，如果两个数的底数相同，那么它们的乘积可以表示为同一个底数的幂，其指数等于两个数的指数之和。

这个公式可以通过以下步骤来证明：假设有两个数a^m和a^n，它们的底数相同，我们可以将它们相乘：a^m*a^n=(a*a*...*a)*(a*a*...*a)其中，a*a*...*a表示连乘m次a，有m个a相乘。

通过乘法的交换律，我们可以重新排列乘积的顺序：a^m*a^n=(a*a*...*a)*(a*a*...*a)=(a*a*...*a*a*a*...*a)两个连乘可以合并成一个连乘，得到：a^m*a^n=a^(m+n)这个证明说明了同底数幂的乘法公式的成立。

举一个例子来说明这个公式的应用：假设有一个数2^3*2^5，根据同底数幂的乘法公式，我们可以将它们相乘并将指数相加：2^3*2^5=2^(3+5)=2^8因此，2^3*2^5=2^8利用同底数幂的乘法公式，我们可以将乘法运算简化为指数运算，从而更容易计算和处理。

-`(a^m)^n=a^(m*n)`：指数的指数等于底数的指数的乘积。

-`a^(-m)=1/(a^m)`：负指数等于底数的倒数的正指数。

-`a^0=1`：任何数的零次方等于1这些性质和公式可以进一步扩展和应用，帮助我们处理更加复杂的指数运算和代数表达式。

总结起来，同底数幂的乘法公式是一个非常有用的数学工具，它可以将乘法运算简化为指数运算，并且可以帮助我们处理复杂的指数表达式。

同底数幂的乘法公式是指当两个数的底数相同时，它们的乘积可以表示为同一个底数的幂，其指数等于两个数的指数之和。

同底数幂相乘的法则
同底数幂是数学术语，它指的是当两个数字的幂都以同一个基数建立时，它们会相乘而不是相加。

这个法则早就被发现，它不仅有助于学生对数学基本概念的理解，同时也有助于开发出有效的解算方法。

这个法则很容易理解，它可以用计算机中的幂表示为：x x m = (x * m)。

样，这个法则也可以用加减乘除的形式表达：x／ m = (x/m) 。

同底数的幂乘法的最重要的优势在于它可以节省计算时间。

如果对两个数进行加减乘除的算术运算，那么就需要一系列步骤，而同底数的幂乘法只需要一步即可完成。

此外，同底数的幂乘法还可以用于看上去很复杂的问题，但只要运用这个法则，就能够很容易和简单地解决它们。

推广开来，同底数的幂乘法也可以用于解决复杂的数学问题，如解决方程，寻找函数的极值，求解多项式的值等等，甚至可以用于实际的工程问题。

由于同底数的幂乘法的优势，它已经被广泛用于科学计算，现代计算机也都采用了这种法则。

它还被应用于金融市场，用来计算未来投资行为的预期回报，通过它可以预测风险和投资收益，也可以用来分析未来股市走势。

同底数的幂乘法应用广泛，它不仅可以用于学校里学生的学习，也可以用于实际工程问题的求解。

它能够节省计算时间和成本，极大地提高计算效率，是一个很重要的数学工具。

综上所述，同底数的幂乘法是一个十分重要的数学工具，可以节
省计算时间和成本，从而极大的提高计算效率。

它可以用来解决学校里的学习问题，也可以用于实际工程等领域问题的解算，是一种值得赞赏的数学工具。

《同底数幂的乘法》教学案例（精选4篇）《同底数幂的乘法》教学案例篇1[课题]义务教育课程标准试验教科书数学（北师大）七班级下册第一章第3节一、教学目的：1、在肯定的情境中，经受探究同底数幂的乘法运算性质的过程，进一步体会幂的意义，进展推理力量和有条理的表达力量。

2、了解同底数幂的乘法运算性质，并能把解决一些简洁的实际问题。

二、教学过程实录：（铃响，上课）老师：在an这个表达式中，a是什么？n是什么？当an作为运算时，又读作什么？同学：a是底数，n是指数，an又读作a的n次幂。

老师：（多媒体投影出示习题）用学过的学问做下面的习题，在做题的过程中，仔细观看，乐观思索，相互讨论，看看能发觉什么。

计算:(1) 22 × 23 (2) 54×53(3) (-3)2 × (-3)2 (4) (2/3)2×(2/3)4(5) (- 1/2)3 × (- 1/2)4 (6) 103×104(7) 2m × 2n (8)(1/7)m×(1/7)n (m,n是正整数)（同学开头做题，相互讨论、争论，气氛热闹，老师巡察、教导，待同学充分争论有所发觉后，提问有何发觉）同学A：依据乘方的意义，可以得到：(1) 22 × 23 = 25(2) 54 × 53 =57(3) (-3)2 × (-3)2 = (-3)5……老师：刚才A同学说出了依据乘方的意义计算上面各题所得结果，计算是否精确？同学：计算精确。

老师：通过刚才的计算和讨论，发觉什么规律性的结论了吗？同学 B：不管底数是什么数，只要底数相同，结果就是指数相加。

老师：请你举例说明。

同学B到前边黑板上板书：22×23=（2×2）×（2×2×2）=2×2×2×2×2=25底数不变，指数2+3=5老师：其他几个题是否也有这样的规律呢？特殊是后两个？同学：都有这样的规律。

同底数幂相乘的法则
同底数幂相乘的法则：同底数幂相乘，底数不变，指数相加。

首先，从法则来看，关键是确定底数是否相同，相同的话，就可以直接进行指数相加。

因此在做同底数幂的乘法时，分析底数是我们必须要做的工作。

底数分析一般有两种情况：第一种情况都是乘法方的形式，底数互为相反数。

在这种情况下，我们需要借助“-1的n次方，对n的奇偶性的判定”来确定整体的一个正负，从而把运算转化成同底数幂的乘法，再借助法则完成计算；第二种情况是底数有乘方关系或者都是某个数的乘方时，我们先把不是乘方形式的数转化成乘方，再判断是不是同底数，最后按照法则进行计算。

无论底数是哪一种情况，我们都需要把能化成同底数的数给化简出来，再进行计算。

其次，法则的逆用。

我们通过同底数幂的乘法法则知道同底数幂的结果的指数是通过求和得来的，那么反过来，我们就可以去求另一个因数的指数。

知道了这些以后，为我们以后解题又提供了一种解题方法。

同底数幂的乘方幂数是指在数学中，对一个数进行连乘运算的次数，也就是指数部分。

而底数则是指乘方运算的基数，也就是底数部分。

本文将详细讨论同底数幂的乘方，并探究其特性和运算规则，以便更好地理解和应用乘方运算。

1. 同底数幂的定义同底数幂指底数相同、指数不同的幂。

比如，对于底数a和指数m、n，a的m次方和a的n次方就是同底数幂。

具体表示为：a^m和a^n。

2. 同底数幂的运算规则同底数幂的运算规则有以下几个重要性质：a. 幂的乘法法则对于同底数的乘方运算，指数相加即可，即a^m * a^n = a^(m+n)。

例如，2^3 * 2^4 = 2^(3+4) = 2^7。

b. 幂的除法法则对于同底数的除法运算，指数相减即可，即a^m / a^n = a^(m-n)。

例如，5^6 / 5^3 = 5^(6-3) = 5^3。

c. 幂的乘方法则对于同底数的乘方运算，底数不变，指数相乘即可，即(a^m)^n =a^(m*n)。

例如，(3^2)^4 = 3^(2*4) = 3^8。

为了更好地理解同底数幂的运算，我们来看一些具体的实例。

a. 例子1：2^4 * 2^5根据乘法法则，我们可以将指数相加，得到2^(4+5) = 2^9 = 512。

因此，2^4 * 2^5 = 512。

b. 例子2：5^7 / 5^4根据除法法则，我们可以将指数相减，得到5^(7-4) = 5^3 = 125。

因此，5^7 / 5^4 = 125。

c. 例子3：(4^3)^2根据乘方法则，我们可以将指数相乘，得到4^(3*2) = 4^6 = 4096。

因此，(4^3)^2 = 4096。

通过以上实例可以发现，同底数幂的乘方运算可以简化为对指数的运算，从而使得复杂的计算变得更加简便。

4. 同底数幂的应用同底数幂在数学和实际生活中有着广泛的应用。

以下是一些常见的应用场景：a. 科学计算在科学领域中，同底数幂的乘方运算是常见的数学操作。

例如，在物理学中，计算物体的能量、功率等都涉及到幂数运算。

同底数幂的乘法典型题同底数幂的乘法是指当底数相同时，指数相加的运算规则。

在数学中，同底数幂的乘法是非常常见的题型，它在代数运算中扮演着重要的角色。

我们来看一个简单的例子：计算2的3次方乘以2的4次方。

根据同底数幂的乘法规则，我们可以将底数相同的幂相加。

所以，2的3次方乘以2的4次方等于2的(3+4)次方，即2的7次方。

通过计算，我们可以得到2的7次方等于128。

这个例子清楚地展示了同底数幂的乘法规则。

同底数幂的乘法也可以用代数式来表示。

如果我们有两个数a和b，并且它们的底数相同，那么a的m次方乘以a的n次方等于a的(m+n)次方。

这个规则可以推广到任意个数的乘法。

例如，a的m 次方乘以a的n次方乘以a的p次方等于a的(m+n+p)次方。

这个规则在解决代数问题时非常有用。

在实际应用中，同底数幂的乘法常常用来简化计算。

例如，在科学计算、工程设计以及金融领域等等，同底数幂的乘法可以帮助我们快速计算复杂的表达式。

通过运用同底数幂的乘法规则，我们可以将复杂的问题转化为简单的乘法运算，提高计算效率。

除了同底数幂的乘法，指数运算还包括同底数幂的除法和幂的幂等运算。

同底数幂的除法是指当底数相同时，指数相减的运算规则。

例如，2的5次方除以2的3次方等于2的(5-3)次方，即2的2次方。

幂的幂等运算是指当进行多次幂运算时，指数相乘的运算规则。

例如，(2的3次方)的4次方等于2的(3*4)次方，即2的12次方。

同底数幂的乘法在数学中有着广泛的应用。

它不仅在代数运算中起到重要作用，还在其他数学分支如几何学、概率论和数论中发挥着重要的作用。

对于学习数学的学生来说，掌握同底数幂的乘法规则是非常重要的基础知识。

总结起来，同底数幂的乘法是指当底数相同时，将指数相加的运算规则。

它在数学中扮演着重要的角色，用于简化计算、解决代数问题以及应用于其他数学分支。

同底数幂的乘法规则可以通过数学表达式来表示，也可以通过具体的例子进行理解。

掌握同底数幂的乘法规则是数学学习中的基础知识，对于提高计算效率和解决实际问题具有重要意义。

人教版同底数幂的乘法同底数幂的乘法是数学中的一个重要概念，常常在代数运算中会遇到。

在人教版的教材中，同底数幂的乘法是初中数学知识的一部分，旨在帮助学生理解指数、幂和乘法运算的关系。

以下是我为你准备的内容：一、同底数幂的概念和性质同底数幂的概念是指具有相同底数的幂，在进行相乘运算时，底数不变，指数相加。

例如，对于底数为a的两个幂a^m和a^n，它们的乘积可以用同底数幂的性质表示为a^m * a^n = a^(m+n)。

这个性质使得我们能够简化复杂的乘法计算，降低运算的难度。

二、同底数幂的乘法计算方法为了更好地理解同底数幂的乘法，我们可以通过具体的计算示例来进行说明。

考虑以下例子：例1：计算2^3 * 2^4。

解：根据同底数幂的乘法性质，我们可以将这两个幂的指数相加，即2^(3+4) = 2^7。

例2：计算10^2 * 10^(-1)。

解：同样地，我们可以将这两个幂的指数相加，即10^(2+(-1)) = 10^1 = 10。

例3：计算3^(-2) * 3^(-3)。

解：同底数幂的乘法性质同样适用于负指数的情况，所以我们可以将这两个幂的指数相加，即3^(-2) * 3^(-3) = 3^(-2-3) = 3^(-5)。

通过这些例子，我们可以看到，在进行同底数幂的乘法运算时，我们只需要将底数保持不变，将指数相加即可得到结果。

三、同底数幂的乘法规律除了上述的同底数幂的乘法性质之外，还有一些其他的规律可以帮助我们更好地理解和运用同底数幂的乘法。

规律1：对于任意非零实数a，a^0 = 1。

这个规律告诉我们，任何非零实数的0次幂都等于1。

例如，2^0 = 1，3^0 = 1，10^0 = 1等等。

规律2：对于任意非零实数a，a^1 = a。

这个规律告诉我们，任何非零实数的1次幂都等于它本身。

例如，2^1 = 2，3^1 = 3，10^1 = 10等等。

规律3：对于任意非零实数a，a^(-n) = (1/a)^n。

同底数幂的乘法运算法则
同底数幂的乘法运算法则是一种有效的数学运算方法，它可以帮助我们快速计算出复杂的数学表达式。

它的基本原理是：如果两个数字的底数相同，那么它们的乘积等于这两个数字的幂相乘。

例如，如果我们要计算2^3 * 2^4，我们可以使用同底数幂的乘法运算法则，将它们转换为2^(3+4)，即2^7，这样就可以得到结果128。

另一个例子是，如果我们要计算3^2 * 3^3，我们可以使用同底数幂的乘法运算法则，将它们转换为3^(2+3)，即3^5，这样就可以得到结果243。

同底数幂的乘法运算法则不仅可以用于计算两个数字的乘积，还可以用于计算多个数字的乘积。

例如，如果我们要计算2^2 * 3^3 * 5^4，我们可以使用同底数幂的乘法运算法则，将它们转换为2^2 * 3^3 * 5^4，即2^(2+3+4) * 3^(2+3+4) * 5^(2+3+4)，这样就可以得到结果2^9 * 3^9 * 5^9，即1953125。

同底数幂的乘法运算法则可以帮助我们快速计算出复杂的数学表达式，而不需要花费大量的时间和精力。

它的使用可以大大提高我们的效率，节省我们的时间和精力，使我们能够更好地利用时间来完成更多的任务。

此外，同底数幂的乘法运算法则还可以帮助我们更好地理解数学原理，更好地掌握数学知识，从而更好地应用数学知识。

总之，同底数幂的乘法运算法则是一种有效的数学运算方法，它可以帮助我们快速计算出复杂的数学表达式，提高我们的效率，节省我们的时间和精力，帮助我们更好地理解数学原理，更好地掌握数学知识，从而更好地应用数学知识。