三角形中点题型

专题22 三角形中位线定理应用问题1．三角形中位线的定义：连接三角形两边中点的线段叫做三角形的中位线。

2．三角形中位线定理：三角形的中位线平行于第三边，并且等于它的一半。

3.对三角形中位线的深刻理解（1）三角形有三条中位线，每一条与第三边都有相应的位置关系与数量关系.（2）三角形的三条中位线把原三角形分成可全等的4个小三角形.因而每个小三角形的周长为原三角形周长的，每个小三角形的面积为原三角形面积的. （3）三角形的中位线不同于三角形的中线.【例题1】（2020•福建）如图，面积为1的等边三角形ABC 中，D ，E ，F 分别是AB ，BC ，CA 的中点，则△DEF 的面积是（ ）A ．1B ．12C ．13D ．14 【答案】D【解析】根据三角形的中位线定理和相似三角形的判定和性质定理即可得到结论．∵D ，E ，F 分别是AB ，BC ，CA 的中点，1214∴DE =12AC ，DF =12BC ，EF =12AB ，∴DF BC =EF AB =DE AC =12，∴△DEF ∽△ABC ，∴S △DEFS △ABC =（DE AC ）2＝（12）2=14， ∵等边三角形ABC 的面积为1，∴△DEF 的面积是14.【对点练习】（2019内蒙古赤峰）如图，菱形ABCD 周长为20，对角线AC 、BD 相交于点O ，E 是CD 的中点，则OE 的长是（ ）A ．2.5B ．3C ．4D ．5【答案】A ．【解析】∵四边形ABCD 为菱形，∴CD ＝BC ＝＝5，且O 为BD 的中点， ∵E 为CD 的中点，∴OE 为△BCD 的中位线，∴OE ＝CB ＝2.5。

【点拨】掌握菱形特点，根据三角形中位线定理解决问题。

【例题2】（2020•临沂）如图，在△ABC 中，D 、E 为边AB 的三等分点，EF ∥DG ∥AC ，H 为AF 与DG 的交点．若AC ＝6，则DH ＝ ．【解析】1．【分析】由三等分点的定义与平行线的性质得出BE ＝DE ＝AD ，BF ＝GF ＝CG ，AH ＝HF ，DH 是△AEF 的中位线，易证△BEF ∽△BAC ，得EF AC =BE AB ，解得EF ＝2，则DH =12EF ＝1． 【解析】∵D 、E 为边AB 的三等分点，EF ∥DG ∥AC ，∴BE ＝DE ＝AD ，BF ＝GF ＝CG ，AH ＝HF ，∴AB ＝3BE ，DH 是△AEF 的中位线，∴DH =12EF ，∵EF ∥AC ，∴△BEF ∽△BAC ，∴EF AC =BE AB ，即EF 6=BE 3BE ，解得：EF ＝2，∴DH =12EF =12×2＝1，【对点练习】（2019广西梧州）如图，已知在△ABC 中，D 、E 分别是AB 、AC 的中点，F 、G 分别是AD 、AE 的中点，且FG ＝2cm ，则BC 的长度是 cm ．【答案】8．【解析】利用三角形中位线定理求得FG＝DE，DE＝BC．如图，∵△ADE中，F、G分别是AD、AE的中点，∴DE＝2FG＝4cm，∵D，E分别是AB，AC的中点，∴DE是△ABC的中位线，∴BC＝2DE＝8cm【点拨】连续两次应用三角形中位线定理处理本题，是关键。

三角形中位线经典测试题1、已知三角形ABC，其中AC与BD交于点O，BC边中点为E，OE=1，求AB的长。

2、已知三角形ABC，其中DE是BC边的中位线，DE=2cm，求BC的长。

3、已知三角形ABC，要测量A、B两点间的距离，取OA的中点C，OB的中点D，测得CD=30米，求AB的长。

4、顺次连结任意四边形各边中点所得到的四边形一定是平行四边形。

5、以三角形的三个顶点及三边中点为顶点的平行四边形共有4个。

6、已知四边形ABCD中，R、P分别是BC、CD上的点，E、F分别是AP、RP的中点，当点P在CD上从C向D移动而点R不动时，线段EF的长不变。

7、已知三角形三边长分别为6、8、10，则它的中位线构成的三角形的面积为24.8、已知△ABC中，AD=11/44AB，AE=AC，BC=16，求DE的长。

9、已知四边形ABCD中，M、N、P、Q分别为AB、BD、CD、AC的中点，证明四边形MNPQ是平行四边形。

10、已知四边形ABCD中，AD∥BC，BC=3AD，E、F分别是对角线AC、BD的中点，证明四边形ADEF是平行四边形。

11、已知四边形ABCD中，AB=CD，E、F分别为BC、AD的中点，BA、EF的延长线交于点M，CD、EF的延长线交于点N，证明∠AME=∠XXX。

12、已知△ABC中，P是中线AD的中点，连接BP并延长交AC于E，F为BE的中点，证明AF∥DE。

13、已知四边形ABCD中，M是OB的中点，连接AM并延长至P，使MP=AM，连接DP交AC于N，证明（1）MN∥AD；（2）S四边形MPNQ=S△XXX。

14、已知△ABC中，AD是外角平分线，CD⊥AD于D，E是BC的中点，证明（1）DE∥AB；（2）DE=1/2(AB+AC)。

15、已知等腰梯形ABCD中，AB∥CD，AB＞CD，AD=BC，对角线相交于点O，∠AOB=60°，且E、F、M分别是OD、OA、BC的中点，证明△EFM是等边三角形。

学生做题前请先回答以下问题问题1：从边与角的角度来考虑直角三角形的性质都有哪些？问题2：遇到斜边上的中点怎么想？问题3：直角三角形斜边上的中线等于__________；如果一个三角形__________________，那么这个三角形是直角三角形．直角三角形性质应用（直角+中点）一、单选题(共7道，每道12分)1.如图，在△ABC中，∠BAC=90°，斜边BC上的高AD=5cm，斜边BC上的中线AE=8cm，那么△ABC的面积为( )A. B.C. D.答案：C解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半2.如图，在Rt△ABC中，CD是斜边AB上的中线，EF过点C且平行于AB．若∠BCF=35°，则∠ACD的度数是( )A.35°B.45°C.55°D.65°答案：C解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半3.如图，在△ABC中，AB=AC=10，BC=8，AD平分∠BAC交BC于点D，点E为AC的中点，连接DE，则△CDE的周长为( )A.20B.14C.13D.10答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半4.如图，∠ABC=∠ADC=90°，E是AC的中点，若∠BCD=75°，则∠BDE=( )A.25°B.20°C.15°D.10°答案：C解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半5.如图，在四边形ABCD中，∠ABC=∠ADC=90°，点E，F分别是对角线AC，BD的中点，则下列结论成立的是( )A. B.C. D.答案：A解题思路：试题难度：三颗星知识点：等腰三角形三线合一性质6.如图，在正方形ABCD和正方形CEFG中，点D在CG上，BC=1，CE=3，H是AF的中点，那么CH的长是( )A.2.5B.C. D.2答案：B解题思路：试题难度：三颗星知识点：直角三角形斜边中线等于斜边一半7.如图，BD，BE是Rt△ABC斜边AC上的中线与高线．已知AB=4，BC=3，则AD:DE:EC等于( )A.5:3:4B.25:9:16C.25:7:18D.3:2:1答案：C解题思路：试题难度：三颗星知识点：等积公式二、填空题(共1道，每道16分)8.如图，在四边形ABCD中，BC⊥AC于点C，BE⊥AD于点E，∠BAC=60°，点G是AB的中点，已知，则GE的长是____．答案：1解题思路：试题难度：知识点：含30°的直角三角形。

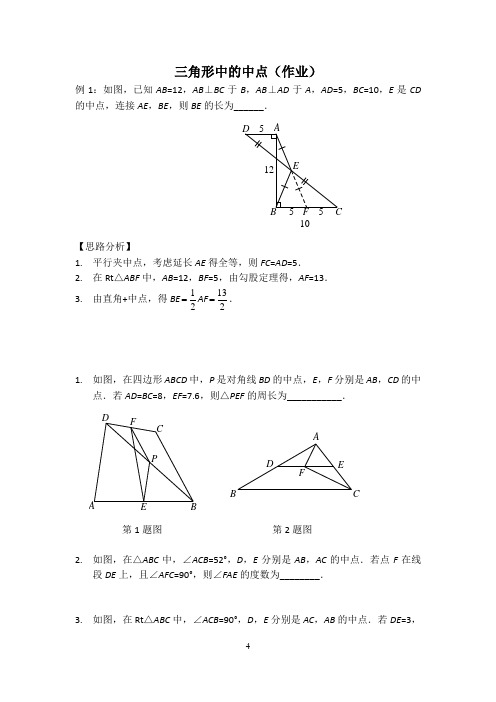
三角形中的中点（作业）例1：如图，已知AB =12，AB ⊥BC 于B ，AB ⊥AD 于A ，AD =5，BC =10，E 是CD 的中点，连接AE ，BE ，则BE 的长为______．1055125F CBED A【思路分析】1.FC =AD =5． 2. 在Rt △ABF 中，AB =12，由勾股定理得，AF =13．3. 由直角+中点，得BE =132．1. 如图，在四边形ABCD 中，P 是对角线BD 的中点，E ，F 分别是AB ，CD 的中点．若AD =BC =8，EF =7.6，则△PEF 的周长为___________．PFDE BCFEDCBA第1题图 第2题图2. 如图，在△ABC 中，∠ACB =52°，D ，E 分别是AB ，AC 的中点．若点F 在线段DE 上，且∠AFC =90°，则∠FAE 的度数为________．3. 如图，在Rt △ABC 中，∠ACB =90°，D ，E 分别是AC ，AB 的中点．若DE =3，CE =5，则AC 的长为___________．4.5. 如图，△ABC 中，AD 是中线，AE 是角平分线，CF ⊥AE 于F ，AB =5，AC =3，则DF 的长为________．FED CBA6.7. 如图，已知AD 为△ABC 的角平分线，AB <AC ，在AC 上截取CE =AB ，M ，N分别为BC ，AE 的中点．求证：∠DAN=∠MNC．【参考答案】1．15.62．64°3．84．3cm5．16．证明略．（提示：连接AF，证明△DBF≌△EAF）7．证明略．（提示：连接BE，取BE的中点F，连接MF，NF）。

三角形中的中点测试（一）（人教版）试卷简介:考查学生几何的有序思考以及模块化思考，检测学生看到中点的多种思考方向。

本次知识方面包括三线合一、倍长中线、类倍长中线、直角三角形斜边中线等于斜边的一半，测试学生辨识类型，对条件的组装和搭配的能力。

一、单选题(共10道，每道10分)1.如图,点E是BC的中点,∠BAE=∠CDE,延长DE到点F使得EF=DE,连接BF.则下列说法:①BF∥CD;②△BFE≌△CDE;③AB=CD;④△ABE为等腰三角形.其中正确的是( )A.①②③B.②③④C.①③④D.①②③④答案：A解题思路：∵E是BC中点，∴BE＝CE，∵∠BEF＝∠CED，EF＝DE，∴△BFE≌△CDE，即②正确；∴∠EBF＝∠C，∠F＝∠CDE，BF＝CD，∴BF∥CD，即①正确；∵∠BAE＝∠CDE，∴∠BAE＝∠F，∴AB＝BF，∴AB＝CD，即③正确；∵无法证明△ABE中两角相等或两边相等，∴△ABE不一定是等腰三角形，即④错误；综上，正确的是①②③．故选A试题难度：三颗星知识点：全等三角形的性质与判定2.如图,在△ABC中,AB=AC,CE是AB边上的中线,延长AB到D,使BD=AB,连接CD.求证:CD=2CE.下列辅助线的作法中,能证明CD=2CE的是( ) ①延长CE到点F,使EF=CE,连接AF.②延长CB到点F,使BF=BC,连接DF.③延长CB到点F,使BF=BC,连接AF.④延长CE到点F,使EF=CE,连接BF.A.①③B.②④C.①④D.②③答案：C解题思路：①结合图中辅助线，可以证明△AEF≌△BEC，∴AF＝BC，∠FAE＝∠CBE，∵AB＝AC，∴∠ABC＝∠ACB，∴∠FAC＝∠FAE+∠BAC＝∠CBE+∠BAC＝∠ACB+∠BAC＝∠CBD，∵AC＝AB＝BD，∴△FAC≌△CBD，∴CD＝CF＝2CE，故①可以；②③不能证明；④结合图中辅助线，可以证明△BEF≌△AEC，∴BF＝AC，∠FBE＝∠A，∵AB＝AC，∴∠ABC＝∠ACB，∴∠FBC＝∠FBE+∠ABC＝∠A+∠ABC＝∠A +∠ACB＝∠CBD，∵AC＝AB＝BD＝BF，BC＝BC，∴△CBF≌△CBD，∴CD＝CF＝2CE，故④可以；综上：①④可以．故选C试题难度：三颗星知识点：全等三角形的性质与判定3.如图,点E是正方形ABCD的边BC的中点,∠BAE=∠FAE,则( )A.AF=FC+AEB.AE=FC+ABC.AE=EC+DFD.AF=FC+AB答案：D解题思路：如图，延长AE交DC的延长线于点G．∵AB∥DG，∴∠BAE＝∠G，∵E是BC的中点，∴BE＝CE，∵∠AEB＝∠GEC，∴△ABE≌△GCE，∴AB＝GC，∵∠BAE＝∠FAE，∴∠G＝∠FAE，∴AF＝FG＝FC+GC＝FC+AB．故选D试题难度：三颗星知识点：类倍长中线4.如图,在△ABD中,C是BD的中点,∠BAC=90°,∠CAD=30°,则( )A.AB=ACB.∠ADB=30°C.AD=2ABD.AD=2AC答案：C解题思路：如图，延长AC至点E，使CE=AC，连接DE．在△ACB和△ECD中∴△ACB≌△ECD∴DE=AB，∠AED=∠BAC=90°∵∠CAD=30°∴AD=2DE即AD=2AB故选C试题难度：三颗星知识点：全等三角形的性质与判定5.如图,在梯形ABCD中,AD∥BC,AB=AD+BC,M是CD的中点。

三角形中点有关的问题[知识引领与方法]1、三角形的中位线①定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半。

②逆定理：在▲ABC 中，M 是 ABC 的边AB 的中点，过点M 作MN ∥BC ，交AC 于点N ，则点N 是边AC 的中点，且BC MN 21 。

2、直角三角形斜边上的中线直角三角形斜边上的中线等于斜边的一半。

[例题精选及训练]类型一、见斜边，想中线例1、如图，在▲ABC 中，若∠B=2∠C ，AD ⊥BC ，E 为BC 边的中点。

求证：AB=2DE 。

【思路提示】取斜边AC 或AB 的中点，利用斜边中线性质和中位线性质。

例2、如图，在Rt ▲ABC 中，∠ACB=90°，点D 、E 分别是AB ，AC 的中点，点F 在BC 的延长线上，且∠CEF=∠A 。

求证：DE=CF 。

【思路提示】点D ，E 分别是直角三角形ABC 斜边和直角边的中点，利用斜边中线的性质和中位线解题。

【变式练习1】如图，在Rt ▲ABC 中，∠ACB=90°，M 是AB 的中点，E ，F 分别是AC ，BC 延长线上的点，且CE=CF=21AB ，则∠EMF 的度数为多少？【变式练习2】如图，在Rt▲ACB中，C为直角顶点，∠ABC=25°，O为斜边中点，将OA绕着点O逆时针旋转θ（0°＜θ＜180°）至OP，当▲BCP恰为轴对称图形时，θ的值为多少？类型二、见多个中点，想中位线例3、如图，已知▲ABC中，AB=AC，CE是AB边上的中线，延长AB到点D，使BD=AB，求证：CD=2CE。

例4、问题一：如图（1），在四边形ABCD中，AB=CD，E，F分别是BC，AD的中点，连接EF 并延长，分别与BA，CD的延长线交于点M，N。

求证：∠BME=∠CNE。

问题二：如图（2），在四边形ADBC中，AB与CD相交于点O，AB=CD，E，F分别是BC，AD的中点，连接EF，分别交DC，AB于点M，N，判断▲OMN的形状，请直接写出结论。

三角形中线练习题三角形中线练习题三角形是几何学中常见的图形之一，它具有丰富的性质和特点。

其中，中线是三角形内部的一条特殊线段，它连接三角形的一个顶点与对边中点。

本文将通过一些练习题来帮助读者更好地理解和应用三角形中线的性质。

练习题一：证明三角形中线相等已知三角形ABC，D、E、F分别为BC、AC、AB的中点。

请证明：AD=BE=CF。

解析：要证明AD=BE=CF，我们可以利用向量的性质来推导。

设向量→AB=a，→AC=b，则→AD=(→AB+→AC)/2=(a+b)/2。

同理，→BE=(→BA+→BC)/2=(b+c)/2，→CF=(→CA+→CB)/2=(c+a)/2。

由于向量的加法满足交换律和结合律，所以有(a+b)/2=(b+c)/2=(c+a)/2，即AD=BE=CF。

因此，三角形中线相等。

练习题二：求三角形中线长度已知三角形ABC，D、E、F分别为BC、AC、AB的中点。

已知AB=6，AC=8，BC=10，求AD、BE、CF的长度。

解析：根据练习题一的证明，我们知道AD=BE=CF。

由于D、E、F分别为BC、AC、AB的中点，所以AD=BC/2=10/2=5，BE=AC/2=8/2=4，CF=AB/2=6/2=3。

因此，AD=5，BE=4，CF=3。

练习题三：证明三角形中线平行已知三角形ABC，D、E、F分别为BC、AC、AB的中点。

请证明：AD∥BE∥CF。

解析：要证明AD∥BE∥CF，我们可以利用向量的性质来推导。

设向量→AB=a，→AC=b，则→AD=(→AB+→AC)/2=(a+b)/2。

同理，→BE=(→BA+→BC)/2=(b+c)/2，→CF=(→CA+→CB)/2=(c+a)/2。

由于向量的加法满足交换律和结合律，所以有(a+b)/2=(b+c)/2=(c+a)/2，即AD∥BE∥CF。

因此，三角形中线平行。

练习题四：求三角形中线的交点坐标已知三角形ABC，D、E、F分别为BC、AC、AB的中点。

三角形的中位线习题归类一、 直接应用1． 如图1所示，EF 是△ABC 的中位线，若BC=8cm ，则EF=_______cm ．2．三角形的三边长分别是3cm ，5cm ，6cm ，则连结三边中点 所围成的三角形的周长是_________cm ．3．在Rt △ABC 中，∠C=90°，AC=•5，•BC=•12，•则连结两条直角 边中点的线段长为_______．4．若三角形的三条中位线长分别为2cm ，3cm ，4cm ，则原三角形的周长为_______．5．如图2所示，A ，B 两点分别位于一个池塘的两端，小聪想用绳子测量A ，B 间的距离，但绳子不够长，一位同学帮他想了一个主意：先在地上取一个可以直接到达A ，B 的点C ，找到AC ，BC 的中点D ，E ，并且测出DE的长为10m ，则A ，B 间的距离为_______．6.已知△ABC 的周长为1，连结△ABC 的三边中点构成第二个三角形， •再连结第二个三角形的三边中点构成第三个三角形，依此类推， 第2010个三角形的周长是（ ）A 、20081B 、20091C 、220081D 、220091 7．如图4,在△ABC 中，E ，D ，F 分别是AB ，BC ，CA 的中点，AB=6， AC=4，则四边形AEDF•的周长是（ ）A ．10B ．20C ．30D ．408.如图所示，□ ABCD 的对角线AC ，BD相交于点O ，AE=EB ，求证：OE ∥BC ．9.如图所示，在△ABC 中，点D 在BC 上且CD=CA ，CF 平分∠ACB ，AE=EB ，求证：EF=12BD ．10.如图所示，已知在□ABCD 中，E ，F 分别是AD ，BC 的中点，求证：MN ∥BC ．11.已知：如图，E 为□ABCD 中DC 边的延长线上的一点，且CE ＝DC ，连结AE 分别交BC 、BD 于点F 、G ，连结AC交BD 于O ，连结OF ．求证：AB ＝2OF ．12.如图，△ABC 中，AD=41AB ，AE=41AC ，BC=16.求DE 的长.(角平分线的垂线必有等腰三角形)13.如图，在△ABC 中，已知AB=6，AC=10，AD 平分∠BAC ，BD ⊥AD 于点D ，E•为BC 中点．求DE 的长．14.如图，AD 是△ABC 的外角平分线，CD ⊥AD 于D ，E 是BC 的中点.求证：（1）DE ∥AB ； （2）DE=21（AB+AC ）如图17，BE 、CF 是△ABC 的角平分线，AN ⊥BE 于N ，AM ⊥CF 于M . 求证：MN ∥BC .B G A E F H D C二、中点寻线，线组形（多个中点）1.如图，在四边形ABCD 中，点E 是线段AD 上的任意一点 ，G F H ，，分别是BE BC CE ，，的中点．证明四边形EGFH 是平行四边形；2.如图，在四边形ABCD 中，AD=BC ，点E ，F ，G 分别是AB ，CD ，AC 的中点。

第七讲全等三角形中点模型模型一：倍长中线或类中线（与中点有关的线段）构造全等三角形模型分析如图①，AD是△ABC的中线，延长AD至点E使DE=AD，易证：△ADC≌△EDB（SAS）。

如图②，D是BC中点，延长FD至点E使DE=FD，易证：△FDB≌△FDC（SAS）。

当遇见中线或者中点的时候，可以尝试倍长中线或类中线，构造全等三角形，目的是对已知条件中的线段进行转移。

例1-1.如图，已知在△ABC中，AD是BC边上的中线，E是AD上一点，连接BE并延长AC 于点F，AF=EF。

求证：AC=BE。

例1-2.如图①，点O为线段MN的中点，PQ与MN相交于点O，且PM∥NQ，可证△PMO≌△QNO．根据上述结论完成下列探究活动：(1)如图②，在四边形ABCD中，AB∥DC，E为BC边的中点，∠BAE＝∠EAF，AF与DC的延长线相交于点F．试探究线段AB与AF、CF之间的数量关系，并证明你的结论；(2)如图③，DE、BC相交于点E，BA交DE于点A，且BE：EC＝1：2，∠BAE＝∠EDF，CF∥AB．若AB＝4，CF＝2，求DF的长度．思考题1.已知：点P是平行四边形ABCD对角线AC所在直线上的一个动点(点P不与点A、C重合)，分别过点A、C向直线BP作垂线，垂足分别为点E，F，点O为AC的中点．(1)当点P与点O重合时如图①，求证OE＝OF；(2)直线BP绕点B逆时针方向旋转，当∠OFE＝30°时，如图②、图③的位置，猜想线段CF、AE、OE 之间有怎样的数量关系？请写出你对图②、图③的猜想，并选择一种情况给予证明．模型二：已知等腰三角形底边中点，可以考虑与顶点连接用“三线合一”模型分析等腰三角形中有底边中点时，常作底边的中线，利用等腰三角形“三线合一”的性质得到角相等或边相等，为解题创造更多的条件，当看见等腰三角形的时候，就应想到：“边等、角等、三线合一”。

例2-1.如图，在△ABC中，AB=AC-5，BC=6，M为BC的中点，MN⊥AC于点N，求MN的长度。