计量经济学学习辅导(庞皓主编)PPT模板
- 格式:pptx
- 大小:1.21 MB
- 文档页数:35




第二章简单线性回归模型第一节回归分析与回归函数P15(一)相关分析与回归分析1、相关关系2、相关系数3、回归分析(二)总体回归函数(条件期望)(三)随机扰动项(四)样本回归函数第二节简单线性回归模型参数的估计P26(一)简单线性回归的基本假定(二)普通最小二乘法求样本回归函数(三)OLS回归线的性质(四)最小二乘估计量的统计性质1、参数估计量的评价标准(无偏性、有效性、一致性)2、OLS估计量的统计特性(线性特性、无偏性、有效性、高斯-马尔可夫定理)第三节拟合优度的度量(RSS、ESS、TSS)P35(一)总变差的分解(二)可决系数(三)可决系数与相关系数的关系第四节回归系数的区间估计与假设检验P38(一)OLS估计的分布性质(二)回归系数的区间估值(三)回归系数的假设检验1、Z检验2、t检验第五节回归模型预测P43第六节案例分析P48第三章多元线性回归模型第一节多元线性回归模型及古典假定P64一、多元线性回归模型二、多元线性回归模型的矩阵形式三、多元线性回归模型的古典假定第二节多元线性回归模型的估计P68一、多元线性回归性参数的最小二乘估计二、参数最小二乘估计的性质(线性特性、无偏性、有效性)三、OLS估计的分布性质四、随机扰动项方差的估计五、多元线性回归模型参数的区间估计第三节多元线性回归模型的检验P74一、拟合优度检验(多重可决系数、修正的可决系数)二、回归方程的显著性检验(F-检验)三、回归参数的显著性检验(t-检验)第四节多元线性回归模型的预测P79第五节案例分析P81第四章多重共线性第一节什么是多重共线性P94第二节多重共线性产生的后果第三节多重共线性的检验第四节多重共线性的补救措施第五节案例分析P109。




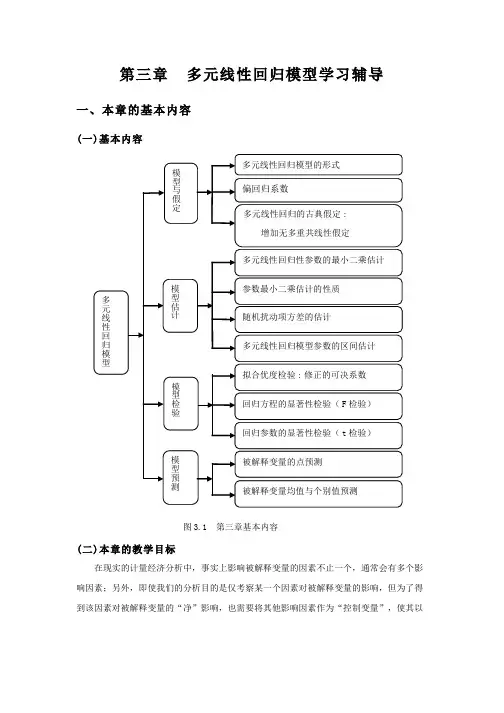
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中,事实上影响被解释变量的因素不止一个,通常会有多个影响因素;另外,即使我们的分析目的是仅考察某一个因素对被解释变量的影响,但为了得到该因素对被解释变量的“净”影响,也需要将其他影响因素作为“控制变量”,使其以显性形式出现在模型中,以提高模型估计精度。
因此,在对现实经济问题进行计量经济分析时,通常需要建立包含两个及两个以上解释变量的计量模型,此类模型称为多元回归模型。
多元回归模型是在简单回归模型理论基础上的扩展,其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致,只是因解释变量增多,从而带来一些新的内容,比如模型整体显著性检验(F 检验)、修正的可决系数(2R )以及解释变量之间多重共线性等问题。
本章的教学目标是:深刻理解建立多元回归模型的目的;掌握多元线性回归模型估计、检验的理论与方法;熟练掌握多元线性回归EViews 输出结果的解释。
二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。
在多元线性回归模型中,解释变量对应的参数是偏回归系数,表达的是控制其他解释变量不变的条件下,该解释变量的单位变动对被解释变量平均值的“净”影响。
为了更深刻理解偏回归系数,可以两个解释变量的多元线性回归模型为例加以说明1。
例如,被解释变量Y 与解释变量2X 和3X 都有关,如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关,可以作回归:1332i i i Y b b X u =++,若用OLS 估计其参数,并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-,这里的2i e 表示除去3i X 影响后的i Y 。

第二章 简单线性回归模型学习辅导一、本章的基本内容(一)基本内容图2.1 第二章的基本内容(二)本章的教学目标在计量经济模型中,只有两个变量且为线性的回归模型是最简单的,称为简单线性回归模型。
简单线性回归模型形式简单,估计和检验的结果表述较为容易,其原理可以直接用代数式和平面坐标图形去直观表述,更容易使初学者理解和接受。
而且先讨论简单线性回归模型,使其对计量经济学的理论和思想有较深刻的认识,然后可以很容易拓展到更一般的多元的情况。
所以,本章从简单线性回归模型入手,讨论计量经济学最基本的理论与方法,为以后各章对计量经济学理论与方法的拓展和深化打下基础。
本章的教学目标是:深刻理解计量经济分析的基本思想;明确估计计量经济模型的基本假定;掌握估计和检验计量经济模型的基本思想和方法;能够运用简单线性回归模型作经济结构分析和经济预测等方面的应用;并要求初步掌握EViews最基本的操作方法。
二、重点与难点分析1. 从条件期望的角度深刻认识回归函数的实质总体回归函数(PRF)是将总体被解释变量Y的条件期望表现为解释变量X的某种函数。
总体回归函数所体现的实际是经济现象或经济变量之间的客观规律性。
由于受种种偶然因素的影响, 经济变量之间的数量规律在经济现象的个别观测值中难以直接观测,只有从变量条件期望的角度才能揭示经济现象数量关系的规律性。
作为经济总体运行的客观规律,总体回归函数是客观存在的,但是在实际的经济研究中总体回归函数通常又是未知的,只能根据经济理论和研究者的实践经验去设定。
在计量经济学研究中,“计量”的根本目的是去揭示客观存在的经济数量规律,也就是要努力寻求总体回归函数。
我们所设定的计量经济模型实际就是在设定总体回归函数的具体形式。
样本回归函数(SRF)是将被解释变量Y的样本条件均值表示为解释变量X的某种函数。
样本回归线会随着抽样波动而变化,每次抽样都能获得一个样本,也就可以拟合出一条样本回归线,所以样本回归函数是不唯一的。