计量经济学庞皓简单线性回归模型

第一章导论第一节什么是计量经济学计量经济学是现代经济学的重要分支。

为了深入学习计量经济学的理论与方法，有必要首先从整体上对计量经济学有一些概略性的认识，了解计量经济学的性质、基本思想、基本研究方法以及若干常用的基本概念。

一、计量经济学的产生与发展在对实际经济问题的研究中，经常需要对经济活动及其数量变动规律作定量的分析。

例如，为了研究中国经济的增长，需要分析中国国内生产总值(GDP)变动的状况? 分析有哪些主要因素会影响中国GDP的增长？分析中国的GDP与各种主要影响因素关系的性质是什么？分析各种因素对中国GDP影响的程度和具体数量规律是什么？分析所得到的数量分析结果的可靠性如何？还要分析经济增长的政策效应，或者预测中国GDP发展的趋势。

显然，对这类经济问题的定量分析，需要解决一些共性问题：提出所研究的经济问题及度量方式，确定表现研究对象的经济变量（如用GDP的变动度量经济的增长）；分析对研究对象变动有影响的主要因素，选择若干作为影响因素的变量；分析各种影响因素与所研究经济现象相互关系的性质，决定相互联系的数学关系式；运用科学的数量分析方法，确定所研究的经济对象与各种影响因素间具体的数量规律；运用统计方法分析和检验所得数量结论的可靠性；运用数量研究的结果作经济分析和预测。

对社会经济问题数量规律的研究具有普遍性，计量经济学是专门研究这类问题的经济学科。

计量经济学（Econometrics）这个词是挪威经济学家、第一届诺贝尔经济学奖获得者弗瑞希（R.Frisch）在其1926年发表的《论纯经济问题》一文中，按照”生物计量学”(Biometrics)一词的结构仿造出来的。

Econometrics一词的本意是指“经济度量”，研究对经济现象和经济关系的计量方法，因此有时也译为“经济计量学”。

将Econometrics译为计量经济学，是为了强调计量经济学是一门经济学科，不仅要研究经济现象的计量方法，而且要研究经济现象发展变化的数量规律。

第一章导论第一节什么是计量经济学计量经济学是现代经济学的重要分支。

为了深入学习计量经济学的理论与方法，有必要首先从整体上对计量经济学有一些概略性的认识，了解计量经济学的性质、基本思想、基本研究方法以及若干常用的基本概念。

一、计量经济学的产生与发展在对实际经济问题的研究中，经常需要对经济活动及其数量变动规律作定量的分析。

例如，为了研究中国经济的增长，需要分析中国国内生产总值(GDP)变动的状况? 分析有哪些主要因素会影响中国GDP的增长？分析中国的GDP与各种主要影响因素关系的性质是什么？分析各种因素对中国GDP影响的程度和具体数量规律是什么？分析所得到的数量分析结果的可靠性如何？还要分析经济增长的政策效应，或者预测中国GDP发展的趋势。

显然，对这类经济问题的定量分析，需要解决一些共性问题：提出所研究的经济问题及度量方式，确定表现研究对象的经济变量（如用GDP的变动度量经济的增长）；分析对研究对象变动有影响的主要因素，选择若干作为影响因素的变量；分析各种影响因素与所研究经济现象相互关系的性质，决定相互联系的数学关系式；运用科学的数量分析方法，确定所研究的经济对象与各种影响因素间具体的数量规律；运用统计方法分析和检验所得数量结论的可靠性；运用数量研究的结果作经济分析和预测。

对社会经济问题数量规律的研究具有普遍性，计量经济学是专门研究这类问题的经济学科。

计量经济学（Econometrics）这个词是挪威经济学家、第一届诺贝尔经济学奖获得者弗瑞希（R.Frisch）在其1926年发表的《论纯经济问题》一文中，按照”生物计量学”(Biometrics)一词的结构仿造出来的。

Econometrics一词的本意是指“经济度量”，研究对经济现象和经济关系的计量方法，因此有时也译为“经济计量学”。

将Econometrics译为计量经济学，是为了强调计量经济学是一门经济学科，不仅要研究经济现象的计量方法，而且要研究经济现象发展变化的数量规律。

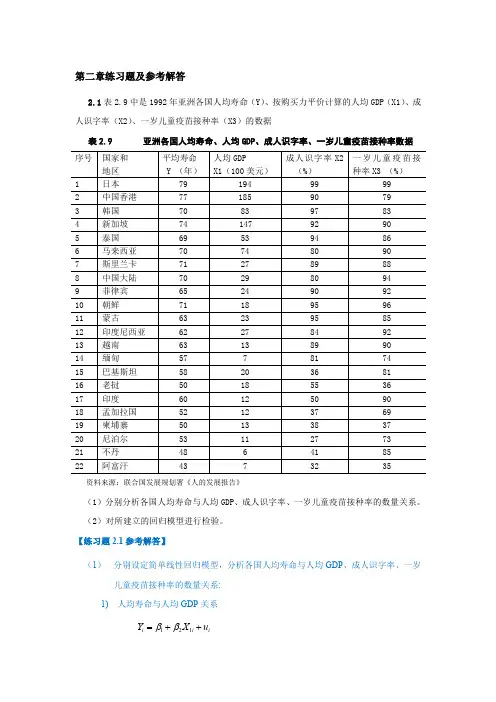
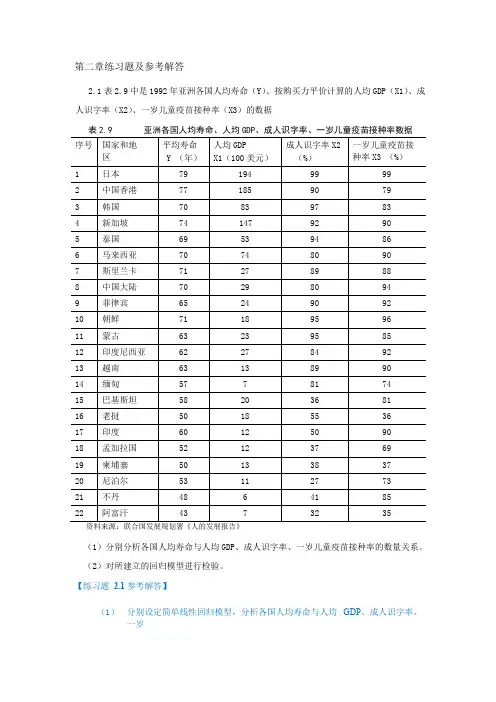
第二章练习题及参考解答2.1表2.9中是1992年亚洲各国人均寿命（Y）、按购买力平价计算的人均GDP（X1）、成人识字率（X2）、一岁儿童疫苗接种率（X3）的数据（1）分别分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系。

（2）对所建立的回归模型进行检验。

【练习题2.1 参考解答】（1）分别设定简单线性回归模型，分析各国人均寿命与人均GDP、成人识字率、一岁儿童疫苗接种率的数量关系:1)人均寿命与人均GDP 关系Y i 1 2 X1i u i估计检验结果:2)人均寿命与成人识字率关系3)人均寿命与一岁儿童疫苗接种率关系（2）对所建立的多个回归模型进行检验由人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命回归结果的参数t 检验值均明确大于其临界值,而且从对应的P 值看,均小于0.05,所以人均GDP、成人识字率、一岁儿童疫苗接种率分别对人均寿命都有显著影响.（3）分析对比各个简单线性回归模型人均寿命与人均GDP 回归的可决系数为0.5261 人均寿命与成人识字率回归的可决系数为0.7168 人均寿命与一岁儿童疫苗接种率的可决系数为0.5379相对说来,人均寿命由成人识字率作出解释的比重更大一些2.2为了研究浙江省财政预算收入与全省生产总值的关系,由浙江省统计年鉴得到以下数据:的显著性,用规范的形式写出估计检验结果,并解释所估计参数的经济意义(2)如果2011 年，全省生产总值为32000 亿元，比上年增长9.0%,利用计量经济模型对浙江省2011 年的财政预算收入做出点预测和区间预测(3)建立浙江省财政预算收入对数与全省生产总值对数的计量经济模型,. 估计模型的参数,检验模型的显著性,并解释所估计参数的经济意义【练习题2.2 参考解答】建议学生独立完成2.3 由12对观测值估计得消费函数为：（1）消费支出C的点预测值；（2）在95%的置信概率下消费支出C平均值的预测区间。

第一章导论第一节什么是计量经济学计量经济学是现代经济学的重要分支。

为了深入学习计量经济学的理论与方法，有必要首先从整体上对计量经济学有一些概略性的认识，了解计量经济学的性质、基本思想、基本研究方法以及若干常用的基本概念。

一、计量经济学的产生与发展在对实际经济问题的研究中，经常需要对经济活动及其数量变动规律作定量的分析。

例如，为了研究中国经济的增长，需要分析中国国内生产总值(GDP)变动的状况? 分析有哪些主要因素会影响中国GDP的增长？分析中国的GDP与各种主要影响因素关系的性质是什么？分析各种因素对中国GDP影响的程度和具体数量规律是什么？分析所得到的数量分析结果的可靠性如何？还要分析经济增长的政策效应，或者预测中国GDP发展的趋势。

显然，对这类经济问题的定量分析，需要解决一些共性问题：提出所研究的经济问题及度量方式，确定表现研究对象的经济变量（如用GDP的变动度量经济的增长）；分析对研究对象变动有影响的主要因素，选择若干作为影响因素的变量；分析各种影响因素与所研究经济现象相互关系的性质，决定相互联系的数学关系式；运用科学的数量分析方法，确定所研究的经济对象与各种影响因素间具体的数量规律；运用统计方法分析和检验所得数量结论的可靠性；运用数量研究的结果作经济分析和预测。

对社会经济问题数量规律的研究具有普遍性，计量经济学是专门研究这类问题的经济学科。

计量经济学（Econometrics）这个词是挪威经济学家、第一届诺贝尔经济学奖获得者弗瑞希（R.Frisch）在其1926年发表的《论纯经济问题》一文中，按照”生物计量学”(Biometrics)一词的结构仿造出来的。

Econometrics一词的本意是指“经济度量”，研究对经济现象和经济关系的计量方法，因此有时也译为“经济计量学”。

将Econometrics译为计量经济学，是为了强调计量经济学是一门经济学科，不仅要研究经济现象的计量方法，而且要研究经济现象发展变化的数量规律。

第三章考虑以下“期望扩充菲利普斯曲线（Expectations-augmented Phillips curve ）”模型：t t t t u X X Y +++=33221βββ其中：t Y =实际通货膨胀率（%）；t X 2=失业率（%）；t X 3=预期的通货膨胀率（%）表为某国的有关数据，表 1970-1982年某国实际通货膨胀率Y (%)，失业率X 2(%)和预期通货膨胀率X 3(%)1）对此模型作估计,并作出经济学和计量经济学的说明。

2）根据此模型所估计结果作统计检验。

3）计算修正的可决系数（写出详细计算过程）。

解答:（1）对此模型作估计,并作出经济学和计量经济学的说明。

（2）根据此模型所估计结果，作计量经济学的检验。

t 检验表明：各参数的t 值的绝对值均大于临界值0.025(133) 2.228t -=，从P 值也可看出均明显小于0.05α=，表明失业率和预期通货膨胀率分别对实际通货膨胀率都有显着影响。

F 检验表明： F=,大于临界值, 其P 值也明显小于0.05α=,说明失业率和预期通货膨胀率联合起来对实际通货膨胀率有显着影响。

从经济意义上看：失业率与实际通货膨胀率负相关，预期通货膨胀率与实际通货膨胀率正相关，与经济理论一致。

（3）计算修正可决系数（写出详细计算过程） 由Y 的统计量表得=214.12846ie=∑223.041892(131)111.0373iy=⨯-=∑214.12846110.12720.8728111.0373R =-=-=某市1974年—1987年粮食年销售量Y 、常住人口X2、人均收入X3、肉销售量X4、蛋销售量X5、鱼虾销售量X6等数据如表所示:表 某市粮食年销售量、常住人口、人均收入、肉、蛋、鱼虾销售量数据2211311(1)1(10.8728)0.8473133n R R n k --=--=--⨯=--1)建立线性回归模型：12233445566t t Y X X X X X u ββββββ=++++++，你预期所估计参数的符号应该是什么2）用OLS 法估计参数，模型参数估计的结果与你的预期是否相符合3）对模型及各个解释变量的显着性作检验,从检验结果中你能发现什么问题吗你如何评价这样的检验结果解答：1)建立线性回归模型：12233445566t t Y X X X X X u ββββββ=++++++ 预期常住人口和人均收入应与粮食销售量正相关，2β和3β应为正值，而肉、蛋、鱼虾与粮食消费应该负相关，预期4β、5β、6β应当为负值。

计量经济学复习重点总结任课老师：姜婷By fantasy题型：单选20*2 多选5*3 判断5*3 计算3*10第一章导论计量经济学数据类型：时间序列数据：把反映某一总体特征的同一指标的数据，按照一定的时间顺序和时间间隔（如月度.季度.年度）排列起来，这样的统计数据称为时间序列数据。

时间序列数据可以是时期数据，也可以是时点数据。

如逐年的GDP CPI截面数据：同一时间（时期或时点）某个指标在不同空间的观测数据。

如某一年各省GDP 面板数据：指时间序列数据和截面数据相结合的数据。

如在居民收支调查中收集的对各个固定调查户在不同时期的调查数据。

虚拟变量数据：某些客观存在的定性现象，如政策、自然灾害、战争等等第二章简单线性回归模型总体回归函数的表示形式：条件期望形式：个别值形式：样本回归函数的表示形式：条件均值形式个别值形式随机扰动项和残差项的区别和联系：区别：随机扰动项代表总体的误差，反应了未知因素、模型设定误差、变量观测误差；残差代表样本的误差，残差=随机误差项+参数估计误差。

随机扰动项无法直接观测；残差的数值可以求出。

联系：残差概念上类似于随机扰动项，将残差引入样本回归函数和随机引入总体回归函数的理由是相同的。

简单线性回归的基本假定：P31随机扰动项和解释变量不相关假定，零均值假定：同方差假定：正态性假定：无自相关假定：采用普通最小二乘法拟合的样本回归线的性质：P34回归线通过样本均值：Yi估计值的均值等于实际值的均值：剩余项的均值为零：被解释变量估计值与剩余项不相关：解释变量与剩余项不相关：OLS估计式的统计性质：P36（BLUE最佳线性无偏估计量）线性特性：无偏性：最小方差性：可决系数：R 2=ESS/TSS=1-RSS/TSS回归系数的假设检验：t 检验选取的统计量及其服从的分布 P48回归模型结果的经济含义分析： 练习题：2.7和2.92.7 设销售收入X 为解释变量，销售成本Y 为被解释变量。

第二章 简单线性回归模型第一节 回归分析与回归方程一、回归与相关 1、变量之间的关系（1）函数关系：()Y f X =，其中Y 为应变量，X 为自变量。

（2）相关关系或统计关系：当一个变量X 或若干个变量12,,,k X X X 变化时，Y 发生相应的变化（可能是不确定的），反之亦然。

在相关关系中，变量X 与变量Y 均为不确定的，并且它们之间的影响是双向的（双向因果关系）。

（3）单向因果关系：(,)Y f X u =，其中u 为随机变量。

在计量经济模型中，单一线性函数要求变量必须是单向因果关系。

在（单向）因果关系中，变量Y 是不确定的，变量X 是确定的（或可控制的）。

要注意的是，对因果关系的解释不是靠相关关系或统计关系来确定的，并且，相关关系与统计关系也给不出变量之间的具体数学形式，而是要通过其它相关理论来解释，如经济学理论。

例如，我们说消费支出依赖于实际收入是引用了消费理论的观点。

2、相关关系的类型 (1) 简单相关 (2) 复相关或多重相关 (3) 线性相关 (4) 非线性相关 (5) 正相关 (6) 负相关 (7) 不相关3、用图形法表示相关的类型上述相关类型可直观地用（EViews 软件）画图形来判断。

例如，美国个人可支配收入与个人消费支出之间的相关关系可由下列图形看出，它们为正相关关系。

15002000250030003500150020002500300035004000PDIP C E其中，PDI 为（美）个人可支配收入，PCE 为个人消费支出。

PDI 和PCE 分别对时间的折线图如下PROFIT 对STOCK 的散点图为05010015020025050100150STOCKP R O F I T其中，STOCK 为（美）公司股票利息，PROFIT 为公司税后利润，表现出明显的非线性特征。

以下是利润与股息分别对时间的序列图（或称趋势图）05010015020025020406080100120140GDP 对M2的散点图为02000040000600008000010000050000100000150000M2G D P其中M2为（中国）广义货币供应量，GDP 为国内生产总值。

第二章练习题参考解答练习题资料来源:《深圳统计年鉴2002》，中国统计出版社(1)建立深圳地方预算内财政收入对GDP的回归模型；(2)估计所建立模型的参数，解释斜率系数的经济意义；（3）对回归结果进行检验；(4)若是2005年年的国内生产总值为3600亿元，确定2005年财政收入的预测值和预测区间(0.05α=)。

2.2某企业研究与发展经费与利润的数据(单位:万元)列于下表:1995 1996 1997 1998 1999 2000 2001 2002 2003 2004研究与发展经费 10 10 8 8 8 12 12 12 11 11利润额 100 150 200 180 250 300 280 310 320 300 分析企业”研究与发展经费与利润额的相关关系，并作回归分析。

2.3为研究中国的货币供应量(以货币与准货币M2表示)与国内生产总值(GDP)的相互依存关系，分析表中1990年—2001年中国货币供应量（M2）和国内生产总值（GDP）的有关数据:年份货币供应量(亿元)M2国内生产总值(亿元)GDP1990 1529.31 8598.41991 19349.92 1662.51992 25402.22 6651.91993 34879.83 4560.51994 46923.54 6670.01995 60750.55 7494.91996 76094.96 6850.51997 90995.37 3142.71998 104498.57 6967.21999 119897.98 0579.42000 134610.38 8228.12001 158301.99 4346.4资料来源:《中国统计年鉴2002》，第51页、第662页，中国统计出版社对货币供应量与国内生产总值作相关分析，并说明分析结果的经济意义。

2.4表中是16支公益股票某年的每股帐面价值和当年红利：根据上表资料：（1）建立每股帐面价值和当年红利的回归方程；（2）解释回归系数的经济意义；（3）若序号为6的公司的股票每股帐面价值增加1元，估计当年红利可能为多少？2.5美国各航空公司业绩的统计数据公布在《华尔街日报1999年年鉴》（The Wall Street1。

1.计量分析的四个步骤：模型设定——参数估计——模型检验——模型应用2.计量模型检验：经济意义检验——统计推断检验——计量经济学检验——模型预测检验3.计量模型的应用：结构分析——经济预测——政策评价——检验与发展经济理论4.正确选择解释变量的原则：符合理论、规律——忽略众多次要因素，突出主要经济变量——数据可得性——每个解释变量之间是独立的5.参数的数据类型：时间序列数据——截面数据——面板数据——虚拟变量数据第二章1.总体相关系数：ρ=Cov(X,Y)/√Var(X)√Var(Y)2.样本相关系数：rxy=Σ(Xi-X_)(Yi-Y_)/√Σ(Xi-X_)^2√Σ(Yi-Y_)^23.总体回归函数中引入随机扰动项的原因：作为未知影响因素的代表——作为无法取得数据的已知因素代表——作为众多细小影响因素的综合代表——模型的设定误差——变量的观测误差——经济现象的内在随机性4.简单线性回归模型的基本假定：1、对变量和模型的假定；2、对随机扰动项ui统计分布的假定（古典假定）：零均值假定——同方差假定——无自相关假定——随机扰动项ui与解释变量Xi不相关——正态性假定5.违反零均值假定：影响截距上的估计（影响小）6.违反正态性假定：不影响OLS估计是最佳无偏性，但会使t检验F检验失真（影响大）7.样本回归函数的离差形式：yi^=β2^*xi8.OLS估计值的离差表达式：β2^=Σ(Xi-X_)(Yi-Y_)/Σ(Xi-X_)^2=Σxiyi/Σxi^2β1^=Y_-β2^*X_9.OLS回归线的性质：样本回归线过（X_,Y_）——估计值均值等于实际值均值——剩余项ei的均值为零——Cov(Yi^,ei)=0——Cov(Xi,ei)=010.β^的评价标准：无偏性——有效性——一致性11.β^的统计性质：线性——无偏性——有效性12.Var(^β1)=Ơ^2/Σxi^2——Var(^β2)=ΣXi^2/n*Ơ^2/Σxi^213.^Ơ^2=Σei^2/(n-2)14.总变差平方和：Σ(Yi-Y_)^2=Σyi^2……TSS……n-1回归平方和：Σ(Yi^-Y_)^2=Σ^yi^2……ESS……k-1残差平方和：Σ(Yi-Yi^)^2=Σei^2……RSS……n-k15.可决系数：R^2=ESS/TSS16.SE(^β1)=√(Ơ^2ΣXi^2)/(nΣxi^2)SE(^β2)=√Ơ^2/Σxi^217.t=(^β1-β1)/^SE(^β1)~t(n-2)t=(^β2-β2)/^SE(^β2)~t(n-2)18.区间估计：1.当总体方差Ơ^2已知，α=0.1—±1.645, α=0.05—±1.96, α=0.01—±2.33，P[-tα<z=(^β2-β2)/^SE(^β2)<tα]=1-α2.当总体方差Ơ^2未知，样本容量大，可用^Ơ^2=Σei^2/(n-2)代替Ơ^2，z=(^β2-β2)/(^Ơ/√Σxi^2)3.当总体方差Ơ^2未知，样本容量小，P[-tα/2< t=(^β2-β2)/^SE(^β2)<tα/2]=1-α19.对Y平均值的区间预测：SE(^Yf)=Ơ√{1/n+[(Xf-X_)^2/Σxi^2]}，置信度1-α的预测区间[^Yf-tα/2* SE(^Yf), ^Yf+tα/2* SE(^Yf)]20.对Y个别值预测区间：Yf=^Yf±tα/2*^Ơ√{1+1/n+[(Xf-X_)^2/Σxi^2]}1.多元线性回归模型的古典假定：零均值假定——同方差和无自相关假定——随机扰动项与解释变量不相关——无多重共线性假定——正态性假定2.修正的可决系数：_R^2=1-(1-R^2)(n-1)/(n-k)……k是待估参数个数，R^2必定为正，但修正的可决系数可能为负，这是规定其为0，随着k的增加，_R^2越来越小于R^23.F=ESS(k-1)/RSS(n-k)=R^2/(1-R^2)*(n-k)/(k-1)4.S.E. of regression：Ơ^2=Σei^2/(n-k)——Ơ=5.t-statistic=coefficient/std.error6.TSS=(n-1)*(S.D.dependent var)^2第四章1.多重共线性产生的原因：经济变量之间具有共同变化趋势——模型中包含滞后变量——利用截面数据建立模型也可能出现多重共线性——样本数据自身的原因2.完全多重共线性产生的后果：参数的估计值不确定——参数估计值得方差无限大3.不完全多重共线性后果：参数估计值的方差和协方差增大——对参数区间估计时，置信区间趋于变大——严重多重共线性时，假设检验容易作出错误判断——参数估计经济含义不合理。

计量经济学实验简单线性回归模型引言计量经济学是经济学中的一个分支，致力于通过经验分析和实证方法来研究经济问题。

实验是计量经济学中的重要方法之一，能够帮助我们理解和解释经济现象。

简单线性回归模型是实验中常用的工具之一，它能够通过建立两个变量之间的数学关系，预测一个变量对另一个变量的影响。

本文将介绍计量经济学实验中的简单线性回归模型及其应用。

简单线性回归模型模型定义简单线性回归模型是一种用于描述自变量（X）与因变量（Y）之间关系的线性模型。

其数学表达式为：Y = β0 + β1X + ε其中，Y表示因变量，X表示自变量，β0和β1为未知参数，ε表示误差项。

参数估计在实际应用中，我们需要通过数据来估计模型中的参数。

最常用的估计方法是最小二乘法（OLS）。

最小二乘法的目标是通过最小化观测值与拟合值之间的平方差来估计参数。

具体而言，我们需要求解以下两个方程来得到参数的估计值：∂(Y - β0 - β1X)^2 / ∂β0 = 0∂(Y - β0 - β1X)^2 / ∂β1 = 0解释变量与被解释变量在简单线性回归模型中，解释变量（X）用来解释或预测被解释变量（Y）。

例如，我们可以使用房屋的面积（X）来预测房屋的价格（Y）。

在实验中，我们可以根据收集到的数据来建立回归模型，并利用该模型进行预测和分析。

应用实例数据收集为了说明简单线性回归模型的应用，我们假设收集了一些关于学生学习时间与考试成绩的数据。

下面是收集到的数据：学习时间（小时）考试成绩（百分制）2 723 784 805 856 88模型建立根据收集到的数据，我们可以建立简单线性回归模型来分析学生学习时间与考试成绩之间的关系。

首先，我们需要确定自变量和因变量的符号。

在这个例子中，我们可以将学习时间作为自变量（X），考试成绩作为因变量（Y）。

然后，我们使用最小二乘法来估计模型中的参数。

通过计算，可以得到如下参数估计值：β0 = 69.85β1 = 2.95最终的回归方程为：Y = 69.85 + 2.95X预测与分析通过建立的回归模型，我们可以进行预测和分析。