计量经济学庞皓课件(第三章 多元线性回归模型)
- 格式:pptx
- 大小:1.18 MB
- 文档页数:55





第三章多元线性回归模型案例分析一、研究目的1提出问题:研究中国税收收入增长的主要原因(必须要有研究的意义,且具创新价值)2分析问题:从宏观经济看经济增长是税收增长的源泉;公共财政的需求;物价水平;税收政策(要注重经济理论的相关性和逻辑性)二、模型设定1被解释变量:为了全面反映中国税收增长的全貌,选择包括中央和地方的的“国家财政收入”中的各项税收作为被解释变量2解释变量:选择“国内生产总值GDP”作为经济整体增长水平的代表;选择中央和地方“财政支出”作为公共财政需求的代表,选择“商品零售物价指数”作为物价水平的代表,而由于财政体制的改革难以量化,且1985年后财税体制改革对税收增长影响不是很大,故暂不考虑。
3设定线性模型为:Y t= β1+β2X2t+β3 X3t+β4 X4t +u t注:X1默认为14经济理论构造成功之后,即着手收集数据资料(这要借助统计学的知识进行整理,并不是什么数据都可以直接拿来用。
首先,数据来源的权威性,即必须保证数据的准确可靠性,不能随意捏造,其次,数据的合理分类,最后是数据的合理运用)附:数据三、估计参数利用eviews3.0进行分析1建立工作文件新建工作文档:file-new-workfile,在打开的workfile range 对话框中的workfile frequency 中选择annual,start date 输入1978,end date输入2002,点击ok。
2输入数据直接在命令窗口输入“data Y X2 X3 X4 、、、”本案例中输入data Y X2 X3 X4然后是将excel中的数据复制过来,并点击name命名GROUP01。
3估计参数直接在命令窗口输入“LS Y C X2 X3 X4 、、、”。
LS是做最小二乘估计的命令,Y为被解释变量,C为截距项,X为解释变量,注意LS Y C X之间要有空格,被解释变量紧接在命令LS之后。
本案例中输入LS Y C X2 X3 X4 本题中得到下表,点击name 命名eq01。

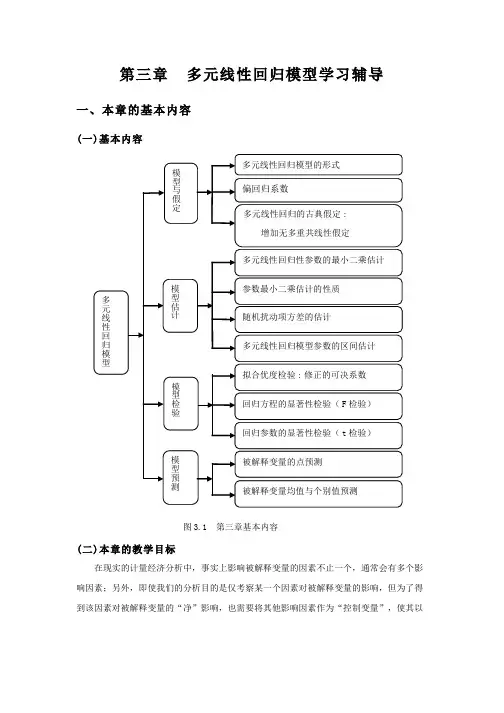
第三章 多元线性回归模型学习辅导一、本章的基本内容(一)基本内容图3.1 第三章基本内容(二)本章的教学目标在现实的计量经济分析中,事实上影响被解释变量的因素不止一个,通常会有多个影响因素;另外,即使我们的分析目的是仅考察某一个因素对被解释变量的影响,但为了得到该因素对被解释变量的“净”影响,也需要将其他影响因素作为“控制变量”,使其以显性形式出现在模型中,以提高模型估计精度。
因此,在对现实经济问题进行计量经济分析时,通常需要建立包含两个及两个以上解释变量的计量模型,此类模型称为多元回归模型。
多元回归模型是在简单回归模型理论基础上的扩展,其建模的理论基础、基本思路、模型估计等与一元回归模型基本一致,只是因解释变量增多,从而带来一些新的内容,比如模型整体显著性检验(F 检验)、修正的可决系数(2R )以及解释变量之间多重共线性等问题。
本章的教学目标是:深刻理解建立多元回归模型的目的;掌握多元线性回归模型估计、检验的理论与方法;熟练掌握多元线性回归EViews 输出结果的解释。
二、重点与难点分析1.对多元线性回归模型参数意义的理解多元线性回归模型的参数与简单线性回归模型的参数有重要区别。
在多元线性回归模型中,解释变量对应的参数是偏回归系数,表达的是控制其他解释变量不变的条件下,该解释变量的单位变动对被解释变量平均值的“净”影响。
为了更深刻理解偏回归系数,可以两个解释变量的多元线性回归模型为例加以说明1。
例如,被解释变量Y 与解释变量2X 和3X 都有关,如果分别建立模型:多元线性回归: 12233i i i i Y X X u b b b =+++简单线性回归 : 1221i i i Y a a X u =++由于Y 与3X 有关,可以作回归:1332i i i Y b b X u =++,若用OLS 估计其参数,并计算残差213333ˆˆˆi i i i i e Y b b X y b x =--=-,这里的2i e 表示除去3i X 影响后的i Y 。




第三章 多元线性回归模型第一节 多元线性回归模型及基本假定问题:只有一个解释变量的线性回归模型能否满足分析经济问题的需要?简单线性回归模型的主要缺陷是:把被解释变量Y 看成是解释变量X 的函数是前提是,在其它条件不变的情况下,并且,所有其它影响Y 的因素都应与X 不相关,但这在实际情况中很难满足。
怎样在一元线性回归的基础上引入多元变量的回归? 看教科书第72—73页关于汽车销售量的影响因素的讨论。
一、多元线性回归模型的意义1、建立多元线性回归模型的意义,即一元线性回归模型的缺陷,多个主要影响因素的缺失对模型的不利影响。
在一元线性回归模型中,如果总体回归函数的设定是正确的,那么,根据样本数据得到的样本回归模型就应该有较好的拟合效果,这时,可决系数就应该较大。
相反,如果在模型设定时忽略了影响被解释变量的某些重要因素,拟合效果可能就会较差,此时可决系数会偏低,并且由于忽略了一些重要变量而对误差项的影响会加大,这时误差项会表现出一些违背假定的情况。
2、从一个解释变量到多个解释变量的演变。
一个生产函数的例子,一个商品需求函数的例子,(教材第74页)。
二、多元线性回归模型及其矩阵表示1、一般线性回归模型的数学表达式。
设 12233i ii k k ii Y XXXu ββββ=+++++i=1,2,3,…,n在模型表达式里,1β仍是截距项,它反映的是当所有解释变量取值为零时,被解释变量Y 的取值;j β(j=2,3,…,k )为斜率系数,它的经济含义:在其它变量不变的情况下,第j 个解释变量每变动一个单位,Y 平均增加(或减少)j β个单位,这就是所谓的运用边际分析法对多元变量意义下回归参数的解释。
因此,称j β为偏回归系数,它反映了第j 个解释变量对Y 的边际影响程度。
4、2、总体回归函数,即12233(|)i i i k ki E Y X X X X ββββ=++++3、样本回归函数,即12233ˆˆˆˆˆi i k k iY X X Xββββ=++++ 4、将n 个样本观测值代入上述表达式,可得到从形式上看,像似方程组的形式。